八年级上册沪科版数学第14章 全等三角形 测试卷(含答案)
文档属性
| 名称 | 八年级上册沪科版数学第14章 全等三角形 测试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-21 19:44:48 | ||
图片预览



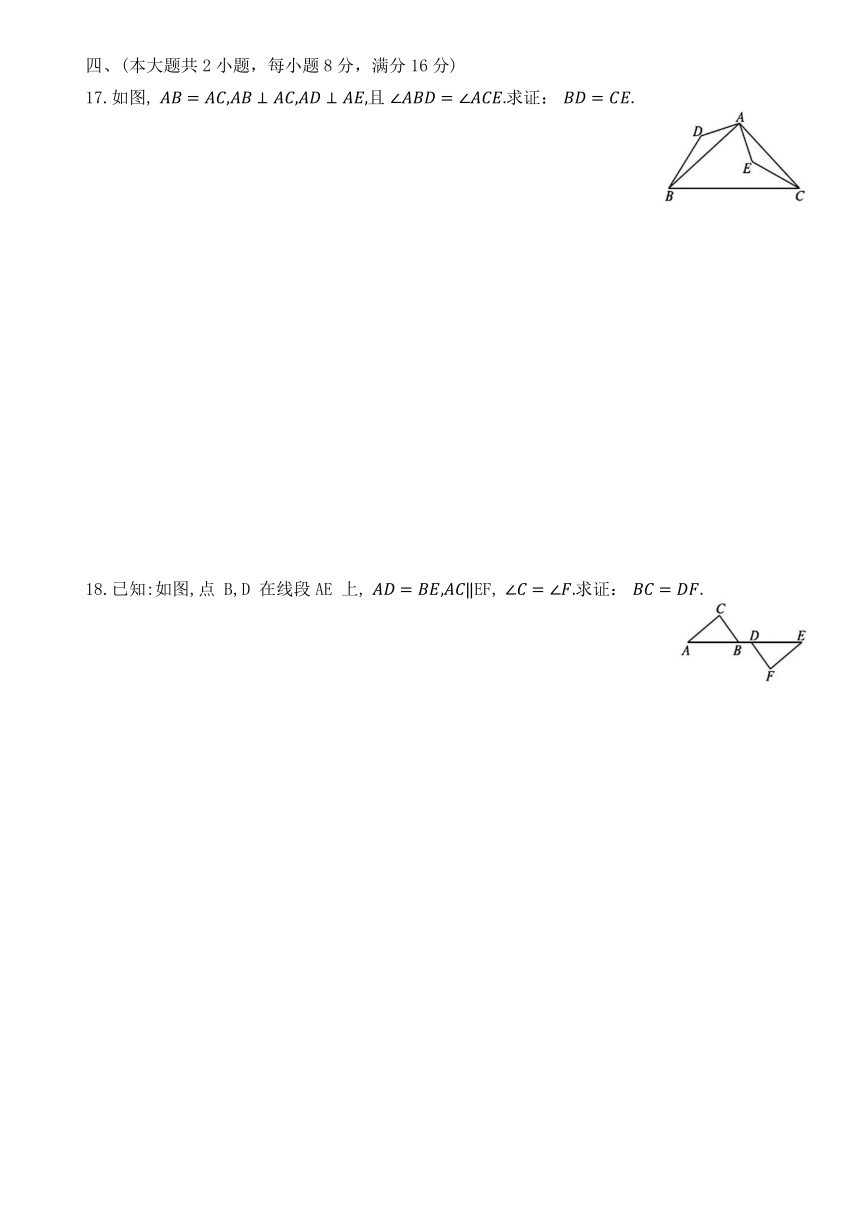
文档简介
第 14 章测试卷
(时间:120分钟 满分:150分)
题号 一 二 三 四 五 六 七 八 总分
得分
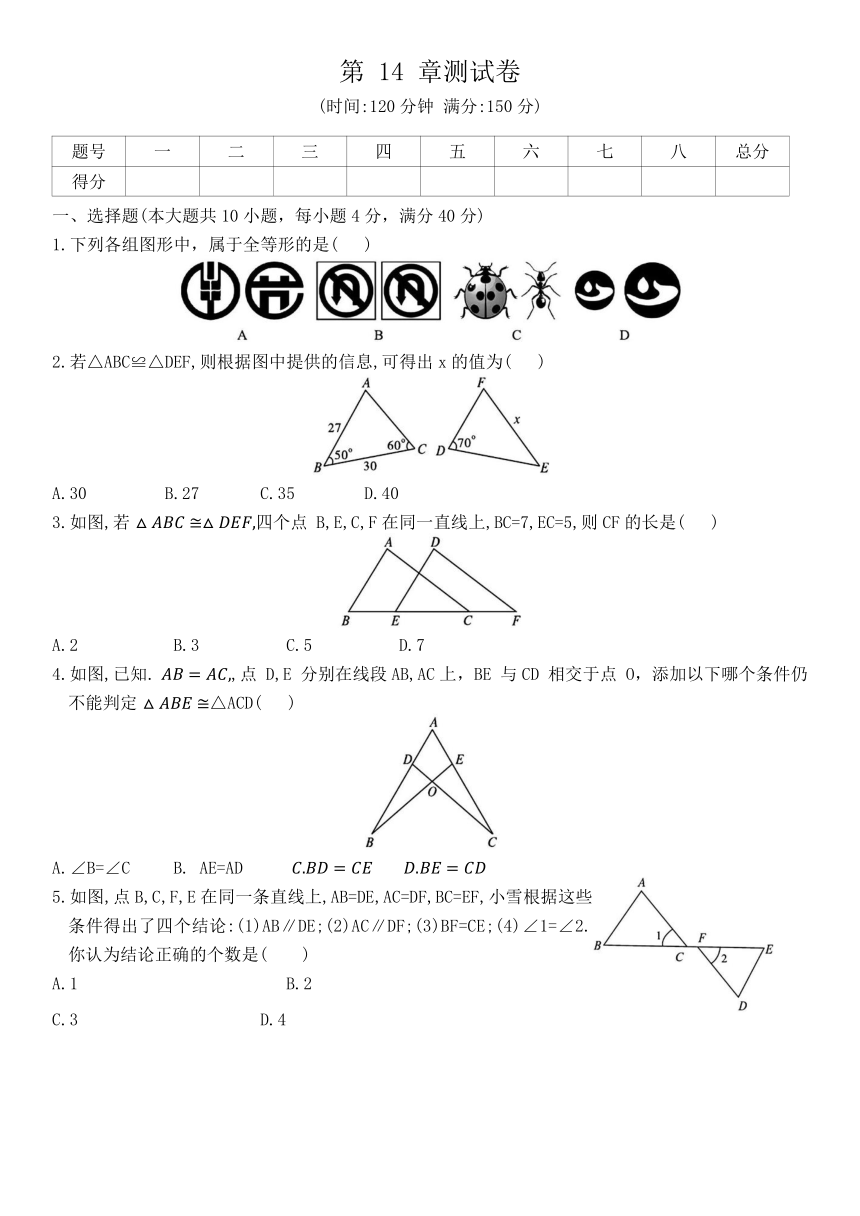
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列各组图形中,属于全等形的是( )
2.若△ABC≌△DEF,则根据图中提供的信息,可得出x的值为( )
A.30 B.27 C.35 D.40
3.如图,若 四个点 B,E,C,F在同一直线上,BC=7,EC=5,则CF的长是( )
A.2 B.3 C.5 D.7
4.如图,已知. ,点 D,E 分别在线段AB,AC上,BE 与CD 相交于点 O,添加以下哪个条件仍不能判定 △ACD( )
A.∠B=∠C B. AE=AD
5.如图,点B,C,F,E在同一条直线上,AB=DE,AC=DF,BC=EF,小雪根据这些条件得出了四个结论:(1)AB∥DE;(2)AC∥DF;(3)BF=CE;(4)∠1=∠2.你认为结论正确的个数是( )
A.1 B.2
C.3 D.4
6.如图,工人师傅加工了一个长方形窗框ABCD,E,F,G,H 分别是四条边的中点,为使它稳固,需要钉一根木条,这根木条不应钉在( )
A. A,C两点 B. E,G两点
C. B,F两点 D. G,H两点
7.如图,在 中, 垂足分别为D,E,AD,CE交于点H,已知. 4,则CH的长是( )
A.4 B.3
C.2 D.1
8.如图所示的是 正方形网格, 等于( ).
9.数学活动课上,小敏、小颖分别画了 和△DEF,尺寸如图所示.如果把小敏画的三角形的面积记作S△ABC,小颖画的三角形的面积记作S△DEF,那么你认为( )
C. S△ABC>S△DEF D.不能确定
10.如图,在△OAB 和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;② ③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为( )
A.4 B.3 C.2 D.1
二、填空题(本大题共4小题,每小题5分,满分20分)
11.空调安装在墙上时,一般都会采用如图所示的方法固定,这种方法应用的几何原理是
12.如图,用直尺和圆规作一个角等于已知角的示意图如下,则说明 的依据是 .
13.如图,已知 添加下列条件中的一个: DB,③AB=DC,其中不能确定. 的是 (只填序号).
14.如图,E是BC 边上一点, 于点B,CD⊥CB于点C, AE 与 BD相交于点O,下列结论:①AE=BD;②AE⊥BD;③EB=CD;④△ABO的面积等于四边形CDOE的面积.其中正确的结论有 (填序号).
三、(本大题共2小题,每小题8分,满分16分)
15.如图,在左侧标有字母的六个图形中,其中有五个分别与右侧标有数字的图形全等,请找出它们.
16.如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点 C,从点 C不经过池塘可以直接到达点A 和B.连接AC 并延长到点D,使 连接BC并延长到点E,使 连接DE,那么量出 DE的长就是A,B 的距离.为什么
四、(本大题共2小题,每小题8分,满分16分)
17.如图, 且 求证:
18.已知:如图,点 B,D 在线段AE 上, EF, 求证:
五、(本大题共2 小题,每小题10分,满分20分)
19.如图,点 E,A,C在同一直线上,AB∥CD,AB=CE,AC=CD.求证:BC=ED.
20.如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE 的中点,过点 E作EF⊥AE,过点A作AF∥BC,且AF,EF相交于点F.
(1)求证:∠C=∠BAD;
(2)求证:AC=EF.
六、(本题满分12分)
21.如图,在△ABC中,D 是BC 边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.
(1)求证:△ABE≌△DBE;
(2)若∠A=100°,∠C=50°,求∠AEB的度数.
22.已知,在 中, 点 D 为 BC的中点.
(1)如图①,若点 E,F分别为AB,AC 上的点,且 求证:
(2)若点 E,F分别为AB,CA 延长线上的点,且. ,那么 AF吗 请利用图②说明理由.
八、(本题满分14分)
23.(1)如图①,在四边形ABCD 中, 点 E 是BC 的中点,若AE 是 的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE 交DC 的延长线于点 F,易证 得到 ,从而把AB,AD,DC转化在一个三角形中即可判断.
(1)AB,AD,DC之间的等量关系 ;
(2)问题探究:如图②,在四边形ABCD中, AF 与DC 的延长线交于点 F,点 E 是BC 的中点,若AE 是 的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
第 14 章测试卷
1. B 2. A 3. A 4. D 5. D 6. B 7. D 8. C 9. A10. B
11.三角形具有稳定性 12. SSS 13.② 14.①②③④
15.解a与2,b与3,c与4,d与5,e与6.
16.解 量出 DE的长就等于AB 的长,理由如下:
在△ABC和△DEC中,
∴△ABC≌△DEC(SAS),∴AB=DE.
17.证明∵AB⊥AC,AD⊥AE,
∴∠BAE+∠CAE=90°,∠BAE+∠BAD=90°,
∴∠CAE=∠BAD.
又∵AB=AC,∠ABD=∠ACE,∴△ABD≌△ACE(ASA).∴BD=CE.
18.证明∵AD=BE,∴AD--BD=BE--BD,∴AB=ED,∵AC∥EF,∴∠A=∠E,
在△ABC和△EDF中,
∴△ABC≌△EDF(AAS),∴BC=DF.
19.证明∵AB∥CD,∴∠BAC=∠ECD.在△ABC和△CED中,
∴△ABC≌△CED(SAS),∴BC=ED.
20.证明(1)∵AB=AE,D为线段BE的中点,∴AD⊥BC,∴∠C+∠DAC=90°,∵∠BAC=90°,∴∠BAD +∠DAC=90°.∴∠C=∠BAD.
(2)∵AF∥BC,∴∠FAE=∠AEB,
∵AB=AE,∴∠B=∠AEB,
∴∠B=∠FAE,且∠AEF=∠BAC=90°,AB=AE,
∴△ABC≌△EAF(ASA),∴AC=EF.
21.(1)证明∵BE平分∠ABC,∴∠ABE=∠DBE,在△ABE 和△DBE中,
△DBE(SAS).
(2)解∵∠A=100°,∠C=50°,∴∠ABC=30°,∵BE平分 在△ABE中,∠AEB=180°-∠A-∠ABE=180°-100°-15°=65°.
22.(1)证明 如图①,连接AD,∵∠BDA=∠EDF=90°,
∴∠BDE+∠EDA=∠EDA+∠ADF.
∴∠BDE=∠ADF.又∵D为BC的中点,△ABC是等腰直角三角形,∴BD=AD,∠B=∠DAC=45°.
∴△BDE≌△ADF(ASA).∴BE=AF.
(2)解 如图②,连接AD,∵∠BDA=∠EDF=90°,
∴∠BDE+∠BDF=∠BDF+∠ADF.
∴∠BDE=∠ADF.又∵D为BC的中点,△ABC是等腰直角三角形,∴BD=AD,∠ABC=∠DAC=45°.
∴∠EBD=∠FAD=180°-45°=135°.
∴△BDE≌△ADF(ASA).∴BE=AF.
23.解(1)AD=AB+DC
理由如下:∵AE 是∠BAD 的平分线,∴∠DAE=∠BAE,
∵AB∥CD,∴∠F=∠BAE,∴∠DAF=∠F,∴AD=DF,
∵点 E 是 BC 的中点,∴CE=BE,且∠F=∠BAE,∠AEB=∠CEF,
∴△CEF≌△BEA(AAS),∴AB=CF,
∴AD=CD+CF=CD+AB.
(2)AB=AF+CF.
理由如下:如图②,延长AE交DF的延长线于点G.
∵E是BC的中点,∴CE=BE,
∵AB∥DC,∴∠BAE=∠G,且BE=CE,∠AEB=∠GEC,
∴△AEB≌△GEC(AAS),∴AB=GC,
∵AE 是∠BAF的平分线,∴∠BAG=∠FAG,
∵∠BAG=∠G,∴∠FAG=∠G,∴FA=FG,
(时间:120分钟 满分:150分)
题号 一 二 三 四 五 六 七 八 总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列各组图形中,属于全等形的是( )
2.若△ABC≌△DEF,则根据图中提供的信息,可得出x的值为( )
A.30 B.27 C.35 D.40
3.如图,若 四个点 B,E,C,F在同一直线上,BC=7,EC=5,则CF的长是( )
A.2 B.3 C.5 D.7
4.如图,已知. ,点 D,E 分别在线段AB,AC上,BE 与CD 相交于点 O,添加以下哪个条件仍不能判定 △ACD( )
A.∠B=∠C B. AE=AD
5.如图,点B,C,F,E在同一条直线上,AB=DE,AC=DF,BC=EF,小雪根据这些条件得出了四个结论:(1)AB∥DE;(2)AC∥DF;(3)BF=CE;(4)∠1=∠2.你认为结论正确的个数是( )
A.1 B.2
C.3 D.4
6.如图,工人师傅加工了一个长方形窗框ABCD,E,F,G,H 分别是四条边的中点,为使它稳固,需要钉一根木条,这根木条不应钉在( )
A. A,C两点 B. E,G两点
C. B,F两点 D. G,H两点
7.如图,在 中, 垂足分别为D,E,AD,CE交于点H,已知. 4,则CH的长是( )
A.4 B.3
C.2 D.1
8.如图所示的是 正方形网格, 等于( ).
9.数学活动课上,小敏、小颖分别画了 和△DEF,尺寸如图所示.如果把小敏画的三角形的面积记作S△ABC,小颖画的三角形的面积记作S△DEF,那么你认为( )
C. S△ABC>S△DEF D.不能确定
10.如图,在△OAB 和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;② ③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为( )
A.4 B.3 C.2 D.1
二、填空题(本大题共4小题,每小题5分,满分20分)
11.空调安装在墙上时,一般都会采用如图所示的方法固定,这种方法应用的几何原理是
12.如图,用直尺和圆规作一个角等于已知角的示意图如下,则说明 的依据是 .
13.如图,已知 添加下列条件中的一个: DB,③AB=DC,其中不能确定. 的是 (只填序号).
14.如图,E是BC 边上一点, 于点B,CD⊥CB于点C, AE 与 BD相交于点O,下列结论:①AE=BD;②AE⊥BD;③EB=CD;④△ABO的面积等于四边形CDOE的面积.其中正确的结论有 (填序号).
三、(本大题共2小题,每小题8分,满分16分)
15.如图,在左侧标有字母的六个图形中,其中有五个分别与右侧标有数字的图形全等,请找出它们.
16.如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点 C,从点 C不经过池塘可以直接到达点A 和B.连接AC 并延长到点D,使 连接BC并延长到点E,使 连接DE,那么量出 DE的长就是A,B 的距离.为什么
四、(本大题共2小题,每小题8分,满分16分)
17.如图, 且 求证:
18.已知:如图,点 B,D 在线段AE 上, EF, 求证:
五、(本大题共2 小题,每小题10分,满分20分)
19.如图,点 E,A,C在同一直线上,AB∥CD,AB=CE,AC=CD.求证:BC=ED.
20.如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE 的中点,过点 E作EF⊥AE,过点A作AF∥BC,且AF,EF相交于点F.
(1)求证:∠C=∠BAD;
(2)求证:AC=EF.
六、(本题满分12分)
21.如图,在△ABC中,D 是BC 边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.
(1)求证:△ABE≌△DBE;
(2)若∠A=100°,∠C=50°,求∠AEB的度数.
22.已知,在 中, 点 D 为 BC的中点.
(1)如图①,若点 E,F分别为AB,AC 上的点,且 求证:
(2)若点 E,F分别为AB,CA 延长线上的点,且. ,那么 AF吗 请利用图②说明理由.
八、(本题满分14分)
23.(1)如图①,在四边形ABCD 中, 点 E 是BC 的中点,若AE 是 的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE 交DC 的延长线于点 F,易证 得到 ,从而把AB,AD,DC转化在一个三角形中即可判断.
(1)AB,AD,DC之间的等量关系 ;
(2)问题探究:如图②,在四边形ABCD中, AF 与DC 的延长线交于点 F,点 E 是BC 的中点,若AE 是 的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
第 14 章测试卷
1. B 2. A 3. A 4. D 5. D 6. B 7. D 8. C 9. A10. B
11.三角形具有稳定性 12. SSS 13.② 14.①②③④
15.解a与2,b与3,c与4,d与5,e与6.
16.解 量出 DE的长就等于AB 的长,理由如下:
在△ABC和△DEC中,
∴△ABC≌△DEC(SAS),∴AB=DE.
17.证明∵AB⊥AC,AD⊥AE,
∴∠BAE+∠CAE=90°,∠BAE+∠BAD=90°,
∴∠CAE=∠BAD.
又∵AB=AC,∠ABD=∠ACE,∴△ABD≌△ACE(ASA).∴BD=CE.
18.证明∵AD=BE,∴AD--BD=BE--BD,∴AB=ED,∵AC∥EF,∴∠A=∠E,
在△ABC和△EDF中,
∴△ABC≌△EDF(AAS),∴BC=DF.
19.证明∵AB∥CD,∴∠BAC=∠ECD.在△ABC和△CED中,
∴△ABC≌△CED(SAS),∴BC=ED.
20.证明(1)∵AB=AE,D为线段BE的中点,∴AD⊥BC,∴∠C+∠DAC=90°,∵∠BAC=90°,∴∠BAD +∠DAC=90°.∴∠C=∠BAD.
(2)∵AF∥BC,∴∠FAE=∠AEB,
∵AB=AE,∴∠B=∠AEB,
∴∠B=∠FAE,且∠AEF=∠BAC=90°,AB=AE,
∴△ABC≌△EAF(ASA),∴AC=EF.
21.(1)证明∵BE平分∠ABC,∴∠ABE=∠DBE,在△ABE 和△DBE中,
△DBE(SAS).
(2)解∵∠A=100°,∠C=50°,∴∠ABC=30°,∵BE平分 在△ABE中,∠AEB=180°-∠A-∠ABE=180°-100°-15°=65°.
22.(1)证明 如图①,连接AD,∵∠BDA=∠EDF=90°,
∴∠BDE+∠EDA=∠EDA+∠ADF.
∴∠BDE=∠ADF.又∵D为BC的中点,△ABC是等腰直角三角形,∴BD=AD,∠B=∠DAC=45°.
∴△BDE≌△ADF(ASA).∴BE=AF.
(2)解 如图②,连接AD,∵∠BDA=∠EDF=90°,
∴∠BDE+∠BDF=∠BDF+∠ADF.
∴∠BDE=∠ADF.又∵D为BC的中点,△ABC是等腰直角三角形,∴BD=AD,∠ABC=∠DAC=45°.
∴∠EBD=∠FAD=180°-45°=135°.
∴△BDE≌△ADF(ASA).∴BE=AF.
23.解(1)AD=AB+DC
理由如下:∵AE 是∠BAD 的平分线,∴∠DAE=∠BAE,
∵AB∥CD,∴∠F=∠BAE,∴∠DAF=∠F,∴AD=DF,
∵点 E 是 BC 的中点,∴CE=BE,且∠F=∠BAE,∠AEB=∠CEF,
∴△CEF≌△BEA(AAS),∴AB=CF,
∴AD=CD+CF=CD+AB.
(2)AB=AF+CF.
理由如下:如图②,延长AE交DF的延长线于点G.
∵E是BC的中点,∴CE=BE,
∵AB∥DC,∴∠BAE=∠G,且BE=CE,∠AEB=∠GEC,
∴△AEB≌△GEC(AAS),∴AB=GC,
∵AE 是∠BAF的平分线,∴∠BAG=∠FAG,
∵∠BAG=∠G,∴∠FAG=∠G,∴FA=FG,
