第一章 丰富的图形世界 1 生活中的立体图形 第1课时 几何体与棱柱(含答案)
文档属性
| 名称 | 第一章 丰富的图形世界 1 生活中的立体图形 第1课时 几何体与棱柱(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-21 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第一章 丰富的图形世界
1 生活中的立体图形
第1课时 几何体与棱柱
基础闯关
知识点一:几何体的认识及分类
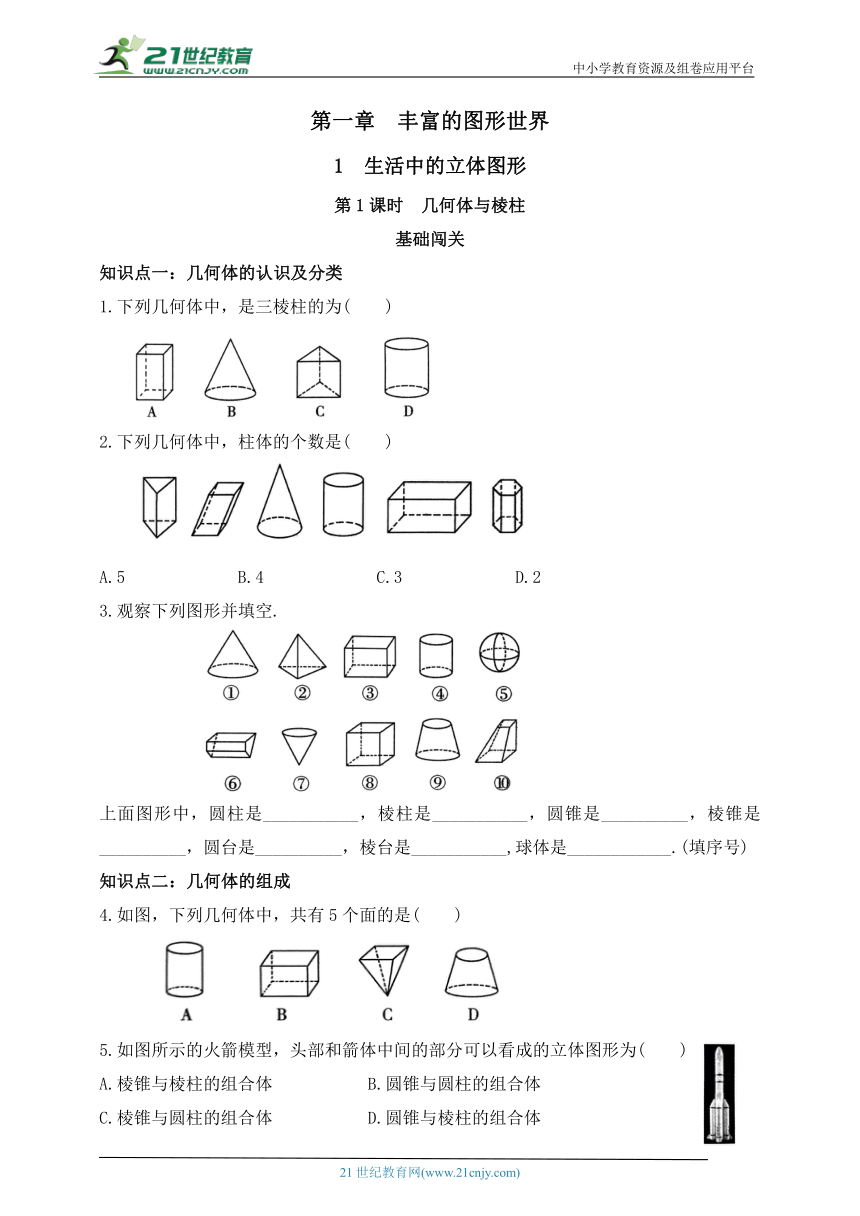
1.下列几何体中,是三棱柱的为( )
2.下列几何体中,柱体的个数是( )
A.5 B.4 C.3 D.2
3.观察下列图形并填空.
上面图形中,圆柱是___________,棱柱是___________,圆锥是__________,棱锥是__________,圆台是__________,棱台是___________,球体是____________.(填序号)
知识点二:几何体的组成
4.如图,下列几何体中,共有5个面的是( )
5.如图所示的火箭模型,头部和箭体中间的部分可以看成的立体图形为( )
A.棱锥与棱柱的组合体 B.圆锥与圆柱的组合体
C.棱锥与圆柱的组合体 D.圆锥与棱柱的组合体
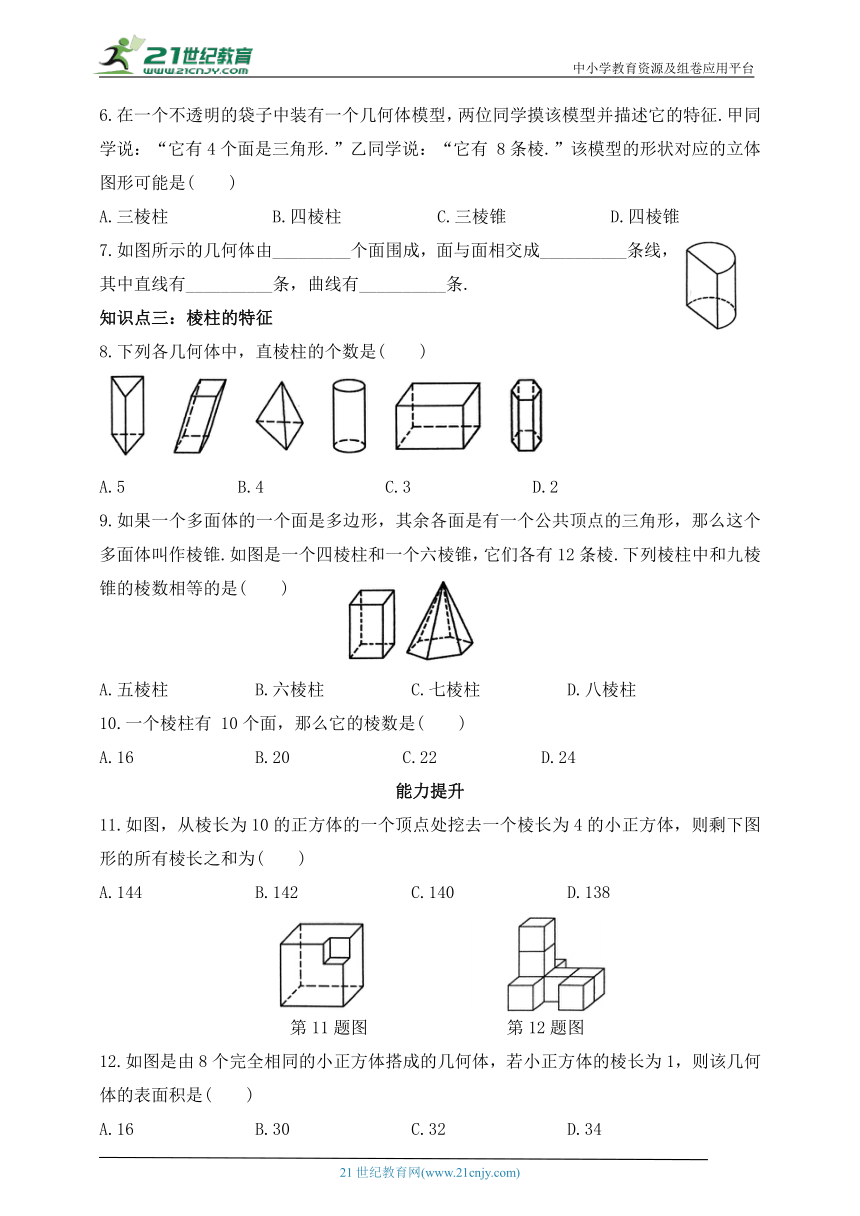
6.在一个不透明的袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征.甲同学说:“它有4个面是三角形.”乙同学说:“它有 8条棱.”该模型的形状对应的立体图形可能是( )
A.三棱柱 B.四棱柱 C.三棱锥 D.四棱锥
7.如图所示的几何体由_________个面围成,面与面相交成__________条线,其中直线有__________条,曲线有__________条.
知识点三:棱柱的特征
8.下列各几何体中,直棱柱的个数是( )
A.5 B.4 C.3 D.2
9.如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫作棱锥.如图是一个四棱柱和一个六棱锥,它们各有12条棱.下列棱柱中和九棱锥的棱数相等的是( )
A.五棱柱 B.六棱柱 C.七棱柱 D.八棱柱
10.一个棱柱有 10个面,那么它的棱数是( )
A.16 B.20 C.22 D.24
能力提升
11.如图,从棱长为10的正方体的一个顶点处挖去一个棱长为4的小正方体,则剩下图形的所有棱长之和为( )
A.144 B.142 C.140 D.138
第11题图 第12题图
12.如图是由8个完全相同的小正方体搭成的几何体,若小正方体的棱长为1,则该几何体的表面积是( )
A.16 B.30 C.32 D.34
13.如图,模块①由15个棱长为1的小正方体构成,模块②~⑥均由4个棱长为1的小正方体构成.现在从模块②~⑥中选出三个模块放到模块①上,与模块①组成一个棱长为3的大正方体.下列四个方案中,符合上述要求的是( )
A.模块②④⑤ B.模块③④⑥ C.模块②③⑥ D.模块③⑤⑥
14.如图,一个圆柱形钢化玻璃容器的底面半径是 10cm,把一块浸没于水中的铁块从这个容器中取出后,水面下降2cm,则这块铁块的体积是_______cm .(铁块带出的水忽略不计)
15.如图是一个底面各边都相等的六棱柱,它的底面边长为 2cm,高为5cm.这个棱柱共有________条棱,________个面,侧面积是________cm .
第15题图 第16题图
16.(1)如图,补全图形,使之成为完整的长方体
(2)已知这个长方体的长、宽、高的比是6:5:3,长方体的棱长总和为168,则这个长
方体的长=_________,宽=________,高=_________.
17.如图所示的四个几何体分别是三棱柱、四棱柱、五棱柱和六棱柱,三棱柱有 5个面,9 条棱,6个顶点,观察图形,完成下面各题.
(1)四棱柱有________个面,________条棱,_______个顶点.
(2)五棱柱有________个面,________条棱,_______个顶点.
(3)由此猜想:n 棱柱有_______个面,_______条棱,________个顶点.
培优创新
18.如图是由若干个小三棱锥堆成的一个大三棱锥,把大三棱锥的四个面都涂上颜色.若把其中1个面涂色的小三棱锥叫中心块,2个面涂色的叫棱块,3个面涂色的叫角块,则“(中心块数)一(棱块数)一(角块数)”得( )
A.0 B.2 C.4 D.6
参考答案
1. C 2. A
3.④ ③⑥⑧ ①⑦ ② ⑨ ⑩ ⑤
4. C 5. B 6. D
7.4 6 4 2
8. C 9. B 10. D 11. A 12. D 13. C
14.200π
15.18 8 60
16.解:(1)图略. (2)18 15 9
17.(1)6 12 8 (2)7 15 10 (3)
18. B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一章 丰富的图形世界
1 生活中的立体图形
第1课时 几何体与棱柱
基础闯关
知识点一:几何体的认识及分类
1.下列几何体中,是三棱柱的为( )
2.下列几何体中,柱体的个数是( )
A.5 B.4 C.3 D.2
3.观察下列图形并填空.
上面图形中,圆柱是___________,棱柱是___________,圆锥是__________,棱锥是__________,圆台是__________,棱台是___________,球体是____________.(填序号)
知识点二:几何体的组成
4.如图,下列几何体中,共有5个面的是( )
5.如图所示的火箭模型,头部和箭体中间的部分可以看成的立体图形为( )
A.棱锥与棱柱的组合体 B.圆锥与圆柱的组合体
C.棱锥与圆柱的组合体 D.圆锥与棱柱的组合体
6.在一个不透明的袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征.甲同学说:“它有4个面是三角形.”乙同学说:“它有 8条棱.”该模型的形状对应的立体图形可能是( )
A.三棱柱 B.四棱柱 C.三棱锥 D.四棱锥
7.如图所示的几何体由_________个面围成,面与面相交成__________条线,其中直线有__________条,曲线有__________条.
知识点三:棱柱的特征
8.下列各几何体中,直棱柱的个数是( )
A.5 B.4 C.3 D.2
9.如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫作棱锥.如图是一个四棱柱和一个六棱锥,它们各有12条棱.下列棱柱中和九棱锥的棱数相等的是( )
A.五棱柱 B.六棱柱 C.七棱柱 D.八棱柱
10.一个棱柱有 10个面,那么它的棱数是( )
A.16 B.20 C.22 D.24
能力提升
11.如图,从棱长为10的正方体的一个顶点处挖去一个棱长为4的小正方体,则剩下图形的所有棱长之和为( )
A.144 B.142 C.140 D.138
第11题图 第12题图
12.如图是由8个完全相同的小正方体搭成的几何体,若小正方体的棱长为1,则该几何体的表面积是( )
A.16 B.30 C.32 D.34
13.如图,模块①由15个棱长为1的小正方体构成,模块②~⑥均由4个棱长为1的小正方体构成.现在从模块②~⑥中选出三个模块放到模块①上,与模块①组成一个棱长为3的大正方体.下列四个方案中,符合上述要求的是( )
A.模块②④⑤ B.模块③④⑥ C.模块②③⑥ D.模块③⑤⑥
14.如图,一个圆柱形钢化玻璃容器的底面半径是 10cm,把一块浸没于水中的铁块从这个容器中取出后,水面下降2cm,则这块铁块的体积是_______cm .(铁块带出的水忽略不计)
15.如图是一个底面各边都相等的六棱柱,它的底面边长为 2cm,高为5cm.这个棱柱共有________条棱,________个面,侧面积是________cm .
第15题图 第16题图
16.(1)如图,补全图形,使之成为完整的长方体
(2)已知这个长方体的长、宽、高的比是6:5:3,长方体的棱长总和为168,则这个长
方体的长=_________,宽=________,高=_________.
17.如图所示的四个几何体分别是三棱柱、四棱柱、五棱柱和六棱柱,三棱柱有 5个面,9 条棱,6个顶点,观察图形,完成下面各题.
(1)四棱柱有________个面,________条棱,_______个顶点.
(2)五棱柱有________个面,________条棱,_______个顶点.
(3)由此猜想:n 棱柱有_______个面,_______条棱,________个顶点.
培优创新
18.如图是由若干个小三棱锥堆成的一个大三棱锥,把大三棱锥的四个面都涂上颜色.若把其中1个面涂色的小三棱锥叫中心块,2个面涂色的叫棱块,3个面涂色的叫角块,则“(中心块数)一(棱块数)一(角块数)”得( )
A.0 B.2 C.4 D.6
参考答案
1. C 2. A
3.④ ③⑥⑧ ①⑦ ② ⑨ ⑩ ⑤
4. C 5. B 6. D
7.4 6 4 2
8. C 9. B 10. D 11. A 12. D 13. C
14.200π
15.18 8 60
16.解:(1)图略. (2)18 15 9
17.(1)6 12 8 (2)7 15 10 (3)
18. B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
