简单线性规划
图片预览




文档简介
课件18张PPT。江苏省南通市第二中学 丁玉娟简单线性规划(复习课)复习目标:会作二元一次不等式表示的平面区域
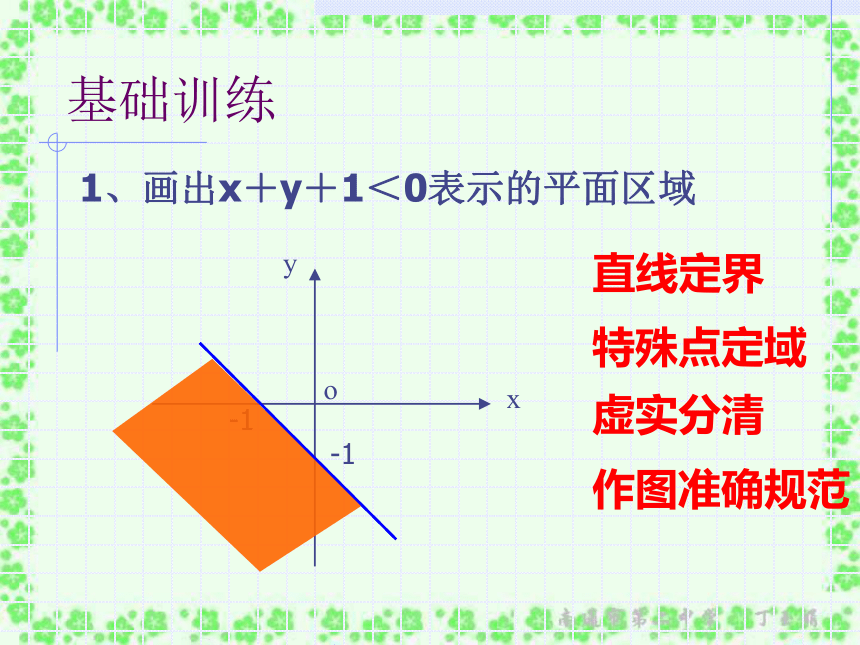
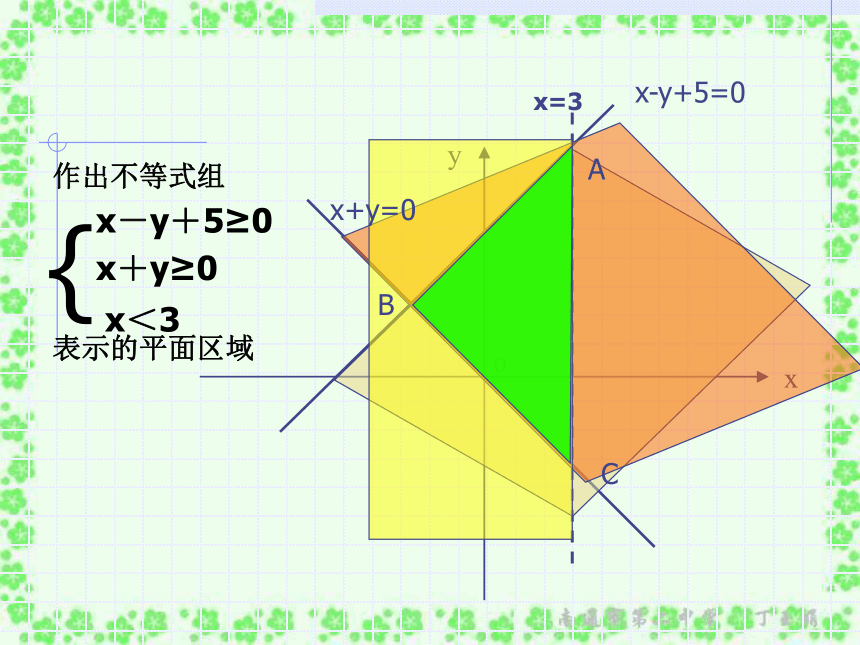
了解线性规划的意义,并会进行简单的应用基础训练1、画出x+y+1<0表示的平面区域 直线定界特殊点定域虚实分清作图准确规范2、作出不等式组{ 表示的平面区域?基础训练ABC{x=3作出不等式组
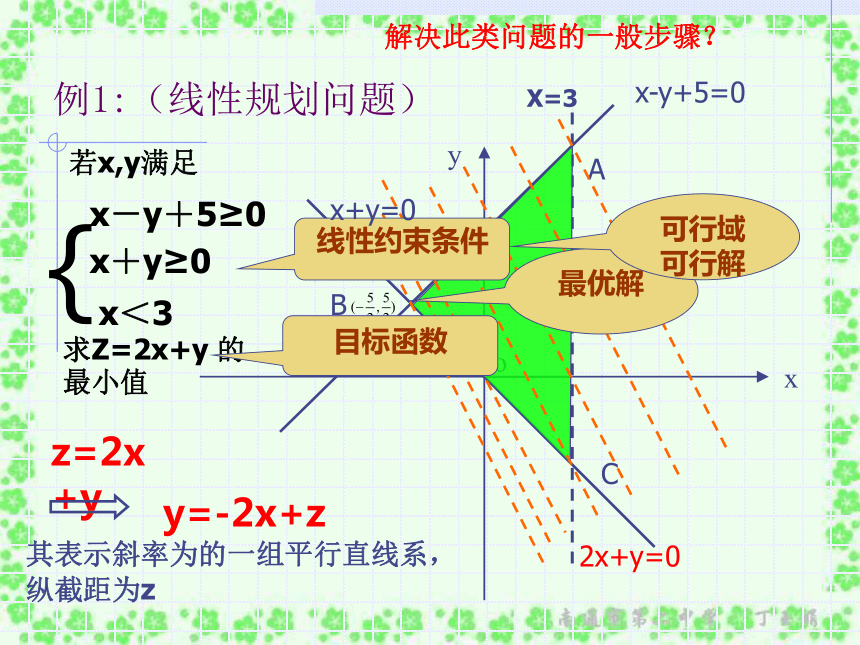
表示的平面区域x-y+5=0x+y=0ABC例1:(线性规划问题){X=3求Z=2x+y 的
最小值z=2x+y其表示斜率为的一组平行直线系,
纵截距为z若x,y满足最优解目标函数可行域
可行解解决此类问题的一般步骤?x-y+5=0x+y=02x+y=0解线性规划问题的步骤(2)移:在线性目标函数所表示的一组平行
线中,利用平移的方法找出与可行
域有公共点且纵截距最大或最小的
直线; (3)求:通过解方程组求出最优解; (4)答:作出答案。 (1)画:画出线性约束条件所表示的可行域;若x,y满足不等式组不等式组{ 例1:变题1、在上述的条件下,探求Z=2x-2y 的最值ABC例1(变题1):探求Z=2x-2y 的
最值
2x-2y=0充分理解几何意义
注意数形结合x+y=0x-y+5=0X=3ABC例1(变题2):x+y=0x-y+5=0X=3若在所在上述区域上有无穷多个点 可使目标函数 取最小值,则求 的值 ABC例1(变题3):K的几何意义:
由(x,y)和(-3,-3)确定的
直线斜率X=3x+y=0ABC例1(变题4):x-y+5=0x+y=0X=3例2. 某工厂生产甲、乙两种产品,生产1t甲种产品需要A种原料4t、B种原料12t,产生的利润为2万元;生产1t乙种产品需要A种原料1t、B 种原料9t,产生的利润为1万元.现有库存A 种原料10t、B种原料60t,如何安排生产才能使利润最大?并求出最大利润. 生产实际中的线性规划问题41221911060例2:生产实际中的线性规划问题解:设甲、乙两种产品分别生产x吨,y吨,利润为P万元
根据题意列出条件组得:{于是问题就转化为在这个条件组下,
求出x、y,使利润P=2x+y达到最大。解:解:设甲、乙两种产品分别生产x吨,y吨,利润为P万元
根据题意列出条件组得:于是问题转化为在此条件组下,求出x,y,使利润P=2x+y达到最大。4x+y=104x+3y=20xyOA(1.25,5)此时P的最大值为
1.25×2 +5 =7.5(万元).答:当甲、乙两种产品分别生产1.25吨、5吨时,利润最大,最大值为7.5万元。作出可行域(如下图),将目标函数变形为
y =-2x+ P,这是斜率为-2随P变化的一族
直线,P为直线在y轴上的截距,由图可知,使2x+y取得最大值的
(x,y)是当直线 与
的交点A(1.25, 5),先 建模: a根据题意,设出变量x、y b将已知条件列表,找出线性约束条件 c确定线性目标函数z=f(x,y)生产实际中的线性规划问题的图解法步骤 注意解题规范!小结归纳: 线性规划实际上是“数形结合”的数学思想的体现,是 一种求最值的方法。
1.二元一次不等式与平面区域
2.线性规划问题的意义及解题步骤3.生产实际中的线性规划问题的解法关注目标函数的几何意义.感谢指导!
了解线性规划的意义,并会进行简单的应用基础训练1、画出x+y+1<0表示的平面区域 直线定界特殊点定域虚实分清作图准确规范2、作出不等式组{ 表示的平面区域?基础训练ABC{x=3作出不等式组
表示的平面区域x-y+5=0x+y=0ABC例1:(线性规划问题){X=3求Z=2x+y 的
最小值z=2x+y其表示斜率为的一组平行直线系,
纵截距为z若x,y满足最优解目标函数可行域
可行解解决此类问题的一般步骤?x-y+5=0x+y=02x+y=0解线性规划问题的步骤(2)移:在线性目标函数所表示的一组平行
线中,利用平移的方法找出与可行
域有公共点且纵截距最大或最小的
直线; (3)求:通过解方程组求出最优解; (4)答:作出答案。 (1)画:画出线性约束条件所表示的可行域;若x,y满足不等式组不等式组{ 例1:变题1、在上述的条件下,探求Z=2x-2y 的最值ABC例1(变题1):探求Z=2x-2y 的
最值
2x-2y=0充分理解几何意义
注意数形结合x+y=0x-y+5=0X=3ABC例1(变题2):x+y=0x-y+5=0X=3若在所在上述区域上有无穷多个点 可使目标函数 取最小值,则求 的值 ABC例1(变题3):K的几何意义:
由(x,y)和(-3,-3)确定的
直线斜率X=3x+y=0ABC例1(变题4):x-y+5=0x+y=0X=3例2. 某工厂生产甲、乙两种产品,生产1t甲种产品需要A种原料4t、B种原料12t,产生的利润为2万元;生产1t乙种产品需要A种原料1t、B 种原料9t,产生的利润为1万元.现有库存A 种原料10t、B种原料60t,如何安排生产才能使利润最大?并求出最大利润. 生产实际中的线性规划问题41221911060例2:生产实际中的线性规划问题解:设甲、乙两种产品分别生产x吨,y吨,利润为P万元
根据题意列出条件组得:{于是问题就转化为在这个条件组下,
求出x、y,使利润P=2x+y达到最大。解:解:设甲、乙两种产品分别生产x吨,y吨,利润为P万元
根据题意列出条件组得:于是问题转化为在此条件组下,求出x,y,使利润P=2x+y达到最大。4x+y=104x+3y=20xyOA(1.25,5)此时P的最大值为
1.25×2 +5 =7.5(万元).答:当甲、乙两种产品分别生产1.25吨、5吨时,利润最大,最大值为7.5万元。作出可行域(如下图),将目标函数变形为
y =-2x+ P,这是斜率为-2随P变化的一族
直线,P为直线在y轴上的截距,由图可知,使2x+y取得最大值的
(x,y)是当直线 与
的交点A(1.25, 5),先 建模: a根据题意,设出变量x、y b将已知条件列表,找出线性约束条件 c确定线性目标函数z=f(x,y)生产实际中的线性规划问题的图解法步骤 注意解题规范!小结归纳: 线性规划实际上是“数形结合”的数学思想的体现,是 一种求最值的方法。
1.二元一次不等式与平面区域
2.线性规划问题的意义及解题步骤3.生产实际中的线性规划问题的解法关注目标函数的几何意义.感谢指导!
