湘教版八年级下册(新)第2章《四边形》同步测试
文档属性
| 名称 | 湘教版八年级下册(新)第2章《四边形》同步测试 |
|
|
| 格式 | zip | ||
| 文件大小 | 89.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-30 00:00:00 | ||
图片预览

文档简介
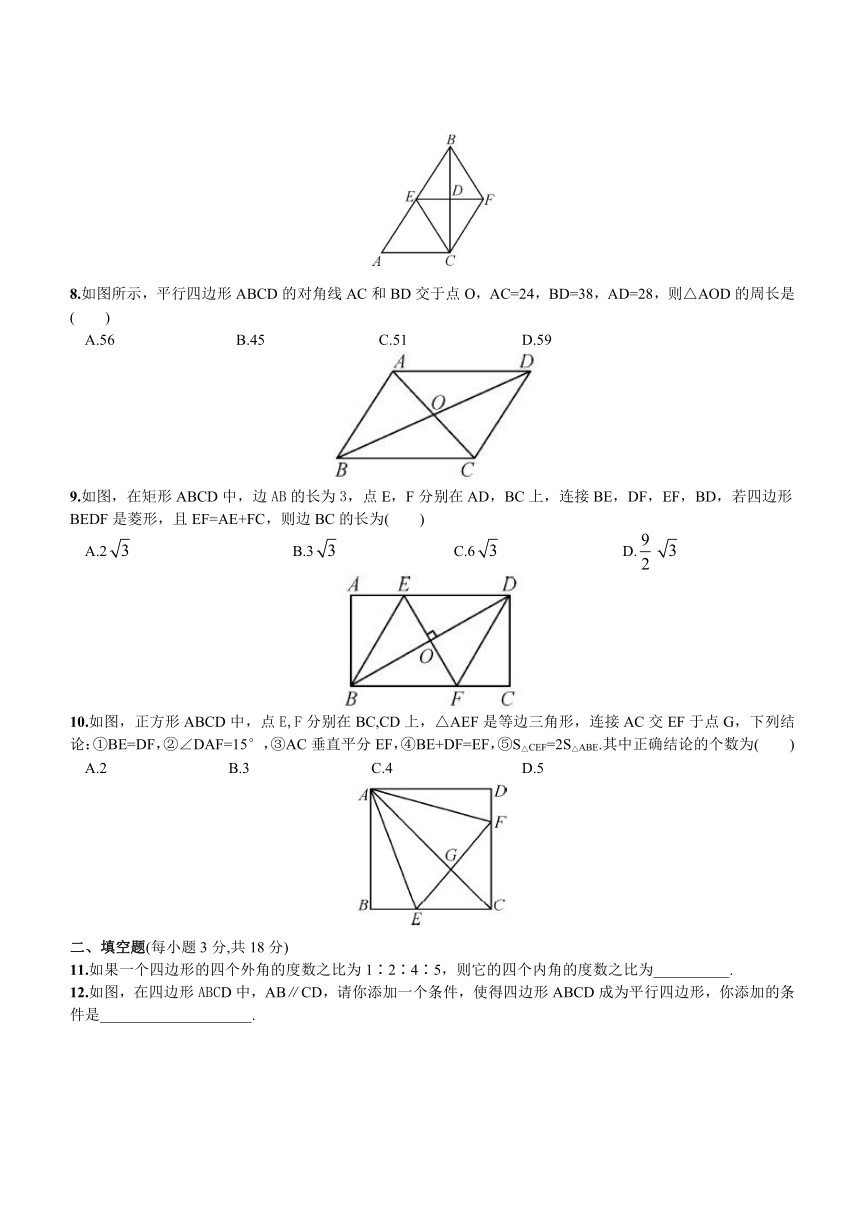
第2章 四边形
(时间:45分钟 满分:100分)
一、选择题(每小题3分,共30分)
1.一个十边形的每个内角都相等,则每个内角的度数为( )
A.90° B.144° C.36° D.18°
2.下列安全标志图中,是中心对称图形的是( )
( http: / / www.21cnjy.com )
3.如图,在□ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为( )
A.4 B.3 C. D.2
( http: / / www.21cnjy.com )
4.如图,以三角形的三个顶点及三边中点为顶点的平行四边形共有( )
A.1个 B.2个 C.3个 D.4个
( http: / / www.21cnjy.com )
5.平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.对角线互相垂直平分且相等
6.如图,菱形ABCD的周长是16,∠A=60°,则对角线BD的长度为( )
A.2 B.2 C.4 D.4
( http: / / www.21cnjy.com )
7.如图,在Rt△ABC中,∠ACB=9 ( http: / / www.21cnjy.com )0°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加一个条件,仍不能证明四边形BECF为正方形的是( )
A.BC=AC B.CF⊥BF C.BD=DF D.AC=BF
( http: / / www.21cnjy.com )
8.如图所示,平行四边形ABCD的对角线AC和BD交于点O,AC=24,BD=38,AD=28,则△AOD的周长是( )
A.56 B.45 C.51 D.59
( http: / / www.21cnjy.com )
9.如图,在矩形ABCD中,边AB的长为3 ( http: / / www.21cnjy.com ),点E,F分别在AD,BC上,连接BE,DF,EF,BD,若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
A.2 B.3 C.6 D.
( http: / / www.21cnjy.com )
10.如图,正方形ABCD中,点E,F分别 ( http: / / www.21cnjy.com )在BC,CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论的个数为( )
A.2 B.3 C.4 D.5
( http: / / www.21cnjy.com )
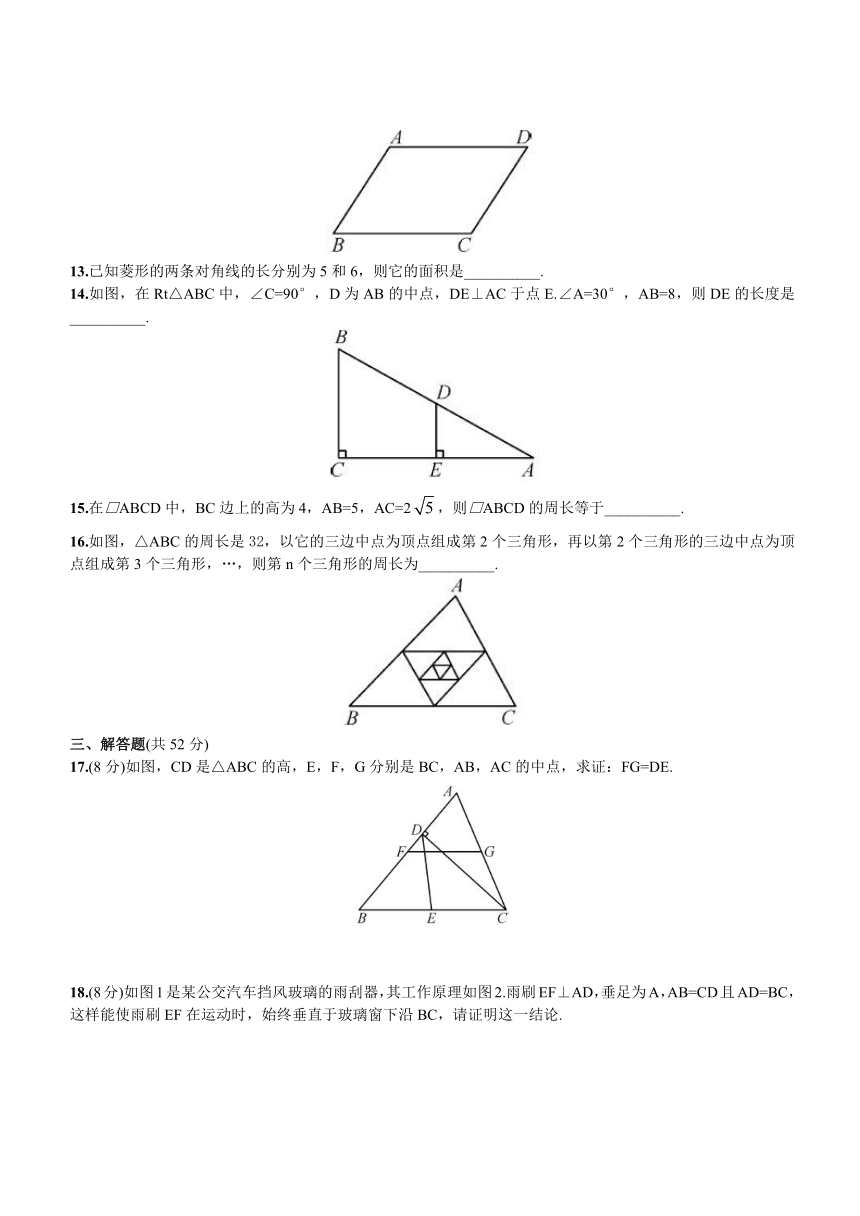
二、填空题(每小题3分,共18分)
11.如果一个四边形的四个外角的度数之比为1∶2∶4∶5,则它的四个内角的度数之比为__________.
12.如图,在四边形ABC ( http: / / www.21cnjy.com )D中,AB∥CD,请你添加一个条件,使得四边形ABCD成为平行四边形,你添加的条件是____________________.
( http: / / www.21cnjy.com )
13.已知菱形的两条对角线的长分别为5和6,则它的面积是__________.
14.如图,在Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AC于点E.∠A=30°,AB=8,则DE的长度是__________.
( http: / / www.21cnjy.com )
15.在□ABCD中,BC边上的高为4,AB=5,AC=2,则□ABCD的周长等于__________.
16.如图,△ABC的周长是32,以它 ( http: / / www.21cnjy.com )的三边中点为顶点组成第2个三角形,再以第2个三角形的三边中点为顶点组成第3个三角形,…,则第n个三角形的周长为__________.
( http: / / www.21cnjy.com )
三、解答题(共52分)
17.(8分)如图,CD是△ABC的高,E,F,G分别是BC,AB,AC的中点,求证:FG=DE.
( http: / / www.21cnjy.com )
18.(8分)如图1是某公交汽车挡 ( http: / / www.21cnjy.com )风玻璃的雨刮器,其工作原理如图2.雨刷EF⊥AD,垂足为A,AB=CD且AD=BC,这样能使雨刷EF在运动时,始终垂直于玻璃窗下沿BC,请证明这一结论.
( http: / / www.21cnjy.com )
19.(12分)如图,在四边形ABCD中,点H是边BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连接BE,CF.
( http: / / www.21cnjy.com )
(1)请你添加一个条件,使得△BEH≌△CFH,你添加的条件是____________________,并证明;
(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形,请说明理由.
20.(12分)如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
( http: / / www.21cnjy.com )
(1)求证:四边形OCED为菱形;
(2)连接AE、BE,AE与BE相等吗?请说明理由.
21.(12分)如图,△ABC中, ( http: / / www.21cnjy.com )AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
( http: / / www.21cnjy.com )
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
参考答案
1.B 2.B 3.B 4.C 5.A 6.C 7.D 8.D 9.B 10.C
11.5∶4∶2∶1
12.答案不唯一,如:AB=CD或AD∥BC或∠A=∠C或∠A+∠B=180°等
13.15 14.2 15.12或20 16.26-n
17.证明:∵F,G分别是AB,AC的中点,
∴FG=BC.
∵CD是△ABC的高,
∴△BCD是直角三角形.
∵点E是BC的中点,
∴DE=BC.
∴FG=DE.
18.证明:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
∴AD∥BC.
∵EF⊥AD,
∴EF⊥BC.
19.(1)添加条件:BE∥CF(答案不唯一).
证明:∵BE∥CF,
∴∠EBH=∠FCH.
∵点H是边BC的中点,
∴BH=CH.
∵∠BHE=∠CHF,
∴△BEH≌△CFH(ASA).
(2)当BH=EH时,四边形BFCE是矩形.
理由如下:
∵△BEH≌△CFH,
∴BH=CH,EH=FH.
∴四边形BFCE是平行四边形.
又∵BH=EH,
∴EF=BC.
∴四边形BFCE是矩形.
20.(1)证明:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形.
又∵AC,BD为矩形ABCD的对角线,
∴OC=OD.
∴平行四边形OCED为菱形.
(2)AE与BE相等.
理由如下:
由(1)可知平行四边形OCED为菱形,
∴ED=EC,
∴∠EDC=∠ECD.
又∵四边形ABCD为矩形,
∴AD=BC,∠ADC=∠BCD.
∴∠EDC+∠ADC=∠BCD+∠ECD.
∴∠ADE=∠BCE,
∴△ADE≌△BCE(SAS).
∴AE=BE.
21.(1)证明:∵点O为AB的中点,
∴OA=OB.
又∵OE=OD,
∴四边形AEBD是平行四边形.
∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC.
∴四边形AEBD是矩形.
(2)当△ABC是等腰直角三角形时,矩形AEBD是正方形.
理由:∵△ABC是等腰直角三角形,
∴∠BAD=∠CAD=∠DBA=45°.
∴BD=AD.
由(1)知四边形AEBD是矩形,
∴四边形AEBD是正方形.
(时间:45分钟 满分:100分)
一、选择题(每小题3分,共30分)
1.一个十边形的每个内角都相等,则每个内角的度数为( )
A.90° B.144° C.36° D.18°
2.下列安全标志图中,是中心对称图形的是( )
( http: / / www.21cnjy.com )
3.如图,在□ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为( )
A.4 B.3 C. D.2
( http: / / www.21cnjy.com )
4.如图,以三角形的三个顶点及三边中点为顶点的平行四边形共有( )
A.1个 B.2个 C.3个 D.4个
( http: / / www.21cnjy.com )
5.平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.对角线互相垂直平分且相等
6.如图,菱形ABCD的周长是16,∠A=60°,则对角线BD的长度为( )
A.2 B.2 C.4 D.4
( http: / / www.21cnjy.com )
7.如图,在Rt△ABC中,∠ACB=9 ( http: / / www.21cnjy.com )0°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加一个条件,仍不能证明四边形BECF为正方形的是( )
A.BC=AC B.CF⊥BF C.BD=DF D.AC=BF
( http: / / www.21cnjy.com )
8.如图所示,平行四边形ABCD的对角线AC和BD交于点O,AC=24,BD=38,AD=28,则△AOD的周长是( )
A.56 B.45 C.51 D.59
( http: / / www.21cnjy.com )
9.如图,在矩形ABCD中,边AB的长为3 ( http: / / www.21cnjy.com ),点E,F分别在AD,BC上,连接BE,DF,EF,BD,若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
A.2 B.3 C.6 D.
( http: / / www.21cnjy.com )
10.如图,正方形ABCD中,点E,F分别 ( http: / / www.21cnjy.com )在BC,CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论的个数为( )
A.2 B.3 C.4 D.5
( http: / / www.21cnjy.com )
二、填空题(每小题3分,共18分)
11.如果一个四边形的四个外角的度数之比为1∶2∶4∶5,则它的四个内角的度数之比为__________.
12.如图,在四边形ABC ( http: / / www.21cnjy.com )D中,AB∥CD,请你添加一个条件,使得四边形ABCD成为平行四边形,你添加的条件是____________________.
( http: / / www.21cnjy.com )
13.已知菱形的两条对角线的长分别为5和6,则它的面积是__________.
14.如图,在Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AC于点E.∠A=30°,AB=8,则DE的长度是__________.
( http: / / www.21cnjy.com )
15.在□ABCD中,BC边上的高为4,AB=5,AC=2,则□ABCD的周长等于__________.
16.如图,△ABC的周长是32,以它 ( http: / / www.21cnjy.com )的三边中点为顶点组成第2个三角形,再以第2个三角形的三边中点为顶点组成第3个三角形,…,则第n个三角形的周长为__________.
( http: / / www.21cnjy.com )
三、解答题(共52分)
17.(8分)如图,CD是△ABC的高,E,F,G分别是BC,AB,AC的中点,求证:FG=DE.
( http: / / www.21cnjy.com )
18.(8分)如图1是某公交汽车挡 ( http: / / www.21cnjy.com )风玻璃的雨刮器,其工作原理如图2.雨刷EF⊥AD,垂足为A,AB=CD且AD=BC,这样能使雨刷EF在运动时,始终垂直于玻璃窗下沿BC,请证明这一结论.
( http: / / www.21cnjy.com )
19.(12分)如图,在四边形ABCD中,点H是边BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连接BE,CF.
( http: / / www.21cnjy.com )
(1)请你添加一个条件,使得△BEH≌△CFH,你添加的条件是____________________,并证明;
(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形,请说明理由.
20.(12分)如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
( http: / / www.21cnjy.com )
(1)求证:四边形OCED为菱形;
(2)连接AE、BE,AE与BE相等吗?请说明理由.
21.(12分)如图,△ABC中, ( http: / / www.21cnjy.com )AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
( http: / / www.21cnjy.com )
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
参考答案
1.B 2.B 3.B 4.C 5.A 6.C 7.D 8.D 9.B 10.C
11.5∶4∶2∶1
12.答案不唯一,如:AB=CD或AD∥BC或∠A=∠C或∠A+∠B=180°等
13.15 14.2 15.12或20 16.26-n
17.证明:∵F,G分别是AB,AC的中点,
∴FG=BC.
∵CD是△ABC的高,
∴△BCD是直角三角形.
∵点E是BC的中点,
∴DE=BC.
∴FG=DE.
18.证明:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
∴AD∥BC.
∵EF⊥AD,
∴EF⊥BC.
19.(1)添加条件:BE∥CF(答案不唯一).
证明:∵BE∥CF,
∴∠EBH=∠FCH.
∵点H是边BC的中点,
∴BH=CH.
∵∠BHE=∠CHF,
∴△BEH≌△CFH(ASA).
(2)当BH=EH时,四边形BFCE是矩形.
理由如下:
∵△BEH≌△CFH,
∴BH=CH,EH=FH.
∴四边形BFCE是平行四边形.
又∵BH=EH,
∴EF=BC.
∴四边形BFCE是矩形.
20.(1)证明:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形.
又∵AC,BD为矩形ABCD的对角线,
∴OC=OD.
∴平行四边形OCED为菱形.
(2)AE与BE相等.
理由如下:
由(1)可知平行四边形OCED为菱形,
∴ED=EC,
∴∠EDC=∠ECD.
又∵四边形ABCD为矩形,
∴AD=BC,∠ADC=∠BCD.
∴∠EDC+∠ADC=∠BCD+∠ECD.
∴∠ADE=∠BCE,
∴△ADE≌△BCE(SAS).
∴AE=BE.
21.(1)证明:∵点O为AB的中点,
∴OA=OB.
又∵OE=OD,
∴四边形AEBD是平行四边形.
∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC.
∴四边形AEBD是矩形.
(2)当△ABC是等腰直角三角形时,矩形AEBD是正方形.
理由:∵△ABC是等腰直角三角形,
∴∠BAD=∠CAD=∠DBA=45°.
∴BD=AD.
由(1)知四边形AEBD是矩形,
∴四边形AEBD是正方形.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
