六年级上册数学北师大版6 圆的面积(二) 课件(共23张PPT)
文档属性
| 名称 | 六年级上册数学北师大版6 圆的面积(二) 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-21 10:04:17 | ||
图片预览







文档简介
(共23张PPT)
北师大版六年级数学上册《圆》
《圆的面积(二)》
课前复习:
1、圆的面积是指:
圆所占平面的大小
2、圆的面积近似
平行四边形的高是圆的
平行四边形的底是圆的
3、圆的面积公式是
平行四边形
半径
周长的一半
沿线剪开
周长
半径
探究新知—公式的推导
r
2πr
πr
把圆形茶杯垫片沿直线剪开,得到两个近似的三角
形,再拼成平行四边形。
周长的一半
半径
3m
3.14×32
=3.14×9
=28.26(m2)
答:能浇灌28.26平方米的农田。
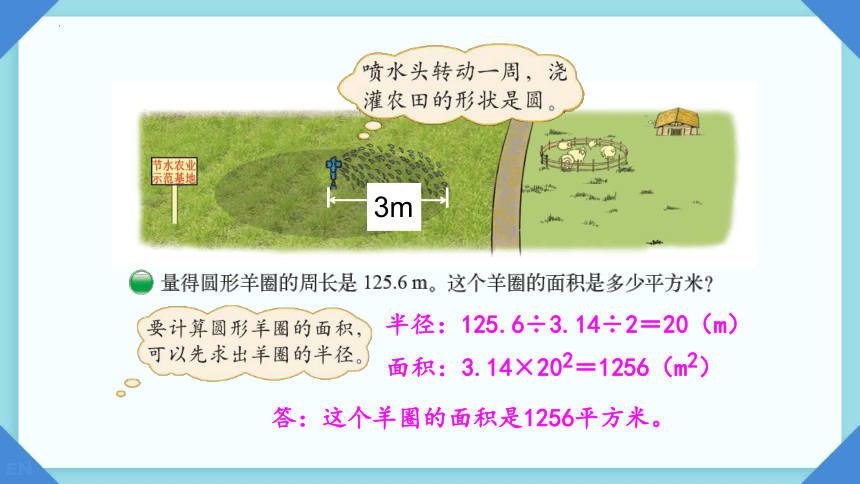
3m
半径:125.6÷3.14÷2=20(m)
答:这个羊圈的面积是1256平方米。
面积:3.14×202=1256(m2)
两个大小不同的圆组成
两个圆的圆心在同一个点上
共同特征
同心圆
探究活动-圆环的面积
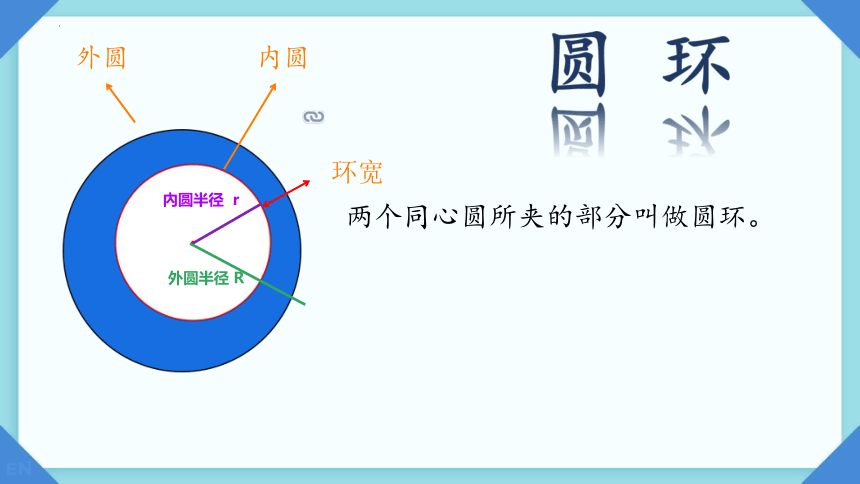
內圆半径 r
外圆半径 R
外圆
内圆
两个同心圆所夹的部分叫做圆环。
圆 环
环宽
环宽
r
R
r表示内圆半径
R表示外圆半径
R=r+环宽
R、r、环宽它们彼此之间有什么关系呢?
如何计算圆环的面积呢?
圆环的面积:
大圆的面积减去小圆的面积
在大圆中间挖去一个小圆,剩下的部分就形成了一个圆环
S环 =πR2-πr2
圆环的面积 =大圆的面积-小圆的面积
S环 =π(R2 - r2)
探究圆环面积的计算方法:
R
r
大圆的面积:
小圆的面积:
乘法 分配律
小结:
1、光盘的银色部分是一个圆环,内圆半径是2cm,
外圆半径是6cm,圆环的面积是多少?
3.14 - 3.14
= 3.14 36 - 3.14 4
= 113.04 - 12.56
=100.48 (cm2 )
答:圆环的面积是100.48cm2。
S环 = π(R2 - r2)
S环 =πR2 -πr2
3.14 (62-22)
= 3.14 (36 - 4)
= 3.14 32
=100.48 (cm2 )
答:圆环的面积是100.48cm2。
典型例题
2、右图是一块玉璧,外直径是10cm,内直径是6cm,
这块玉璧的面积是多少?
1、先求出两个圆的半径分别是多少
R大=10÷2=5(cm)
r小=6÷2=3(cm)
分析:圆环的面积=大圆的面积-小圆的面积
或
=50.24( )
=3.14×52-3.14×32
=50.24( )
1.一个圆形杯垫的半径是4cm,这个杯垫的面积是多少平方厘米?
3.14×(4×4)=50.24(cm )
答:这个杯垫的面积是50.24平方厘米。
2.有一圆形蓄水池。它的周长是31.4m,它的占地面积约是多少?
31.4÷3.14÷2=5(m)
3.14×(5×5)=78.5(平方米)
答:水池的占地面积是78.5平方米。
半径:
面积:
4.北京天坛公园的回音壁是闻名世界的声学奇迹,它是一道圆形围墙。圆的直径约为61.5米,周长与面积分别是多少?(结果保留一位小数)
周长:31.4×61.5≈193.1(m)
面积:31.4×(61.5÷2)2
≈2969.1(m2)
5.一个运动场跑道的形状与大小如图。两边是半圆形,中间是长方形,这个运动场的占地面积是多少?
长方形面积:50×20=1000(m2)
圆面积:3.14×(20÷2)2=314(m2)
占地面积:1000+314=1314(m2)
阴影部分的面积=大圆面积-小圆面积
3.14×122-3.14×82
=251.2(cm2)
=3.14×(122-82)
=3.14×(144-64)
6.求下图中阴影部分的面积。
阴影部分的面积=圆面积-正方形面积
圆的面积:3.14×(10÷2)2=78.5(cm2)
正方形面积:10×(10÷2)÷2×2
=50(cm2)
阴影部分面积:78.5-50=28.5(cm2)
6.求下图中阴影部分的面积。
d=2r
圆的半径、直径、周长之间的计算。
C
r
d
r=d÷2
c=πd
d=c÷π
C=2πr
r=c÷π÷2
北师大版六年级数学上册《圆》
《圆的面积(二)》
课前复习:
1、圆的面积是指:
圆所占平面的大小
2、圆的面积近似
平行四边形的高是圆的
平行四边形的底是圆的
3、圆的面积公式是
平行四边形
半径
周长的一半
沿线剪开
周长
半径
探究新知—公式的推导
r
2πr
πr
把圆形茶杯垫片沿直线剪开,得到两个近似的三角
形,再拼成平行四边形。
周长的一半
半径
3m
3.14×32
=3.14×9
=28.26(m2)
答:能浇灌28.26平方米的农田。
3m
半径:125.6÷3.14÷2=20(m)
答:这个羊圈的面积是1256平方米。
面积:3.14×202=1256(m2)
两个大小不同的圆组成
两个圆的圆心在同一个点上
共同特征
同心圆
探究活动-圆环的面积
內圆半径 r
外圆半径 R
外圆
内圆
两个同心圆所夹的部分叫做圆环。
圆 环
环宽
环宽
r
R
r表示内圆半径
R表示外圆半径
R=r+环宽
R、r、环宽它们彼此之间有什么关系呢?
如何计算圆环的面积呢?
圆环的面积:
大圆的面积减去小圆的面积
在大圆中间挖去一个小圆,剩下的部分就形成了一个圆环
S环 =πR2-πr2
圆环的面积 =大圆的面积-小圆的面积
S环 =π(R2 - r2)
探究圆环面积的计算方法:
R
r
大圆的面积:
小圆的面积:
乘法 分配律
小结:
1、光盘的银色部分是一个圆环,内圆半径是2cm,
外圆半径是6cm,圆环的面积是多少?
3.14 - 3.14
= 3.14 36 - 3.14 4
= 113.04 - 12.56
=100.48 (cm2 )
答:圆环的面积是100.48cm2。
S环 = π(R2 - r2)
S环 =πR2 -πr2
3.14 (62-22)
= 3.14 (36 - 4)
= 3.14 32
=100.48 (cm2 )
答:圆环的面积是100.48cm2。
典型例题
2、右图是一块玉璧,外直径是10cm,内直径是6cm,
这块玉璧的面积是多少?
1、先求出两个圆的半径分别是多少
R大=10÷2=5(cm)
r小=6÷2=3(cm)
分析:圆环的面积=大圆的面积-小圆的面积
或
=50.24( )
=3.14×52-3.14×32
=50.24( )
1.一个圆形杯垫的半径是4cm,这个杯垫的面积是多少平方厘米?
3.14×(4×4)=50.24(cm )
答:这个杯垫的面积是50.24平方厘米。
2.有一圆形蓄水池。它的周长是31.4m,它的占地面积约是多少?
31.4÷3.14÷2=5(m)
3.14×(5×5)=78.5(平方米)
答:水池的占地面积是78.5平方米。
半径:
面积:
4.北京天坛公园的回音壁是闻名世界的声学奇迹,它是一道圆形围墙。圆的直径约为61.5米,周长与面积分别是多少?(结果保留一位小数)
周长:31.4×61.5≈193.1(m)
面积:31.4×(61.5÷2)2
≈2969.1(m2)
5.一个运动场跑道的形状与大小如图。两边是半圆形,中间是长方形,这个运动场的占地面积是多少?
长方形面积:50×20=1000(m2)
圆面积:3.14×(20÷2)2=314(m2)
占地面积:1000+314=1314(m2)
阴影部分的面积=大圆面积-小圆面积
3.14×122-3.14×82
=251.2(cm2)
=3.14×(122-82)
=3.14×(144-64)
6.求下图中阴影部分的面积。
阴影部分的面积=圆面积-正方形面积
圆的面积:3.14×(10÷2)2=78.5(cm2)
正方形面积:10×(10÷2)÷2×2
=50(cm2)
阴影部分面积:78.5-50=28.5(cm2)
6.求下图中阴影部分的面积。
d=2r
圆的半径、直径、周长之间的计算。
C
r
d
r=d÷2
c=πd
d=c÷π
C=2πr
r=c÷π÷2
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
