苏科版八年级数学上册试题 第2章《轴对称图形》章节测试卷(含答案详解)
文档属性
| 名称 | 苏科版八年级数学上册试题 第2章《轴对称图形》章节测试卷(含答案详解) |
|
|
| 格式 | docx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-22 08:05:54 | ||
图片预览




文档简介
第2章《轴对称图形》章节测试卷
一、选择题(本题共10小题,每小题3分,共30分。)
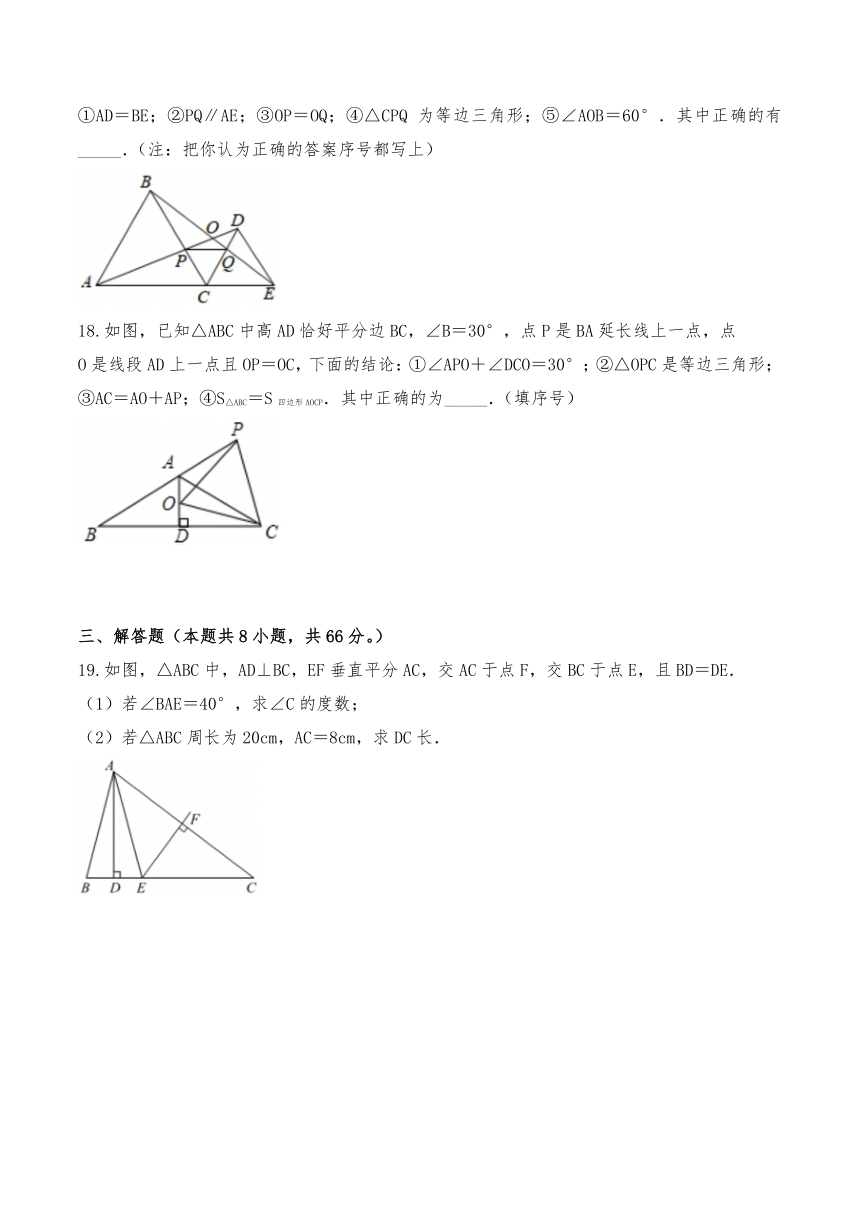
1.室内墙壁上挂一平面镜,小明在平面镜内看到他背后墙上时钟的示数如图所示,则这时的实际时间应是( )
A.3:20 B.3:40 C.4:40 D.8:20
2.下列说法中:①关于某直线成轴对称的两个图形一定能完全重合;②线段是轴对称图形;③有一条公共边的两个全等三角形一定关于公共边所在直线对称;④关于某条直线对称的两个图形一定分别位于该直线的两侧.正确有( )
A.1个 B.2个 C.3个 D.4个
3.如图,射线AB与射线CD平行,点F在射线AB上,∠DCF=70°,AF=a(a为常数,且a>0),P为射线CD上的一动点(不包括端点C),将△CPF沿PF翻折得到△EPF,连接AE,则AE最大时,∠DPE的度数为( )
A.30° B.55° C.70° D.90°
4.如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE.如果∠A=α,∠DEA=β,∠CEA'=γ,∠BDA'=θ,那么下列式子中不一定成立的是( )
A.θ=2α+γ B.θ+α+γ=180° C.90+=β D.a+β=90°+
5.如图,AB∥CD,AD∥BC,AD⊥CD,点E为线段BC上一点,将线段AB沿AE折叠,点B的对应点F落在四边形ABCD外侧,连接EF,若AF∥BD,∠ADB=α,则∠DAE为( )
A.α B.90° 2α C.45°+ D.45°
6.如图,△ABC的两条内角平分线相交于点D,过点D作一条平分△ABC面积的直线,那么这条直线分成的两个图形的周长比是( )
A.2:1 B.1:1 C.2:3 D.3:1
7.如图,在△ABC中.AB=AC.BC=4,△ABC的面积是24,AC的垂直平分线EF分别交AC,AB边于点E,F,若点D为BC边的中点,点M为线段EF上一动点,连接CM,DM,则CM+DM的最小值为( )
A.6 B.10 C.12 D.13
8.如图所示,∠AOB=60°,点P是∠AOB内一定点,并且OP=2,点M、N分别是射线OA,OB上异于点O的动点,当△PMN的周长取最小值时,点O到线段MN的距离为( )
A.1 B.2 C.4 D.1.5
9.在等边△ABC中,D、E分别为AB、AC边上的动点,BD=2AE,连接DE,以DE为边在△ABC内作等边△DEF,连接CF,当D从点A向B运动(不运动到点B)时,∠ECF大小的变化情况是( )
A.不变 B.变小 C.先变大 D.先变大后变小
10.如图,在△ABC中,∠BAC和∠ABC的平分线AE,BF相交于点O,AE交BC于E,BF交AC于F,过点O作OD⊥BC于D,下列三个结论:①∠AOB=90°+∠C;②当∠C=60°时,AF+BE=AB;③若OD=a,AB+BC+CA=2b,则S△ABC=ab.其中正确的是( )
A.①② B.②③ C.①②③ D.①③
二、填空题(本题共8小题,每小题3分,共24分。)
11.墙上有一个数字式电子钟,在对面墙上的镜子里看到该电子钟显示的时间如图所示,那么它的实际时间是_____.
12.如图,直线L为线段AB的垂直平分线,交AB于M,在直线L上取一点C1,使得MC1=MB,得到第一个三角形ABC1;在射线MC1上取一点C2,使得C1C2=BC1;得到第二个三角形△ABC2;在射线MC1上取一点C3,使得C2C3=BC2,得到第三个三角形△ABC3…依次这样作下去,则第2022个三角形△ABC2022中∠AC2022B的度数为_____.
13.如图,在Rt△ABC中,∠A=90°,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=2,则BC的长为_____.
14.如图,在△ABC中,AD平分∠BAC,交BC于点D,BE⊥AD于E,AB=6,AC=14,∠ABC=3∠C.则BE=_____.
15.如图,六边形ABCDEF中,∠A=∠B=∠C=∠D=∠E=∠F,且AB+BC=11,FA CD=3,则BC+DE=_____.
16.如图,△ABC是等边三角形,点D在AB上,AD=3BD,∠ACE=∠ADC,CE=CD.G是AC延长线上一点,EG∥AB.连接BE交AC于点F,则的值为_____.
17.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:
①AD=BE;②PQ∥AE;③OP=OQ;④△CPQ为等边三角形;⑤∠AOB=60°.其中正确的有_____.(注:把你认为正确的答案序号都写上)
18.如图,已知△ABC中高AD恰好平分边BC,∠B=30°,点P是BA延长线上一点,点
O是线段AD上一点且OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP.其中正确的为_____.(填序号)
三、解答题(本题共8小题,共66分。)
19.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
(1)若∠BAE=40°,求∠C的度数;
(2)若△ABC周长为20cm,AC=8cm,求DC长.
20.如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,交AC于D,AE⊥BD,垂足为E.求证:AC=2BE.
21.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=12cm.动点P从点A出发,沿AB向点B运动,动点Q从点B出发,沿BC向点C运动,如果动点P以2cm/s,Q以1cm/s的速度同时出发,设运动时间为t(s),解答下列问题:
(1)t为多少时,△PBQ是等边三角形?
(2)P、Q在运动过程中,△PBQ的形状不断发生变化,当t为多少时,△PBQ是直角三角形?请说明理由.
22.如图,在△ABC中,∠A=60°.BE,CF交于点P,且分别平分∠ABC,∠ACB.
(1)求∠BPC的度数;
(2)连接EF,求证:△EFP是等腰三角形.
23.已知OB,OC分别是△ABC的内角∠ABC和外角∠ACE的角平分线.
(1)在图1中,已知∠O=25°,求∠BAC的度数.
(2)连接OA,如图2,证明OA是外角∠CAD的角平分线.
(3)在图2中,已知S△BOC=16,BC=4,AC=5,AB=6,直接写出△ABC的面积.
24.△ABC中,∠ACB=90°,AC=BC,点D是BC边上的一个动点,连接AD,过点B作BF⊥AD于点F.
(1)如图1,分别延长AC,BF相交于点E,求证:BE=AD;
(2)如图2,若AD平分∠BAC,AD=5,求BF的长;
(3)如图3,M是FB延长线上一点,AD平分∠MAC,试探究AC,CD,AM之间的数量关系并说明理由.
25.已知:在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC边中点.点M为线段BC上的一个动点(不与点C,点D重合),连接AM,将线段AM绕点M顺时针旋转90°,得到线段ME,连接EC.
(1)如图1,若点M在线段BD上,求∠MCE的度数.
(2)如图2,若点M在线段CD上,试探究线段AC、CE、CM之间的数量关系,并证明你的结论.
26.在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系.
(1)如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是_____;
(2)如图2,点M、N在边AB、AC上,且当DM≠DN时,猜想(1)问的结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.
(3)如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.
答案
一、选择题
1.B
【解析】根据镜面对称的性质,分析可得题中所显示的时刻与3:40呈轴对称,所以此时的实际时间为3:40;
故本题选B。
2.B
【解析】①关于某直线成轴对称的两个图形一定能完全重合,正确;
②线段是轴对称图形,正确;
③有一条公共边的两个全等三角形不一定关于公共边所在的直线对称,错误;
④关于某条直线对称的两个图形不一定分别位于该直线的两侧,错误;
所以正确的个数是2个;
故本题选B。
3.C
【解析】∵CD∥AB,∠DCF=70°,∴∠DCF=∠CFA=70°,
由折叠性质知,EF=CF,
∵CF的长度为定值,∴当点E在AB上时,点E到点A的距离最大,如图,
由折叠知,∠PEF=∠DCF=70°,
∵CD∥AB,∴∠DPB=∠PEF=70°;
故本题选C。
4.B
【解析】如图,
∵∠A=∠A'=α,∴θ=∠A+∠DFA=∠A+∠A′+γ=2α+γ,
故A选项成立,不符合题意;
∵∠DEA=∠DEA′=β,∴∠DEA+∠DEA′ ∠FEA′=180°,
即2β γ=180°,∴90°+=β,
故C选项成立,不符合题意;
∵∠FDE=∠ADE,θ+∠FDE+∠ADE=180°,∴∠FDE=,
∵α+β=θ+∠FDE,∴α+β=θ+,即α+β=90°+,
故D选项成立,不符合题意;
故本题选B。
5.D
【解析】设∠DAE=x,
∵AB∥CD,AD⊥CD,∴AB⊥AD,∴∠BAD=90°,
∴∠BAE=∠BAD ∠DAE=90° x,
由折叠的性质得:∠FAE=∠BAE=90° x,
∴∠FAD=∠FAE ∠DAE=90° 2x,
∵AF∥BD,∴∠FAD=∠ADB=α,∴90° 2x=α,
解得:x=45° ,即∠DAE=45° ;
故本题选D。
6.B
【解析】连接AD,过D点作DE⊥AB于点E,作DF⊥AC于点F,作DG⊥BC于点G,
∵△ABC的两条内角平分线相交于点D,∴DE=DF=DG,
设MN平分△ABC的面积,则S△BDM+S△BDN=S△ADM+S△ADC+S△DCN,
∵S△BDM=BM DE,S△ADM=AM DE,S△ADC=AC DF,S△DCN=NC DG,S△BDN=BN DG,
∴BM DE+BN DG=AM DE+AC DF+NC DG,
∴BM+BN=AM+AC+NC,
∴BM+BN+MN=AM+AC+NC+MN,
即这条直线分成的两个图形的周长比是1:1;
故本题选B。
7.C
【解析】解:连接AD,
∵△ABC是等腰三角形,点D是BC边的中点.
∴AD⊥BC,∴S△ABC=BC AD=×4×AD=24,解得AD=12,
∵EF是线段AB的垂直平分线,
∴点C关于直线EF的对称点为点A,
连接AM,则CM+DM=AM+DM≥AD,
∴当点M在线段AD上时,CM+DM的值最小,
∴AD的长为CM+MD的最小值;
故本题选C。
8.A
【解析】分别作点P关于OB和OA的对称点P'和P'',连接OP'、OP''、P'P'',则P'P''与OB的交点为点N',P'P''与OA的交点为点M',
连接PN'、PM',则此时P'P''的值即为△PMN的周长的最小值,过点O作OC⊥P'P''于点C,如图所示:
由对称性可知OP=OP'=OP'',
∵∠AOB=60°,∴∠P'OP''=2×60°=120°,
∴∠OP'P''=∠OP''P'=30°,
∵OP=2,OC⊥P'P'',∴OC=OP'=1;
故本题选A。
9.A
【解析】在AC上截取CN=AE,连接FN,如图所示:
∵△ABC是等边三角形,∴∠A=60°,AB=AC,
∵BD=2AE,∴AD=NE,
∵△DEF是等边三角形,
∴DE=EF,∠DEF=60°,
∵∠ADE=180° ∠A ∠AED=180° 60° ∠AED=120° ∠AED,
∠NEF=180° ∠DEF ∠AED=180° 60° ∠AED=120° ∠AED,
∴∠ADE=∠NEF,
在△ADE和△NEF中,
∴△ADE≌△NEF(SAS),∴AE=FN,∠FNE=∠A=60°,
∴FN=CN,∴∠NCF=∠NFC,
∵∠FNE=∠NCF+∠NFC=60°,∴∠NCF=30°,即∠ECF=30°;
故本题选A。
10.C
【解析】∵∠BAC和∠ABC的平分线相交于点O,
∴∠OBA=∠CBA,∠OAB=∠CAB,
∴∠AOB=180° ∠OBA ∠OAB=180° ∠CBA ∠CAB
=180° (180° ∠C)=90°+∠C,故①正确;
∵∠C=60°,由①知:∠AOB=90°+∠C,∴∠AOB=120°,
∴∠AOF=60°,∴∠BOE=60°,
如图,在AB上取一点H,使BH=BE,
∵BF是∠ABC的角平分线,∴∠HBO=∠EBO,
在△HBO和△EBO中,
∴△HBO≌△EBO(SAS),∴∠BOH=∠BOE=60°,
∴∠AOH=180° 60° 60°=60°,∴∠AOH=∠AOF,
∵AE是∠BAC的角平分线,∴∠HAO=∠FAO,
在△HAO和△FAO中,
∴△HAO≌△FAO(ASA),∴AF=AH,
∴AB=BH+AH=BE+AF,故②正确;
作OH⊥AC于H,OM⊥AB于M,
∵∠BAC和∠ABC的平分线相交于点O,∴OH=OM=OD=a,
∵AB+AC+BC=2b,
∴S△ABC=×AB×OM+×AC×OH+×BC×OD=(AB+AC+BC) a=ab,
故③正确;
故本题选C。
二、填空题
11.12:51
【解析】根据镜面对称的性质,分析可得题中所显示的图片与12:51成轴对称,所以此时实际时刻为12:51;
故本题答案为:12:51。
12.
【解析】由于直线L为线段AB的垂直平分线,
∴C1A=C1B,C2A=C2B,C3A=C3B,…
∵C1C2=BC1,∴C1C2=BC1=AC1,
∴∠C1C2A=∠C1AC2=∠AC1M,∠C1C2B=∠C1BC2=∠BC1M,
∴∠AC2B=∠AC1B,
同理,∴∠AC3B=∠AC2B=×∠AC1B,
∴∠AC4B=∠AC3B=××∠AC1B,
∴∠AC5B=∠AC4B=×××∠AC1B,
…
∴∠AC2022B=()2021∠AC1B=;
故本题答案为:。
13.12
【解析】∵CM平分∠ACB,MN平分∠AMC,∴∠ACM=∠BCM,∠AMN=∠CMN,
∵MN∥BC,∴∠AMN=∠CMN=∠ACM=∠BCM,∴MN=CN,
∵∠A=90°,∴∠AMN=∠CMN=∠ACM=∠BCM=30°,
∵AN=2,∴MN=CN=4,∴AC=6,
∵MN∥BC,∴∠B=∠AMN=30°,∴BC=2AC=12;
故本题答案为:12。
14.4
【解析】延长BE交AC于G,
∵AD平分∠BAC,∴∠GAE=∠BAE,
∵BE⊥AD于E,∴∠AEG=∠AEB=90°,
∴∠AGB=∠ABG,∴AG=AB=6,GE=BE,
∵AC=14,∴CG=8,
∵∠AGB=∠C+∠CBG,
∴∠ABC=∠ABG+∠CBG=∠AGB+∠CBG=∠C+2∠CBG,
∵∠ABC=3∠C,∴3∠C=∠C+2∠CBG,
∴∠C=∠CBG,∴BG=CG=8,∴BE=BG=4;
故本题答案为:4。
15.14
【解析】把AB、CD、EF分别向两方延长,交于点G、H、P,如图所示:
∵∠BAF=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,
∠BAF+∠ABC+∠BCD+∠CDE+∠DEF+∠EFA=(6 2)×180°=720°,
∴∠BAF=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=120°,
∴∠PAF=∠GBC=∠GCB=∠HDE=∠DEH=∠PFA=60°,
∴△APF、△BCG、△DEH是等边三角形,
∴∠P=∠G=∠H=60°,AF=PA,BC=BG=CG,DE=DH,
∴△PGH是等边三角形,∴PG=GH,即PA+AB+BG=CG+CD+DH,
∴AF+AB+BC=BC+CD+DE,
∵AB+BC=11,AF CD=3,,∴BC+DE=AB+BC+(AF CD)=3+11=14;
故本题答案为:14。
16.
【解析】∵AD=3BD,∴设BD=x,则AD=3x,∴AB=4x,
∵△ABC是等边三角形,∴AB=AC=BC=4x,∠A=∠ABC=60°,
∵AB∥EG,∴∠A=∠G=60°,∴∠ABC=∠G=60°,
∵∠ACE=∠ADC,∴∠BDC=∠GCE,
在△BCD和△GEC中,
∴△BCD≌△GEC(AAS),∴BD=GC=x,BC=GE=AB,
∴AG=AC+CG=5x,
在△ABF和△GEF中,
∴△ABF≌△GEF(AAS),∴AF=FG=x,
∴FC=x,∴=;
故本题答案为:。
17.①②④⑤
【解析】∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,∴∠ACD=∠BCE,
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS),∴AD=BE,结论①正确;
∵△ACD≌△BCE,∴∠CAD=∠CBE,
又∵∠ACB=∠DCE=60°,
∴∠BCD=180° 60° 60°=60°,
∴∠ACP=∠BCQ=60°,
在△ACP和△BCQ中,
∴△ACP≌△BCQ(AAS),∴AP=BQ,CP=CQ,
又∵∠PCQ=60°,∴△PCQ为等边三角形,结论④正确;
∴∠PQC=60°=∠DCE,∴PQ∥AE,结论②正确;
∵△ACD≌△BCE,∴∠ADC=∠AEO,
∴∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60°,∴结论⑤正确;
没有条件证出OP=OQ,③错误;
故本题答案为:①②④⑤。
18.①②③④
【解析】①连接OB,如图1,
∵△ABC中高AD恰好平分边BC,即AD是BC垂直平分线,
∴AB=AC,BD=CD,∴OB=OC=OP,
∴∠APO=∠ABO,∠DBO=∠DCO,
∵∠ABC=∠ABO+∠DBO=30°,
∴∠APO+∠DCO=30°,故①正确;
②在△OBP中,∠BOP=180° ∠OPB ∠OBP,
在△BOC中,∠BOC=180° ∠OBC ∠OCB,
∴∠POC=360° ∠BOP ∠BOC
=∠OPB+∠OBP+∠OBC+∠OCB
=(∠OPB+∠OCB)+(∠OBP+∠OBC)
=30°+∠ABD=30°+30°=60°,
∵PO=OC,∴△OPC是等边三角形,故②正确;
③如图2,在AC上截取AE=PA,
∵∠PAE=180° ∠BAC=60°,∴△APE是等边三角形,
∴∠PEA=∠APE=60°,PE=PA,∴∠APO+∠OPE=60°,
∵∠OPE+∠CPE=∠CPO=60°,∴∠APO=∠EPC,
在△OPA和△CPE中,
∴△OPA≌△CPE(SAS),∴AO=EC,
∴AC=AE+EC=AP+AO,故③正确;
④如图3,作CH⊥BP,
∵CH⊥BP,∠PHC=90°=∠ODC,
∵∠B=30°,∴∠HCB=60°=∠PCO,
∴∠HCB ∠HCO=∠PCO ∠HCO,即∠OCD=∠PCH,
在△CDO和△CHP中,
∴△CDO≌△CHP(AAS),∴S△OCD=S△CHP∴CH=CD,
∵CD=BD,∴BD=CH,
在Rt△ABD和Rt△ACH中,
∴Rt△ABD≌Rt△ACH(HL),∴S△ABD=S△AHC,
∵四边形OAPC面积=S△OAC+S△AHC+S△CHP=S△AOC+S△ABD+S△OCD=S△ABC,
∴四边形OAPC面积=S△ABC.故④正确;
故本题答案为:①②③④。
三、解答题
19.解:(1)∵AD垂直平分BE,EF垂直平分AC,
∴AB=AE=EC,
∴∠C=∠CAE,
∵∠BAE=40°,
∴∠AED=70°,
∴∠C=12∠AED=35°;
(2)∵△ABC周长20cm,AC=8cm,
∴AB+BE+EC=12cm,
即2DE+2EC=12cm,
∴DE+EC=DC=6cm。
20.证明:如图,过点A作AF∥BC,交BD的延长线于点F,
∴∠F=∠DBC,∠FAD=∠C,
∵∠ABC=2∠C,BD平分∠ABC,
∴∠ABD=∠DBC=∠C,
∴BD=CD,∠F=∠FAD=∠ABD,
∴AD=FD,AB=AF,
∵AE⊥BD,∴BE=EF=BF,
∵AC=AD+CD=FD+BD=BF,∴AC=2BE。
21.(1)要使△PBQ是等边三角形,即可得:PB=BQ,
在Rt△ABC中,∠C=90°,∠A=30°,BC=12cm.∴AB=2BC=24cm,
∵动点P以2cm/s,Q以1cm/s的速度出发,
∴BP=AB AP=(24 2t)cm,BQ=t cm,
即24 2t=t,解得:t=8,
故答案为:8;
(2)当t为6s或s时,△PBQ是直角三角形,理由如下:
∵∠C=90°,∠A=30°,BC=12cm,∴AB=2BC=24cm,
∵动点P以2cm/s,Q以1cm/s的速度出发,
∴BP=AB AP=(24 2t)cm,BQ=t cm,
∵△PBQ是直角三角形,
∴BP=2BQ或BQ=2BP,
当BP=2BQ时,24 2t=2t,解得t=6;
当BQ=2BP时,t=2(24 2t),解得t=;
所以,当t为6s或s时,△PBQ是直角三角形。
22.(1)解:∵∠A=60°,∴∠ABC+∠ACB=180° ∠A=120°,
∵BE平分∠ABC,CF平分∠ACB,
∴∠ABE=∠CBE=∠ABC,∠BCF=∠ACF=∠ACB,
∴∠CBE+∠BCF=∠ABC+∠ACB=×120°=60°,
∴∠BPC=180° (∠CBE+∠BCF)=180° 60°=120°;
(2)证明:在BC上截取BQ=BF,连接PQ,
在△FBP和△QBP中,
∴△FBP≌△QBP(SAS),∴FP=QP,∠BFP=∠BQP,
∵∠A=60°,∠FPE=∠BPC=120°,
∴∠AFP+∠AEP=360° 60° 120°=180°,∴∠BFP+∠CEP=180°,
∵∠CQP+∠BQP=180°,∴∠CEP=∠CQP,
在△CQP和△CEP中,
∴△CQP≌△CEP(AAS),∴QP=EP=FP,
∴△EFP是等腰三角形。
23.(1)解:如图1中,
∵∠ACE是△ABC的一个外角,∴∠BAC=∠ACE ∠ABC,
∵CO是∠ACE的角平分线,∴∠OCE=∠ACE,
∵OB是∠ABC的角平分线,∴∠OBE=∠ABC,
∴∠BAC=∠ACE ∠ABC=2∠OCE 2∠OBE=2(∠OCE ∠OBE)=2∠O=50°;
(2)证明:如图2中,过点O作OM⊥BD于点M,ON⊥AC于点N,OT⊥BE于点T.
∵CO平分∠ACE,ON⊥AC,OT⊥CE,∴ON=OT,
∵BO平分∠DBE,OM⊥BD,OT⊥BE,∴OM=OT,
∴OM=ON,∴AO平分∠CAD.
(3)解:∵S△BOC= BC OT=16,BC=4,∴OT=8,
∴OM=ON=OT=8,
∴S△ABC=S△△BOC+S△AOB S△AOC
=16+×6×8 ×5×8
=16+24 20
=20。
24.(1)证明:如图1,
∵BF⊥AD,∴∠AFB=90°,
∵∠ACB=90°,∴∠BCE=∠ACD=90°,
∵∠ADC=∠BDF,∴∠CAD=∠CBE,
在△ACD和△BCE中
∴△ACD≌△BCE(ASA),∴BE=AD;
(2)解:如图2,分别延长BF,AC交于点E,
由(1)知:BE=AD=5,
∵AD平分∠BAC,AF⊥BE,
∴∠ABF=∠E,∴AB=AE,
∴BF=BE=;
(3)解:AC+CD=AM,理由如下:
如图3,分别延长BF,AC交于点E,
由(1)可得△ACD≌△BCE,∴CD=CE,
∵BF⊥AD,∴∠AFE=∠AFM=90°,
∵AF平分∠EAM,∴∠EAF=∠MAF,
∴∠M=∠E,∴AM=AE=AC+CE,
∴AC+CD=AM。
25.(1)如图1,过点M作BC边的垂线交CA延长线于点F,
∴∠FMC=90°,∴∠FMA+∠AMC=90°,
∵将线段AM绕点M顺时针旋转90°,得到线段ME,
∴∠AME=90°,∴∠CME+∠AMC=90°,
∴∠FMA=∠CME,
∵∠BAC=90°,AB=AC,∴∠ABC=∠ACB=45°,
∴在Rt△FMC中,∠F=∠FCM=45°,∴FM=CM,
在△FMA和△CME中,
∴△FMA≌△CME(SAS),∴∠MCE=∠F=45°;
(2)AC CE=CM,理由如下:
如图2,过点M作BC边的垂线交CA于点F,
∴∠FMC=90°,∴∠FME+∠EMC=90°,
∵将线段AM绕点M顺时针旋转90°,得到线段ME,
∴∠AME=90°,∴∠FME+∠AMF=90°,∴∠FMA=∠CME,
在Rt△FMC中,∠F=∠FCM=45°,∴FM=CM,
在△FMA和△CME中,
∴△FMA≌△CMA(SAS),∴AF=CE,
在Rt△CMF中,CF=CM,
∴AC CE=AC AF=CF=CM。
26.解:(1)BM、NC、MN之间的数量关系BM+NC=MN,
∵DM=DN,∠MDN=60°,∴△MDN是等边三角形,
∵△ABC是等边三角形,∴∠A=60°,
∵BD=CD,∠BDC=120°,∴∠BDC=∠DCB=30°,∴∠MBD=∠NCD=90°,
在Rt△BDM和Rt△CDN中,
∴Rt△BDM≌Rt△CDN(HL),∴∠BDM=∠CDN=30°,BM=CN,
∴DM=2BM,DN=2CN,
∵△MDN是等边三角形,∴MN=DM=DN,
∴MN=2BM=2CN=BM+CN,
故答案为:BM+NC=MN;
(2)猜想:结论仍然成立,理由如下:
在CN的延长线上截取CM1=BM,连接DM1,
∵∠MBD=∠NCD=90°,∴∠MBD=∠M1CD=90°,
在△DBM和△DCM1中,
∴△DBM≌△DCM1(SAS),∴DM=DM1,∠MDB=∠M1DC,
∵∠MDN=60°,∠BDC=120°,∴∠MDB+∠CDN=60°,
∴∠M1DC+∠CDN=60°,即∠M1DN=60°=∠MDN,
在△MDN和△M1DN中,
∴△MDN≌△M1DN(SAS),∴MN=M1N=M1C+NC=BM+NC;
(3)证明:在CN上截取CM1=BM,连接DM1、MN,
由(2)得,△DBM≌△DCM1,∴DM=DM1,∠MDB=∠M1DC,
∵∠MDN=60°,∠BDC=120°,∴∠MDB+∠BDN=60°,
∴∠M1DC+∠BDN=60°,∴∠M1DN=60°=∠MDN,
在△MDN和△M1DN中,
∴△MDN≌△M1DN(SAS),∴MN=M1N=NC CM1=NC BM。
一、选择题(本题共10小题,每小题3分,共30分。)
1.室内墙壁上挂一平面镜,小明在平面镜内看到他背后墙上时钟的示数如图所示,则这时的实际时间应是( )
A.3:20 B.3:40 C.4:40 D.8:20
2.下列说法中:①关于某直线成轴对称的两个图形一定能完全重合;②线段是轴对称图形;③有一条公共边的两个全等三角形一定关于公共边所在直线对称;④关于某条直线对称的两个图形一定分别位于该直线的两侧.正确有( )
A.1个 B.2个 C.3个 D.4个
3.如图,射线AB与射线CD平行,点F在射线AB上,∠DCF=70°,AF=a(a为常数,且a>0),P为射线CD上的一动点(不包括端点C),将△CPF沿PF翻折得到△EPF,连接AE,则AE最大时,∠DPE的度数为( )
A.30° B.55° C.70° D.90°
4.如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE.如果∠A=α,∠DEA=β,∠CEA'=γ,∠BDA'=θ,那么下列式子中不一定成立的是( )
A.θ=2α+γ B.θ+α+γ=180° C.90+=β D.a+β=90°+
5.如图,AB∥CD,AD∥BC,AD⊥CD,点E为线段BC上一点,将线段AB沿AE折叠,点B的对应点F落在四边形ABCD外侧,连接EF,若AF∥BD,∠ADB=α,则∠DAE为( )
A.α B.90° 2α C.45°+ D.45°
6.如图,△ABC的两条内角平分线相交于点D,过点D作一条平分△ABC面积的直线,那么这条直线分成的两个图形的周长比是( )
A.2:1 B.1:1 C.2:3 D.3:1
7.如图,在△ABC中.AB=AC.BC=4,△ABC的面积是24,AC的垂直平分线EF分别交AC,AB边于点E,F,若点D为BC边的中点,点M为线段EF上一动点,连接CM,DM,则CM+DM的最小值为( )
A.6 B.10 C.12 D.13
8.如图所示,∠AOB=60°,点P是∠AOB内一定点,并且OP=2,点M、N分别是射线OA,OB上异于点O的动点,当△PMN的周长取最小值时,点O到线段MN的距离为( )
A.1 B.2 C.4 D.1.5
9.在等边△ABC中,D、E分别为AB、AC边上的动点,BD=2AE,连接DE,以DE为边在△ABC内作等边△DEF,连接CF,当D从点A向B运动(不运动到点B)时,∠ECF大小的变化情况是( )
A.不变 B.变小 C.先变大 D.先变大后变小
10.如图,在△ABC中,∠BAC和∠ABC的平分线AE,BF相交于点O,AE交BC于E,BF交AC于F,过点O作OD⊥BC于D,下列三个结论:①∠AOB=90°+∠C;②当∠C=60°时,AF+BE=AB;③若OD=a,AB+BC+CA=2b,则S△ABC=ab.其中正确的是( )
A.①② B.②③ C.①②③ D.①③
二、填空题(本题共8小题,每小题3分,共24分。)
11.墙上有一个数字式电子钟,在对面墙上的镜子里看到该电子钟显示的时间如图所示,那么它的实际时间是_____.
12.如图,直线L为线段AB的垂直平分线,交AB于M,在直线L上取一点C1,使得MC1=MB,得到第一个三角形ABC1;在射线MC1上取一点C2,使得C1C2=BC1;得到第二个三角形△ABC2;在射线MC1上取一点C3,使得C2C3=BC2,得到第三个三角形△ABC3…依次这样作下去,则第2022个三角形△ABC2022中∠AC2022B的度数为_____.
13.如图,在Rt△ABC中,∠A=90°,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=2,则BC的长为_____.
14.如图,在△ABC中,AD平分∠BAC,交BC于点D,BE⊥AD于E,AB=6,AC=14,∠ABC=3∠C.则BE=_____.
15.如图,六边形ABCDEF中,∠A=∠B=∠C=∠D=∠E=∠F,且AB+BC=11,FA CD=3,则BC+DE=_____.
16.如图,△ABC是等边三角形,点D在AB上,AD=3BD,∠ACE=∠ADC,CE=CD.G是AC延长线上一点,EG∥AB.连接BE交AC于点F,则的值为_____.
17.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:
①AD=BE;②PQ∥AE;③OP=OQ;④△CPQ为等边三角形;⑤∠AOB=60°.其中正确的有_____.(注:把你认为正确的答案序号都写上)
18.如图,已知△ABC中高AD恰好平分边BC,∠B=30°,点P是BA延长线上一点,点
O是线段AD上一点且OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP.其中正确的为_____.(填序号)
三、解答题(本题共8小题,共66分。)
19.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
(1)若∠BAE=40°,求∠C的度数;
(2)若△ABC周长为20cm,AC=8cm,求DC长.
20.如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,交AC于D,AE⊥BD,垂足为E.求证:AC=2BE.
21.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=12cm.动点P从点A出发,沿AB向点B运动,动点Q从点B出发,沿BC向点C运动,如果动点P以2cm/s,Q以1cm/s的速度同时出发,设运动时间为t(s),解答下列问题:
(1)t为多少时,△PBQ是等边三角形?
(2)P、Q在运动过程中,△PBQ的形状不断发生变化,当t为多少时,△PBQ是直角三角形?请说明理由.
22.如图,在△ABC中,∠A=60°.BE,CF交于点P,且分别平分∠ABC,∠ACB.
(1)求∠BPC的度数;
(2)连接EF,求证:△EFP是等腰三角形.
23.已知OB,OC分别是△ABC的内角∠ABC和外角∠ACE的角平分线.
(1)在图1中,已知∠O=25°,求∠BAC的度数.
(2)连接OA,如图2,证明OA是外角∠CAD的角平分线.
(3)在图2中,已知S△BOC=16,BC=4,AC=5,AB=6,直接写出△ABC的面积.
24.△ABC中,∠ACB=90°,AC=BC,点D是BC边上的一个动点,连接AD,过点B作BF⊥AD于点F.
(1)如图1,分别延长AC,BF相交于点E,求证:BE=AD;
(2)如图2,若AD平分∠BAC,AD=5,求BF的长;
(3)如图3,M是FB延长线上一点,AD平分∠MAC,试探究AC,CD,AM之间的数量关系并说明理由.
25.已知:在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC边中点.点M为线段BC上的一个动点(不与点C,点D重合),连接AM,将线段AM绕点M顺时针旋转90°,得到线段ME,连接EC.
(1)如图1,若点M在线段BD上,求∠MCE的度数.
(2)如图2,若点M在线段CD上,试探究线段AC、CE、CM之间的数量关系,并证明你的结论.
26.在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系.
(1)如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是_____;
(2)如图2,点M、N在边AB、AC上,且当DM≠DN时,猜想(1)问的结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.
(3)如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.
答案
一、选择题
1.B
【解析】根据镜面对称的性质,分析可得题中所显示的时刻与3:40呈轴对称,所以此时的实际时间为3:40;
故本题选B。
2.B
【解析】①关于某直线成轴对称的两个图形一定能完全重合,正确;
②线段是轴对称图形,正确;
③有一条公共边的两个全等三角形不一定关于公共边所在的直线对称,错误;
④关于某条直线对称的两个图形不一定分别位于该直线的两侧,错误;
所以正确的个数是2个;
故本题选B。
3.C
【解析】∵CD∥AB,∠DCF=70°,∴∠DCF=∠CFA=70°,
由折叠性质知,EF=CF,
∵CF的长度为定值,∴当点E在AB上时,点E到点A的距离最大,如图,
由折叠知,∠PEF=∠DCF=70°,
∵CD∥AB,∴∠DPB=∠PEF=70°;
故本题选C。
4.B
【解析】如图,
∵∠A=∠A'=α,∴θ=∠A+∠DFA=∠A+∠A′+γ=2α+γ,
故A选项成立,不符合题意;
∵∠DEA=∠DEA′=β,∴∠DEA+∠DEA′ ∠FEA′=180°,
即2β γ=180°,∴90°+=β,
故C选项成立,不符合题意;
∵∠FDE=∠ADE,θ+∠FDE+∠ADE=180°,∴∠FDE=,
∵α+β=θ+∠FDE,∴α+β=θ+,即α+β=90°+,
故D选项成立,不符合题意;
故本题选B。
5.D
【解析】设∠DAE=x,
∵AB∥CD,AD⊥CD,∴AB⊥AD,∴∠BAD=90°,
∴∠BAE=∠BAD ∠DAE=90° x,
由折叠的性质得:∠FAE=∠BAE=90° x,
∴∠FAD=∠FAE ∠DAE=90° 2x,
∵AF∥BD,∴∠FAD=∠ADB=α,∴90° 2x=α,
解得:x=45° ,即∠DAE=45° ;
故本题选D。
6.B
【解析】连接AD,过D点作DE⊥AB于点E,作DF⊥AC于点F,作DG⊥BC于点G,
∵△ABC的两条内角平分线相交于点D,∴DE=DF=DG,
设MN平分△ABC的面积,则S△BDM+S△BDN=S△ADM+S△ADC+S△DCN,
∵S△BDM=BM DE,S△ADM=AM DE,S△ADC=AC DF,S△DCN=NC DG,S△BDN=BN DG,
∴BM DE+BN DG=AM DE+AC DF+NC DG,
∴BM+BN=AM+AC+NC,
∴BM+BN+MN=AM+AC+NC+MN,
即这条直线分成的两个图形的周长比是1:1;
故本题选B。
7.C
【解析】解:连接AD,
∵△ABC是等腰三角形,点D是BC边的中点.
∴AD⊥BC,∴S△ABC=BC AD=×4×AD=24,解得AD=12,
∵EF是线段AB的垂直平分线,
∴点C关于直线EF的对称点为点A,
连接AM,则CM+DM=AM+DM≥AD,
∴当点M在线段AD上时,CM+DM的值最小,
∴AD的长为CM+MD的最小值;
故本题选C。
8.A
【解析】分别作点P关于OB和OA的对称点P'和P'',连接OP'、OP''、P'P'',则P'P''与OB的交点为点N',P'P''与OA的交点为点M',
连接PN'、PM',则此时P'P''的值即为△PMN的周长的最小值,过点O作OC⊥P'P''于点C,如图所示:
由对称性可知OP=OP'=OP'',
∵∠AOB=60°,∴∠P'OP''=2×60°=120°,
∴∠OP'P''=∠OP''P'=30°,
∵OP=2,OC⊥P'P'',∴OC=OP'=1;
故本题选A。
9.A
【解析】在AC上截取CN=AE,连接FN,如图所示:
∵△ABC是等边三角形,∴∠A=60°,AB=AC,
∵BD=2AE,∴AD=NE,
∵△DEF是等边三角形,
∴DE=EF,∠DEF=60°,
∵∠ADE=180° ∠A ∠AED=180° 60° ∠AED=120° ∠AED,
∠NEF=180° ∠DEF ∠AED=180° 60° ∠AED=120° ∠AED,
∴∠ADE=∠NEF,
在△ADE和△NEF中,
∴△ADE≌△NEF(SAS),∴AE=FN,∠FNE=∠A=60°,
∴FN=CN,∴∠NCF=∠NFC,
∵∠FNE=∠NCF+∠NFC=60°,∴∠NCF=30°,即∠ECF=30°;
故本题选A。
10.C
【解析】∵∠BAC和∠ABC的平分线相交于点O,
∴∠OBA=∠CBA,∠OAB=∠CAB,
∴∠AOB=180° ∠OBA ∠OAB=180° ∠CBA ∠CAB
=180° (180° ∠C)=90°+∠C,故①正确;
∵∠C=60°,由①知:∠AOB=90°+∠C,∴∠AOB=120°,
∴∠AOF=60°,∴∠BOE=60°,
如图,在AB上取一点H,使BH=BE,
∵BF是∠ABC的角平分线,∴∠HBO=∠EBO,
在△HBO和△EBO中,
∴△HBO≌△EBO(SAS),∴∠BOH=∠BOE=60°,
∴∠AOH=180° 60° 60°=60°,∴∠AOH=∠AOF,
∵AE是∠BAC的角平分线,∴∠HAO=∠FAO,
在△HAO和△FAO中,
∴△HAO≌△FAO(ASA),∴AF=AH,
∴AB=BH+AH=BE+AF,故②正确;
作OH⊥AC于H,OM⊥AB于M,
∵∠BAC和∠ABC的平分线相交于点O,∴OH=OM=OD=a,
∵AB+AC+BC=2b,
∴S△ABC=×AB×OM+×AC×OH+×BC×OD=(AB+AC+BC) a=ab,
故③正确;
故本题选C。
二、填空题
11.12:51
【解析】根据镜面对称的性质,分析可得题中所显示的图片与12:51成轴对称,所以此时实际时刻为12:51;
故本题答案为:12:51。
12.
【解析】由于直线L为线段AB的垂直平分线,
∴C1A=C1B,C2A=C2B,C3A=C3B,…
∵C1C2=BC1,∴C1C2=BC1=AC1,
∴∠C1C2A=∠C1AC2=∠AC1M,∠C1C2B=∠C1BC2=∠BC1M,
∴∠AC2B=∠AC1B,
同理,∴∠AC3B=∠AC2B=×∠AC1B,
∴∠AC4B=∠AC3B=××∠AC1B,
∴∠AC5B=∠AC4B=×××∠AC1B,
…
∴∠AC2022B=()2021∠AC1B=;
故本题答案为:。
13.12
【解析】∵CM平分∠ACB,MN平分∠AMC,∴∠ACM=∠BCM,∠AMN=∠CMN,
∵MN∥BC,∴∠AMN=∠CMN=∠ACM=∠BCM,∴MN=CN,
∵∠A=90°,∴∠AMN=∠CMN=∠ACM=∠BCM=30°,
∵AN=2,∴MN=CN=4,∴AC=6,
∵MN∥BC,∴∠B=∠AMN=30°,∴BC=2AC=12;
故本题答案为:12。
14.4
【解析】延长BE交AC于G,
∵AD平分∠BAC,∴∠GAE=∠BAE,
∵BE⊥AD于E,∴∠AEG=∠AEB=90°,
∴∠AGB=∠ABG,∴AG=AB=6,GE=BE,
∵AC=14,∴CG=8,
∵∠AGB=∠C+∠CBG,
∴∠ABC=∠ABG+∠CBG=∠AGB+∠CBG=∠C+2∠CBG,
∵∠ABC=3∠C,∴3∠C=∠C+2∠CBG,
∴∠C=∠CBG,∴BG=CG=8,∴BE=BG=4;
故本题答案为:4。
15.14
【解析】把AB、CD、EF分别向两方延长,交于点G、H、P,如图所示:
∵∠BAF=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,
∠BAF+∠ABC+∠BCD+∠CDE+∠DEF+∠EFA=(6 2)×180°=720°,
∴∠BAF=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=120°,
∴∠PAF=∠GBC=∠GCB=∠HDE=∠DEH=∠PFA=60°,
∴△APF、△BCG、△DEH是等边三角形,
∴∠P=∠G=∠H=60°,AF=PA,BC=BG=CG,DE=DH,
∴△PGH是等边三角形,∴PG=GH,即PA+AB+BG=CG+CD+DH,
∴AF+AB+BC=BC+CD+DE,
∵AB+BC=11,AF CD=3,,∴BC+DE=AB+BC+(AF CD)=3+11=14;
故本题答案为:14。
16.
【解析】∵AD=3BD,∴设BD=x,则AD=3x,∴AB=4x,
∵△ABC是等边三角形,∴AB=AC=BC=4x,∠A=∠ABC=60°,
∵AB∥EG,∴∠A=∠G=60°,∴∠ABC=∠G=60°,
∵∠ACE=∠ADC,∴∠BDC=∠GCE,
在△BCD和△GEC中,
∴△BCD≌△GEC(AAS),∴BD=GC=x,BC=GE=AB,
∴AG=AC+CG=5x,
在△ABF和△GEF中,
∴△ABF≌△GEF(AAS),∴AF=FG=x,
∴FC=x,∴=;
故本题答案为:。
17.①②④⑤
【解析】∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,∴∠ACD=∠BCE,
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS),∴AD=BE,结论①正确;
∵△ACD≌△BCE,∴∠CAD=∠CBE,
又∵∠ACB=∠DCE=60°,
∴∠BCD=180° 60° 60°=60°,
∴∠ACP=∠BCQ=60°,
在△ACP和△BCQ中,
∴△ACP≌△BCQ(AAS),∴AP=BQ,CP=CQ,
又∵∠PCQ=60°,∴△PCQ为等边三角形,结论④正确;
∴∠PQC=60°=∠DCE,∴PQ∥AE,结论②正确;
∵△ACD≌△BCE,∴∠ADC=∠AEO,
∴∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60°,∴结论⑤正确;
没有条件证出OP=OQ,③错误;
故本题答案为:①②④⑤。
18.①②③④
【解析】①连接OB,如图1,
∵△ABC中高AD恰好平分边BC,即AD是BC垂直平分线,
∴AB=AC,BD=CD,∴OB=OC=OP,
∴∠APO=∠ABO,∠DBO=∠DCO,
∵∠ABC=∠ABO+∠DBO=30°,
∴∠APO+∠DCO=30°,故①正确;
②在△OBP中,∠BOP=180° ∠OPB ∠OBP,
在△BOC中,∠BOC=180° ∠OBC ∠OCB,
∴∠POC=360° ∠BOP ∠BOC
=∠OPB+∠OBP+∠OBC+∠OCB
=(∠OPB+∠OCB)+(∠OBP+∠OBC)
=30°+∠ABD=30°+30°=60°,
∵PO=OC,∴△OPC是等边三角形,故②正确;
③如图2,在AC上截取AE=PA,
∵∠PAE=180° ∠BAC=60°,∴△APE是等边三角形,
∴∠PEA=∠APE=60°,PE=PA,∴∠APO+∠OPE=60°,
∵∠OPE+∠CPE=∠CPO=60°,∴∠APO=∠EPC,
在△OPA和△CPE中,
∴△OPA≌△CPE(SAS),∴AO=EC,
∴AC=AE+EC=AP+AO,故③正确;
④如图3,作CH⊥BP,
∵CH⊥BP,∠PHC=90°=∠ODC,
∵∠B=30°,∴∠HCB=60°=∠PCO,
∴∠HCB ∠HCO=∠PCO ∠HCO,即∠OCD=∠PCH,
在△CDO和△CHP中,
∴△CDO≌△CHP(AAS),∴S△OCD=S△CHP∴CH=CD,
∵CD=BD,∴BD=CH,
在Rt△ABD和Rt△ACH中,
∴Rt△ABD≌Rt△ACH(HL),∴S△ABD=S△AHC,
∵四边形OAPC面积=S△OAC+S△AHC+S△CHP=S△AOC+S△ABD+S△OCD=S△ABC,
∴四边形OAPC面积=S△ABC.故④正确;
故本题答案为:①②③④。
三、解答题
19.解:(1)∵AD垂直平分BE,EF垂直平分AC,
∴AB=AE=EC,
∴∠C=∠CAE,
∵∠BAE=40°,
∴∠AED=70°,
∴∠C=12∠AED=35°;
(2)∵△ABC周长20cm,AC=8cm,
∴AB+BE+EC=12cm,
即2DE+2EC=12cm,
∴DE+EC=DC=6cm。
20.证明:如图,过点A作AF∥BC,交BD的延长线于点F,
∴∠F=∠DBC,∠FAD=∠C,
∵∠ABC=2∠C,BD平分∠ABC,
∴∠ABD=∠DBC=∠C,
∴BD=CD,∠F=∠FAD=∠ABD,
∴AD=FD,AB=AF,
∵AE⊥BD,∴BE=EF=BF,
∵AC=AD+CD=FD+BD=BF,∴AC=2BE。
21.(1)要使△PBQ是等边三角形,即可得:PB=BQ,
在Rt△ABC中,∠C=90°,∠A=30°,BC=12cm.∴AB=2BC=24cm,
∵动点P以2cm/s,Q以1cm/s的速度出发,
∴BP=AB AP=(24 2t)cm,BQ=t cm,
即24 2t=t,解得:t=8,
故答案为:8;
(2)当t为6s或s时,△PBQ是直角三角形,理由如下:
∵∠C=90°,∠A=30°,BC=12cm,∴AB=2BC=24cm,
∵动点P以2cm/s,Q以1cm/s的速度出发,
∴BP=AB AP=(24 2t)cm,BQ=t cm,
∵△PBQ是直角三角形,
∴BP=2BQ或BQ=2BP,
当BP=2BQ时,24 2t=2t,解得t=6;
当BQ=2BP时,t=2(24 2t),解得t=;
所以,当t为6s或s时,△PBQ是直角三角形。
22.(1)解:∵∠A=60°,∴∠ABC+∠ACB=180° ∠A=120°,
∵BE平分∠ABC,CF平分∠ACB,
∴∠ABE=∠CBE=∠ABC,∠BCF=∠ACF=∠ACB,
∴∠CBE+∠BCF=∠ABC+∠ACB=×120°=60°,
∴∠BPC=180° (∠CBE+∠BCF)=180° 60°=120°;
(2)证明:在BC上截取BQ=BF,连接PQ,
在△FBP和△QBP中,
∴△FBP≌△QBP(SAS),∴FP=QP,∠BFP=∠BQP,
∵∠A=60°,∠FPE=∠BPC=120°,
∴∠AFP+∠AEP=360° 60° 120°=180°,∴∠BFP+∠CEP=180°,
∵∠CQP+∠BQP=180°,∴∠CEP=∠CQP,
在△CQP和△CEP中,
∴△CQP≌△CEP(AAS),∴QP=EP=FP,
∴△EFP是等腰三角形。
23.(1)解:如图1中,
∵∠ACE是△ABC的一个外角,∴∠BAC=∠ACE ∠ABC,
∵CO是∠ACE的角平分线,∴∠OCE=∠ACE,
∵OB是∠ABC的角平分线,∴∠OBE=∠ABC,
∴∠BAC=∠ACE ∠ABC=2∠OCE 2∠OBE=2(∠OCE ∠OBE)=2∠O=50°;
(2)证明:如图2中,过点O作OM⊥BD于点M,ON⊥AC于点N,OT⊥BE于点T.
∵CO平分∠ACE,ON⊥AC,OT⊥CE,∴ON=OT,
∵BO平分∠DBE,OM⊥BD,OT⊥BE,∴OM=OT,
∴OM=ON,∴AO平分∠CAD.
(3)解:∵S△BOC= BC OT=16,BC=4,∴OT=8,
∴OM=ON=OT=8,
∴S△ABC=S△△BOC+S△AOB S△AOC
=16+×6×8 ×5×8
=16+24 20
=20。
24.(1)证明:如图1,
∵BF⊥AD,∴∠AFB=90°,
∵∠ACB=90°,∴∠BCE=∠ACD=90°,
∵∠ADC=∠BDF,∴∠CAD=∠CBE,
在△ACD和△BCE中
∴△ACD≌△BCE(ASA),∴BE=AD;
(2)解:如图2,分别延长BF,AC交于点E,
由(1)知:BE=AD=5,
∵AD平分∠BAC,AF⊥BE,
∴∠ABF=∠E,∴AB=AE,
∴BF=BE=;
(3)解:AC+CD=AM,理由如下:
如图3,分别延长BF,AC交于点E,
由(1)可得△ACD≌△BCE,∴CD=CE,
∵BF⊥AD,∴∠AFE=∠AFM=90°,
∵AF平分∠EAM,∴∠EAF=∠MAF,
∴∠M=∠E,∴AM=AE=AC+CE,
∴AC+CD=AM。
25.(1)如图1,过点M作BC边的垂线交CA延长线于点F,
∴∠FMC=90°,∴∠FMA+∠AMC=90°,
∵将线段AM绕点M顺时针旋转90°,得到线段ME,
∴∠AME=90°,∴∠CME+∠AMC=90°,
∴∠FMA=∠CME,
∵∠BAC=90°,AB=AC,∴∠ABC=∠ACB=45°,
∴在Rt△FMC中,∠F=∠FCM=45°,∴FM=CM,
在△FMA和△CME中,
∴△FMA≌△CME(SAS),∴∠MCE=∠F=45°;
(2)AC CE=CM,理由如下:
如图2,过点M作BC边的垂线交CA于点F,
∴∠FMC=90°,∴∠FME+∠EMC=90°,
∵将线段AM绕点M顺时针旋转90°,得到线段ME,
∴∠AME=90°,∴∠FME+∠AMF=90°,∴∠FMA=∠CME,
在Rt△FMC中,∠F=∠FCM=45°,∴FM=CM,
在△FMA和△CME中,
∴△FMA≌△CMA(SAS),∴AF=CE,
在Rt△CMF中,CF=CM,
∴AC CE=AC AF=CF=CM。
26.解:(1)BM、NC、MN之间的数量关系BM+NC=MN,
∵DM=DN,∠MDN=60°,∴△MDN是等边三角形,
∵△ABC是等边三角形,∴∠A=60°,
∵BD=CD,∠BDC=120°,∴∠BDC=∠DCB=30°,∴∠MBD=∠NCD=90°,
在Rt△BDM和Rt△CDN中,
∴Rt△BDM≌Rt△CDN(HL),∴∠BDM=∠CDN=30°,BM=CN,
∴DM=2BM,DN=2CN,
∵△MDN是等边三角形,∴MN=DM=DN,
∴MN=2BM=2CN=BM+CN,
故答案为:BM+NC=MN;
(2)猜想:结论仍然成立,理由如下:
在CN的延长线上截取CM1=BM,连接DM1,
∵∠MBD=∠NCD=90°,∴∠MBD=∠M1CD=90°,
在△DBM和△DCM1中,
∴△DBM≌△DCM1(SAS),∴DM=DM1,∠MDB=∠M1DC,
∵∠MDN=60°,∠BDC=120°,∴∠MDB+∠CDN=60°,
∴∠M1DC+∠CDN=60°,即∠M1DN=60°=∠MDN,
在△MDN和△M1DN中,
∴△MDN≌△M1DN(SAS),∴MN=M1N=M1C+NC=BM+NC;
(3)证明:在CN上截取CM1=BM,连接DM1、MN,
由(2)得,△DBM≌△DCM1,∴DM=DM1,∠MDB=∠M1DC,
∵∠MDN=60°,∠BDC=120°,∴∠MDB+∠BDN=60°,
∴∠M1DC+∠BDN=60°,∴∠M1DN=60°=∠MDN,
在△MDN和△M1DN中,
∴△MDN≌△M1DN(SAS),∴MN=M1N=NC CM1=NC BM。
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
