湘教版八年级下册(新)期末复习练习(五) 数据的频数分布
文档属性
| 名称 | 湘教版八年级下册(新)期末复习练习(五) 数据的频数分布 |  | |
| 格式 | zip | ||
| 文件大小 | 178.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-30 14:01:50 | ||
图片预览


文档简介
期末复习(五) 数据的频数分布
考点一 频数与频率
【例1】某单位有职工100名,按他们的年龄分成8组,在40~42(岁)组内有职工32名,那么这个小组的频率是( )
A.0.12 B.0.38 C.0.32 D.32
【分析】∵总人数为100人,在40~42(岁)组内有职工32名,∴这个小组的频率为32÷100=0.32.故选C.
【解答】C
【方法归纳】频率=频数÷总数.
变式练习
1.已知在一个样本中,40个数据分别落在4个组内,第一、二、四组数据个数分别为5、12、8,则第三组的频数为__________.
2.一次跳远比赛中,成绩在4.05米以上的人有8人,频率为0.4,则参加比赛的运动员共有( )
A.10人 B.20人 C.30人 D.40人
考点二 频数分布表
【例2】已知样本:8,6,10,13,1 ( http: / / www.21cnjy.com )0,8,7,10,11,12,10,8,9,11,9,12,10,12,11,9.在列频数分布表时,如果取组距为2,那么应分成__________组,9.5~11.5这一组的频率是__________.
【分析】对于样本的数据,最大值为13,最小 ( http: / / www.21cnjy.com )值为6,即极差是7,则组距=(13-6)÷2=3.5,即应分成4组,观察样本,知共有8个样本在9.5~11.5这一组中,故其频率为0.4.
【解答】4,0.4
【方法归纳】组距=(最大值-最小值)÷组数;频率的计算方法:频率=频数÷总数.
3.对某班40名同学的一次数学成绩进行统计 ( http: / / www.21cnjy.com ),在频数分布表中80.5~90.5这一组频数是0.20,那么成绩在80.5~90.5这个分数段的人数是( )
A.8 B.6 C.10 D.12
考点三 频数直方图
【例3】从斜桥中学八年级参加数学竞赛学生中随机抽取了30名学生的成绩,分数如下(单位:分):
90,85,84,86,87,98,79,85,90,93,
68,95,85,71,78,61,94,88,77,100,
70,97,85,99,88,68,85,92,93,97.
(1)求出这组数据中最大值与最小值的差;
(2)按组距7分将数据分组,列出频数分布表;
(3)在同一个坐标系中画出频数分布直方图(补全横坐标).
【分析】(1)在给出的数据中找出最大值与最小值作差即可;
(2)已知组距为7分,∴可以由组数=(最大值-最小值)÷组距+1,得出组距,可由此得出分数段,再由题中所给的分数列出频数分布表;
(3)由第二问中的频数分布表,可以画出频数分布直方图.
【解答】(1)这组数据中最大值与最小值的差为100-61=39;
(2)组数=39÷7+1≈6,
所以可得分数段为:58.5 ( http: / / www.21cnjy.com )~65.5,65.5~72.5,72.5~79.5,79.5~86.5,86.5~93.5,93.5~100.5,
可列出频数分布表,如下表:
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(3)由第二问中的频数分布表,可以画出频数分布直方图,如上图.
【方法归纳】本题考查了频数分布表和频数分布直方图的画法,在整理数据时要认真仔细.
4.某校八年级学生参加一次数学竞赛的成 ( http: / / www.21cnjy.com )绩如下(每组分数含最低分,不含最高分):60~70分的60人;70~80分的45人;80~90的25人;90~100分的20人.
(1)制作频数分布表;
(2)画出频数分布直方图.
复习测试
一、选择题(每小题3分,共30分)
1.数据1,2,0,1,1,2中,数据“1”出现的频数是( )
A.1 B.2 C.3 D.4
2.某校对1 200名女生的身高进行了测量,身高在1.58~1.63(单位:m),这一小组的频率为0.25,则该组的人数为( )
A.150人 B.300人 C.600人 D.900人
3.为了了解一批数据在各个范围内所占比例大小,将这批数据分组,落在各小组里的数据个数叫做( )
A.频率 B.样本容量 C.频数 D.频数累计
4.下列说法正确的是( )
A.频数越小,频率越大
B.频数大,频率也一定大
C.频数一定时,频率越小,总次数越大
D.频数很大时,频率可能超过1
5.对八年级某班45名同学的一次数 ( http: / / www.21cnjy.com )学单元测试成绩进行统计,如果频数分布直方图中80.5~90.5分这一组的频数是9,那么这个班的学生这次数学测试成绩在80.5~90.5分之间的频率是( )
A.0.2 B.0.25 C.0.3 D.0.4
6.已知数据35,31,33,35,37,3 ( http: / / www.21cnjy.com )9,35,38,40,39,36,34,35,37,36,32,34,35,36,34,在列频数分布表时,如果取组距为2,那么应分成的组数为( )
A.4 B.5 C.6 D.7
7.已知数据25,28,30,27,29,31,33,36,35,32,26,29,31,30,28,那么频率为0.2的范围是( )
A.25~27 B.28~30 C.31~33 D.34~36
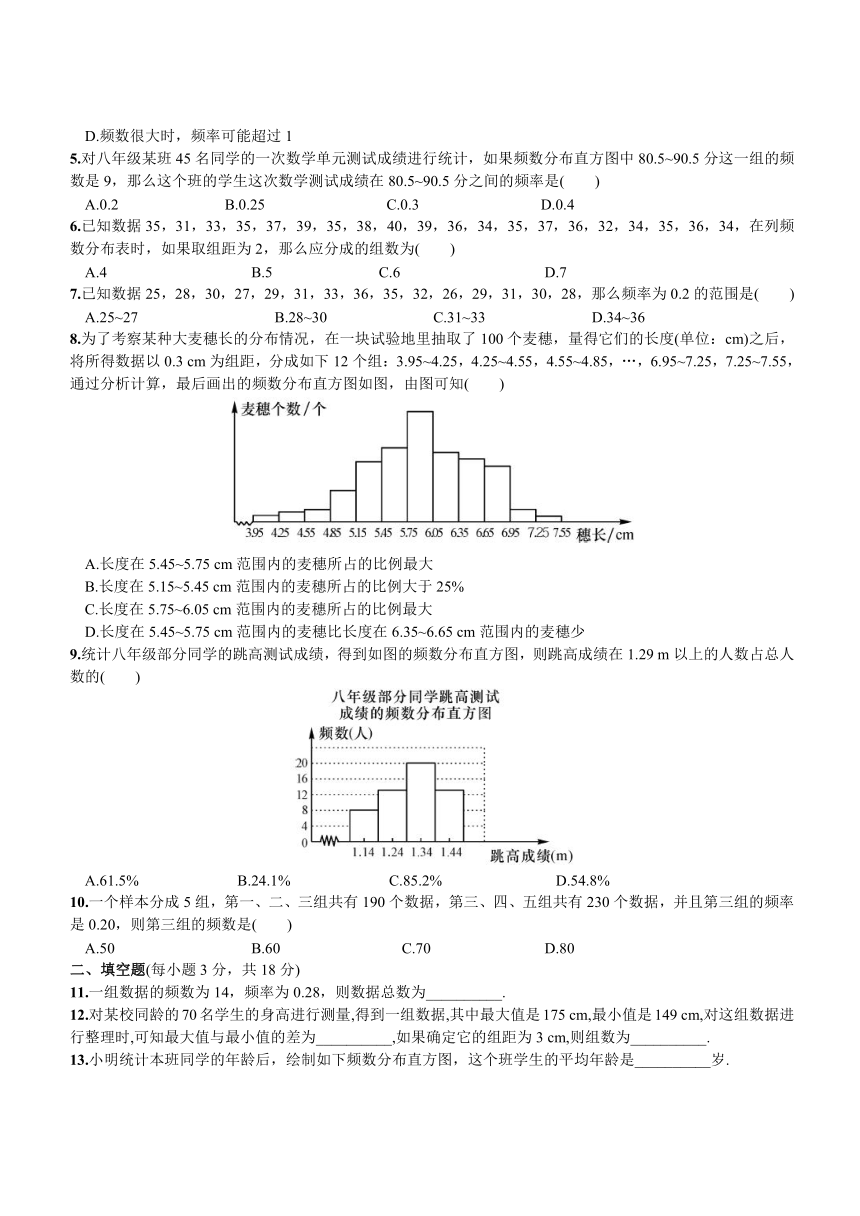
8.为了考察某种大麦穗长 ( http: / / www.21cnjy.com )的分布情况,在一块试验地里抽取了100个麦穗,量得它们的长度(单位:cm)之后,将所得数据以0.3 cm为组距,分成如下12个组:3.95~4.25,4.25~4.55,4.55~4.85,…,6.95~7.25,7.25~7.55,通过分析计算,最后画出的频数分布直方图如图,由图可知( )
( http: / / www.21cnjy.com )
A.长度在5.45~5.75 cm范围内的麦穗所占的比例最大
B.长度在5.15~5.45 cm范围内的麦穗所占的比例大于25%
C.长度在5.75~6.05 cm范围内的麦穗所占的比例最大
D.长度在5.45~5.75 cm范围内的麦穗比长度在6.35~6.65 cm范围内的麦穗少
9.统计八年级部分同学的跳高测试成绩,得到如图的频数分布直方图,则跳高成绩在1.29 m以上的人数占总人数的( )
( http: / / www.21cnjy.com )
A.61.5% B.24.1% C.85.2% D.54.8%
10.一个样本分成5组,第一、二、三组 ( http: / / www.21cnjy.com )共有190个数据,第三、四、五组共有230个数据,并且第三组的频率是0.20,则第三组的频数是( )
A.50 B.60 C.70 D.80
二、填空题(每小题3分,共18分)
11.一组数据的频数为14,频率为0.28,则数据总数为__________.
12.对某校同龄的70名学生的身高 ( http: / / www.21cnjy.com )进行测量,得到一组数据,其中最大值是175 cm,最小值是149 cm,对这组数据进行整理时,可知最大值与最小值的差为__________,如果确定它的组距为3 cm,则组数为__________.
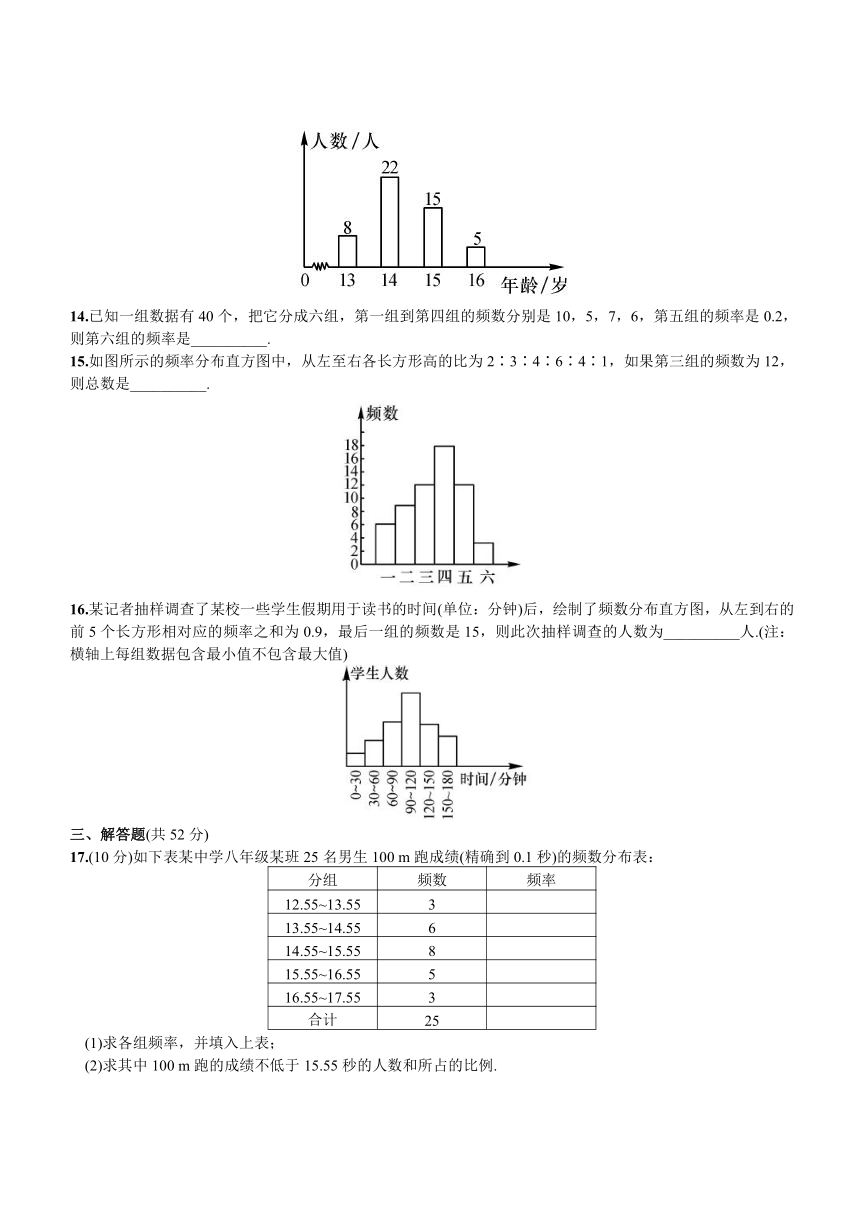
13.小明统计本班同学的年龄后,绘制如下频数分布直方图,这个班学生的平均年龄是__________岁.
( http: / / www.21cnjy.com )
14.已知一组数据有40个,把它分成六组 ( http: / / www.21cnjy.com ),第一组到第四组的频数分别是10,5,7,6,第五组的频率是0.2,则第六组的频率是__________.
15.如图所示的频率分布直方图中,从左至右各长方形高的比为2∶3∶4∶6∶4∶1,如果第三组的频数为12,则总数是__________.
( http: / / www.21cnjy.com )
16.某记者抽样调查了某校一些学生假 ( http: / / www.21cnjy.com )期用于读书的时间(单位:分钟)后,绘制了频数分布直方图,从左到右的前5个长方形相对应的频率之和为0.9,最后一组的频数是15,则此次抽样调查的人数为__________人.(注:横轴上每组数据包含最小值不包含最大值)
( http: / / www.21cnjy.com )
三、解答题(共52分)
17.(10分)如下表某中学八年级某班25名男生100 m跑成绩(精确到0.1秒)的频数分布表:
分组 频数 频率
12.55~13.55 3
13.55~14.55 6
14.55~15.55 8
15.55~16.55 5
16.55~17.55 3
合计 25
(1)求各组频率,并填入上表;
(2)求其中100 m跑的成绩不低于15.55秒的人数和所占的比例.
18.(10分)某地区为了增强市民的法 ( http: / / www.21cnjy.com )制观念,抽调了一部分市民进行一次知识竞赛,竞赛成绩(得分取整数)进行整理后分成五组并绘制成频数分布直方图,如图所示,请结合图提供的信息,解答下列问题:
( http: / / www.21cnjy.com )
(1)抽取了多少人参加竞赛
(2)60.5~70.5这一分数段的频数、频率分别是多少
(3)这次竞赛成绩的中位数落在哪个分数段内
19.(10分)下图是某班学生一次数学考试成绩的频数分布直方图,其中纵坐标表示学生数,观察图形,回答下列问题:
( http: / / www.21cnjy.com )
(1)全班有多少学生
(2)此次考试的平均成绩大概是多少
(3)不及格的人数有多少 占全班多大比例
(4)如果80分以上的成绩算优良,那么获优良成绩的学生占全班多大比例
20.(10分)为创建“国家园 ( http: / / www.21cnjy.com )林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图.
根据以上信息,解答下列问题:
( http: / / www.21cnjy.com )
(1)请补全频数分布直方图;
(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?
(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?
21.(12分)设中学生体质健康综合评 ( http: / / www.21cnjy.com )定成绩为x分,满分为100分.规定:85≤x≤100为A级,75≤x<85为B级,60≤x<75为C级,x<60为D级.现随机抽取福海中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图.请根据图中的信息,解答下列问题:
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1)在这次调查中,一共抽取了__________名学生,a=__________%;
(2)补全条形统计图;
(3)扇形统计图中C级对应的圆心角为__________度;
(4)若该校共有2 000名学生,请你估计该校D级学生有多少名?
参考答案
变式练习
1.15 2.B 3.A
4.(1)频数分布表:
(2)频数分布直方图:
( http: / / www.21cnjy.com )
复习测试
1.C 2.B 3.C 4.C 5.A 6.B 7.A 8.C 9.A 10.C
11.50 12.26 cm 9 13.14.3 14.0.1 15.60 16.150
17.(1)0.12 0.24 0.32 0.2 0.12 1
(2)观察图表可得:有8人100 m跑的成绩不低于15.55秒,所占的比例为8÷25=0.32.
18.(1)48人.
(2)12,0.25.
(3)70.5~80.5.
19.(1)观察直方图可知:成绩在29~39分间的学生有1人,39~49分间的有2人,…,
因此,全班共有学生人数是1+2+3+8+10+14+6=44(人).
(2)由于直方图只反映每个分数区间有多少学生,未反映这些学生每位成绩具体是多少,故不能由图算出平均数,但如果采用某种适当的方式则可算出近似平均数.下面我们采用每个区间左端点数加6.作为该区间每位学生的成绩计算:=(35×1+45×2+55×3+65×8+75×10+85×14+95×6)=×3320≈75.5(分).
(3)因60分以下为不及格,其中29~39间有1人,39~49间有2人,49~59间有3人,
故不及格人数有1+2+3=6(人).
占全班人数的比例是:6÷44≈13.6%.
(4)获优良成绩的学生人数有:14+6=20(人),
占全班比例是:20÷44≈45.5%.
20.(1)200-(35+40+70+10)=45,补全频数分布直方图图略.
(2)设抽了x人,则=,解得x=8.
(3)依题意知获一等奖的人数为200×25%=50(人).
则一等奖的分数线是80分.
21.(1)∵24÷48%=50,a=×100%=24%,
∴在这次调查中,一共抽取了50名学生,a=24%;
(2)补全条形统计图略.
(3)∵360°×(×100%)=72°,扇形统计图中C级对应的圆心角为72度;
(4)∵2 000×(×100%)=160(名).
∴若该校共有2 000名学生,估计该校D级学生有160名.
考点一 频数与频率
【例1】某单位有职工100名,按他们的年龄分成8组,在40~42(岁)组内有职工32名,那么这个小组的频率是( )
A.0.12 B.0.38 C.0.32 D.32
【分析】∵总人数为100人,在40~42(岁)组内有职工32名,∴这个小组的频率为32÷100=0.32.故选C.
【解答】C
【方法归纳】频率=频数÷总数.
变式练习
1.已知在一个样本中,40个数据分别落在4个组内,第一、二、四组数据个数分别为5、12、8,则第三组的频数为__________.
2.一次跳远比赛中,成绩在4.05米以上的人有8人,频率为0.4,则参加比赛的运动员共有( )
A.10人 B.20人 C.30人 D.40人
考点二 频数分布表
【例2】已知样本:8,6,10,13,1 ( http: / / www.21cnjy.com )0,8,7,10,11,12,10,8,9,11,9,12,10,12,11,9.在列频数分布表时,如果取组距为2,那么应分成__________组,9.5~11.5这一组的频率是__________.
【分析】对于样本的数据,最大值为13,最小 ( http: / / www.21cnjy.com )值为6,即极差是7,则组距=(13-6)÷2=3.5,即应分成4组,观察样本,知共有8个样本在9.5~11.5这一组中,故其频率为0.4.
【解答】4,0.4
【方法归纳】组距=(最大值-最小值)÷组数;频率的计算方法:频率=频数÷总数.
3.对某班40名同学的一次数学成绩进行统计 ( http: / / www.21cnjy.com ),在频数分布表中80.5~90.5这一组频数是0.20,那么成绩在80.5~90.5这个分数段的人数是( )
A.8 B.6 C.10 D.12
考点三 频数直方图
【例3】从斜桥中学八年级参加数学竞赛学生中随机抽取了30名学生的成绩,分数如下(单位:分):
90,85,84,86,87,98,79,85,90,93,
68,95,85,71,78,61,94,88,77,100,
70,97,85,99,88,68,85,92,93,97.
(1)求出这组数据中最大值与最小值的差;
(2)按组距7分将数据分组,列出频数分布表;
(3)在同一个坐标系中画出频数分布直方图(补全横坐标).
【分析】(1)在给出的数据中找出最大值与最小值作差即可;
(2)已知组距为7分,∴可以由组数=(最大值-最小值)÷组距+1,得出组距,可由此得出分数段,再由题中所给的分数列出频数分布表;
(3)由第二问中的频数分布表,可以画出频数分布直方图.
【解答】(1)这组数据中最大值与最小值的差为100-61=39;
(2)组数=39÷7+1≈6,
所以可得分数段为:58.5 ( http: / / www.21cnjy.com )~65.5,65.5~72.5,72.5~79.5,79.5~86.5,86.5~93.5,93.5~100.5,
可列出频数分布表,如下表:
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(3)由第二问中的频数分布表,可以画出频数分布直方图,如上图.
【方法归纳】本题考查了频数分布表和频数分布直方图的画法,在整理数据时要认真仔细.
4.某校八年级学生参加一次数学竞赛的成 ( http: / / www.21cnjy.com )绩如下(每组分数含最低分,不含最高分):60~70分的60人;70~80分的45人;80~90的25人;90~100分的20人.
(1)制作频数分布表;
(2)画出频数分布直方图.
复习测试
一、选择题(每小题3分,共30分)
1.数据1,2,0,1,1,2中,数据“1”出现的频数是( )
A.1 B.2 C.3 D.4
2.某校对1 200名女生的身高进行了测量,身高在1.58~1.63(单位:m),这一小组的频率为0.25,则该组的人数为( )
A.150人 B.300人 C.600人 D.900人
3.为了了解一批数据在各个范围内所占比例大小,将这批数据分组,落在各小组里的数据个数叫做( )
A.频率 B.样本容量 C.频数 D.频数累计
4.下列说法正确的是( )
A.频数越小,频率越大
B.频数大,频率也一定大
C.频数一定时,频率越小,总次数越大
D.频数很大时,频率可能超过1
5.对八年级某班45名同学的一次数 ( http: / / www.21cnjy.com )学单元测试成绩进行统计,如果频数分布直方图中80.5~90.5分这一组的频数是9,那么这个班的学生这次数学测试成绩在80.5~90.5分之间的频率是( )
A.0.2 B.0.25 C.0.3 D.0.4
6.已知数据35,31,33,35,37,3 ( http: / / www.21cnjy.com )9,35,38,40,39,36,34,35,37,36,32,34,35,36,34,在列频数分布表时,如果取组距为2,那么应分成的组数为( )
A.4 B.5 C.6 D.7
7.已知数据25,28,30,27,29,31,33,36,35,32,26,29,31,30,28,那么频率为0.2的范围是( )
A.25~27 B.28~30 C.31~33 D.34~36
8.为了考察某种大麦穗长 ( http: / / www.21cnjy.com )的分布情况,在一块试验地里抽取了100个麦穗,量得它们的长度(单位:cm)之后,将所得数据以0.3 cm为组距,分成如下12个组:3.95~4.25,4.25~4.55,4.55~4.85,…,6.95~7.25,7.25~7.55,通过分析计算,最后画出的频数分布直方图如图,由图可知( )
( http: / / www.21cnjy.com )
A.长度在5.45~5.75 cm范围内的麦穗所占的比例最大
B.长度在5.15~5.45 cm范围内的麦穗所占的比例大于25%
C.长度在5.75~6.05 cm范围内的麦穗所占的比例最大
D.长度在5.45~5.75 cm范围内的麦穗比长度在6.35~6.65 cm范围内的麦穗少
9.统计八年级部分同学的跳高测试成绩,得到如图的频数分布直方图,则跳高成绩在1.29 m以上的人数占总人数的( )
( http: / / www.21cnjy.com )
A.61.5% B.24.1% C.85.2% D.54.8%
10.一个样本分成5组,第一、二、三组 ( http: / / www.21cnjy.com )共有190个数据,第三、四、五组共有230个数据,并且第三组的频率是0.20,则第三组的频数是( )
A.50 B.60 C.70 D.80
二、填空题(每小题3分,共18分)
11.一组数据的频数为14,频率为0.28,则数据总数为__________.
12.对某校同龄的70名学生的身高 ( http: / / www.21cnjy.com )进行测量,得到一组数据,其中最大值是175 cm,最小值是149 cm,对这组数据进行整理时,可知最大值与最小值的差为__________,如果确定它的组距为3 cm,则组数为__________.
13.小明统计本班同学的年龄后,绘制如下频数分布直方图,这个班学生的平均年龄是__________岁.
( http: / / www.21cnjy.com )
14.已知一组数据有40个,把它分成六组 ( http: / / www.21cnjy.com ),第一组到第四组的频数分别是10,5,7,6,第五组的频率是0.2,则第六组的频率是__________.
15.如图所示的频率分布直方图中,从左至右各长方形高的比为2∶3∶4∶6∶4∶1,如果第三组的频数为12,则总数是__________.
( http: / / www.21cnjy.com )
16.某记者抽样调查了某校一些学生假 ( http: / / www.21cnjy.com )期用于读书的时间(单位:分钟)后,绘制了频数分布直方图,从左到右的前5个长方形相对应的频率之和为0.9,最后一组的频数是15,则此次抽样调查的人数为__________人.(注:横轴上每组数据包含最小值不包含最大值)
( http: / / www.21cnjy.com )
三、解答题(共52分)
17.(10分)如下表某中学八年级某班25名男生100 m跑成绩(精确到0.1秒)的频数分布表:
分组 频数 频率
12.55~13.55 3
13.55~14.55 6
14.55~15.55 8
15.55~16.55 5
16.55~17.55 3
合计 25
(1)求各组频率,并填入上表;
(2)求其中100 m跑的成绩不低于15.55秒的人数和所占的比例.
18.(10分)某地区为了增强市民的法 ( http: / / www.21cnjy.com )制观念,抽调了一部分市民进行一次知识竞赛,竞赛成绩(得分取整数)进行整理后分成五组并绘制成频数分布直方图,如图所示,请结合图提供的信息,解答下列问题:
( http: / / www.21cnjy.com )
(1)抽取了多少人参加竞赛
(2)60.5~70.5这一分数段的频数、频率分别是多少
(3)这次竞赛成绩的中位数落在哪个分数段内
19.(10分)下图是某班学生一次数学考试成绩的频数分布直方图,其中纵坐标表示学生数,观察图形,回答下列问题:
( http: / / www.21cnjy.com )
(1)全班有多少学生
(2)此次考试的平均成绩大概是多少
(3)不及格的人数有多少 占全班多大比例
(4)如果80分以上的成绩算优良,那么获优良成绩的学生占全班多大比例
20.(10分)为创建“国家园 ( http: / / www.21cnjy.com )林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图.
根据以上信息,解答下列问题:
( http: / / www.21cnjy.com )
(1)请补全频数分布直方图;
(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?
(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?
21.(12分)设中学生体质健康综合评 ( http: / / www.21cnjy.com )定成绩为x分,满分为100分.规定:85≤x≤100为A级,75≤x<85为B级,60≤x<75为C级,x<60为D级.现随机抽取福海中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图.请根据图中的信息,解答下列问题:
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1)在这次调查中,一共抽取了__________名学生,a=__________%;
(2)补全条形统计图;
(3)扇形统计图中C级对应的圆心角为__________度;
(4)若该校共有2 000名学生,请你估计该校D级学生有多少名?
参考答案
变式练习
1.15 2.B 3.A
4.(1)频数分布表:
(2)频数分布直方图:
( http: / / www.21cnjy.com )
复习测试
1.C 2.B 3.C 4.C 5.A 6.B 7.A 8.C 9.A 10.C
11.50 12.26 cm 9 13.14.3 14.0.1 15.60 16.150
17.(1)0.12 0.24 0.32 0.2 0.12 1
(2)观察图表可得:有8人100 m跑的成绩不低于15.55秒,所占的比例为8÷25=0.32.
18.(1)48人.
(2)12,0.25.
(3)70.5~80.5.
19.(1)观察直方图可知:成绩在29~39分间的学生有1人,39~49分间的有2人,…,
因此,全班共有学生人数是1+2+3+8+10+14+6=44(人).
(2)由于直方图只反映每个分数区间有多少学生,未反映这些学生每位成绩具体是多少,故不能由图算出平均数,但如果采用某种适当的方式则可算出近似平均数.下面我们采用每个区间左端点数加6.作为该区间每位学生的成绩计算:=(35×1+45×2+55×3+65×8+75×10+85×14+95×6)=×3320≈75.5(分).
(3)因60分以下为不及格,其中29~39间有1人,39~49间有2人,49~59间有3人,
故不及格人数有1+2+3=6(人).
占全班人数的比例是:6÷44≈13.6%.
(4)获优良成绩的学生人数有:14+6=20(人),
占全班比例是:20÷44≈45.5%.
20.(1)200-(35+40+70+10)=45,补全频数分布直方图图略.
(2)设抽了x人,则=,解得x=8.
(3)依题意知获一等奖的人数为200×25%=50(人).
则一等奖的分数线是80分.
21.(1)∵24÷48%=50,a=×100%=24%,
∴在这次调查中,一共抽取了50名学生,a=24%;
(2)补全条形统计图略.
(3)∵360°×(×100%)=72°,扇形统计图中C级对应的圆心角为72度;
(4)∵2 000×(×100%)=160(名).
∴若该校共有2 000名学生,估计该校D级学生有160名.
同课章节目录
