湘教版八年级下册(新)第4章《一次函数》同步测试
文档属性
| 名称 | 湘教版八年级下册(新)第4章《一次函数》同步测试 |  | |
| 格式 | zip | ||
| 文件大小 | 87.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-30 13:44:53 | ||
图片预览

文档简介
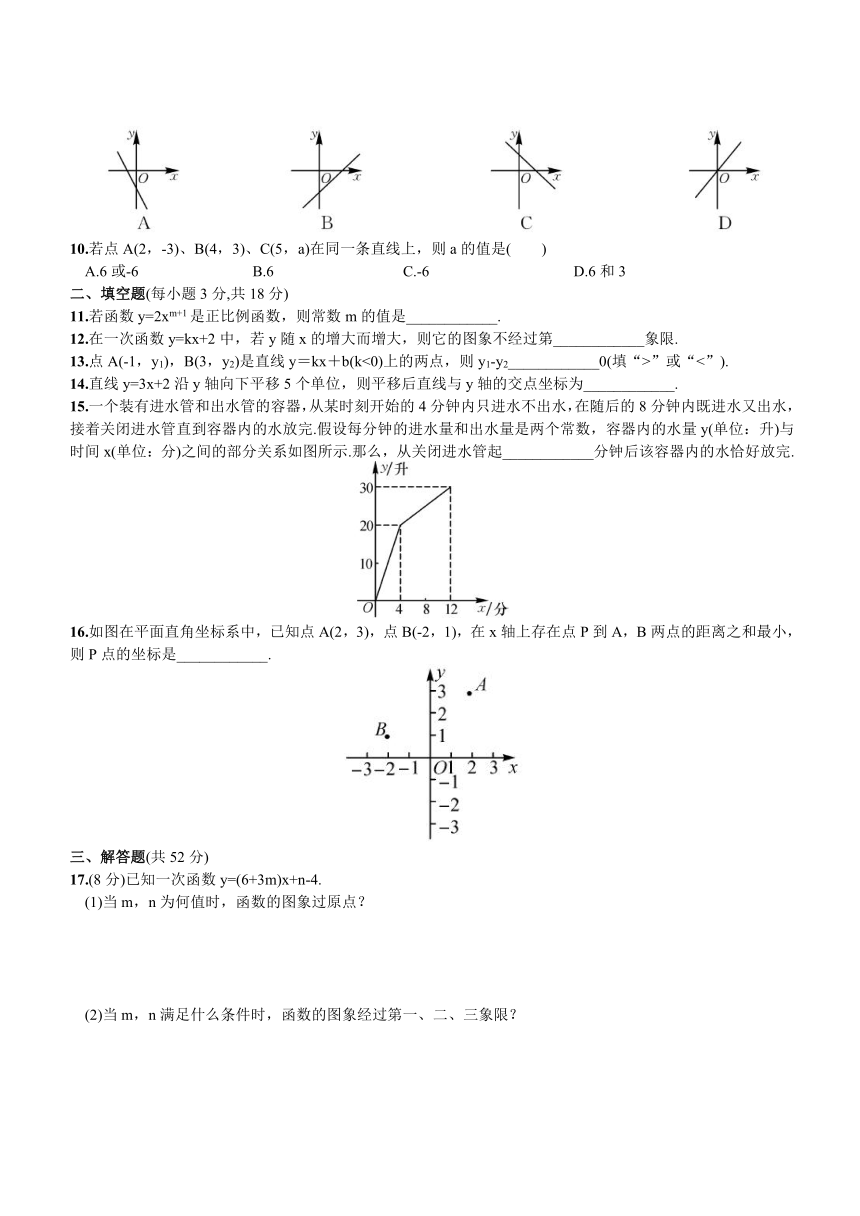
第4章 一次函数
(时间:45分钟 满分:100分)
一、选择题(每小题3分,共30分)
1.下列函数:①y=-2x;②y=x2+1;③y=-0.5x-1.其中是一次函数的个数有( )
A.0个 B.1个 C.2个 D.3个
2.若正比例函数y=kx的图象经过点(1,2),则k的值为( )
A.- B.-2 C. D.2
3.若一次函数y=(2-m)x-2的函数值y随x的增大而减小,则m的取值范围是( )
A.m<0 B.m>0 C.m<2 D.m>2
4.(2014·东营)直线y=-x+1经过的象限是( )
A.第一、二、三象限 B.第一、二、四象限
C.第二、三、四象限 D.第一、三、四象限
5.若点A(2,4)在函数y=kx-2的图象上,则下列各点在此函数图象上的是( )
A.(1,1) B.(-1,1) C.(-2,-2) D.(2,-2)
6.李大爷要围成一个矩形菜园,菜园的一边利 ( http: / / www.21cnjy.com )用足够长的墙,用篱笆围成的另外三边总长应恰好为24米,要围成的菜园是如图所示的矩形ABCD,设BC的边长为x米,AB边的长为y米,则y与x之间的函数关系式是( )
A.y=-2x+24(0<x<12) B.y=-x+12(0<x<24)
C.y=2x-24(0<x<12) D.y=x-12(0<x<24)
( http: / / www.21cnjy.com )
7.某航空公司规定,旅客乘 ( http: / / www.21cnjy.com )机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量是( )
A.20 kg B.25 kg C.28 kg D.30 kg
( http: / / www.21cnjy.com )
8.直线y=-x+3与x轴、y轴所围成的三角形的面积为( )
A.3 B.6 C. D.
9.关于x的一次函数y=kx+k2+1的图象可能正确的是( )
( http: / / www.21cnjy.com )
10.若点A(2,-3)、B(4,3)、C(5,a)在同一条直线上,则a的值是( )
A.6或-6 B.6 C.-6 D.6和3
二、填空题(每小题3分,共18分)
11.若函数y=2xm+1是正比例函数,则常数m的值是____________.
12.在一次函数y=kx+2中,若y随x的增大而增大,则它的图象不经过第____________象限.
13.点A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上的两点,则y1-y2____________0(填“>”或“<”).
14.直线y=3x+2沿y轴向下平移5个单位,则平移后直线与y轴的交点坐标为____________.
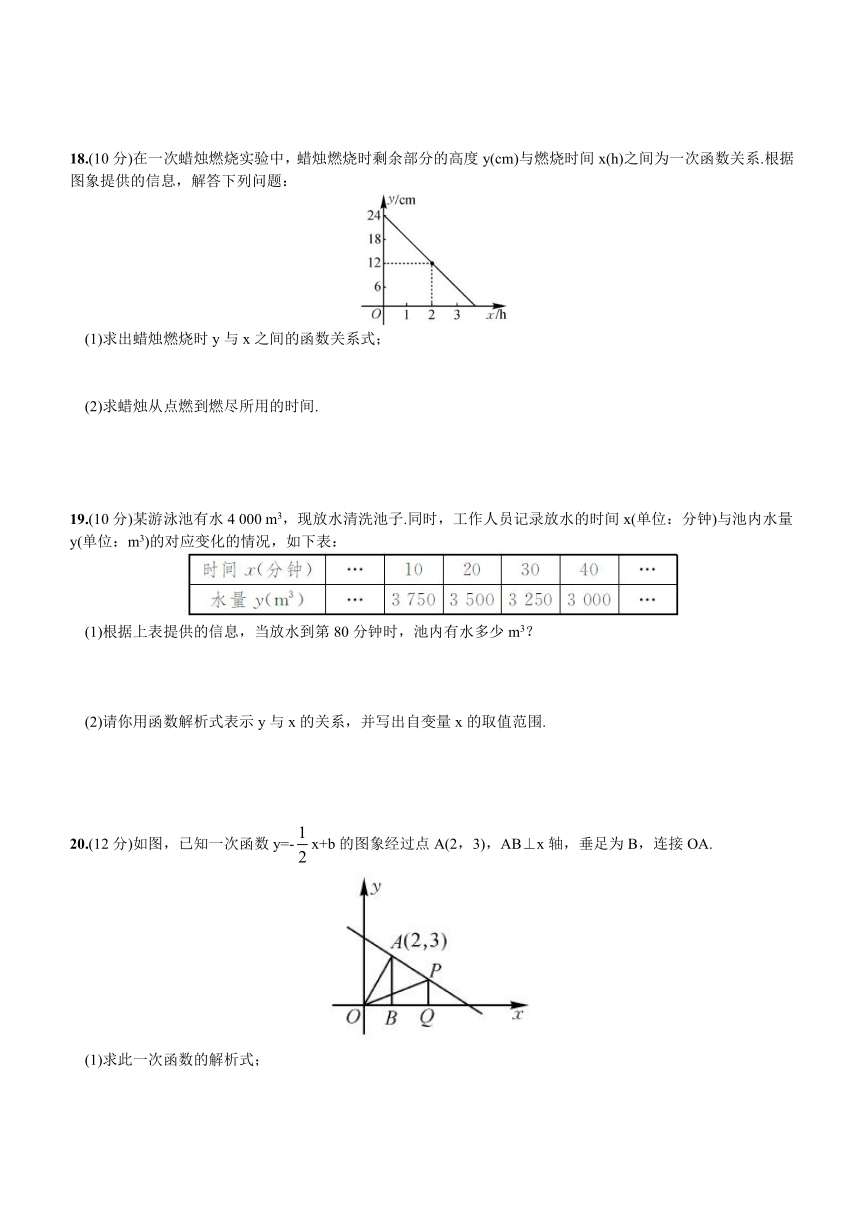
15.一个装有进水管和出水管的容器 ( http: / / www.21cnjy.com ),从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的部分关系如图所示.那么,从关闭进水管起____________分钟后该容器内的水恰好放完.
( http: / / www.21cnjy.com )
16.如图在平面直角坐标系中,已知点A(2, ( http: / / www.21cnjy.com )3),点B(-2,1),在x轴上存在点P到A,B两点的距离之和最小,则P点的坐标是____________.
( http: / / www.21cnjy.com )
三、解答题(共52分)
17.(8分)已知一次函数y=(6+3m)x+n-4.
(1)当m,n为何值时,函数的图象过原点?
(2)当m,n满足什么条件时,函数的图象经过第一、二、三象限?
18.(10分)在一次蜡烛 ( http: / / www.21cnjy.com )燃烧实验中,蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间为一次函数关系.根据图象提供的信息,解答下列问题:
( http: / / www.21cnjy.com )
(1)求出蜡烛燃烧时y与x之间的函数关系式;
(2)求蜡烛从点燃到燃尽所用的时间.
19.(10分)某游泳池 ( http: / / www.21cnjy.com )有水4 000 m3,现放水清洗池子.同时,工作人员记录放水的时间x(单位:分钟)与池内水量y(单位:m3)的对应变化的情况,如下表:
(1)根据上表提供的信息,当放水到第80分钟时,池内有水多少m3?
(2)请你用函数解析式表示y与x的关系,并写出自变量x的取值范围.
20.(12分)如图,已知一次函数y=-x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA.
( http: / / www.21cnjy.com )
(1)求此一次函数的解析式;
(2)设点P为直线y=-x+b上的一点,且在第一象限内,经过P作x轴的垂线,垂足为Q.若点P的横坐标为5,求S△POQ与S△AOB的比值.
21.(12分)已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离d可用公式d=计算.
例如:求点P(-2,1)到直线y=x+1的距离.
解:因为直线y=x+1可变形为x-y+1=0,其中k=1,b=1,
所以点P(-2,1)到直线y=x+1的距离为:d====.
根据以上材料,求:
(1)点P(1,1)到直线y=3x-2的距离,并说明点P与直线的位置关系;
(2)点P(2,-1)到直线y=2x-1的距离;
(3)已知直线y=-x+1与y=-x+3平行,求这两条直线的距离.
参考答案
1.C 2.D 3.D 4.B 5.A 6.B 7.A 8.A 9.C 10.B
11.0 12.四 13.> 14.(0,-3) 15.8 16.(-1,0)
17.(1)∵一次函数y=(6+3m)x+n-4的图象过原点,
∴6+3m≠0,且n-4=0.解得m≠-2,n=4.
(2)∵该函数的图象经过第一、二、三象限,
∴6+3m>0,且n-4>0.解得m>-2,n>4.
18.(1)设y=kx+b,过(0,24),(2,12),
∴解得
∴y=-6x+24;
(2)当y=0,0=-6x+24,解得x=4.
∴蜡烛从点燃到燃尽所用的时间为4小时.
19.(1)由图表可知,每10分钟放水250 m3,所以,第80分钟时,池内有水4 000-8×250=2 000(m3);
(2)设函数关系式为y=kx+b,
∵x=20时,y=3 500,x=40时,y=3 000,
∴解得
∴y=-25x+4 000(0≤x≤160).
20.(1)∵一次函数y=-x+b的图象经过点A(2,3),
∴3=(-)×2+b.解得b=4.
故此一次函数的解析式为:y=-x+4.
(2)∵点P在直线y=-x+4的图象上,
∴当x=5时,y=-×5+4=,即P(5,).
∴S△POQ=×OQ·PQ=×5×=.
又∵A(2,3),
∴S△AOB=×OB·AB=×2×3=3.
∴==.
即S△POQ与S△AOB的比值为.
21.(1)因为直线y=3x-2可变形为3x-y-2=0,其中k=3,b=-2,
所以点P(1,1)到直线y=3x-2的距离为:d===0.
这时点P在直线上;
(2)因为直线y=2x-1可变形为2x-y-1=0,其中k=2,b=-1,
所以点P(2,-1)到直线y=2x-1的距离为:d====;
(3)∵直线y=-x+1、y=-x+3平行,
∴任取直线y=-x+1上的一点到直线y=-x+3的距离即为两直线之间的距离.
∴取y=-x+1上的一点P(0,1)到直线y=-x+3的距离.
d====.
即两直线之间的距离为.
(时间:45分钟 满分:100分)
一、选择题(每小题3分,共30分)
1.下列函数:①y=-2x;②y=x2+1;③y=-0.5x-1.其中是一次函数的个数有( )
A.0个 B.1个 C.2个 D.3个
2.若正比例函数y=kx的图象经过点(1,2),则k的值为( )
A.- B.-2 C. D.2
3.若一次函数y=(2-m)x-2的函数值y随x的增大而减小,则m的取值范围是( )
A.m<0 B.m>0 C.m<2 D.m>2
4.(2014·东营)直线y=-x+1经过的象限是( )
A.第一、二、三象限 B.第一、二、四象限
C.第二、三、四象限 D.第一、三、四象限
5.若点A(2,4)在函数y=kx-2的图象上,则下列各点在此函数图象上的是( )
A.(1,1) B.(-1,1) C.(-2,-2) D.(2,-2)
6.李大爷要围成一个矩形菜园,菜园的一边利 ( http: / / www.21cnjy.com )用足够长的墙,用篱笆围成的另外三边总长应恰好为24米,要围成的菜园是如图所示的矩形ABCD,设BC的边长为x米,AB边的长为y米,则y与x之间的函数关系式是( )
A.y=-2x+24(0<x<12) B.y=-x+12(0<x<24)
C.y=2x-24(0<x<12) D.y=x-12(0<x<24)
( http: / / www.21cnjy.com )
7.某航空公司规定,旅客乘 ( http: / / www.21cnjy.com )机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量是( )
A.20 kg B.25 kg C.28 kg D.30 kg
( http: / / www.21cnjy.com )
8.直线y=-x+3与x轴、y轴所围成的三角形的面积为( )
A.3 B.6 C. D.
9.关于x的一次函数y=kx+k2+1的图象可能正确的是( )
( http: / / www.21cnjy.com )
10.若点A(2,-3)、B(4,3)、C(5,a)在同一条直线上,则a的值是( )
A.6或-6 B.6 C.-6 D.6和3
二、填空题(每小题3分,共18分)
11.若函数y=2xm+1是正比例函数,则常数m的值是____________.
12.在一次函数y=kx+2中,若y随x的增大而增大,则它的图象不经过第____________象限.
13.点A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上的两点,则y1-y2____________0(填“>”或“<”).
14.直线y=3x+2沿y轴向下平移5个单位,则平移后直线与y轴的交点坐标为____________.
15.一个装有进水管和出水管的容器 ( http: / / www.21cnjy.com ),从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的部分关系如图所示.那么,从关闭进水管起____________分钟后该容器内的水恰好放完.
( http: / / www.21cnjy.com )
16.如图在平面直角坐标系中,已知点A(2, ( http: / / www.21cnjy.com )3),点B(-2,1),在x轴上存在点P到A,B两点的距离之和最小,则P点的坐标是____________.
( http: / / www.21cnjy.com )
三、解答题(共52分)
17.(8分)已知一次函数y=(6+3m)x+n-4.
(1)当m,n为何值时,函数的图象过原点?
(2)当m,n满足什么条件时,函数的图象经过第一、二、三象限?
18.(10分)在一次蜡烛 ( http: / / www.21cnjy.com )燃烧实验中,蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间为一次函数关系.根据图象提供的信息,解答下列问题:
( http: / / www.21cnjy.com )
(1)求出蜡烛燃烧时y与x之间的函数关系式;
(2)求蜡烛从点燃到燃尽所用的时间.
19.(10分)某游泳池 ( http: / / www.21cnjy.com )有水4 000 m3,现放水清洗池子.同时,工作人员记录放水的时间x(单位:分钟)与池内水量y(单位:m3)的对应变化的情况,如下表:
(1)根据上表提供的信息,当放水到第80分钟时,池内有水多少m3?
(2)请你用函数解析式表示y与x的关系,并写出自变量x的取值范围.
20.(12分)如图,已知一次函数y=-x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA.
( http: / / www.21cnjy.com )
(1)求此一次函数的解析式;
(2)设点P为直线y=-x+b上的一点,且在第一象限内,经过P作x轴的垂线,垂足为Q.若点P的横坐标为5,求S△POQ与S△AOB的比值.
21.(12分)已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离d可用公式d=计算.
例如:求点P(-2,1)到直线y=x+1的距离.
解:因为直线y=x+1可变形为x-y+1=0,其中k=1,b=1,
所以点P(-2,1)到直线y=x+1的距离为:d====.
根据以上材料,求:
(1)点P(1,1)到直线y=3x-2的距离,并说明点P与直线的位置关系;
(2)点P(2,-1)到直线y=2x-1的距离;
(3)已知直线y=-x+1与y=-x+3平行,求这两条直线的距离.
参考答案
1.C 2.D 3.D 4.B 5.A 6.B 7.A 8.A 9.C 10.B
11.0 12.四 13.> 14.(0,-3) 15.8 16.(-1,0)
17.(1)∵一次函数y=(6+3m)x+n-4的图象过原点,
∴6+3m≠0,且n-4=0.解得m≠-2,n=4.
(2)∵该函数的图象经过第一、二、三象限,
∴6+3m>0,且n-4>0.解得m>-2,n>4.
18.(1)设y=kx+b,过(0,24),(2,12),
∴解得
∴y=-6x+24;
(2)当y=0,0=-6x+24,解得x=4.
∴蜡烛从点燃到燃尽所用的时间为4小时.
19.(1)由图表可知,每10分钟放水250 m3,所以,第80分钟时,池内有水4 000-8×250=2 000(m3);
(2)设函数关系式为y=kx+b,
∵x=20时,y=3 500,x=40时,y=3 000,
∴解得
∴y=-25x+4 000(0≤x≤160).
20.(1)∵一次函数y=-x+b的图象经过点A(2,3),
∴3=(-)×2+b.解得b=4.
故此一次函数的解析式为:y=-x+4.
(2)∵点P在直线y=-x+4的图象上,
∴当x=5时,y=-×5+4=,即P(5,).
∴S△POQ=×OQ·PQ=×5×=.
又∵A(2,3),
∴S△AOB=×OB·AB=×2×3=3.
∴==.
即S△POQ与S△AOB的比值为.
21.(1)因为直线y=3x-2可变形为3x-y-2=0,其中k=3,b=-2,
所以点P(1,1)到直线y=3x-2的距离为:d===0.
这时点P在直线上;
(2)因为直线y=2x-1可变形为2x-y-1=0,其中k=2,b=-1,
所以点P(2,-1)到直线y=2x-1的距离为:d====;
(3)∵直线y=-x+1、y=-x+3平行,
∴任取直线y=-x+1上的一点到直线y=-x+3的距离即为两直线之间的距离.
∴取y=-x+1上的一点P(0,1)到直线y=-x+3的距离.
d====.
即两直线之间的距离为.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
