湘教版八年级下册(新)第4章《综合练习 一次函数的综合应用》同步练习
文档属性
| 名称 | 湘教版八年级下册(新)第4章《综合练习 一次函数的综合应用》同步练习 | 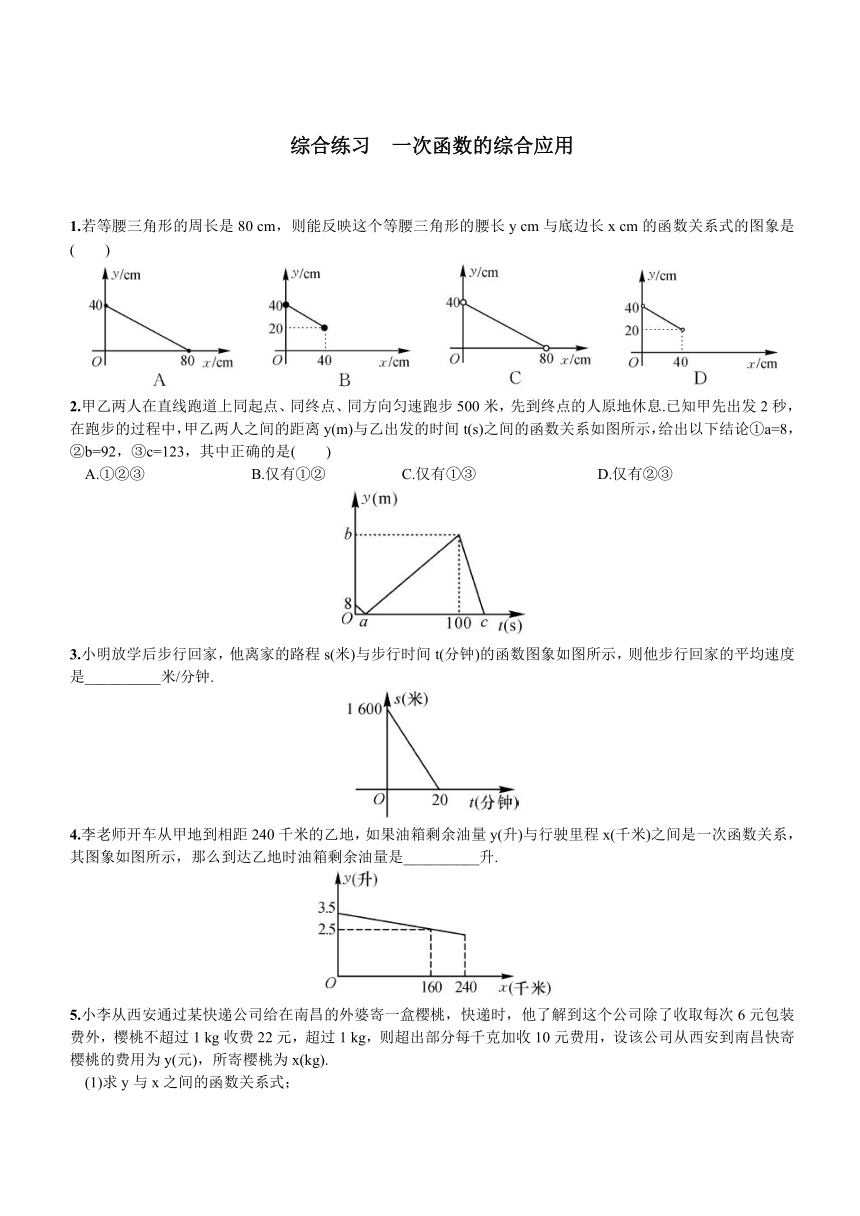 | |
| 格式 | zip | ||
| 文件大小 | 77.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-30 13:45:31 | ||
图片预览


文档简介
综合练习 一次函数的综合应用
1.若等腰三角形的周长是80 cm,则能反映这个等腰三角形的腰长y cm与底边长x cm的函数关系式的图象是( )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
2.甲乙两人在直线跑道上同起点、同终点、 ( http: / / www.21cnjy.com )同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒,在跑步的过程中,甲乙两人之间的距离y(m)与乙出发的时间t(s)之间的函数关系如图所示,给出以下结论①a=8,②b=92,③c=123,其中正确的是( )
A.①②③ B.仅有①② C.仅有①③ D.仅有②③
( http: / / www.21cnjy.com )
3.小明放学后步行回家,他离家的路程s(米)与步行时间t(分钟)的函数图象如图所示,则他步行回家的平均速度是__________米/分钟.
( http: / / www.21cnjy.com )
4.李老师开车从甲地到相距240千米的乙地 ( http: / / www.21cnjy.com ),如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图象如图所示,那么到达乙地时油箱剩余油量是__________升.
( http: / / www.21cnjy.com )
5.小李从西安通过某快递公司给在南昌的外婆 ( http: / / www.21cnjy.com )寄一盒樱桃,快递时,他了解到这个公司除了收取每次6元包装费外,樱桃不超过1 kg收费22元,超过1 kg,则超出部分每千克加收10元费用,设该公司从西安到南昌快寄樱桃的费用为y(元),所寄樱桃为x(kg).
(1)求y与x之间的函数关系式;
(2)已知小李给外婆快寄了2.5 kg樱桃,请你求出这次快寄的费用是多少元?
6. “五一节”期间,申老师一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
( http: / / www.21cnjy.com )
(1)求他们出发半小时时,离家多少千米?
(2)求出AB段图象的函数表达式;
(3)他们出发2小时时,离目的地还有多少千米?
7.绵州大剧院举行专场音乐 ( http: / / www.21cnjy.com )会,成人票每张20元,学生票每张5元,暑假期间,为了丰富广大师生的业余文化生活,影剧院制定了两种优惠方案,方案1:购买一张成人票赠送一张学生票;方案2:按总价的90%付款,某校有4名老师与若干名(不少于4人)学生听音乐会.
(1)设学生人数为x(人),付款总金额为y(元),分别建立两种优惠方案中y与x的函数关系式;
(2)请计算并确定出最节省费用的购票方案.
8.为鼓励居民节约用水,某市决定对居民 ( http: / / www.21cnjy.com )用水收费实行“阶梯价”,即当每月用水量不超过15吨时,采用基本价收费;当每月用水量超过15吨时,超过部分每吨采用市场价收费,小兰家四、五月份的用水量及收费情况如下表:
( http: / / www.21cnjy.com )
(1)求该市每吨水的基本价和市场价;
(2)设每月用水量为n吨,应缴水费为m元,请写出m与n之间的函数关系式;
(3)小兰家6月份的用水量为26吨,则她家要交水费多少元?
9.如图1所示,在A、B两地之间有 ( http: / / www.21cnjy.com )汽车站C站,客车由A地驶向C站,货车由B地驶向A地,两车同时出发,匀速行驶,图2是客车、货车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数关系图象.
( http: / / www.21cnjy.com )
(1)填空:A、B两地相距__________千米;
(2)求两小时后,货车离站C的路程y2与行驶时间x之间的函数关系式.
(3)客、货两车何时相遇?
参考答案
1.D 2.A 3.80 4.2
5.(1)当0当x>1时,y=28+10(x-1)=10x+18.
∴y与x的函数关系式为y=
(2)当x=2.5时,y=10×2.5+18=43.
∴小李这次快寄的费用是43元.
6.(1)设OA段图象的函数表达式为y=kx.
∵当x=1.5时,y=90,
∴1.5k=90.∴k=60.
∴y=60x(0≤x≤1.5).
∴当x=0.5时,y=60×0.5=30.
故他们出发半小时时,离家30千米;
(2)设AB段图象的函数表达式为y=k′x+b.
∵A(1.5,90),B(2.5,170)在AB上,
∴解得
∴y=80x-30(1.5≤x≤2.5);
(3)∵当x=2时,y=80×2-30=130,
∴170-130=40(千米).
答:他们出发2小时时,离目的地还有40千米.
7.(1)按优惠方案1可得:y1=20×4+(x-4)×5=5x+60(x≥4),
按优惠方案2可得:y2=(5x+20×4)×90%=4.5x+72(x≥4);
(2)因为y1-y2=0.5x-12(x≥4),
①当y1-y2=0时,得0.5x-12=0,解得x=24.∴当购买24张票时,两种优惠方案付款一样多.
②当y1-y2<0时,得0.5x-12<0,解得x<24.∴4≤x<24时,y1<y2,优惠方案1付款较少.
③当y1-y2>0时,得0.5x-12>0,解得x>24.当x>24时,y1>y2,优惠方案2付款较少.
8.(1)∵当每月用水量不超过15吨时(包括15吨),采用基本价收费;
当每月用水量超过15吨时,超过部分每吨采用市场价收费,且4月份用水22吨,水费51元,5月份用水20吨,水费45元,
∴市场价收费标准为:(51-45)÷(22-20)=3(元/吨),
设基本价收费为x元/吨,根据题意,得
15x+(22-15)×3=51.解得x=2.
故该市每吨水的基本价和市场价分别为:2元/吨,3元/吨.
(2)当n≤15时,m=2n;当n>15时,m=15×2+(n-15)×3=3n-15.
(3)∵小兰家6月份的用水量为26吨,
∴她家要缴水费15×2+(26-15)×3=63(元).
9.(1)440
(2)根据图形可知点D(2,0),
∵两小时前货车的速度为80÷2=40千米/时,
∴货车行驶360千米所需时间为360÷40=9小时.
∴点P(11,360).设直线DP的解析式为y2=kx+b(k≠0),将点D和点P的坐标代入得
解得
所以两小时后,货车离C站的路程y2与时间x之间的函数关系式为y2=40x-80(2≤x≤11).
(3)设直线EF的函数关系式为y1=mx+n(m≠0),将点(6,0)和点(0,360)代入得
解得
故直线EF的函数关系式为y1=-60x+360;
联立直线DP和EF的函数解析式得方程组
解得
答:客、货两车4.4小时相遇.
1.若等腰三角形的周长是80 cm,则能反映这个等腰三角形的腰长y cm与底边长x cm的函数关系式的图象是( )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
2.甲乙两人在直线跑道上同起点、同终点、 ( http: / / www.21cnjy.com )同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒,在跑步的过程中,甲乙两人之间的距离y(m)与乙出发的时间t(s)之间的函数关系如图所示,给出以下结论①a=8,②b=92,③c=123,其中正确的是( )
A.①②③ B.仅有①② C.仅有①③ D.仅有②③
( http: / / www.21cnjy.com )
3.小明放学后步行回家,他离家的路程s(米)与步行时间t(分钟)的函数图象如图所示,则他步行回家的平均速度是__________米/分钟.
( http: / / www.21cnjy.com )
4.李老师开车从甲地到相距240千米的乙地 ( http: / / www.21cnjy.com ),如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图象如图所示,那么到达乙地时油箱剩余油量是__________升.
( http: / / www.21cnjy.com )
5.小李从西安通过某快递公司给在南昌的外婆 ( http: / / www.21cnjy.com )寄一盒樱桃,快递时,他了解到这个公司除了收取每次6元包装费外,樱桃不超过1 kg收费22元,超过1 kg,则超出部分每千克加收10元费用,设该公司从西安到南昌快寄樱桃的费用为y(元),所寄樱桃为x(kg).
(1)求y与x之间的函数关系式;
(2)已知小李给外婆快寄了2.5 kg樱桃,请你求出这次快寄的费用是多少元?
6. “五一节”期间,申老师一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
( http: / / www.21cnjy.com )
(1)求他们出发半小时时,离家多少千米?
(2)求出AB段图象的函数表达式;
(3)他们出发2小时时,离目的地还有多少千米?
7.绵州大剧院举行专场音乐 ( http: / / www.21cnjy.com )会,成人票每张20元,学生票每张5元,暑假期间,为了丰富广大师生的业余文化生活,影剧院制定了两种优惠方案,方案1:购买一张成人票赠送一张学生票;方案2:按总价的90%付款,某校有4名老师与若干名(不少于4人)学生听音乐会.
(1)设学生人数为x(人),付款总金额为y(元),分别建立两种优惠方案中y与x的函数关系式;
(2)请计算并确定出最节省费用的购票方案.
8.为鼓励居民节约用水,某市决定对居民 ( http: / / www.21cnjy.com )用水收费实行“阶梯价”,即当每月用水量不超过15吨时,采用基本价收费;当每月用水量超过15吨时,超过部分每吨采用市场价收费,小兰家四、五月份的用水量及收费情况如下表:
( http: / / www.21cnjy.com )
(1)求该市每吨水的基本价和市场价;
(2)设每月用水量为n吨,应缴水费为m元,请写出m与n之间的函数关系式;
(3)小兰家6月份的用水量为26吨,则她家要交水费多少元?
9.如图1所示,在A、B两地之间有 ( http: / / www.21cnjy.com )汽车站C站,客车由A地驶向C站,货车由B地驶向A地,两车同时出发,匀速行驶,图2是客车、货车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数关系图象.
( http: / / www.21cnjy.com )
(1)填空:A、B两地相距__________千米;
(2)求两小时后,货车离站C的路程y2与行驶时间x之间的函数关系式.
(3)客、货两车何时相遇?
参考答案
1.D 2.A 3.80 4.2
5.(1)当0
∴y与x的函数关系式为y=
(2)当x=2.5时,y=10×2.5+18=43.
∴小李这次快寄的费用是43元.
6.(1)设OA段图象的函数表达式为y=kx.
∵当x=1.5时,y=90,
∴1.5k=90.∴k=60.
∴y=60x(0≤x≤1.5).
∴当x=0.5时,y=60×0.5=30.
故他们出发半小时时,离家30千米;
(2)设AB段图象的函数表达式为y=k′x+b.
∵A(1.5,90),B(2.5,170)在AB上,
∴解得
∴y=80x-30(1.5≤x≤2.5);
(3)∵当x=2时,y=80×2-30=130,
∴170-130=40(千米).
答:他们出发2小时时,离目的地还有40千米.
7.(1)按优惠方案1可得:y1=20×4+(x-4)×5=5x+60(x≥4),
按优惠方案2可得:y2=(5x+20×4)×90%=4.5x+72(x≥4);
(2)因为y1-y2=0.5x-12(x≥4),
①当y1-y2=0时,得0.5x-12=0,解得x=24.∴当购买24张票时,两种优惠方案付款一样多.
②当y1-y2<0时,得0.5x-12<0,解得x<24.∴4≤x<24时,y1<y2,优惠方案1付款较少.
③当y1-y2>0时,得0.5x-12>0,解得x>24.当x>24时,y1>y2,优惠方案2付款较少.
8.(1)∵当每月用水量不超过15吨时(包括15吨),采用基本价收费;
当每月用水量超过15吨时,超过部分每吨采用市场价收费,且4月份用水22吨,水费51元,5月份用水20吨,水费45元,
∴市场价收费标准为:(51-45)÷(22-20)=3(元/吨),
设基本价收费为x元/吨,根据题意,得
15x+(22-15)×3=51.解得x=2.
故该市每吨水的基本价和市场价分别为:2元/吨,3元/吨.
(2)当n≤15时,m=2n;当n>15时,m=15×2+(n-15)×3=3n-15.
(3)∵小兰家6月份的用水量为26吨,
∴她家要缴水费15×2+(26-15)×3=63(元).
9.(1)440
(2)根据图形可知点D(2,0),
∵两小时前货车的速度为80÷2=40千米/时,
∴货车行驶360千米所需时间为360÷40=9小时.
∴点P(11,360).设直线DP的解析式为y2=kx+b(k≠0),将点D和点P的坐标代入得
解得
所以两小时后,货车离C站的路程y2与时间x之间的函数关系式为y2=40x-80(2≤x≤11).
(3)设直线EF的函数关系式为y1=mx+n(m≠0),将点(6,0)和点(0,360)代入得
解得
故直线EF的函数关系式为y1=-60x+360;
联立直线DP和EF的函数解析式得方程组
解得
答:客、货两车4.4小时相遇.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
