人教版2024-2025学年度八年级上册数学第12章全等三角形 单元检测题 (含详解)
文档属性
| 名称 | 人教版2024-2025学年度八年级上册数学第12章全等三角形 单元检测题 (含详解) |  | |
| 格式 | doc | ||
| 文件大小 | 637.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-22 08:07:35 | ||
图片预览

文档简介
人教版2024-2025学年度八年级数学单元检测题
第12章《全等三角形》
时间:100分钟 满分:120分
题号 一 二 三 总分
得分
一.选择题(共10小题,满分30分,每小题3分)
1.如图所示各组中的两个图形属于全等图形的是( )
A. B.
C. D.
2.如图,点A、E、B、D在同一条直线上,且△ABC≌△DEF,下列判断错误的是( )
A.∠C=∠F B.AE=BE C.BC=EF D.EF∥CB
3.下列说法:其中正确的说法为( )
①全等三角形的形状相同、大小相等 ②全等三角形的面积相等
③周长相等的两个三角形全等 ④全等三角形的对应边相等、对应角相等
A.②③④ B.①②③ C.①②④ D.①②③④
4.如图,要测量池塘两岸相对的两点A,B的距离,小明在池塘外取AB的垂线BF上的点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长,依据是( )
A.SSS B.SAS C.ASA D.HL
5.如图,已知AE=AC,∠C=∠E,下列条件中,无法判定△ABC≌△ADE的是( )
A.∠B=∠D B.BC=DE C.∠1=∠2 D.AB=AD
6.用六个如图1的全等△ABC纸片拼接出如图2的正六边形,则图2中∠ACB的度数是( )
A.50° B.45° C.40° D.30°
7.尺规作图中蕴含着丰富的数学知识和思想方法.如图,为了得到∠MBN=∠PAQ,在用直尺和圆规作图的过程中,得到△ACD≌△BEF的依据是( )
A.SAS B.SSS C.ASA D.AAS
8.如图,直线l上有三个正方形a,b,c,若正方形a,c的面积分别为5和11,则正方形b的边长为( )
A.55 B.16 C.6 D.4
9.如图,在△ABC中,BD是△ABC的角平分线,DE⊥AB,若DE=3cm,则点D到BC的距离为( )
A.1.5cm B.2cm C.3cm D.4cm
10.如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°;②∠ADE=∠CDE;③DE=BE;④AD=AB+CD.四个结论中成立的是( )
A.①②④ B.①②③ C.②③④ D.①③
二.填空题(共6小题,满分18分,每小题3分)
11.如图,四边形ABCD≌四边形A′B′C′D′,若∠B=90°,∠C=60°,∠D′=105°,则∠A′= °.
12.如图,△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据“HL”判定,还需要加条件 .
13.如图,△ABC≌△ADE,且AE∥BD,∠ADB=45°,则∠BAC的度数为 .
14.如图,点D在BC上,∠BED=∠CDF=90°,BD=CF,BE=CD.若∠AFD=135°,则∠EDF= .
15.如图,在△ABC中,AD是角平分线,DE⊥AB于E,DF⊥AC于F,DE=2,AC=4,则△ADC的面积为 .
16.如图Rt△ACB中,∠ACB=90°,AD平分∠CAB交BC于D,点E在AB的延长线上,满足∠ADE+∠CAB=180°,若AC=6,BE=2,则线段AB的长为 .
三.解答题(共8小题,满分72分)
17.(6分)如图,点B、E、C、F在同一直线上,∠A=∠D=90°,BE=CF,AC=DF.求证:∠B=∠DEF.
18.(6分)如图,点A,E,F,C在同一条直线上,AF=CE,∠AEB=∠CFD,请你再添加一个条件使得△AEB≌△CFD,并说明理由.
19.(8分)如图所示,海岛上有A、B两个观测点,点B在点A的正东方,海岛C在观测点A的正北方,海岛D在观测点B的正北方,从观测点A看海岛C、D的视角∠CAD与从观测点B看海岛C,D的视角∠CBD相等,那么海岛C、D到观测点A、B所在海岸的距离相等吗?为什么?
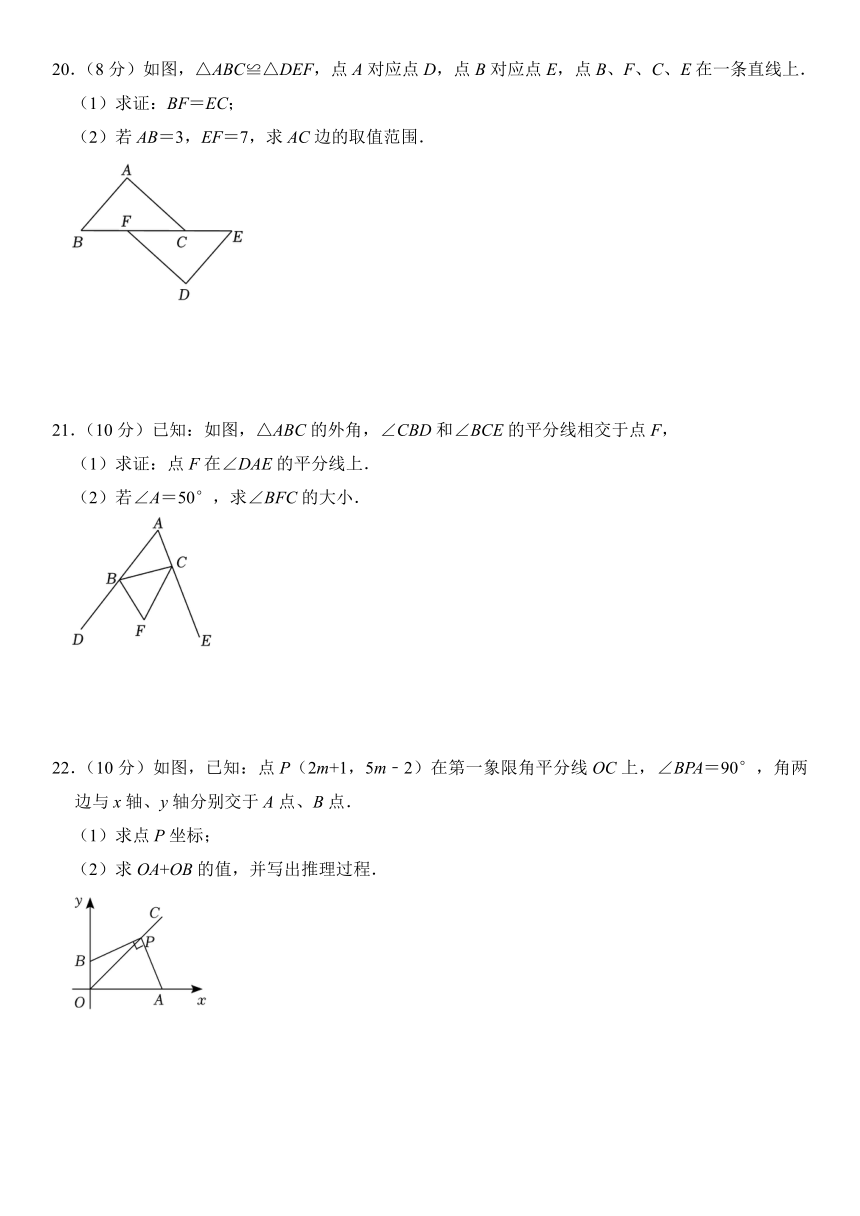
20.(8分)如图,△ABC≌△DEF,点A对应点D,点B对应点E,点B、F、C、E在一条直线上.
(1)求证:BF=EC;
(2)若AB=3,EF=7,求AC边的取值范围.
21.(10分)已知:如图,△ABC的外角,∠CBD和∠BCE的平分线相交于点F,
(1)求证:点F在∠DAE的平分线上.
(2)若∠A=50°,求∠BFC的大小.
22.(10分)如图,已知:点P(2m+1,5m﹣2)在第一象限角平分线OC上,∠BPA=90°,角两边与x轴、y轴分别交于A点、B点.
(1)求点P坐标;
(2)求OA+OB的值,并写出推理过程.
23.(12分)如图(1).AE与BD相交于点C.AC=EC,BC=DC,AB=4cm,点P从点A出发,沿A——B——A的路径以3cm/s的速度运动;方向以tcm/s的速度运动;点Q从点D出发,沿D——E的方向以1cm/s的速度运动,P、Q两点同时出发,当点P到达点A时,P、Q两点同时停止运动,设运动时间为t(s).
(1)求证:AB∥DE;
(2)用含t的式子表示线段AP的长;
(3)连接PQ,当线段PQ经过点C时(如图2).求t的值.
24.(12分)在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF,连接BE,CF.
【发现问题】如图①,若∠BAC=30°,延长BE交CF于点D,则BE与CF的数量关系是 ,∠BDC的度数为 .
【类比探究】如图②,若∠BAC=120°,延长BE,FC相交于点D,请猜想BE与CF的数量关系及∠BDC的度数,并说明理由.
【拓展延伸】如图③,若∠BAC=90°,且点B,E,F在同一条直线上,过点A作AM⊥BF,垂足为点M,请猜想BF,CF,AM之间的数量关系,并说明理由.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:全等图形形状相同,大小相等,
A、两个图形形状不同,故选项不符合题意;
B、两个图形形状相同,大小相等,故选项符合题意;
C、两个图形形状不同,故选项不符合题意;
D、两个图形大小不等,故选项不符合题意.
故选:B.
2.【解答】解:∵△ABC≌△DEF,
∴∠C=∠F,AB=DE,BC=EF,∠ABC=∠DEF,
∴AB﹣BE=DE﹣BE,EF∥CB,
∴AE=DB,
故A,C,D不符合题意,B符合题意.
故选:B.
3.【解答】解:①全等三角形的形状相同、大小相等,正确,故①符合题意;
②全等三角形的面积相等,正确,故②符合题意;
③周长相等的两个三角形不一定全等,故③不符合题意;
④全等三角形的对应边相等、对应角相等,正确,故④符合题意.
∴其中正确的说法为①②④.
故选:C.
4.【解答】解:因为证明在△ABC≌△EDC用到的条件是:CD=BC,∠ABC=∠EDC,∠ACB=∠ECD,
所以用到的是两角及这两角的夹边对应相等即ASA这一方法.
故选:C.
5.【解答】解:A、添加∠B=∠D,由“AAS”可证△ABC≌△ADE,故选项A不合题意;
B、添加BC=DE,由“SAS”可证△ABC≌△ADE,故选项B不合题意;
C、添加∠1=∠2,由“ASA”可证△ABC≌△ADE,故选项C不合题意;
D、添加AB=AD,不能证明△ABC≌△ADE,故选项D符合题意;
故选:D.
6.【解答】解:如下图所示:
∵六边形BCDEFG为正六边形,
∴∠GBC=×(6﹣2)×180°=120°,
∵∠ABC=80°,
∴∠GBH=GBC﹣∠ABC=120°﹣80°=40°,
∵图中的正六边形是有6个全等△ABC纸片拼接的,
∴∠ACB=∠GBH=40°,
故选:C.
7.【解答】解:根据作法可知:AC=BE,AD=BF,CD=EF,
∴△ACD≌△BEF(SSS),
∴∠MBN=∠PAQ,
故选:B.
8.【解答】解:∵三个正方形a,b,c在直线l的同侧,且正方形a、c的边及正方形B的顶点在直线l上,
∴∠CAB=∠BED=180°﹣90°=90°,∠CBD=90°,CB=BD,
∴∠ACB=∠EBD=90°﹣∠ABC,
在△ABC和△EDB中,
,
∴△ABC≌△EDB(AAS),
∴AB=ED,
∵正方形a,c的面积分别为5和11,
∴AC2=5,AB2=DE2=11,
∴BC===4,
∴正方形b的边长为4,
故选:D.
9.【解答】解:如图,过点D作DF⊥BC于F,
∵BD是△ABC的角平分线,DE⊥AB,DF⊥BC,DE=3cm,
∴DF=DE=3cm,
∴点D到BC的距离为3cm,
故选:C.
10.【解答】解:过E作EF⊥AD于F,如图,
∵AB⊥BC,AE平分∠BAD,
∴BE=EF,
在Rt△AEF和Rt△AEB中,
,
∴Rt△AEF≌Rt△AEB(HL),
∴AB=AF,∠AEF=∠AEB,
∵点E是BC的中点,
∴EC=EF=BE,故③错误;
在Rt△EFD和Rt△ECD中,
,
∴Rt△EFD≌Rt△ECD(HL),
∴DC=DF,∠FDE=∠CDE,故②正确;
∴AD=AF+FD=AB+DC,故④正确;
∴∠AED=∠AEF+∠FED=∠BEC=90°,故①正确.
因此正确的有①②④,
故选:A.
二.填空题(共6小题,满分18分,每小题3分)
11.【解答】解:∵四边形ABCD≌四边形A′B′C′D′,
∴∠A=∠A′,∠D=∠D′,
∵∠D′=105°,
∴∠D=105°,
∵∠B=90°,∠C=60°,
∴∠A=105°,
∴∠A′=105°,
故答案为:105.
12.【解答】解:还需添加条件AB=AC,
∵AD⊥BC于D,
∴∠ADB=∠ADC=90°,
在Rt△ABD和Rt△ACD中,
,
∴Rt△ABD≌Rt△ACD(HL),
故答案为:AB=AC.
13.【解答】解:∵AE∥BD,∠ADB=45°,
∴∠EAD=∠ADB=45°,
∵△ABC≌△ADE,
∴∠BAC=∠EAD=45°,
故答案为:45°.
14.【解答】解:∵∠DFC+∠AFD=180°,∠AFD=135°,
∴∠DFC=45°.
又∵∠BED=∠CDF=90°,
在Rt△BDE与Rt△CFD中,
,
∴Rt△BDE≌△Rt△CFD(HL),
∴∠BDE=∠CFD=45°,
∴∠EDF=90°﹣∠BDE=45°.
故答案为:45°.
15.【解答】解:因为AD是角平分线,DE⊥AB于E,DF⊥AC于F,
所以DF=DE=2,
则△ADC的面积=.
故答案为:4.
16.【解答】解:延长AD到M,作DH⊥AB于H.
∵AD平分∠CAB,
∴∠DAC=∠DAH,
∵∠C=∠AHD,AD=AD,
∴△ADC≌△ADH(AAS),
∴AC=AH=6,
∵∠ADE+∠CAB=180°,∠ADE+∠EDM=180°,
∴∠EDM=∠CAB,
∵∠EDM=∠DAE+∠DEA=∠DAE+∠CAD,∠CAD=∠DAB,
∴∠DAB=∠E,
∴DA=DE,
∵DH⊥AE,
∴AH=HE=6,
∵BE=2,
∴BH=4,
∴AB=10,
故答案为:10.
三.解答题(共8小题,满分72分)
17.【解答】证明:∵BE=CF,
∴BE+EC=EC+CF,
即BC=FE.
∵∠A=∠D=90°,
则在Rt△ABC和Rt△DFE中,
,
∴Rt△ABC≌Rt△DFE(HL).
∴∠B=∠DEF.
18.【解答】解:添加{}BE=FD,
理由:∵AF=CE,
∴AE=CF,
在△AEB和△CFD中,
∴△AEB≌△CFD(SAS).
19.【解答】解:相等.
理由:
∵∠CAD=∠CBD,∠COA=∠DOB(对顶角),
∴由内角和定理,得∠C=∠D,
又∵∠CAB=∠DBA=90°,
在△CAB和△DBA中,
∴△CAB≌△DBA(AAS),
∴CA=DB,
∴海岛C、D到观测点A、B所在海岸的距离相等.
20.【解答】(1)证明:∵△ABC≌△DEF,
∴BC=EF,
∴BC﹣CF=EF﹣CF,
∴BF=EC;
(2)解:∵△ABC≌△DEF,EF=7,
∴BC=EF=7,
在△ABC中,BC﹣AB<AC<BC+AB,
∴7﹣3<AC<7+3,
即4<AC<10.
21.【解答】(1)证明:作FM⊥AB于M,FN⊥BC于N,FG⊥AC于G,
∵BF平分∠CBD,FM⊥AB,FN⊥BC,
∴FM=FN,
同理,FG=FN,
∴FM=FG,
又FM⊥AB,FG⊥AC,
∴点F在∠DAE的平分线上;
(2)解:∵BF、CF为△ABC两外角∠CBD、∠BCE的平分线,∠A=50°,
∴∠BCF=(∠A+∠ABC),∠CBF=(∠A+∠ACB);
由三角形内角和定理得:
∠F=180°﹣∠BCF﹣∠CBF=180°﹣[∠A+(∠A+∠ABC+∠ACB)]=180°﹣(∠A+180°)
=90°﹣×50°=90°﹣25°=65°.
22.【解答】解:(1)∵点P(2m+1,5m﹣2)在第一象限角平分线OC上,
∴2m+1=5m﹣2,
解得:m=1,
则点P的坐标为(3,3);
(2)OA+OB=6,推理如下:
过点P分别作x轴、y轴的垂线,垂足分别为D、E,如图,
则∠PDA=∠PEB=90°,
∵∠EOD=90°,
∴∠EPD=∠EPB+∠BPD=90°,
∵∠BPA=∠BPD+∠DPA=90°,
∴∠EPB=∠DPA,
由点P的坐标知,PE=PD=OD=OE=3,
∴△PDA≌△PEB(SAS),
∴DA=BE,
∴OA+OB=OD+DA+OB=OD+BE+OB=OD+OE=3+3=6,
∴OA+OB=6.
23.【解答】(1)证明:在△ABC和△EDC中,
,
∴△ABC≌△EDC(SAS),
∴∠A=∠E,
∴AB∥DE.
(2)解:当0≤t≤时,AP=3t cm;
当<t≤时,BP=(3t﹣4)cm,
则AP=4﹣(3t﹣4)=(8﹣3t)cm;
综上所述,线段AP的长为3t cm或(8﹣3t)cm;
(3)解:由(1)得:∠A=∠E,ED=AB=4cm,
在△ACP和△ECQ中,
,
∴△ACP≌△ECQ(ASA),
∴AP=EQ,
当0≤t≤时,3t=4﹣t,
解得:t=1;
当<t≤时,8﹣3t=4﹣t,
解得:t=2;
综上所述,当线段PQ经过点C时,t的值为1s或2s.
24.【解答】解:(1)BE=CF,∠BDC=30°,
理由如下:如图1所示,设AC与BD交于点O,
∵∠BAC=∠EAF=30°,
∴∠BAC+∠CAE=∠EAF+∠CAE,
即∠BAE=∠CAF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS),
∴BE=CF,∠ABE=∠ACF,
∵∠AOE=∠ABE+∠BAC,∠AOE=∠ACF+∠BDC,
∴∠BDC=∠BAC=30°.
故答案为:BE=CF,30°;
(2)BE=CF,∠BDC=60°,
理由如下:如图2,
∵∠BAC=∠EAF=120°,
∴∠BAC﹣∠EAC=∠EAF﹣∠EAC,
即∠BAE=∠CAF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS),
∴BE=CF,∠AEB=∠AFC,
∵∠EAF=120°,AE=AF,
∴∠AEF=∠AFE=30°,
∴∠BDC=∠BEF﹣∠EFD=∠AEB+30°﹣(∠AFC﹣30°)=60°;
(3)【拓展延伸】BF=CF+2AM,
理由如下:如图3,
∵∠BAC=∠EAF=90°,
∴∠BAC﹣∠EAC=∠EAF﹣∠EAC,
即∠BAE=∠CAF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS),
∴BE=CF,
∵AE=AF,∠EAF=90°,AM⊥EF,
∴AM=EM=FM,即EF=2AM,
∵BF=BE+EF,
∴BF=CF+2AM.
第12章《全等三角形》
时间:100分钟 满分:120分
题号 一 二 三 总分
得分
一.选择题(共10小题,满分30分,每小题3分)
1.如图所示各组中的两个图形属于全等图形的是( )
A. B.
C. D.
2.如图,点A、E、B、D在同一条直线上,且△ABC≌△DEF,下列判断错误的是( )
A.∠C=∠F B.AE=BE C.BC=EF D.EF∥CB
3.下列说法:其中正确的说法为( )
①全等三角形的形状相同、大小相等 ②全等三角形的面积相等
③周长相等的两个三角形全等 ④全等三角形的对应边相等、对应角相等
A.②③④ B.①②③ C.①②④ D.①②③④
4.如图,要测量池塘两岸相对的两点A,B的距离,小明在池塘外取AB的垂线BF上的点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长,依据是( )
A.SSS B.SAS C.ASA D.HL
5.如图,已知AE=AC,∠C=∠E,下列条件中,无法判定△ABC≌△ADE的是( )
A.∠B=∠D B.BC=DE C.∠1=∠2 D.AB=AD
6.用六个如图1的全等△ABC纸片拼接出如图2的正六边形,则图2中∠ACB的度数是( )
A.50° B.45° C.40° D.30°
7.尺规作图中蕴含着丰富的数学知识和思想方法.如图,为了得到∠MBN=∠PAQ,在用直尺和圆规作图的过程中,得到△ACD≌△BEF的依据是( )
A.SAS B.SSS C.ASA D.AAS
8.如图,直线l上有三个正方形a,b,c,若正方形a,c的面积分别为5和11,则正方形b的边长为( )
A.55 B.16 C.6 D.4
9.如图,在△ABC中,BD是△ABC的角平分线,DE⊥AB,若DE=3cm,则点D到BC的距离为( )
A.1.5cm B.2cm C.3cm D.4cm
10.如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°;②∠ADE=∠CDE;③DE=BE;④AD=AB+CD.四个结论中成立的是( )
A.①②④ B.①②③ C.②③④ D.①③
二.填空题(共6小题,满分18分,每小题3分)
11.如图,四边形ABCD≌四边形A′B′C′D′,若∠B=90°,∠C=60°,∠D′=105°,则∠A′= °.
12.如图,△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据“HL”判定,还需要加条件 .
13.如图,△ABC≌△ADE,且AE∥BD,∠ADB=45°,则∠BAC的度数为 .
14.如图,点D在BC上,∠BED=∠CDF=90°,BD=CF,BE=CD.若∠AFD=135°,则∠EDF= .
15.如图,在△ABC中,AD是角平分线,DE⊥AB于E,DF⊥AC于F,DE=2,AC=4,则△ADC的面积为 .
16.如图Rt△ACB中,∠ACB=90°,AD平分∠CAB交BC于D,点E在AB的延长线上,满足∠ADE+∠CAB=180°,若AC=6,BE=2,则线段AB的长为 .
三.解答题(共8小题,满分72分)
17.(6分)如图,点B、E、C、F在同一直线上,∠A=∠D=90°,BE=CF,AC=DF.求证:∠B=∠DEF.
18.(6分)如图,点A,E,F,C在同一条直线上,AF=CE,∠AEB=∠CFD,请你再添加一个条件使得△AEB≌△CFD,并说明理由.
19.(8分)如图所示,海岛上有A、B两个观测点,点B在点A的正东方,海岛C在观测点A的正北方,海岛D在观测点B的正北方,从观测点A看海岛C、D的视角∠CAD与从观测点B看海岛C,D的视角∠CBD相等,那么海岛C、D到观测点A、B所在海岸的距离相等吗?为什么?
20.(8分)如图,△ABC≌△DEF,点A对应点D,点B对应点E,点B、F、C、E在一条直线上.
(1)求证:BF=EC;
(2)若AB=3,EF=7,求AC边的取值范围.
21.(10分)已知:如图,△ABC的外角,∠CBD和∠BCE的平分线相交于点F,
(1)求证:点F在∠DAE的平分线上.
(2)若∠A=50°,求∠BFC的大小.
22.(10分)如图,已知:点P(2m+1,5m﹣2)在第一象限角平分线OC上,∠BPA=90°,角两边与x轴、y轴分别交于A点、B点.
(1)求点P坐标;
(2)求OA+OB的值,并写出推理过程.
23.(12分)如图(1).AE与BD相交于点C.AC=EC,BC=DC,AB=4cm,点P从点A出发,沿A——B——A的路径以3cm/s的速度运动;方向以tcm/s的速度运动;点Q从点D出发,沿D——E的方向以1cm/s的速度运动,P、Q两点同时出发,当点P到达点A时,P、Q两点同时停止运动,设运动时间为t(s).
(1)求证:AB∥DE;
(2)用含t的式子表示线段AP的长;
(3)连接PQ,当线段PQ经过点C时(如图2).求t的值.
24.(12分)在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF,连接BE,CF.
【发现问题】如图①,若∠BAC=30°,延长BE交CF于点D,则BE与CF的数量关系是 ,∠BDC的度数为 .
【类比探究】如图②,若∠BAC=120°,延长BE,FC相交于点D,请猜想BE与CF的数量关系及∠BDC的度数,并说明理由.
【拓展延伸】如图③,若∠BAC=90°,且点B,E,F在同一条直线上,过点A作AM⊥BF,垂足为点M,请猜想BF,CF,AM之间的数量关系,并说明理由.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:全等图形形状相同,大小相等,
A、两个图形形状不同,故选项不符合题意;
B、两个图形形状相同,大小相等,故选项符合题意;
C、两个图形形状不同,故选项不符合题意;
D、两个图形大小不等,故选项不符合题意.
故选:B.
2.【解答】解:∵△ABC≌△DEF,
∴∠C=∠F,AB=DE,BC=EF,∠ABC=∠DEF,
∴AB﹣BE=DE﹣BE,EF∥CB,
∴AE=DB,
故A,C,D不符合题意,B符合题意.
故选:B.
3.【解答】解:①全等三角形的形状相同、大小相等,正确,故①符合题意;
②全等三角形的面积相等,正确,故②符合题意;
③周长相等的两个三角形不一定全等,故③不符合题意;
④全等三角形的对应边相等、对应角相等,正确,故④符合题意.
∴其中正确的说法为①②④.
故选:C.
4.【解答】解:因为证明在△ABC≌△EDC用到的条件是:CD=BC,∠ABC=∠EDC,∠ACB=∠ECD,
所以用到的是两角及这两角的夹边对应相等即ASA这一方法.
故选:C.
5.【解答】解:A、添加∠B=∠D,由“AAS”可证△ABC≌△ADE,故选项A不合题意;
B、添加BC=DE,由“SAS”可证△ABC≌△ADE,故选项B不合题意;
C、添加∠1=∠2,由“ASA”可证△ABC≌△ADE,故选项C不合题意;
D、添加AB=AD,不能证明△ABC≌△ADE,故选项D符合题意;
故选:D.
6.【解答】解:如下图所示:
∵六边形BCDEFG为正六边形,
∴∠GBC=×(6﹣2)×180°=120°,
∵∠ABC=80°,
∴∠GBH=GBC﹣∠ABC=120°﹣80°=40°,
∵图中的正六边形是有6个全等△ABC纸片拼接的,
∴∠ACB=∠GBH=40°,
故选:C.
7.【解答】解:根据作法可知:AC=BE,AD=BF,CD=EF,
∴△ACD≌△BEF(SSS),
∴∠MBN=∠PAQ,
故选:B.
8.【解答】解:∵三个正方形a,b,c在直线l的同侧,且正方形a、c的边及正方形B的顶点在直线l上,
∴∠CAB=∠BED=180°﹣90°=90°,∠CBD=90°,CB=BD,
∴∠ACB=∠EBD=90°﹣∠ABC,
在△ABC和△EDB中,
,
∴△ABC≌△EDB(AAS),
∴AB=ED,
∵正方形a,c的面积分别为5和11,
∴AC2=5,AB2=DE2=11,
∴BC===4,
∴正方形b的边长为4,
故选:D.
9.【解答】解:如图,过点D作DF⊥BC于F,
∵BD是△ABC的角平分线,DE⊥AB,DF⊥BC,DE=3cm,
∴DF=DE=3cm,
∴点D到BC的距离为3cm,
故选:C.
10.【解答】解:过E作EF⊥AD于F,如图,
∵AB⊥BC,AE平分∠BAD,
∴BE=EF,
在Rt△AEF和Rt△AEB中,
,
∴Rt△AEF≌Rt△AEB(HL),
∴AB=AF,∠AEF=∠AEB,
∵点E是BC的中点,
∴EC=EF=BE,故③错误;
在Rt△EFD和Rt△ECD中,
,
∴Rt△EFD≌Rt△ECD(HL),
∴DC=DF,∠FDE=∠CDE,故②正确;
∴AD=AF+FD=AB+DC,故④正确;
∴∠AED=∠AEF+∠FED=∠BEC=90°,故①正确.
因此正确的有①②④,
故选:A.
二.填空题(共6小题,满分18分,每小题3分)
11.【解答】解:∵四边形ABCD≌四边形A′B′C′D′,
∴∠A=∠A′,∠D=∠D′,
∵∠D′=105°,
∴∠D=105°,
∵∠B=90°,∠C=60°,
∴∠A=105°,
∴∠A′=105°,
故答案为:105.
12.【解答】解:还需添加条件AB=AC,
∵AD⊥BC于D,
∴∠ADB=∠ADC=90°,
在Rt△ABD和Rt△ACD中,
,
∴Rt△ABD≌Rt△ACD(HL),
故答案为:AB=AC.
13.【解答】解:∵AE∥BD,∠ADB=45°,
∴∠EAD=∠ADB=45°,
∵△ABC≌△ADE,
∴∠BAC=∠EAD=45°,
故答案为:45°.
14.【解答】解:∵∠DFC+∠AFD=180°,∠AFD=135°,
∴∠DFC=45°.
又∵∠BED=∠CDF=90°,
在Rt△BDE与Rt△CFD中,
,
∴Rt△BDE≌△Rt△CFD(HL),
∴∠BDE=∠CFD=45°,
∴∠EDF=90°﹣∠BDE=45°.
故答案为:45°.
15.【解答】解:因为AD是角平分线,DE⊥AB于E,DF⊥AC于F,
所以DF=DE=2,
则△ADC的面积=.
故答案为:4.
16.【解答】解:延长AD到M,作DH⊥AB于H.
∵AD平分∠CAB,
∴∠DAC=∠DAH,
∵∠C=∠AHD,AD=AD,
∴△ADC≌△ADH(AAS),
∴AC=AH=6,
∵∠ADE+∠CAB=180°,∠ADE+∠EDM=180°,
∴∠EDM=∠CAB,
∵∠EDM=∠DAE+∠DEA=∠DAE+∠CAD,∠CAD=∠DAB,
∴∠DAB=∠E,
∴DA=DE,
∵DH⊥AE,
∴AH=HE=6,
∵BE=2,
∴BH=4,
∴AB=10,
故答案为:10.
三.解答题(共8小题,满分72分)
17.【解答】证明:∵BE=CF,
∴BE+EC=EC+CF,
即BC=FE.
∵∠A=∠D=90°,
则在Rt△ABC和Rt△DFE中,
,
∴Rt△ABC≌Rt△DFE(HL).
∴∠B=∠DEF.
18.【解答】解:添加{}BE=FD,
理由:∵AF=CE,
∴AE=CF,
在△AEB和△CFD中,
∴△AEB≌△CFD(SAS).
19.【解答】解:相等.
理由:
∵∠CAD=∠CBD,∠COA=∠DOB(对顶角),
∴由内角和定理,得∠C=∠D,
又∵∠CAB=∠DBA=90°,
在△CAB和△DBA中,
∴△CAB≌△DBA(AAS),
∴CA=DB,
∴海岛C、D到观测点A、B所在海岸的距离相等.
20.【解答】(1)证明:∵△ABC≌△DEF,
∴BC=EF,
∴BC﹣CF=EF﹣CF,
∴BF=EC;
(2)解:∵△ABC≌△DEF,EF=7,
∴BC=EF=7,
在△ABC中,BC﹣AB<AC<BC+AB,
∴7﹣3<AC<7+3,
即4<AC<10.
21.【解答】(1)证明:作FM⊥AB于M,FN⊥BC于N,FG⊥AC于G,
∵BF平分∠CBD,FM⊥AB,FN⊥BC,
∴FM=FN,
同理,FG=FN,
∴FM=FG,
又FM⊥AB,FG⊥AC,
∴点F在∠DAE的平分线上;
(2)解:∵BF、CF为△ABC两外角∠CBD、∠BCE的平分线,∠A=50°,
∴∠BCF=(∠A+∠ABC),∠CBF=(∠A+∠ACB);
由三角形内角和定理得:
∠F=180°﹣∠BCF﹣∠CBF=180°﹣[∠A+(∠A+∠ABC+∠ACB)]=180°﹣(∠A+180°)
=90°﹣×50°=90°﹣25°=65°.
22.【解答】解:(1)∵点P(2m+1,5m﹣2)在第一象限角平分线OC上,
∴2m+1=5m﹣2,
解得:m=1,
则点P的坐标为(3,3);
(2)OA+OB=6,推理如下:
过点P分别作x轴、y轴的垂线,垂足分别为D、E,如图,
则∠PDA=∠PEB=90°,
∵∠EOD=90°,
∴∠EPD=∠EPB+∠BPD=90°,
∵∠BPA=∠BPD+∠DPA=90°,
∴∠EPB=∠DPA,
由点P的坐标知,PE=PD=OD=OE=3,
∴△PDA≌△PEB(SAS),
∴DA=BE,
∴OA+OB=OD+DA+OB=OD+BE+OB=OD+OE=3+3=6,
∴OA+OB=6.
23.【解答】(1)证明:在△ABC和△EDC中,
,
∴△ABC≌△EDC(SAS),
∴∠A=∠E,
∴AB∥DE.
(2)解:当0≤t≤时,AP=3t cm;
当<t≤时,BP=(3t﹣4)cm,
则AP=4﹣(3t﹣4)=(8﹣3t)cm;
综上所述,线段AP的长为3t cm或(8﹣3t)cm;
(3)解:由(1)得:∠A=∠E,ED=AB=4cm,
在△ACP和△ECQ中,
,
∴△ACP≌△ECQ(ASA),
∴AP=EQ,
当0≤t≤时,3t=4﹣t,
解得:t=1;
当<t≤时,8﹣3t=4﹣t,
解得:t=2;
综上所述,当线段PQ经过点C时,t的值为1s或2s.
24.【解答】解:(1)BE=CF,∠BDC=30°,
理由如下:如图1所示,设AC与BD交于点O,
∵∠BAC=∠EAF=30°,
∴∠BAC+∠CAE=∠EAF+∠CAE,
即∠BAE=∠CAF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS),
∴BE=CF,∠ABE=∠ACF,
∵∠AOE=∠ABE+∠BAC,∠AOE=∠ACF+∠BDC,
∴∠BDC=∠BAC=30°.
故答案为:BE=CF,30°;
(2)BE=CF,∠BDC=60°,
理由如下:如图2,
∵∠BAC=∠EAF=120°,
∴∠BAC﹣∠EAC=∠EAF﹣∠EAC,
即∠BAE=∠CAF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS),
∴BE=CF,∠AEB=∠AFC,
∵∠EAF=120°,AE=AF,
∴∠AEF=∠AFE=30°,
∴∠BDC=∠BEF﹣∠EFD=∠AEB+30°﹣(∠AFC﹣30°)=60°;
(3)【拓展延伸】BF=CF+2AM,
理由如下:如图3,
∵∠BAC=∠EAF=90°,
∴∠BAC﹣∠EAC=∠EAF﹣∠EAC,
即∠BAE=∠CAF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS),
∴BE=CF,
∵AE=AF,∠EAF=90°,AM⊥EF,
∴AM=EM=FM,即EF=2AM,
∵BF=BE+EF,
∴BF=CF+2AM.
