11.3.2多边形的内角和 课件(共25张PPT)
文档属性
| 名称 | 11.3.2多边形的内角和 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-23 11:33:27 | ||
图片预览



文档简介
(共25张PPT)
人教版 八年级数学上
11.3.2 多边形的内角和
学习目标
1.掌握多边形的内角和与外角和公式.(重点)
2.学会运用多边形的内角和与外角和公式解决有关问题.(难点)
温故知新
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
1.说一说什么是多边形?
3.从n边形的一个顶点出发,可以引出_______条对角线,将多边形
分割成了________个三角形.
2.说一说什么是多边形的对角线?
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
n-3
n-2
合作探究---多边形内角和
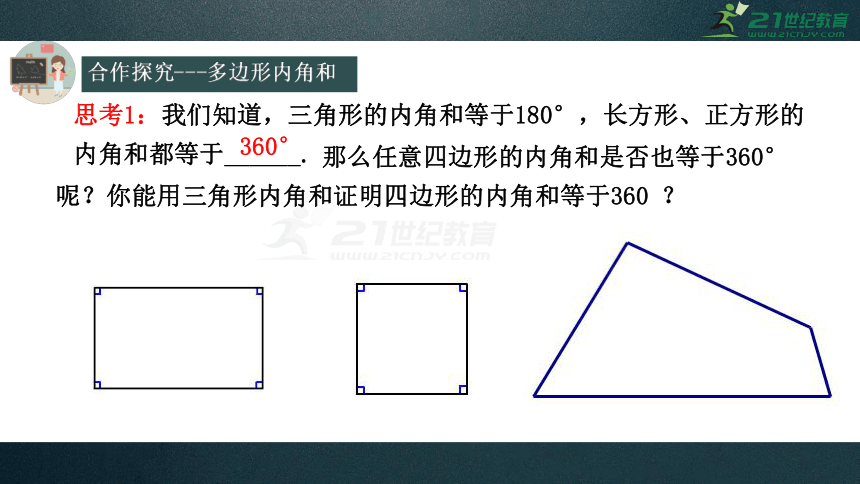
思考1:我们知道,三角形的内角和等于180°,长方形、正方形的内角和都等于______.
那么任意四边形的内角和是否也等于360°呢?你能用三角形内角和证明四边形的内角和等于360 ?
360°
合作探究---多边形内角和
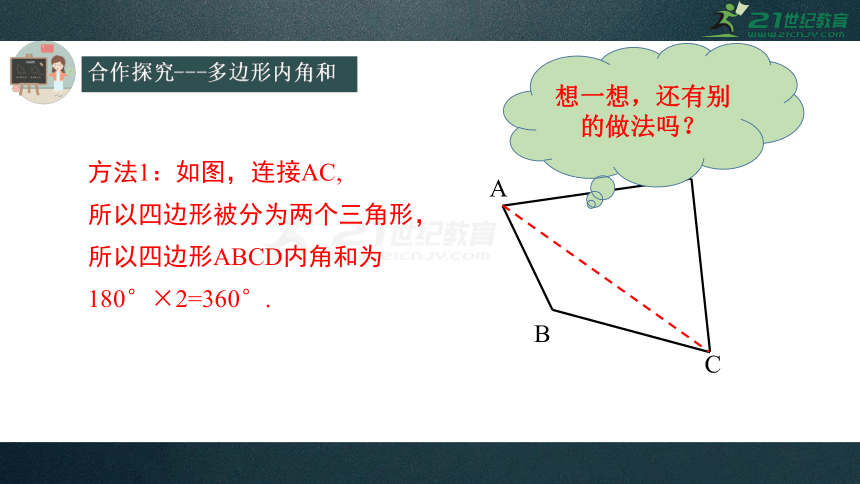
方法1:如图,连接AC,
所以四边形被分为两个三角形,
所以四边形ABCD内角和为
180°×2=360°.
A
B
C
D
想一想,还有别的做法吗?
合作探究---多边形内角和
A
B
C
D
E
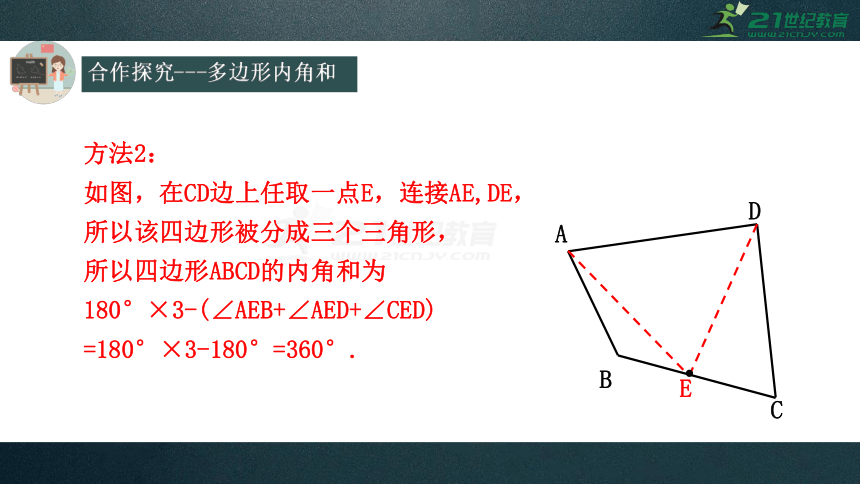
方法2:
如图,在CD边上任取一点E,连接AE,DE,
所以该四边形被分成三个三角形,
所以四边形ABCD的内角和为
180°×3-(∠AEB+∠AED+∠CED)
=180°×3-180°=360°.
合作探究---多边形内角和
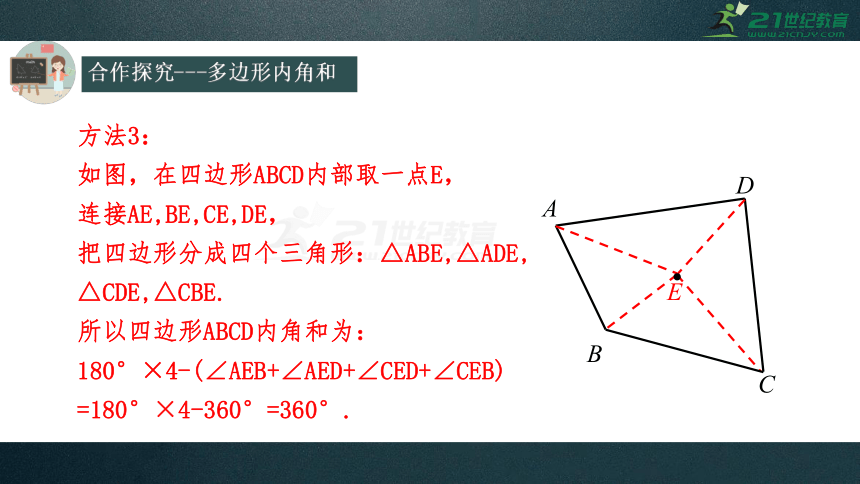
方法3:
如图,在四边形ABCD内部取一点E,
连接AE,BE,CE,DE,
把四边形分成四个三角形:△ABE,△ADE,
△CDE,△CBE.
所以四边形ABCD内角和为:
180°×4-(∠AEB+∠AED+∠CED+∠CEB)
=180°×4-360°=360°.
A
B
C
D
E
合作探究---多边形内角和
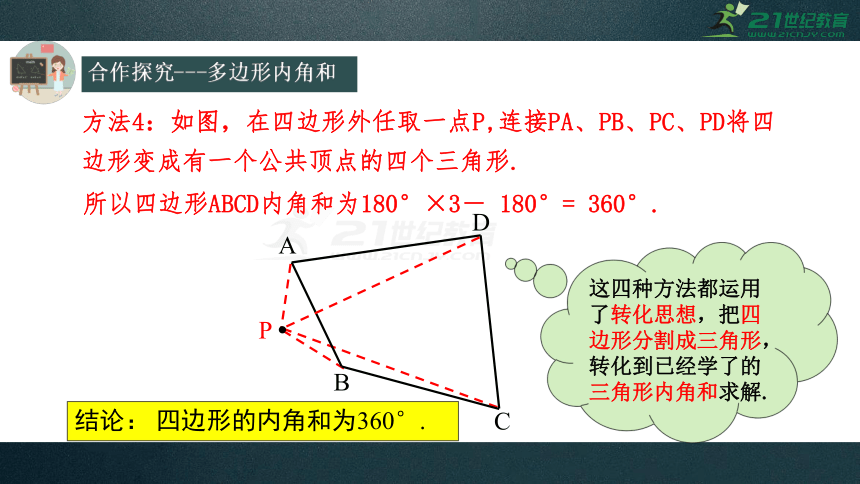
A
B
C
D
P
方法4:如图,在四边形外任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形.
所以四边形ABCD内角和为180°×3- 180°= 360°.
这四种方法都运用了转化思想,把四边形分割成三角形,转化到已经学了的三角形内角和求解.
结论: 四边形的内角和为360°.
合作探究---多边形内角和
A
C
D
E
B
A
B
C
D
E
F
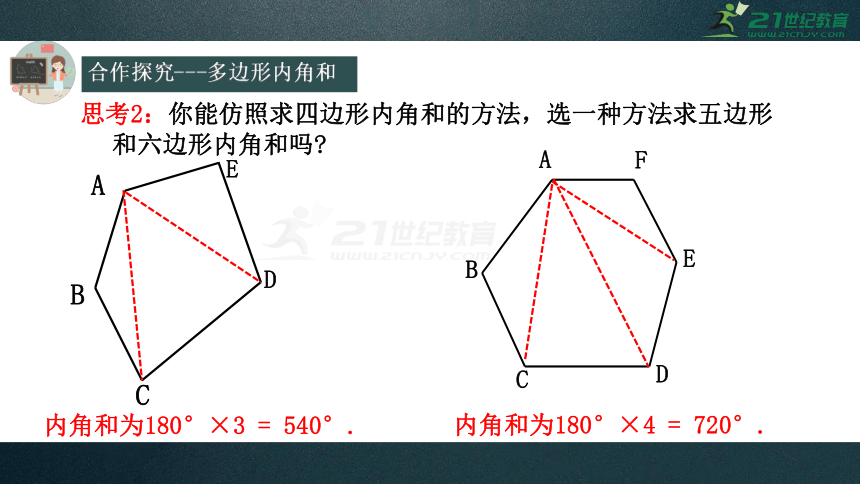
思考2:你能仿照求四边形内角和的方法,选一种方法求五边形和六边形内角和吗
内角和为180°×3 = 540°.
内角和为180°×4 = 720°.
合作探究---多边形内角和
2
3
180°×3
=540°
3
4
180°×4
=720°
n-3
n-2
180°×(n - 2)
由特殊到一般:n 边形的内角和等于(n -2)×180°
小试牛刀
1.六边形的内角和等于( )
A.360° B.720°
C.1080° D.1260°
B
2.内角和是540°的多边形是( )
D
A
B
C
D
典例精析
例1、如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
解:
如图,四边形ABCD中,∠A+ ∠C =180°.
∠A+∠B+∠C+∠D=(4-2) ×180 °= 360 °,
因为
∠B+∠D= 360°-(∠A+∠C)
= 360°- 180° =180°.
所以
A
B
C
D
如果一个四边形的一组对角互补,那么另一组对角互补.
变式训练
如图,在四边形ABCD中, ∠A与∠C互补, BE平分∠ABC,DF平分∠ADC,若BE∥DF,求证:△DCF为直角三角形.
证明:∵在四边形ABCD中,∠A与∠C互补,
∴∠ABC+∠ADC=180°,
∵BE平分∠ABC,DF平分∠ADC,
∴∠CDF+∠EBF=90°,
∵BE∥DF,∴∠EBF=∠CFD,
∴∠CDF+∠CFD=90°,
故△DCF为直角三角形.
合作探究---多边形外角和
思考3:在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.你能求出六边形的外角和吗?
解:∵六边形的任何一个外角加上与它相邻的内角
都等于180 °,
∴六边形的6个外角加上与它们相邻的内角,所得总和等于6×180°.
∴六边形外角和=总和-内角和
=6×180°-(6-2)×180°=2×180°=360°
合作探究---多边形外角和
由特殊到一般:在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
n边形的外角和等于360°.
-(n-2) × 180°
=360 °
=n个平角-n边形内角和
= n×180 °
An
A2
A3
A4
1
2
3
4
n
A1
思考4:n边形的外角和又是多少呢?
与边数无关
思考5:回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
即时小练:
(1)若一个正多边形的内角是150°,那么这是正 ____边形.
(2)已知多边形的每个外角都是40°,则这个多边形是 ______边形.
十二
九
合作探究---多边形外角和
实战演练
1.若正n边形每一个内角等于它相邻外角的2倍,则n的值是( ).
A.4 B.5 C.6 D.7
2.已知一个多边形,它的内角和等于外角和的3倍,求这个多边形的
边数 .
C
8
3.若一个正n多边形的每个内角为144°,则这个正n多边形的所有对角线的条数是 .
35
实战演练
3.一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?
解:设这个多边形边数为n,则(n-2) 180=360+720,
解得n=8,
∵这个多边形的每个内角都相等,
且内角和为(8-2)×180°=1080°,
∴它每一个内角的度数为1080°÷8=135°.
实战演练
4.已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
解:∵360°÷180°=2,
630°÷180°=3......90°,
∴甲的说法对,乙的说法不对,
360°÷180°+2=4.
故甲同学说的边数n是4;
实战演练
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
解:依题意有
(n+x-2)×180°-(n-2)×180°=360°,
解得x=2.
故x的值是2.
拓展创新
1.如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
解:如图,
∵∠3+∠4=∠8+∠9,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠8+∠9+∠5+∠6+∠7=五边形的内角和=540°.
8
9
拓展创新
2.某厂生产一块模板的示意图如图,已知该模板的边AB∥CF,
CD∥AE,按规定AB、CD的延长线相交成80°角,因交点不在模
板上不便测量,这时师傅告诉徒弟只需测量一个角,便知道AB、
CD的延长线的夹角是否符合规定,需测哪一个角?说明理由。
解:只需测∠C。理由如下:
分别延长AB、CD,两线相较于点M,
因为AB∥CF,即AM∥CF,
所以∠C+∠M=180°所以测出∠C即可。
A
D
C
F
E
B
M
课后作业
今天我们收获了哪些知识?(畅所欲言)
1.说一说多边形内角和公式?
2.在探究多边形内角和公式中,连接对角线起到什么作用?
3.多边形的外角和等于多少?
4.正多边形的一个外角和一个内角的公式是什么?
课后作业
教材25页习题11.3第5、6、7、8题.
https://www.21cnjy.com/help/help_extract.php
人教版 八年级数学上
11.3.2 多边形的内角和
学习目标
1.掌握多边形的内角和与外角和公式.(重点)
2.学会运用多边形的内角和与外角和公式解决有关问题.(难点)
温故知新
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
1.说一说什么是多边形?
3.从n边形的一个顶点出发,可以引出_______条对角线,将多边形
分割成了________个三角形.
2.说一说什么是多边形的对角线?
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
n-3
n-2
合作探究---多边形内角和
思考1:我们知道,三角形的内角和等于180°,长方形、正方形的内角和都等于______.
那么任意四边形的内角和是否也等于360°呢?你能用三角形内角和证明四边形的内角和等于360 ?
360°
合作探究---多边形内角和
方法1:如图,连接AC,
所以四边形被分为两个三角形,
所以四边形ABCD内角和为
180°×2=360°.
A
B
C
D
想一想,还有别的做法吗?
合作探究---多边形内角和
A
B
C
D
E
方法2:
如图,在CD边上任取一点E,连接AE,DE,
所以该四边形被分成三个三角形,
所以四边形ABCD的内角和为
180°×3-(∠AEB+∠AED+∠CED)
=180°×3-180°=360°.
合作探究---多边形内角和
方法3:
如图,在四边形ABCD内部取一点E,
连接AE,BE,CE,DE,
把四边形分成四个三角形:△ABE,△ADE,
△CDE,△CBE.
所以四边形ABCD内角和为:
180°×4-(∠AEB+∠AED+∠CED+∠CEB)
=180°×4-360°=360°.
A
B
C
D
E
合作探究---多边形内角和
A
B
C
D
P
方法4:如图,在四边形外任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形.
所以四边形ABCD内角和为180°×3- 180°= 360°.
这四种方法都运用了转化思想,把四边形分割成三角形,转化到已经学了的三角形内角和求解.
结论: 四边形的内角和为360°.
合作探究---多边形内角和
A
C
D
E
B
A
B
C
D
E
F
思考2:你能仿照求四边形内角和的方法,选一种方法求五边形和六边形内角和吗
内角和为180°×3 = 540°.
内角和为180°×4 = 720°.
合作探究---多边形内角和
2
3
180°×3
=540°
3
4
180°×4
=720°
n-3
n-2
180°×(n - 2)
由特殊到一般:n 边形的内角和等于(n -2)×180°
小试牛刀
1.六边形的内角和等于( )
A.360° B.720°
C.1080° D.1260°
B
2.内角和是540°的多边形是( )
D
A
B
C
D
典例精析
例1、如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
解:
如图,四边形ABCD中,∠A+ ∠C =180°.
∠A+∠B+∠C+∠D=(4-2) ×180 °= 360 °,
因为
∠B+∠D= 360°-(∠A+∠C)
= 360°- 180° =180°.
所以
A
B
C
D
如果一个四边形的一组对角互补,那么另一组对角互补.
变式训练
如图,在四边形ABCD中, ∠A与∠C互补, BE平分∠ABC,DF平分∠ADC,若BE∥DF,求证:△DCF为直角三角形.
证明:∵在四边形ABCD中,∠A与∠C互补,
∴∠ABC+∠ADC=180°,
∵BE平分∠ABC,DF平分∠ADC,
∴∠CDF+∠EBF=90°,
∵BE∥DF,∴∠EBF=∠CFD,
∴∠CDF+∠CFD=90°,
故△DCF为直角三角形.
合作探究---多边形外角和
思考3:在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.你能求出六边形的外角和吗?
解:∵六边形的任何一个外角加上与它相邻的内角
都等于180 °,
∴六边形的6个外角加上与它们相邻的内角,所得总和等于6×180°.
∴六边形外角和=总和-内角和
=6×180°-(6-2)×180°=2×180°=360°
合作探究---多边形外角和
由特殊到一般:在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
n边形的外角和等于360°.
-(n-2) × 180°
=360 °
=n个平角-n边形内角和
= n×180 °
An
A2
A3
A4
1
2
3
4
n
A1
思考4:n边形的外角和又是多少呢?
与边数无关
思考5:回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
即时小练:
(1)若一个正多边形的内角是150°,那么这是正 ____边形.
(2)已知多边形的每个外角都是40°,则这个多边形是 ______边形.
十二
九
合作探究---多边形外角和
实战演练
1.若正n边形每一个内角等于它相邻外角的2倍,则n的值是( ).
A.4 B.5 C.6 D.7
2.已知一个多边形,它的内角和等于外角和的3倍,求这个多边形的
边数 .
C
8
3.若一个正n多边形的每个内角为144°,则这个正n多边形的所有对角线的条数是 .
35
实战演练
3.一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?
解:设这个多边形边数为n,则(n-2) 180=360+720,
解得n=8,
∵这个多边形的每个内角都相等,
且内角和为(8-2)×180°=1080°,
∴它每一个内角的度数为1080°÷8=135°.
实战演练
4.已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
解:∵360°÷180°=2,
630°÷180°=3......90°,
∴甲的说法对,乙的说法不对,
360°÷180°+2=4.
故甲同学说的边数n是4;
实战演练
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
解:依题意有
(n+x-2)×180°-(n-2)×180°=360°,
解得x=2.
故x的值是2.
拓展创新
1.如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
解:如图,
∵∠3+∠4=∠8+∠9,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠8+∠9+∠5+∠6+∠7=五边形的内角和=540°.
8
9
拓展创新
2.某厂生产一块模板的示意图如图,已知该模板的边AB∥CF,
CD∥AE,按规定AB、CD的延长线相交成80°角,因交点不在模
板上不便测量,这时师傅告诉徒弟只需测量一个角,便知道AB、
CD的延长线的夹角是否符合规定,需测哪一个角?说明理由。
解:只需测∠C。理由如下:
分别延长AB、CD,两线相较于点M,
因为AB∥CF,即AM∥CF,
所以∠C+∠M=180°所以测出∠C即可。
A
D
C
F
E
B
M
课后作业
今天我们收获了哪些知识?(畅所欲言)
1.说一说多边形内角和公式?
2.在探究多边形内角和公式中,连接对角线起到什么作用?
3.多边形的外角和等于多少?
4.正多边形的一个外角和一个内角的公式是什么?
课后作业
教材25页习题11.3第5、6、7、8题.
https://www.21cnjy.com/help/help_extract.php
