7.5正态分布 课件(共26张PPT) -高中数学人教版(2019)选择性必修第三册
文档属性
| 名称 | 7.5正态分布 课件(共26张PPT) -高中数学人教版(2019)选择性必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-22 20:06:42 | ||
图片预览





文档简介
(共26张PPT)
第七章 随机变量及其分布
7.5 正态分布
高中数学人教A版(2019)选择性必修第三
复习回顾
回顾前面已经研究过哪些重要的离散型随机变量
二项分布:
一般地,在n重伯努利试验中,设每次试验中事件A发生的概率为p (0P(X=k)=Ch×pk×(1-p)"-k,(k=0,1,2,..,n).
如果随机变量X的分布列具有上式的形式,则称随机变量X服从二项分布 ,记作X~B(n,p).
二项分布的均值与方差:
若X~B(n,p), 则有
E(X)= np ,D(X)= np(1-p) .
复习回顾
回顾前面已经研究过哪些重要的离散型随机变量
超几何分布及其分布列
一般地,假设一批产品共有N件,其中有M件次品.从N件产品中随机 抽取n件(不放回),用X 表示抽取的n件产品中的次品数,则X 的分布列为
,k=m,m+1,m+2,..,r.
超几何分布的均值与方差
E(X)=mp(其中 、
新课导入
现实中,还有大量问题中的随机变量不是离散的,例如
在生产中,在正常生产条件下各种产品的质量指标(如零件的尺寸、维的 纤度等);
在测量中,长度测量误差,某一地区同年龄人群的身高、体重等;
在生物学中,一定条件下生长的小麦的株高、穗长、单位面积产量等; 在气象中,某地每年七月份的平均气温、平均湿度以及降雨量等;
它们的取值往往充满某个区间甚至整个实轴,但取一点的概率为0,我
们称这类随机变量为连续性随机变量,这就是我们所要学习的正态分布。
☆ 新知探究
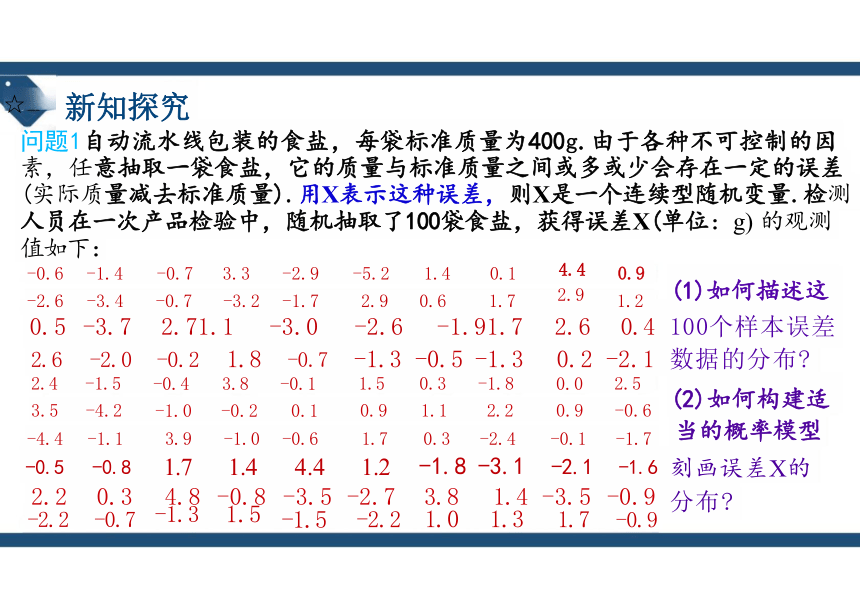
问题1自动流水线包装的食盐,每袋标准质量为400g.由于各种不可控制的因 素,任意抽取一袋食盐,它的质量与标准质量之间或多或少会存在一定的误差 (实际质量减去标准质量).用X表示这种误差,则X是一个连续型随机变量.检测 人员在一次产品检验中,随机抽取了100袋食盐,获得误差X(单位:g) 的观测 值如下:
(1)如何描述这
100个样本误差
数据的分布
(2)如何构建适 当的概率模型
刻画误差X的
分布
1.4 0.1
0.6 1.7
-1.91.7
-0.5 -1.3
0.3 -1.8
1.1 2.2
0.3 -2.4
-1.8 -3.1
3.8 1.4
1.0 1.3
-0.6 -1.4
-2.6 -3.4
0.5 -3.7
2.6 -2.0
2.4 -1.5
3.5 -4.2
-4.4 -1.1
-0.5 -0.8
2.2 0.3
-2.2 -0.7
-0.2 -0.4 -1.0 3.9 1.7 4.8 -1.3
1.8
3.8
-0.2
-1.0
1.4
-0.8
1.5
-2.9
-1.7
-3.0
-0.7
-0.1
0.1
-0.6
4.4
-3.5
-1.5
-5.2
2.9
-2.6
-1.3
1.5
0.9
1.7
1.2
-2.7
-2.2
0.9
1.2
0.4
-2.1
2.5
-0.6
-1.7
-1.6
-0.9
-0.9
4.4
2.9
2.6
0.2
0.0
0.9
-0.1
-2.1
-3.5
1.7
-0.7 3.3
-0.7 -3.2
2.71.1
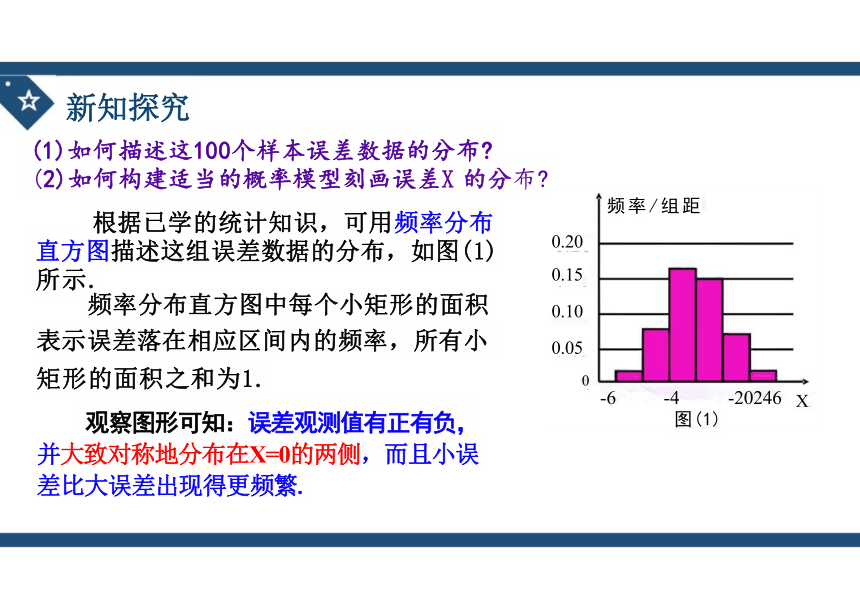
根据已学的统计知识,可用频率分布 直方图描述这组误差数据的分布,如图(1) 所示.
频率分布直方图中每个小矩形的面积
表示误差落在相应区间内的频率,所有小 矩形的面积之和为1.
观察图形可知:误差观测值有正有负, 并大致对称地分布在X=0的两侧,而且小误 差比大误差出现得更频繁.
新知探究
(1)如何描述这100个样本误差数据的分布
(2)如何构建适当的概率模型刻画误差X 的分布
频率/组距
-6 -4 -20246 X
图(1)
0.20
0.15 0.10 0.05 0
新知探究
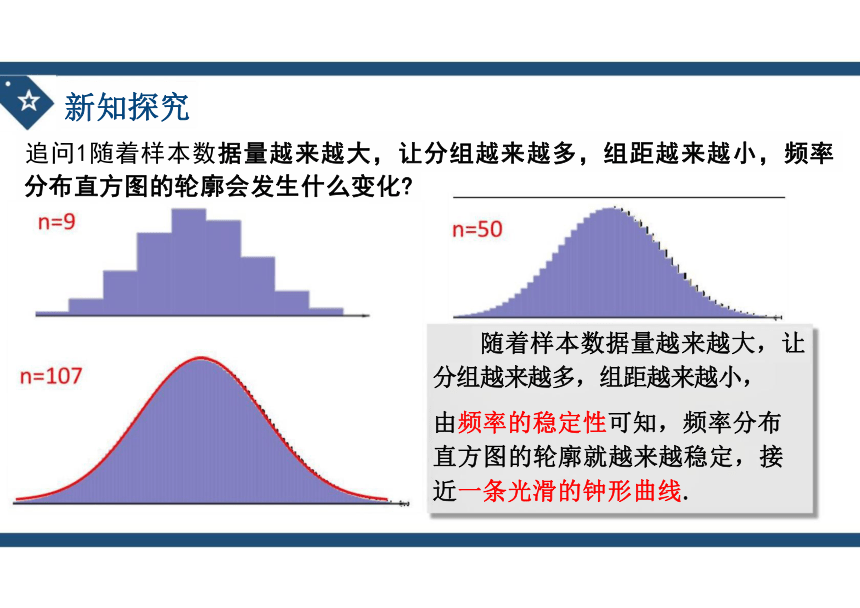
追问1随着样本数据量越来越大,让分组越来越多,组距越来越小,频率
随着样本数据量越来越大,让
分组越来越多,组距越来越小,
由频率的稳定性可知,频率分布 直方图的轮廓就越来越稳定,接 近一条光滑的钟形曲线.
分布直方图的轮廓会发生什么变化
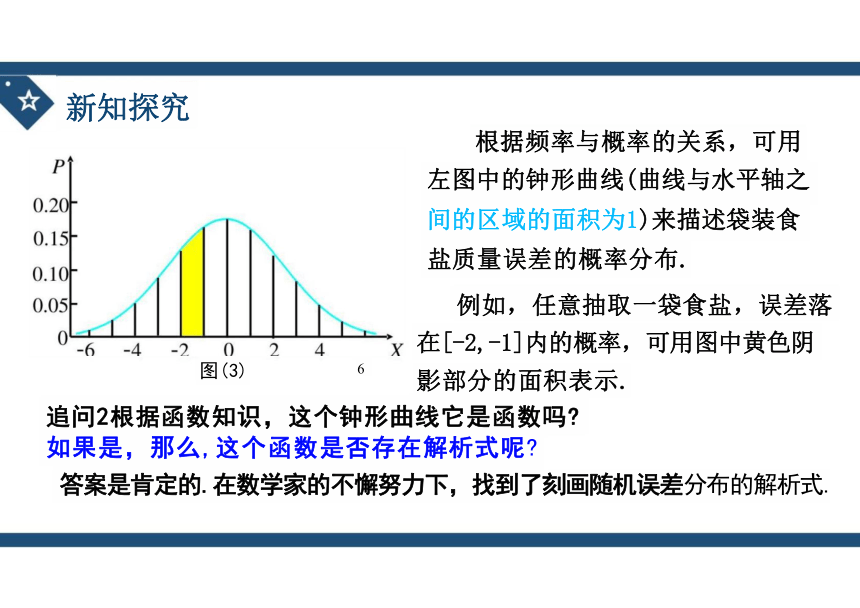
根据频率与概率的关系,可用
左图中的钟形曲线(曲线与水平轴之 间的区域的面积为1)来描述袋装食 盐质量误差的概率分布.
例如,任意抽取一袋食盐,误差落 在[-2,-1]内的概率,可用图中黄色阴 影部分的面积表示.
追问2根据函数知识,这个钟形曲线它是函数吗
如果是,那么,这个函数是否存在解析式呢
答案是肯定的.在数学家的不懈努力下,找到了刻画随机误差分布的解析式.
新知探究
图(3) 6
其中μ∈R ,σ>0 为参数.
显然,对任意的x∈R,f(x)>0, 它的图象在x轴 的上方,可以证明x轴和曲线之间的区域的面积为1. 我们称f(x)为正态密度函数,称它的图象为正态密 度曲线,简称正态曲线,若随机变量X的概率分布 密度函数为f(x), 则称随机变量X服从正态分布,记 为X~N(μ,σ ).
特别地,当μ=0,σ=1时,称随机变量X服从标准正态分布.
概念生成
正态分布
相关知识
早在1733年,法国数学家棣莫弗(A. De Moivre,1667-1754)在研究二项概率的 近似计算时,已提出了正态密度函数的形式,但当时只是作为一个数学表达式.直到 德国数学家高斯(C.F.Gauss ,1777-1855)提出"正态误差"的理论后,正态密度函数 才取得"概率分布"的身份.因此,人们也称正态分布为高斯分布.
高斯是一个伟大的数学家,一生中的重要贡献不胜枚举,早期德国的10马克纸币上 印有高斯的头像和正态分布曲线,这就传达了一个信息:在高斯的科学贡献中,对人 类文明影响最大的是“正态分布”。
新知探究
追问3正态分布曲线是如何刻画随机变量的概率分布的呢
若X~N(μ,σ ),则如右图所示,
X取值不超过x 的概率P(X≤x)为图中区域A的面积, 而P(a≤X≤b)为区域B的面积.
面积即为概率!
新知探究
问题2观察正态曲线及相应的密度函数,你能发现正态曲线的哪些特点
具有两头低、中间高、
左右对称的基本特征
由X 的密度函数及图象可以发现,正态曲线还有以下特点:
(1)曲线是单峰的,它关于直线x=μ对称;
(2)曲线在x=μ处达到峰值(最高点)
(3)正态曲线在x轴上方,两侧与x轴无限接近而不相交;
(4)x轴和曲线之间的区域的面积为1.
新知探究
问题3一个正态分布由参数μ和σ完全确定,这两个参数对正态曲线的形 状有何影响 它们反映正态分布的哪些特征
(1).当参数σ取定值时,μ μ对正态分布的曲线。 由于正态曲线关于x=μ对
称,因此,当参数σ固定时,
0
察
正态曲线的位置由μ确定,且 随着μ的变化而沿x轴平移,
规律:左“-”右“+”
所以参数μ反映了正态分布
的集中位置,可以用均值来估 计,故有E(X)=μ.
故μ 称为位置参数
H
σ=0.5
H
μ=-1 μ=1
μ
新知探究
问题3一个正态分布由参数μ和σ完全确定,这两个参数对正态曲线的形 状有何影响 它们反映正态分布的哪些特征
(2).当参数μ 取定值时,观察σ对正态曲线的影响
μ=0 当μ固定时,因为正态曲线的峰值
σ越大,曲线越“矮 胖”,
表示总体的分布越分散;
σ越小,曲线越“瘦高”,
表示总体的分布越集中.
所以σ反映了随机变量的分布相对 于均值μ的离散程度,可以用标准差 来估计,故有D(X)=o .
故σ称为形状参数 o=0.5
o=1
成反比,而且对任意的σ>0,正态曲线与x 轴之间的区域的面积总为1.
o=2
归纳总结
正态曲线的性质:
(1)曲线在x轴的上方,与x轴不相交;
(2)曲线是单峰的,它关于直线x=μ对称,且在x=μ 处取得最大值
(3)曲线与x轴之间的面积为1;
(4)当μ一定时,o 越大,曲线越“矮胖”,表示总体的分布越分散; σ越小,曲线越“瘦高”,表示总体的分布越集中.
(5)参数μ反映了正态分布的集中位置,σ反映了随机变量的分布相对于 均值μ的离散程度.
在实际问题中,参数 μ, σ 可以分别用样本均值和样本标准差来估计, 故 有 若X~N(μ,σ ), 则E(X)=μ,D(X)=σ .
典例解析
例李明上学有时坐公交车,有时骑自行车,他各记录了50次坐公交车和 骑自行车所花的时间,经数据分析得到:坐公交车平均用时30 min, 样 本 方差为36;骑自行车平均用时34 min, 样本方差为4.假设坐公交车用时X 和骑自行车用时Y都服从正态分布.
(1)估计X,Y 的分布中的参数;
(2)根据(1)中的估计结果,利用信息技术工具画出X 和Y 的分布密度曲线;
(3)如果某天有38 min 可用,李明应选择哪种交通工具 如果某天只有34 min可用,又应该选择哪种交通工具 请说明理由.
分析:对于第(1)问,正态分布由参数μ和σ完全确定,根据正态分布参数的 意义,可以分别用样本均值和样本标准差来估计.
对于第(3)问,这是一个概率决策问题,首先要明确决策的准则,在给定的时 间内选择不迟到概率大的交通工具;然后结合图形,根据概率的表示,比 较概率的大小,作出判断.
解:(1)随机变量X的样本均值为30,样本标准差为6;
随机变量Y的样本均值为34,样本标准差为2.
用样本均值估计参数μ,用样本标准差估计参数σ,可以得到
X~N(30,62),Y~N(34,2 ) .
(2)由(1)得X~N(30,6 ),Y~N(34,22),
作出X和Y的分布密度曲线如图示.
(3)应选择在给定时间内不迟到的概率大的交
通工具。由图可知,
P(X≤38)P(Y≤34).
所以,如果有38 min 可用,那么骑自行车不迟到的概率大,应选择骑自行车; 如果只有34 min可用,那么坐公交车不迟到的概率大,应选择坐公交车.
典例解析
新知探究
正态曲线下的面积规律
正态曲线下对称区域的面积相等一→对应的概率也相等
利用“对称法”求正态分布下随机变量在某个区间的概率
1.若X~N(2,32), 则E(X)= 2 ,D(X)= 9
2.X~N(μ,σ ), 若E(X)=3,σ(X)=2, 则μ= 3 , o
3.若X~N(1,σ ), 且P(X<0)=a, 则
(1)P(X>1)= 0.5 ;(2)P(X>0)= 1-a ;
(3)P(X>2)= a ;(4)P(X<2)= 1-a ;
(5)P(0关键: 画 出正
●
●
巩固练习 课本87页
2. 设随机变量X~N(0,2 ), 随机变量Y~N(0,32), 画出分布密度曲线草图, 并指出P(X≤-2)与P(X≤2)的关系,以及P(|X≤1)与P(|Y≤1)之间的大小关系.
解:作出分布密度曲线如图示,由图可知,
P(X≤-2)+P(X≤2)=1.
P(|X≤1)>P(|Y≤1).
有关的定值.
P(μ-σ≤X≤μ+σ)≈0.6827,
P(μ-2o≤X≤μ+2σ)≈0.9545,
P(μ-3σ≤X≤μ+3σ)≈0.9973.
由此看到,尽管正态变量的取值范围
是(-00,+0o),但在一次试验中,X 的取值几 乎总是落在区间[μ-3σ,μ+3σ]内,而在此 区间以外取值的概率大约只有0.0027, 通 常认为这种情况几乎不可能发生.
新知探究
特殊区间的概率
假设X~N(μ,o ),可以证明:对给定的k∈N*,P(μ-ko≤X≤u+ko)是一个只与k
在实际应用中,通常认为
服从于正态分布N(μ,σ )的随 机变量X 只取[μ-3o,μ+3o]中的 值,这在统计学中称为3σ原则.
μ+o
…68.27%…
.99.73%…
μ +2σ μ +3σ
μ-3σ μ-2o
μ+
新知探究
例在某次数学考试中,考生的成绩X服从正态分布X~N(90,100).
(1).求考试成绩X位于区间(70,110)上的概率是多少
(2).若此次考试共有2000名考生,试估计考试成绩在(80,100)间的考生大约有 多少人
解(1)依题意,X~N(90,100),∴μ=90,σ=10.
P(70≤X≤110)=P(μ-2σ(2)P(80≤X≤100) = P(μ- σ即考试成绩在(80,100)间的概率为0.6827.
考试成绩在(80,100)间的考生大约有2000×0.6827≈1365
巩固练习
则X的
P(X≤0)= 0.5 ,P(IX≤1)= 0.6827 ,
P(X≤1)=0.84135 ,P(X>1)= 0 .15865 (精确 到0.0001.)
课本87页
巩固练习
某厂生产的“T”形零件的外直径(单位: cm)X~N(10,0.22), 某天从该厂
生产的“T”形零件中随机取出两个,测得它们的外直径分别为9.52cm 和 9.98cm , 试分析该厂这一天的生产状况是否正常.
解 :正态变量几乎总是落在区间[μ-3σ,μ+3o]内,所以可通过判断
取出的产品的外直径是否落在这一区间内来分析生产状况是否正常.
∵X~N(10,0.22),∴μ+3σ=10.6,μ—3σ=9.4,
∵9.52∈[9.4,10.6],9.98∈[9.4,10.6],
∴该厂这一天的生产状况是正常的.
说 明:解题时,应当注意零件尺寸应落在[μ-3σ,μ+3σ]之内,否则可以认为该 批产品不合格.判断的根据是概率较小的事件在一次试验中几乎是不可能发生 的,而一旦发生了,就可以认为这批产生不合格.
1.正态分布:
正 太 密 数 。
L 文 效
若随机变量X的概率分布密度函数为f(x), 则称随机变量X服从正态分布,记
为X~N(μ,σ ) .特别地,当μ=0,σ=1时,称随机变量X服从标准正态分布.
2.特殊区间的概率:
P(μ-σ≤X≤μ+σ)≈0.6827,
P(μ-2o≤X≤μ+2σ)≈0.9545,
P(μ-3σ≤X≤μ+3σ)≈0.9973.
课堂小结
End of course
课 程 结 束
第七章 随机变量及其分布
7.5 正态分布
高中数学人教A版(2019)选择性必修第三
复习回顾
回顾前面已经研究过哪些重要的离散型随机变量
二项分布:
一般地,在n重伯努利试验中,设每次试验中事件A发生的概率为p (0
如果随机变量X的分布列具有上式的形式,则称随机变量X服从二项分布 ,记作X~B(n,p).
二项分布的均值与方差:
若X~B(n,p), 则有
E(X)= np ,D(X)= np(1-p) .
复习回顾
回顾前面已经研究过哪些重要的离散型随机变量
超几何分布及其分布列
一般地,假设一批产品共有N件,其中有M件次品.从N件产品中随机 抽取n件(不放回),用X 表示抽取的n件产品中的次品数,则X 的分布列为
,k=m,m+1,m+2,..,r.
超几何分布的均值与方差
E(X)=mp(其中 、
新课导入
现实中,还有大量问题中的随机变量不是离散的,例如
在生产中,在正常生产条件下各种产品的质量指标(如零件的尺寸、维的 纤度等);
在测量中,长度测量误差,某一地区同年龄人群的身高、体重等;
在生物学中,一定条件下生长的小麦的株高、穗长、单位面积产量等; 在气象中,某地每年七月份的平均气温、平均湿度以及降雨量等;
它们的取值往往充满某个区间甚至整个实轴,但取一点的概率为0,我
们称这类随机变量为连续性随机变量,这就是我们所要学习的正态分布。
☆ 新知探究
问题1自动流水线包装的食盐,每袋标准质量为400g.由于各种不可控制的因 素,任意抽取一袋食盐,它的质量与标准质量之间或多或少会存在一定的误差 (实际质量减去标准质量).用X表示这种误差,则X是一个连续型随机变量.检测 人员在一次产品检验中,随机抽取了100袋食盐,获得误差X(单位:g) 的观测 值如下:
(1)如何描述这
100个样本误差
数据的分布
(2)如何构建适 当的概率模型
刻画误差X的
分布
1.4 0.1
0.6 1.7
-1.91.7
-0.5 -1.3
0.3 -1.8
1.1 2.2
0.3 -2.4
-1.8 -3.1
3.8 1.4
1.0 1.3
-0.6 -1.4
-2.6 -3.4
0.5 -3.7
2.6 -2.0
2.4 -1.5
3.5 -4.2
-4.4 -1.1
-0.5 -0.8
2.2 0.3
-2.2 -0.7
-0.2 -0.4 -1.0 3.9 1.7 4.8 -1.3
1.8
3.8
-0.2
-1.0
1.4
-0.8
1.5
-2.9
-1.7
-3.0
-0.7
-0.1
0.1
-0.6
4.4
-3.5
-1.5
-5.2
2.9
-2.6
-1.3
1.5
0.9
1.7
1.2
-2.7
-2.2
0.9
1.2
0.4
-2.1
2.5
-0.6
-1.7
-1.6
-0.9
-0.9
4.4
2.9
2.6
0.2
0.0
0.9
-0.1
-2.1
-3.5
1.7
-0.7 3.3
-0.7 -3.2
2.71.1
根据已学的统计知识,可用频率分布 直方图描述这组误差数据的分布,如图(1) 所示.
频率分布直方图中每个小矩形的面积
表示误差落在相应区间内的频率,所有小 矩形的面积之和为1.
观察图形可知:误差观测值有正有负, 并大致对称地分布在X=0的两侧,而且小误 差比大误差出现得更频繁.
新知探究
(1)如何描述这100个样本误差数据的分布
(2)如何构建适当的概率模型刻画误差X 的分布
频率/组距
-6 -4 -20246 X
图(1)
0.20
0.15 0.10 0.05 0
新知探究
追问1随着样本数据量越来越大,让分组越来越多,组距越来越小,频率
随着样本数据量越来越大,让
分组越来越多,组距越来越小,
由频率的稳定性可知,频率分布 直方图的轮廓就越来越稳定,接 近一条光滑的钟形曲线.
分布直方图的轮廓会发生什么变化
根据频率与概率的关系,可用
左图中的钟形曲线(曲线与水平轴之 间的区域的面积为1)来描述袋装食 盐质量误差的概率分布.
例如,任意抽取一袋食盐,误差落 在[-2,-1]内的概率,可用图中黄色阴 影部分的面积表示.
追问2根据函数知识,这个钟形曲线它是函数吗
如果是,那么,这个函数是否存在解析式呢
答案是肯定的.在数学家的不懈努力下,找到了刻画随机误差分布的解析式.
新知探究
图(3) 6
其中μ∈R ,σ>0 为参数.
显然,对任意的x∈R,f(x)>0, 它的图象在x轴 的上方,可以证明x轴和曲线之间的区域的面积为1. 我们称f(x)为正态密度函数,称它的图象为正态密 度曲线,简称正态曲线,若随机变量X的概率分布 密度函数为f(x), 则称随机变量X服从正态分布,记 为X~N(μ,σ ).
特别地,当μ=0,σ=1时,称随机变量X服从标准正态分布.
概念生成
正态分布
相关知识
早在1733年,法国数学家棣莫弗(A. De Moivre,1667-1754)在研究二项概率的 近似计算时,已提出了正态密度函数的形式,但当时只是作为一个数学表达式.直到 德国数学家高斯(C.F.Gauss ,1777-1855)提出"正态误差"的理论后,正态密度函数 才取得"概率分布"的身份.因此,人们也称正态分布为高斯分布.
高斯是一个伟大的数学家,一生中的重要贡献不胜枚举,早期德国的10马克纸币上 印有高斯的头像和正态分布曲线,这就传达了一个信息:在高斯的科学贡献中,对人 类文明影响最大的是“正态分布”。
新知探究
追问3正态分布曲线是如何刻画随机变量的概率分布的呢
若X~N(μ,σ ),则如右图所示,
X取值不超过x 的概率P(X≤x)为图中区域A的面积, 而P(a≤X≤b)为区域B的面积.
面积即为概率!
新知探究
问题2观察正态曲线及相应的密度函数,你能发现正态曲线的哪些特点
具有两头低、中间高、
左右对称的基本特征
由X 的密度函数及图象可以发现,正态曲线还有以下特点:
(1)曲线是单峰的,它关于直线x=μ对称;
(2)曲线在x=μ处达到峰值(最高点)
(3)正态曲线在x轴上方,两侧与x轴无限接近而不相交;
(4)x轴和曲线之间的区域的面积为1.
新知探究
问题3一个正态分布由参数μ和σ完全确定,这两个参数对正态曲线的形 状有何影响 它们反映正态分布的哪些特征
(1).当参数σ取定值时,μ μ对正态分布的曲线。 由于正态曲线关于x=μ对
称,因此,当参数σ固定时,
0
察
正态曲线的位置由μ确定,且 随着μ的变化而沿x轴平移,
规律:左“-”右“+”
所以参数μ反映了正态分布
的集中位置,可以用均值来估 计,故有E(X)=μ.
故μ 称为位置参数
H
σ=0.5
H
μ=-1 μ=1
μ
新知探究
问题3一个正态分布由参数μ和σ完全确定,这两个参数对正态曲线的形 状有何影响 它们反映正态分布的哪些特征
(2).当参数μ 取定值时,观察σ对正态曲线的影响
μ=0 当μ固定时,因为正态曲线的峰值
σ越大,曲线越“矮 胖”,
表示总体的分布越分散;
σ越小,曲线越“瘦高”,
表示总体的分布越集中.
所以σ反映了随机变量的分布相对 于均值μ的离散程度,可以用标准差 来估计,故有D(X)=o .
故σ称为形状参数 o=0.5
o=1
成反比,而且对任意的σ>0,正态曲线与x 轴之间的区域的面积总为1.
o=2
归纳总结
正态曲线的性质:
(1)曲线在x轴的上方,与x轴不相交;
(2)曲线是单峰的,它关于直线x=μ对称,且在x=μ 处取得最大值
(3)曲线与x轴之间的面积为1;
(4)当μ一定时,o 越大,曲线越“矮胖”,表示总体的分布越分散; σ越小,曲线越“瘦高”,表示总体的分布越集中.
(5)参数μ反映了正态分布的集中位置,σ反映了随机变量的分布相对于 均值μ的离散程度.
在实际问题中,参数 μ, σ 可以分别用样本均值和样本标准差来估计, 故 有 若X~N(μ,σ ), 则E(X)=μ,D(X)=σ .
典例解析
例李明上学有时坐公交车,有时骑自行车,他各记录了50次坐公交车和 骑自行车所花的时间,经数据分析得到:坐公交车平均用时30 min, 样 本 方差为36;骑自行车平均用时34 min, 样本方差为4.假设坐公交车用时X 和骑自行车用时Y都服从正态分布.
(1)估计X,Y 的分布中的参数;
(2)根据(1)中的估计结果,利用信息技术工具画出X 和Y 的分布密度曲线;
(3)如果某天有38 min 可用,李明应选择哪种交通工具 如果某天只有34 min可用,又应该选择哪种交通工具 请说明理由.
分析:对于第(1)问,正态分布由参数μ和σ完全确定,根据正态分布参数的 意义,可以分别用样本均值和样本标准差来估计.
对于第(3)问,这是一个概率决策问题,首先要明确决策的准则,在给定的时 间内选择不迟到概率大的交通工具;然后结合图形,根据概率的表示,比 较概率的大小,作出判断.
解:(1)随机变量X的样本均值为30,样本标准差为6;
随机变量Y的样本均值为34,样本标准差为2.
用样本均值估计参数μ,用样本标准差估计参数σ,可以得到
X~N(30,62),Y~N(34,2 ) .
(2)由(1)得X~N(30,6 ),Y~N(34,22),
作出X和Y的分布密度曲线如图示.
(3)应选择在给定时间内不迟到的概率大的交
通工具。由图可知,
P(X≤38)
所以,如果有38 min 可用,那么骑自行车不迟到的概率大,应选择骑自行车; 如果只有34 min可用,那么坐公交车不迟到的概率大,应选择坐公交车.
典例解析
新知探究
正态曲线下的面积规律
正态曲线下对称区域的面积相等一→对应的概率也相等
利用“对称法”求正态分布下随机变量在某个区间的概率
1.若X~N(2,32), 则E(X)= 2 ,D(X)= 9
2.X~N(μ,σ ), 若E(X)=3,σ(X)=2, 则μ= 3 , o
3.若X~N(1,σ ), 且P(X<0)=a, 则
(1)P(X>1)= 0.5 ;(2)P(X>0)= 1-a ;
(3)P(X>2)= a ;(4)P(X<2)= 1-a ;
(5)P(0
●
●
巩固练习 课本87页
2. 设随机变量X~N(0,2 ), 随机变量Y~N(0,32), 画出分布密度曲线草图, 并指出P(X≤-2)与P(X≤2)的关系,以及P(|X≤1)与P(|Y≤1)之间的大小关系.
解:作出分布密度曲线如图示,由图可知,
P(X≤-2)+P(X≤2)=1.
P(|X≤1)>P(|Y≤1).
有关的定值.
P(μ-σ≤X≤μ+σ)≈0.6827,
P(μ-2o≤X≤μ+2σ)≈0.9545,
P(μ-3σ≤X≤μ+3σ)≈0.9973.
由此看到,尽管正态变量的取值范围
是(-00,+0o),但在一次试验中,X 的取值几 乎总是落在区间[μ-3σ,μ+3σ]内,而在此 区间以外取值的概率大约只有0.0027, 通 常认为这种情况几乎不可能发生.
新知探究
特殊区间的概率
假设X~N(μ,o ),可以证明:对给定的k∈N*,P(μ-ko≤X≤u+ko)是一个只与k
在实际应用中,通常认为
服从于正态分布N(μ,σ )的随 机变量X 只取[μ-3o,μ+3o]中的 值,这在统计学中称为3σ原则.
μ+o
…68.27%…
.99.73%…
μ +2σ μ +3σ
μ-3σ μ-2o
μ+
新知探究
例在某次数学考试中,考生的成绩X服从正态分布X~N(90,100).
(1).求考试成绩X位于区间(70,110)上的概率是多少
(2).若此次考试共有2000名考生,试估计考试成绩在(80,100)间的考生大约有 多少人
解(1)依题意,X~N(90,100),∴μ=90,σ=10.
P(70≤X≤110)=P(μ-2σ
考试成绩在(80,100)间的考生大约有2000×0.6827≈1365
巩固练习
则X的
P(X≤0)= 0.5 ,P(IX≤1)= 0.6827 ,
P(X≤1)=0.84135 ,P(X>1)= 0 .15865 (精确 到0.0001.)
课本87页
巩固练习
某厂生产的“T”形零件的外直径(单位: cm)X~N(10,0.22), 某天从该厂
生产的“T”形零件中随机取出两个,测得它们的外直径分别为9.52cm 和 9.98cm , 试分析该厂这一天的生产状况是否正常.
解 :正态变量几乎总是落在区间[μ-3σ,μ+3o]内,所以可通过判断
取出的产品的外直径是否落在这一区间内来分析生产状况是否正常.
∵X~N(10,0.22),∴μ+3σ=10.6,μ—3σ=9.4,
∵9.52∈[9.4,10.6],9.98∈[9.4,10.6],
∴该厂这一天的生产状况是正常的.
说 明:解题时,应当注意零件尺寸应落在[μ-3σ,μ+3σ]之内,否则可以认为该 批产品不合格.判断的根据是概率较小的事件在一次试验中几乎是不可能发生 的,而一旦发生了,就可以认为这批产生不合格.
1.正态分布:
正 太 密 数 。
L 文 效
若随机变量X的概率分布密度函数为f(x), 则称随机变量X服从正态分布,记
为X~N(μ,σ ) .特别地,当μ=0,σ=1时,称随机变量X服从标准正态分布.
2.特殊区间的概率:
P(μ-σ≤X≤μ+σ)≈0.6827,
P(μ-2o≤X≤μ+2σ)≈0.9545,
P(μ-3σ≤X≤μ+3σ)≈0.9973.
课堂小结
End of course
课 程 结 束
