3.3幂函数 课件(共32张PPT) 高中数学人教A版(2019)必修1
文档属性
| 名称 | 3.3幂函数 课件(共32张PPT) 高中数学人教A版(2019)必修1 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-22 00:00:00 | ||
图片预览






文档简介
(共32张PPT)
3.3幂函数
高一上数学
新知探究
前面学习了函数的概念,利用函数概念和对函数的观察,研究了函数 的一些性质.本节我们利用这些知识研究一类新的函数.先看几个实例.
(1)如果张红以1元/kg的价格购买了某种蔬菜wkg, 那么她需要支付 p=w 元,这里p是w 的函数;
(2)如果正方形的边长为a, 那么正方形的面积S=a , 这里S是a 的函数;
(3)如果立方体的棱长为b, 那么立方体的体积V=b , 这里V是b的函数;
(4)如果一个正方形场地的面积为S,那么这个正方形场地的边长c=√S, 这里c是S的函数;
(5)如果某人t s内骑车行进了1km, 那么他骑车的平均速度 即v=t-1, 这里v是t的函数.
新知探究
活动1:请观察(1)-(5)中的函数解析式,讨论它们有何共同特征.
(1)p=w;
(2)S=a ;
(3)V=b ;
(4)c= √S, 即 ;
(5) 即v=t-1.
解析式都有幂的形式
都是以幂的底数为自变量
幂的指数都是常数
y=X
y=x y=x
y=x“
新知生成
一 、幂函数的定义
一般地,函数y=xa 叫做幂函数,其中x 是自变量,α是常数.
牛刀小试:下列函数是幂函数的是(①⑥⑦)
②y =(x+1) ③y=2× ④y =3x
⑤y=x+1 ⑥y=x , ⑦y=x
★(1)底数只能为自变量x;
(2)指数是常数;
(3)xα的系数为1;
(4)项数只有一项。
y
3
2
y
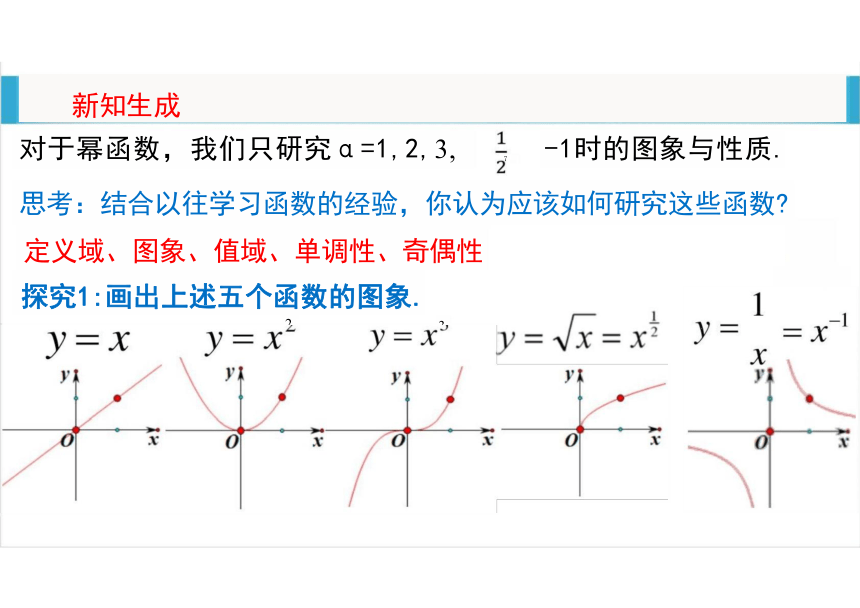
对于幂函数,我们只研究α=1,2,3, 7 -1时的图象与性质.
思考:结合以往学习函数的经验,你认为应该如何研究这些函数
新知生成
定义域、图象、值域、单调性、奇偶性
探究1:画出上述五个函数的图象.
∵x 一X <0,√x +√x >0,
∴f(x )课后练习:证明f(x)=x 的单调性和奇偶性.
新知生成
研究幂函数f(x)=√x 的图象画法.
单调性证明:函数的定义域是[0,+0].
Vx ,x ∈[0,+0],且xy=x y=x y=x y=x2
y=x-1
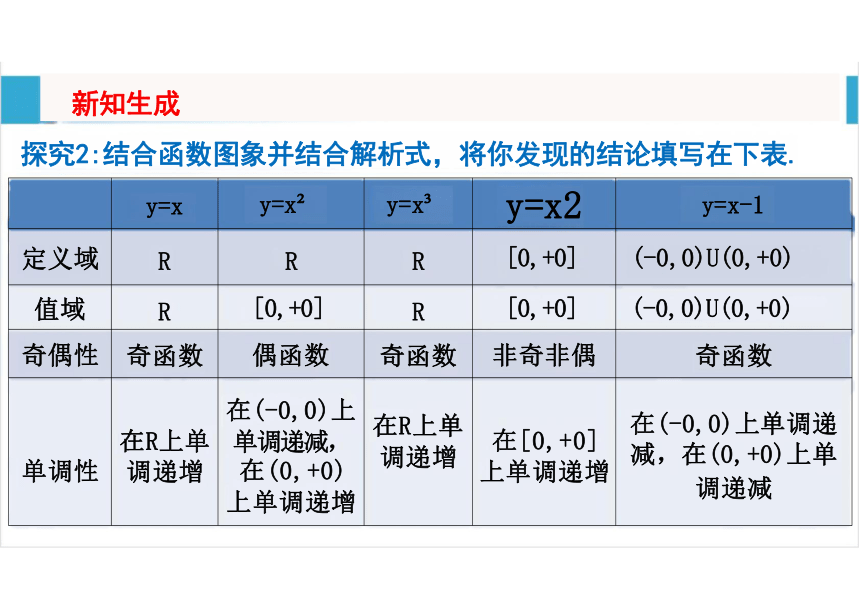
定义域 R R R [0,+0]
(-0,0)U(0,+0)
值域 R [0,+0] R [0,+0]
(-0,0)U(0,+0)
奇偶性 奇函数 偶函数 奇函数 非奇非偶
奇函数
单调性 在R上单 调递增 在(-0,0)上 单调递减, 在(0,+0) 上单调递增 在R上单 调递增 在[0,+0] 上单调递增
在(-0,0)上单调递
减,在(0,+0)上单
调递减
新知生成
探究2:结合函数图象并结合解析式,将你发现的结论填写在下表.
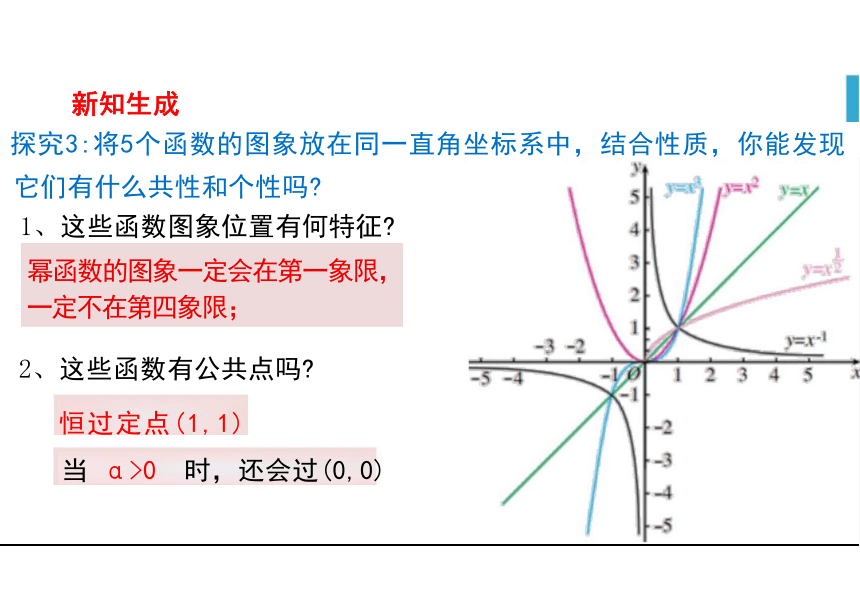
幂函数的图象一定会在第一象限, 一定不在第四象限;
它们有什么共性和个性吗
1、这些函数图象位置有何特征
探究3:将5个函数的图象放在同一直角坐标系中,结合性质,你能发现
当 α>0 时,还会过(0,0)
2、这些函数有公共点吗
恒过定点(1,1)
新知生成
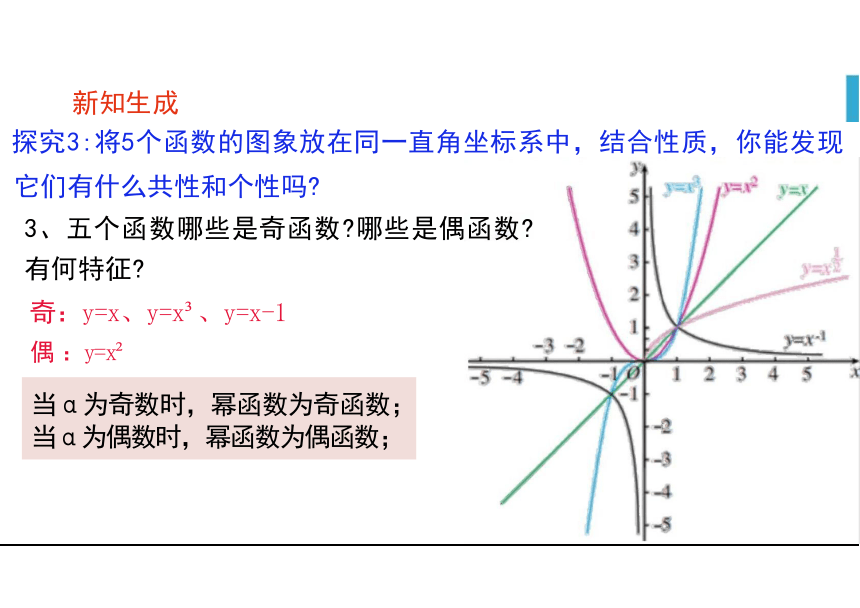
它们有什么共性和个性吗
3、五个函数哪些是奇函数 哪些是偶函数
有何特征
奇:y=x、y=x 、y=x-1
偶 :y=x
当α为奇数时,幂函数为奇函数; 当α为偶数时,幂函数为偶函数;
探究3:将5个函数的图象放在同一直角坐标系中,结合性质,你能发现
新知生成
当 α>0 时,函数在[0,+0]上是增函数;
当 α<0 时,函数在[0,+0]上是减函数; 当α<0 时,函数在(0,+0)上无单调性
新知生成
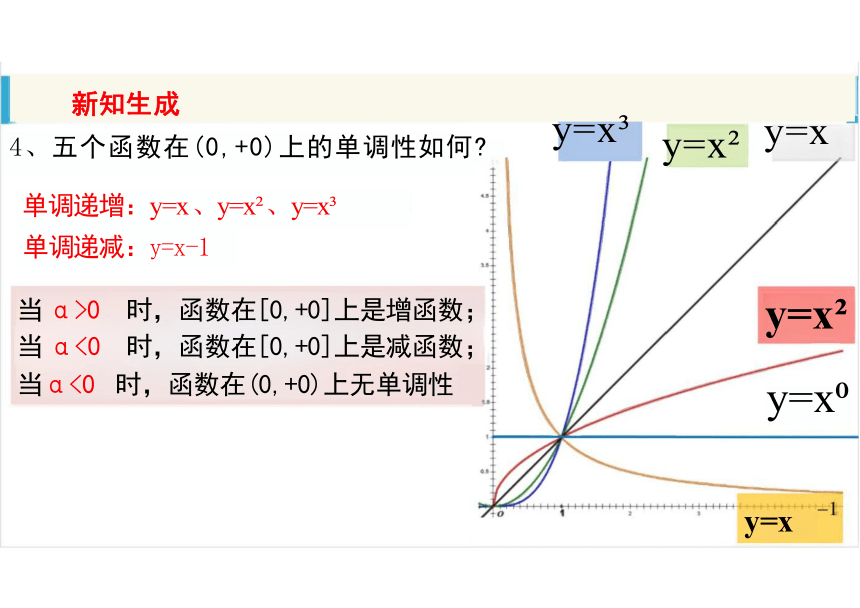
4、五个函数在(0,+0)上的单调性如何 y=x y=x y=x
单调递增:y=x 、y=x 、y=x
单调递减:y=x-1
y=x
y=x
y=x
新知生成
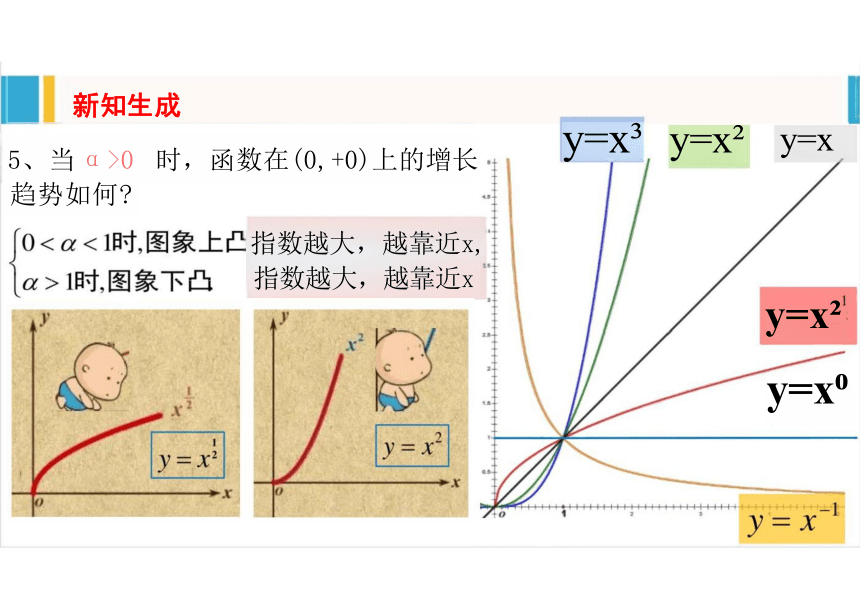
5、当 α>0 时,函数在(0,+0)上的增长
趋势如何
指数越大,越靠近x, 指数越大,越靠近x
y=x y=x y=x
y=x
y=x
概念辨析
练习:下列说法正确的为(D )
①幂函数的图象不可能在第四象限;
②n=0, 函数y=xn 的图象是一条直线;
③幂函数y=xn 当 n>0 时,是增函数;
④幂函数y=xn 当 n<0 时,在第一象限内函数值随x 值的增大而减小.
A.②③ B.③④ C.①② D.①④
解析:当n=0 时,y=x”的图象为除去一点的直线,②错误;y=x 不是增函
数,③错误,①④显然正确.故选D.
1, 1 1, 2, 3
练习:已知 2
若幂函数f(x)=xα为奇函数,且在(0,十一)上递减,则 α=-1
1
题型一:求幂函数解析式
例题(教材P91-1): 已知幂函数f(x) 的图象过点(2,√2),求f(x)的解析式.
解:由m -m-1=1 得m=2 或m=-1. m=2 时,f(x)=x , 符合题意
m=-1 时, ,不符合题意
∴f(x)=x ,x∈R.
解:设f(x)=x",∵2 = √2=2 ,:
∴f(x)=x =√x,x∈[0,+00].
练习:若f(x)=(m -m-1)xm +m-3是幂函数,且x>0时f(x)是增函数,求f(x).
●
题型二:幂函数图象与性质
练习:函数 的图象大致是( D )
A B C D
题型二:幂函数图象与性质
例题:如图所示,曲线是幂函数y=xa 在第一象限内的图象,已知α分别取
—1,1, 7 2四个值,则图象C ,C ,C ,C 对应的α依次为 2,1,2,-1
则与曲线C ,C ,C ,C4
A.2, ,—2
B.—2, ,2 C. ,—2,2, D.2, ,—2,
练习:如图是幂函数y=xn 的部分图象,已知n 取 ,2, 2,
这四个值,
相对应的n 依次为(A)
y=xa
y=xb
y=xC
y=xd
3
图象如图所示,则a,b,c,d的大小关系是B( )
A.d>c>b>a B.a>b>c>d
C.d>c>a>b D.a> >d>C
在(1,+0)上,指大图高
在(0,1)上,指大图低
推广:若四个幂函数图象y =xa,y=x b,y=xC,y=xd 在同一坐标系中的
练习:在同一坐标系内y=x (a≠0)和 的图象可能是
A
D
B
题型三:比较大小
例题:比较下列各组数中两个数的大小.
(1) 与 ;
解:(1)∵幂函数y =x .5在(0,+0)上是单调递增的,
,∴
(2)∵幂函数 在(0,+0)上是单调递减的,
又1 . 1>0 . 9,
(3)∵幂函数 和 在(0,+0)上是单调递增的,
··
9
;
。
练习: 比较大小
(1)1.53 < 1.73
(2)0.15-1 > 0.17-1
(3)2.2-2 < 1.8-2
(4)0.70.5 > 0.72
练习:若(a+1) <(3-2a) , 则实数a的取值范围是 3
[-1,2]
当幂指数相同时,可直接利用幂函数的单调性来比较
当幂指数不同时,可以先转化为相同的幂指数,再利用
单调性来比较大小
当底数不同且幂指数也不同时,不能运用单调性比较大 小,可选取适当的中间值,从而达到比较大小的目的
比较幂的大小的基本方法:
直接法
转化法
中间 量法
课堂小结
结构特征
描点作图
图象异同
不同指数对幂 函数性质的影响
数形结合——研究函数图象和性质 特值法— —取特殊点辨析图象
构造函数法 — — 比较大小
幂函数概念
幂函数图象
幂函数性质
幂函数
思想方法
应 用
作业布置
1.画出函数y=√ |x| 的图象,并判断函数的奇偶性,讨论函数的单调性.
2.利用幂函数的性质,比较下列各题中两个值的大小:
(1)(—1.5) ,(—1.4) ; (2) 心
3.根据单调性和奇偶性的定义证明函数f(x)=x 的单调性和奇偶性.
3.试用描点法画出函数f(x)=x- 的图象,求函数的定义域、值域;讨论函数的单调性、奇偶 性,并证明.
12.试讨论函数 的定义域、值域、单调性、奇偶性,并画出函数图象.
1. 画出函数y=√ |x| 的图象,并判断函数的奇偶性,讨论函数的单调性.
1. 图象略. 函数为偶函数;在(-0,0)上单调递减,在(0,十○)上单调递增
2. (1)(-1.5) <(—1.4) .
作业布置
3.根据单调性和奇偶性的定义证明函数f(x)=x 的单调性和奇偶性.
3.因为f(一x)=(一x) =—x =-f(x), 所以f(x)为奇函数.任取x ,x ∈ R,且x <
因为
所以 f(x )3. 图象略.定义域为(- ○,0)U(0, 十○),值域为(0,十○);函数为偶函数;函数在
(0,十一)上单调递减,在(一○,0)上单调递增.证明略.
作业布置
. 当x ,x ∈(0, 十○)时,x x >0. 又因为x增;当x ,x ∈(-0,0) 时,x x > 0.又因为x 义可得,y=f(x) 在(一○,0)上单调递增. 因此,y=f(x) 在(0,十 一 ),( - 0,0)上都
单调递增. 图略.
12 . 试讨论函数 的定义域、值域、单调性、奇偶性,并画出函数图象 .
12.设y=f(x), 定义域D=(—α,0)U(0, 十○).
所以函数为奇函数.
对于任意的x∈D,
8.证明:
(1)若f(x)=ax+b, 则
(2)若g(x)=x +ax+b,
则
下凸:函数在区间[x,x ]的图象总在线段M M 的下方;
下凸:
函数y=f(x)凸性的几何特征
上凸:函数在区间[x,x ]的图象总在线段M M 的上方;
上凸:
函 数y=f(x)凸性的几何特征
下凸:函数在区间[x,x ]的图象总在线段M M 的下方;
上凸:函数在区间[x,x ]的图象总在线段M M 的上方;
函数y=f(x)凸性的几何特征
3.3幂函数
高一上数学
新知探究
前面学习了函数的概念,利用函数概念和对函数的观察,研究了函数 的一些性质.本节我们利用这些知识研究一类新的函数.先看几个实例.
(1)如果张红以1元/kg的价格购买了某种蔬菜wkg, 那么她需要支付 p=w 元,这里p是w 的函数;
(2)如果正方形的边长为a, 那么正方形的面积S=a , 这里S是a 的函数;
(3)如果立方体的棱长为b, 那么立方体的体积V=b , 这里V是b的函数;
(4)如果一个正方形场地的面积为S,那么这个正方形场地的边长c=√S, 这里c是S的函数;
(5)如果某人t s内骑车行进了1km, 那么他骑车的平均速度 即v=t-1, 这里v是t的函数.
新知探究
活动1:请观察(1)-(5)中的函数解析式,讨论它们有何共同特征.
(1)p=w;
(2)S=a ;
(3)V=b ;
(4)c= √S, 即 ;
(5) 即v=t-1.
解析式都有幂的形式
都是以幂的底数为自变量
幂的指数都是常数
y=X
y=x y=x
y=x“
新知生成
一 、幂函数的定义
一般地,函数y=xa 叫做幂函数,其中x 是自变量,α是常数.
牛刀小试:下列函数是幂函数的是(①⑥⑦)
②y =(x+1) ③y=2× ④y =3x
⑤y=x+1 ⑥y=x , ⑦y=x
★(1)底数只能为自变量x;
(2)指数是常数;
(3)xα的系数为1;
(4)项数只有一项。
y
3
2
y
对于幂函数,我们只研究α=1,2,3, 7 -1时的图象与性质.
思考:结合以往学习函数的经验,你认为应该如何研究这些函数
新知生成
定义域、图象、值域、单调性、奇偶性
探究1:画出上述五个函数的图象.
∵x 一X <0,√x +√x >0,
∴f(x )
新知生成
研究幂函数f(x)=√x 的图象画法.
单调性证明:函数的定义域是[0,+0].
Vx ,x ∈[0,+0],且x
y=x-1
定义域 R R R [0,+0]
(-0,0)U(0,+0)
值域 R [0,+0] R [0,+0]
(-0,0)U(0,+0)
奇偶性 奇函数 偶函数 奇函数 非奇非偶
奇函数
单调性 在R上单 调递增 在(-0,0)上 单调递减, 在(0,+0) 上单调递增 在R上单 调递增 在[0,+0] 上单调递增
在(-0,0)上单调递
减,在(0,+0)上单
调递减
新知生成
探究2:结合函数图象并结合解析式,将你发现的结论填写在下表.
幂函数的图象一定会在第一象限, 一定不在第四象限;
它们有什么共性和个性吗
1、这些函数图象位置有何特征
探究3:将5个函数的图象放在同一直角坐标系中,结合性质,你能发现
当 α>0 时,还会过(0,0)
2、这些函数有公共点吗
恒过定点(1,1)
新知生成
它们有什么共性和个性吗
3、五个函数哪些是奇函数 哪些是偶函数
有何特征
奇:y=x、y=x 、y=x-1
偶 :y=x
当α为奇数时,幂函数为奇函数; 当α为偶数时,幂函数为偶函数;
探究3:将5个函数的图象放在同一直角坐标系中,结合性质,你能发现
新知生成
当 α>0 时,函数在[0,+0]上是增函数;
当 α<0 时,函数在[0,+0]上是减函数; 当α<0 时,函数在(0,+0)上无单调性
新知生成
4、五个函数在(0,+0)上的单调性如何 y=x y=x y=x
单调递增:y=x 、y=x 、y=x
单调递减:y=x-1
y=x
y=x
y=x
新知生成
5、当 α>0 时,函数在(0,+0)上的增长
趋势如何
指数越大,越靠近x, 指数越大,越靠近x
y=x y=x y=x
y=x
y=x
概念辨析
练习:下列说法正确的为(D )
①幂函数的图象不可能在第四象限;
②n=0, 函数y=xn 的图象是一条直线;
③幂函数y=xn 当 n>0 时,是增函数;
④幂函数y=xn 当 n<0 时,在第一象限内函数值随x 值的增大而减小.
A.②③ B.③④ C.①② D.①④
解析:当n=0 时,y=x”的图象为除去一点的直线,②错误;y=x 不是增函
数,③错误,①④显然正确.故选D.
1, 1 1, 2, 3
练习:已知 2
若幂函数f(x)=xα为奇函数,且在(0,十一)上递减,则 α=-1
1
题型一:求幂函数解析式
例题(教材P91-1): 已知幂函数f(x) 的图象过点(2,√2),求f(x)的解析式.
解:由m -m-1=1 得m=2 或m=-1. m=2 时,f(x)=x , 符合题意
m=-1 时, ,不符合题意
∴f(x)=x ,x∈R.
解:设f(x)=x",∵2 = √2=2 ,:
∴f(x)=x =√x,x∈[0,+00].
练习:若f(x)=(m -m-1)xm +m-3是幂函数,且x>0时f(x)是增函数,求f(x).
●
题型二:幂函数图象与性质
练习:函数 的图象大致是( D )
A B C D
题型二:幂函数图象与性质
例题:如图所示,曲线是幂函数y=xa 在第一象限内的图象,已知α分别取
—1,1, 7 2四个值,则图象C ,C ,C ,C 对应的α依次为 2,1,2,-1
则与曲线C ,C ,C ,C4
A.2, ,—2
B.—2, ,2 C. ,—2,2, D.2, ,—2,
练习:如图是幂函数y=xn 的部分图象,已知n 取 ,2, 2,
这四个值,
相对应的n 依次为(A)
y=xa
y=xb
y=xC
y=xd
3
图象如图所示,则a,b,c,d的大小关系是B( )
A.d>c>b>a B.a>b>c>d
C.d>c>a>b D.a> >d>C
在(1,+0)上,指大图高
在(0,1)上,指大图低
推广:若四个幂函数图象y =xa,y=x b,y=xC,y=xd 在同一坐标系中的
练习:在同一坐标系内y=x (a≠0)和 的图象可能是
A
D
B
题型三:比较大小
例题:比较下列各组数中两个数的大小.
(1) 与 ;
解:(1)∵幂函数y =x .5在(0,+0)上是单调递增的,
,∴
(2)∵幂函数 在(0,+0)上是单调递减的,
又1 . 1>0 . 9,
(3)∵幂函数 和 在(0,+0)上是单调递增的,
··
9
;
。
练习: 比较大小
(1)1.53 < 1.73
(2)0.15-1 > 0.17-1
(3)2.2-2 < 1.8-2
(4)0.70.5 > 0.72
练习:若(a+1) <(3-2a) , 则实数a的取值范围是 3
[-1,2]
当幂指数相同时,可直接利用幂函数的单调性来比较
当幂指数不同时,可以先转化为相同的幂指数,再利用
单调性来比较大小
当底数不同且幂指数也不同时,不能运用单调性比较大 小,可选取适当的中间值,从而达到比较大小的目的
比较幂的大小的基本方法:
直接法
转化法
中间 量法
课堂小结
结构特征
描点作图
图象异同
不同指数对幂 函数性质的影响
数形结合——研究函数图象和性质 特值法— —取特殊点辨析图象
构造函数法 — — 比较大小
幂函数概念
幂函数图象
幂函数性质
幂函数
思想方法
应 用
作业布置
1.画出函数y=√ |x| 的图象,并判断函数的奇偶性,讨论函数的单调性.
2.利用幂函数的性质,比较下列各题中两个值的大小:
(1)(—1.5) ,(—1.4) ; (2) 心
3.根据单调性和奇偶性的定义证明函数f(x)=x 的单调性和奇偶性.
3.试用描点法画出函数f(x)=x- 的图象,求函数的定义域、值域;讨论函数的单调性、奇偶 性,并证明.
12.试讨论函数 的定义域、值域、单调性、奇偶性,并画出函数图象.
1. 画出函数y=√ |x| 的图象,并判断函数的奇偶性,讨论函数的单调性.
1. 图象略. 函数为偶函数;在(-0,0)上单调递减,在(0,十○)上单调递增
2. (1)(-1.5) <(—1.4) .
作业布置
3.根据单调性和奇偶性的定义证明函数f(x)=x 的单调性和奇偶性.
3.因为f(一x)=(一x) =—x =-f(x), 所以f(x)为奇函数.任取x ,x ∈ R,且x <
因为
所以 f(x )
(0,十一)上单调递减,在(一○,0)上单调递增.证明略.
作业布置
. 当x ,x ∈(0, 十○)时,x x >0. 又因为x
单调递增. 图略.
12 . 试讨论函数 的定义域、值域、单调性、奇偶性,并画出函数图象 .
12.设y=f(x), 定义域D=(—α,0)U(0, 十○).
所以函数为奇函数.
对于任意的x∈D,
8.证明:
(1)若f(x)=ax+b, 则
(2)若g(x)=x +ax+b,
则
下凸:函数在区间[x,x ]的图象总在线段M M 的下方;
下凸:
函数y=f(x)凸性的几何特征
上凸:函数在区间[x,x ]的图象总在线段M M 的上方;
上凸:
函 数y=f(x)凸性的几何特征
下凸:函数在区间[x,x ]的图象总在线段M M 的下方;
上凸:函数在区间[x,x ]的图象总在线段M M 的上方;
函数y=f(x)凸性的几何特征
