湘教版八年级下册(新)第2章《2.1.2 多边形的外角》课件(14张PPT)
文档属性
| 名称 | 湘教版八年级下册(新)第2章《2.1.2 多边形的外角》课件(14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 596.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-30 15:06:21 | ||
图片预览





文档简介
课件14张PPT。2.1 多边形2 多边形的外角复习:n边形的内角和为_________________.(n-2) 180 °
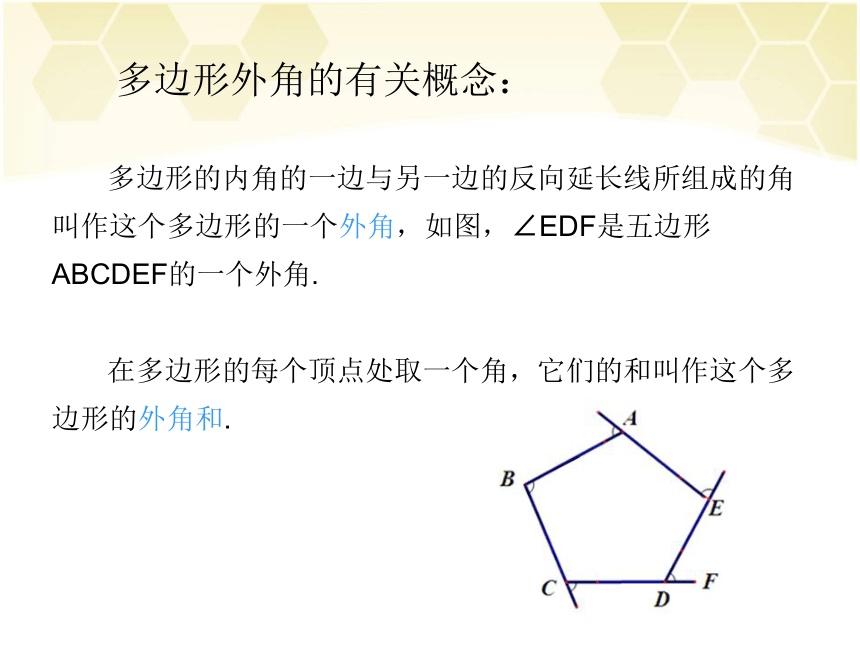
它有什么作用呢?1.知道多边形的边数,可以求出多边形的度数.2.知道多边形的度数,可以求出多边形的边数. 多边形外角的有关概念: 多边形的内角的一边与另一边的反向延长线所组成的角
叫作这个多边形的一个外角,如图,∠EDF是五边形
ABCDEF的一个外角.
在多边形的每个顶点处取一个角,它们的和叫作这个多
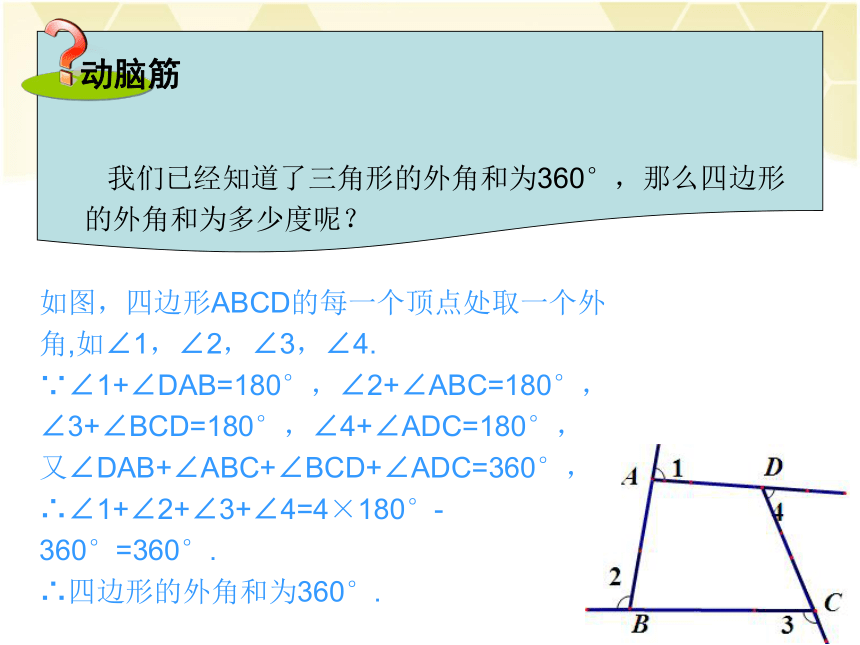
边形的外角和. 我们已经知道了三角形的外角和为360°,那么四边形的外角和为多少度呢?如图,四边形ABCD的每一个顶点处取一个外角,如∠1,∠2,∠3,∠4.
∵∠1+∠DAB=180°,∠2+∠ABC=180°,
∠3+∠BCD=180°,∠4+∠ADC=180°,
又∠DAB+∠ABC+∠BCD+∠ADC=360°,
∴∠1+∠2+∠3+∠4=4×180°-360°=360°.
∴四边形的外角和为360°. 探究 三角形的外角和是360°,四边形的外角和是
360°,n边形(n为不小于3的任何整数)的外角和
都是360°吗?n边形的外角和与边数有关系吗? 类似于求四边形外角和的思路,在n边形的每一个顶点处取
一个外角,其中每个外角与它相邻的内角之和为180°.因此,
这n个外角与跟它相邻的内角之和加起来就是n·180°,将这
个总和减去n边形的内角和(n-2)·180°所得的差即为n边形
的外角和.
n·180°-(n-2)·180°
=[n-(n-2)]·180°
=2×180°
=360°.
由此得出:任意多边形的外角和等于360°. 例 一个多边形的内角和等于它外角和的5倍,它是几边形?解 设多边形的边数为n,则它的内角和为(n-2)·180°.
由题意得
(n-2)·180°=360°×5,
解得 n=12.
因此这个多边形是十二边形. 观察三角形具有稳定型,那么四边形呢?用4根木条钉成如图的木框,任意扭转四边形的边,它的形状会发生变化吗? 我们发现,四边形的边长不变,但它的形状改变了,这
说明四边形具有不稳定性. 图1 图2 图3
在实际生活中,我们经常利用四边形的不稳定性,如上图1中电动伸缩门,图2中的升降机.有时又要克服四边形的不稳定性,例如图3中的栅栏两横梁之间加钉斜木条,构成三角形,这是为了利用三角形的稳定性. 练习 1.一个多边形的每个外角都等于45°,这个多边形是几边
形?它的每一个内角是多少度?解:n=360°÷45°=9,
180°-45°=135°.
答:这个多边形是九边形,它的每个内角是135°. 2.如图,求图中x的值.解:由题意,得
3x+90×2=360.
解得x=60. 3.请举出日常生活中利用四边形不稳定性的一些例子.答:折叠衣架,伸缩尺,立体折叠画等.1.多边形的外角和课堂小结:2.四边形具有不稳定性
它有什么作用呢?1.知道多边形的边数,可以求出多边形的度数.2.知道多边形的度数,可以求出多边形的边数. 多边形外角的有关概念: 多边形的内角的一边与另一边的反向延长线所组成的角
叫作这个多边形的一个外角,如图,∠EDF是五边形
ABCDEF的一个外角.
在多边形的每个顶点处取一个角,它们的和叫作这个多
边形的外角和. 我们已经知道了三角形的外角和为360°,那么四边形的外角和为多少度呢?如图,四边形ABCD的每一个顶点处取一个外角,如∠1,∠2,∠3,∠4.
∵∠1+∠DAB=180°,∠2+∠ABC=180°,
∠3+∠BCD=180°,∠4+∠ADC=180°,
又∠DAB+∠ABC+∠BCD+∠ADC=360°,
∴∠1+∠2+∠3+∠4=4×180°-360°=360°.
∴四边形的外角和为360°. 探究 三角形的外角和是360°,四边形的外角和是
360°,n边形(n为不小于3的任何整数)的外角和
都是360°吗?n边形的外角和与边数有关系吗? 类似于求四边形外角和的思路,在n边形的每一个顶点处取
一个外角,其中每个外角与它相邻的内角之和为180°.因此,
这n个外角与跟它相邻的内角之和加起来就是n·180°,将这
个总和减去n边形的内角和(n-2)·180°所得的差即为n边形
的外角和.
n·180°-(n-2)·180°
=[n-(n-2)]·180°
=2×180°
=360°.
由此得出:任意多边形的外角和等于360°. 例 一个多边形的内角和等于它外角和的5倍,它是几边形?解 设多边形的边数为n,则它的内角和为(n-2)·180°.
由题意得
(n-2)·180°=360°×5,
解得 n=12.
因此这个多边形是十二边形. 观察三角形具有稳定型,那么四边形呢?用4根木条钉成如图的木框,任意扭转四边形的边,它的形状会发生变化吗? 我们发现,四边形的边长不变,但它的形状改变了,这
说明四边形具有不稳定性. 图1 图2 图3
在实际生活中,我们经常利用四边形的不稳定性,如上图1中电动伸缩门,图2中的升降机.有时又要克服四边形的不稳定性,例如图3中的栅栏两横梁之间加钉斜木条,构成三角形,这是为了利用三角形的稳定性. 练习 1.一个多边形的每个外角都等于45°,这个多边形是几边
形?它的每一个内角是多少度?解:n=360°÷45°=9,
180°-45°=135°.
答:这个多边形是九边形,它的每个内角是135°. 2.如图,求图中x的值.解:由题意,得
3x+90×2=360.
解得x=60. 3.请举出日常生活中利用四边形不稳定性的一些例子.答:折叠衣架,伸缩尺,立体折叠画等.1.多边形的外角和课堂小结:2.四边形具有不稳定性
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
