北师大版九年级下册1.1锐角三角函数第一课时课件(共21张PPT)
文档属性
| 名称 | 北师大版九年级下册1.1锐角三角函数第一课时课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-22 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
锐角三角函数
第一课时
1.经历探索直角三角形中边角关系的过程,能说出正切的定义及表示方法,并类比说出正弦、余弦的定义及表示方法,并能够举例说明;
2.能够用 tanA.sinA.cosA表示直角三角形中两直角边的比,并能进行简单计算.
学习目标
整体感知,导入新课
我们在直角三角形中学过哪些关系?
一是直角三角形中边边之间的关系,也就是勾股定理.
二是角角之间的关系,就是直角三角形当中的两个锐角互余.
那么这一章我们将研究什么问题呢?
就是直角三角形中边和角之间的关系。那么在直角三角形中边和角有什么样的关系呢?
整体感知,导入新课
问题1:本节课研究直角三角形的边角关系,想研究边与角的关系,首先需要确定个角,再研究它与两边的关系,前面研究过任意两边的和、差关系,接下来研究比商关系;存在几种两边比商关系
自学与合作
根据特殊,引发猜想
问题2:在直角三角形中,45°角的对边与邻边的比值是多少 改变三角形的大小,这个结论还成立吗
自学与合作
问题3:把直角三角形中这个45°的角换成30°时,它的对边与邻边的比值还是一个固定值吗 改变三角形的大小,这个结论还成立吗 再换成60°呢
在RtΔABC,∠C=90°.
当∠A=45°时,∠A的对边与邻边的比值是固定值1;
当∠A=30°时,∠A的对边与邻边的比值是固定值 ;
当∠A=60°时,∠A的对边与邻边的比值是固定值 .
与三角形的大小无关.
根据特殊,引发猜想
自学与合作
问题4:根据上面的总结,在Rt△ABC中,∠C=90°,当∠A取其它一定度数的锐角时,它的对边与邻边的比值会出现什么情况 对此,你有怎样的猜想
猜想:在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,它的对边与邻边的比也是一个固定值.
验证猜想,形成概念
自学与合作
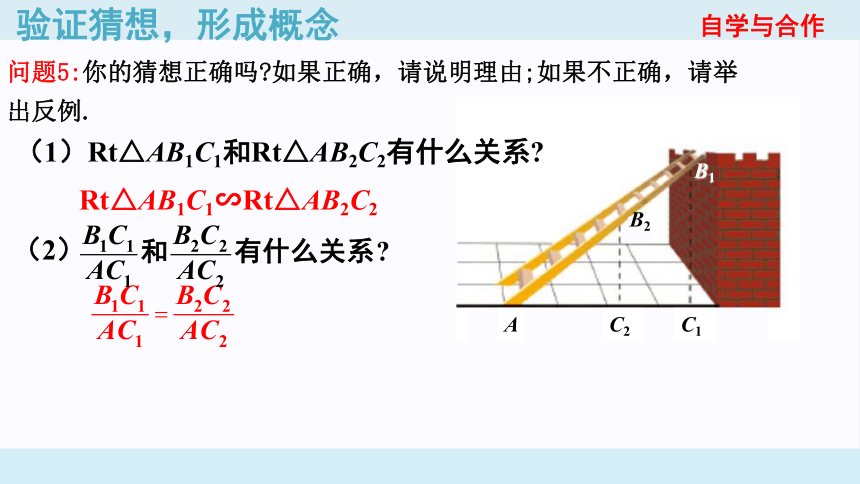
问题5:你的猜想正确吗 如果正确,请说明理由;如果不正确,请举出反例.
A
C2
C1
B1
B2
(1)Rt△AB1C1和Rt△AB2C2有什么关系
Rt△AB1C1∽Rt△AB2C2
(2)
A
C2
C1
B1
B2
B3
C3
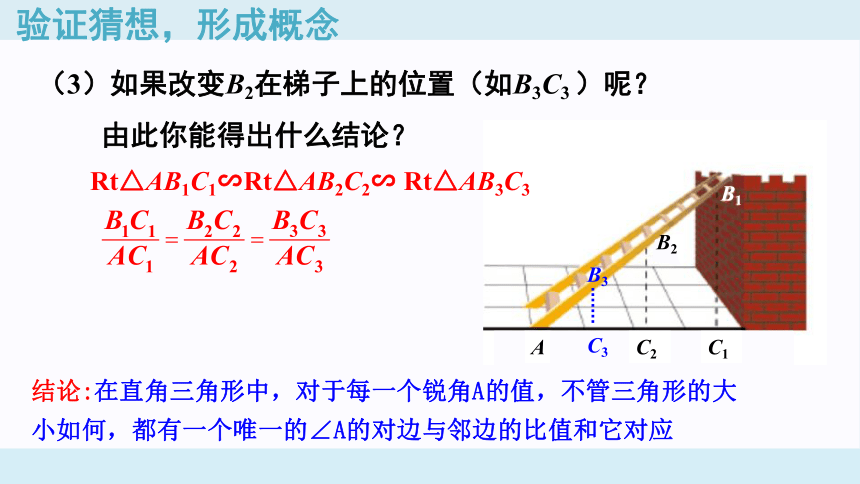
(3)如果改变B2在梯子上的位置(如B3C3 )呢?由此你能得出什么结论?
Rt△AB1C1∽Rt△AB2C2∽ Rt△AB3C3
验证猜想,形成概念
结论:在直角三角形中,对于每一个锐角A的值,不管三角形的大小如何,都有一个唯一的∠A的对边与邻边的比值和它对应
结论
A
B
C
∠A的对边
∠A的邻边
如图,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tanA ,即
当锐角A变化时,tanA的值也随之变化.
┌
问题6:回顾函数的概念,判断∠A的对边与邻边的比值是不是锐角A的函数
验证猜想,形成概念
注意
tanA是在直角三角形中定义的,∠A是一个锐
角(注意数形结合,构造直角三角形).
tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”号(注意tanA不表示tan乘以A).
tanA没有单位,它表示一个比值,即直角三角形中∠A的对边与邻边的比.
注意
tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
角相等,则正切值相等;两锐角的正切值相等,则这两个锐角相等.
A
C2
C1
B1
B2
梯子的倾斜程度与tanA有关系吗?
tanA的值越大,梯子越陡.
类比迁移,再探新知
展示与点拨
问题7:在Rt△ABC中,∠C=90°,类比正切函数的定义,判断∠A的对边与斜边的比值是不是锐角A的函数?∠A的邻边与斜边的比值呢?
A
B
C
∠A的对边
∠A的邻边
斜边
┌
在Rt△ABC中,如果锐角A确定,那么∠A的对边与斜边的比、邻边与斜边的比也随之确定.
A
B
C
∠A的对边
∠A的邻边
斜边
┌
概念归纳
∠A的对边与斜边的比叫做∠A的正弦,记作sinA,即
∠A的邻边与斜边的比叫做∠A的余弦,记作cosA,即
A
B
C
∠A的对边
∠A的邻边
斜边
┌
概念归纳
锐角A的正弦、余弦、正切,都是∠A的三角函数.
例1 下图表示两个自动扶梯,哪一个自动扶梯比较陡
5m
┌
13m
β
(乙)
(甲)
α
4m
┐
8m
解:甲梯中,
乙梯中,
∵tan α>tan β, ∴甲梯更陡.
理解概念,应用提升
检测与反馈
例2 如图,在Rt△ABC中,∠C=90 °,分别求两图中的sinA,
sinB.
理解概念,应用提升
A
C
B
3
4
A
B
C
5
13
1. 如图,△ABC是等腰三角形,你能根据图中所给数据求出tanC 吗?
B
C
A
1.5
4
D
理解概念,应用提升
拓展与延伸
2. 如图,Rt△ABC中,∠C=90 °, , AC=10,
AB等于多少?sinB呢?
A
B
C
理解概念,应用提升
拓展与延伸
3. 在等腰△ABC中,AB=AC=5,BC=6,求: sinA,cosA,tanA.
A
B
C
(1)什么是锐角的正切、正弦、余弦 如何求一个锐角的正切、正弦、余弦
(2)正切、正弦、余弦是函数吗 为什么
(3)在直角三角形中,一个锐角的正切、正弦、余弦值与三角形的边长是否有关系 只与什么有关系
(4)在直角三角形中,一个锐角的正切、正弦、余弦值随着这个锐角大小的改变分别有什么规律
(5)通过这节课的学习你掌握了哪些数学思想方法
回顾归纳,总结反思
达标测评,形成能力
(1)在RtΔABC中,锐角A的对边和斜边同时扩大100倍则sinA的值( )
A扩大100倍 B.缩小 C.不变 D.不能确定
(2)在RtΔABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,下列关系式正确的是( )
A. b=a.tanA B.b=c·sinA C.a=c.cosB D. c=a·sinA
(3)在RtΔABC中,∠C=90°,若AB=5,AC=4,则 sinA= .
(4)在RtΔABC中,∠C=90°,BC=2,sinA= ,则边AC= .
(5)在Rt△ABC中,∠C=90°,如果cosA= ,则tanB= .
锐角三角函数
第一课时
1.经历探索直角三角形中边角关系的过程,能说出正切的定义及表示方法,并类比说出正弦、余弦的定义及表示方法,并能够举例说明;
2.能够用 tanA.sinA.cosA表示直角三角形中两直角边的比,并能进行简单计算.
学习目标
整体感知,导入新课
我们在直角三角形中学过哪些关系?
一是直角三角形中边边之间的关系,也就是勾股定理.
二是角角之间的关系,就是直角三角形当中的两个锐角互余.
那么这一章我们将研究什么问题呢?
就是直角三角形中边和角之间的关系。那么在直角三角形中边和角有什么样的关系呢?
整体感知,导入新课
问题1:本节课研究直角三角形的边角关系,想研究边与角的关系,首先需要确定个角,再研究它与两边的关系,前面研究过任意两边的和、差关系,接下来研究比商关系;存在几种两边比商关系
自学与合作
根据特殊,引发猜想
问题2:在直角三角形中,45°角的对边与邻边的比值是多少 改变三角形的大小,这个结论还成立吗
自学与合作
问题3:把直角三角形中这个45°的角换成30°时,它的对边与邻边的比值还是一个固定值吗 改变三角形的大小,这个结论还成立吗 再换成60°呢
在RtΔABC,∠C=90°.
当∠A=45°时,∠A的对边与邻边的比值是固定值1;
当∠A=30°时,∠A的对边与邻边的比值是固定值 ;
当∠A=60°时,∠A的对边与邻边的比值是固定值 .
与三角形的大小无关.
根据特殊,引发猜想
自学与合作
问题4:根据上面的总结,在Rt△ABC中,∠C=90°,当∠A取其它一定度数的锐角时,它的对边与邻边的比值会出现什么情况 对此,你有怎样的猜想
猜想:在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,它的对边与邻边的比也是一个固定值.
验证猜想,形成概念
自学与合作
问题5:你的猜想正确吗 如果正确,请说明理由;如果不正确,请举出反例.
A
C2
C1
B1
B2
(1)Rt△AB1C1和Rt△AB2C2有什么关系
Rt△AB1C1∽Rt△AB2C2
(2)
A
C2
C1
B1
B2
B3
C3
(3)如果改变B2在梯子上的位置(如B3C3 )呢?由此你能得出什么结论?
Rt△AB1C1∽Rt△AB2C2∽ Rt△AB3C3
验证猜想,形成概念
结论:在直角三角形中,对于每一个锐角A的值,不管三角形的大小如何,都有一个唯一的∠A的对边与邻边的比值和它对应
结论
A
B
C
∠A的对边
∠A的邻边
如图,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tanA ,即
当锐角A变化时,tanA的值也随之变化.
┌
问题6:回顾函数的概念,判断∠A的对边与邻边的比值是不是锐角A的函数
验证猜想,形成概念
注意
tanA是在直角三角形中定义的,∠A是一个锐
角(注意数形结合,构造直角三角形).
tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”号(注意tanA不表示tan乘以A).
tanA没有单位,它表示一个比值,即直角三角形中∠A的对边与邻边的比.
注意
tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
角相等,则正切值相等;两锐角的正切值相等,则这两个锐角相等.
A
C2
C1
B1
B2
梯子的倾斜程度与tanA有关系吗?
tanA的值越大,梯子越陡.
类比迁移,再探新知
展示与点拨
问题7:在Rt△ABC中,∠C=90°,类比正切函数的定义,判断∠A的对边与斜边的比值是不是锐角A的函数?∠A的邻边与斜边的比值呢?
A
B
C
∠A的对边
∠A的邻边
斜边
┌
在Rt△ABC中,如果锐角A确定,那么∠A的对边与斜边的比、邻边与斜边的比也随之确定.
A
B
C
∠A的对边
∠A的邻边
斜边
┌
概念归纳
∠A的对边与斜边的比叫做∠A的正弦,记作sinA,即
∠A的邻边与斜边的比叫做∠A的余弦,记作cosA,即
A
B
C
∠A的对边
∠A的邻边
斜边
┌
概念归纳
锐角A的正弦、余弦、正切,都是∠A的三角函数.
例1 下图表示两个自动扶梯,哪一个自动扶梯比较陡
5m
┌
13m
β
(乙)
(甲)
α
4m
┐
8m
解:甲梯中,
乙梯中,
∵tan α>tan β, ∴甲梯更陡.
理解概念,应用提升
检测与反馈
例2 如图,在Rt△ABC中,∠C=90 °,分别求两图中的sinA,
sinB.
理解概念,应用提升
A
C
B
3
4
A
B
C
5
13
1. 如图,△ABC是等腰三角形,你能根据图中所给数据求出tanC 吗?
B
C
A
1.5
4
D
理解概念,应用提升
拓展与延伸
2. 如图,Rt△ABC中,∠C=90 °, , AC=10,
AB等于多少?sinB呢?
A
B
C
理解概念,应用提升
拓展与延伸
3. 在等腰△ABC中,AB=AC=5,BC=6,求: sinA,cosA,tanA.
A
B
C
(1)什么是锐角的正切、正弦、余弦 如何求一个锐角的正切、正弦、余弦
(2)正切、正弦、余弦是函数吗 为什么
(3)在直角三角形中,一个锐角的正切、正弦、余弦值与三角形的边长是否有关系 只与什么有关系
(4)在直角三角形中,一个锐角的正切、正弦、余弦值随着这个锐角大小的改变分别有什么规律
(5)通过这节课的学习你掌握了哪些数学思想方法
回顾归纳,总结反思
达标测评,形成能力
(1)在RtΔABC中,锐角A的对边和斜边同时扩大100倍则sinA的值( )
A扩大100倍 B.缩小 C.不变 D.不能确定
(2)在RtΔABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,下列关系式正确的是( )
A. b=a.tanA B.b=c·sinA C.a=c.cosB D. c=a·sinA
(3)在RtΔABC中,∠C=90°,若AB=5,AC=4,则 sinA= .
(4)在RtΔABC中,∠C=90°,BC=2,sinA= ,则边AC= .
(5)在Rt△ABC中,∠C=90°,如果cosA= ,则tanB= .
