28.3 课时3 同弧所对圆周角与圆内接四边形 课件 (共15张PPT) 2024-2025学年冀教版数学九年级上册
文档属性
| 名称 | 28.3 课时3 同弧所对圆周角与圆内接四边形 课件 (共15张PPT) 2024-2025学年冀教版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 525.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-21 23:03:54 | ||
图片预览






文档简介
(共15张PPT)
28.3圆心角和圆周角
第3课时 圆内接四边形
1.理解并掌握圆内接四边形的概念及性质并会运用.
(重点)
学习目标
问题1 什么是圆周角?
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
圆周角概念:顶点在圆上,并且两边都和圆相交的角叫圆周角.
●O
B
A
C
D
E
回顾旧知
问题2 什么是圆周角定理?
圆周角定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半.
O
●
A
B
C
●
O
A
B
C
●
O
A
B
C
即∠ABC = ∠AOC.
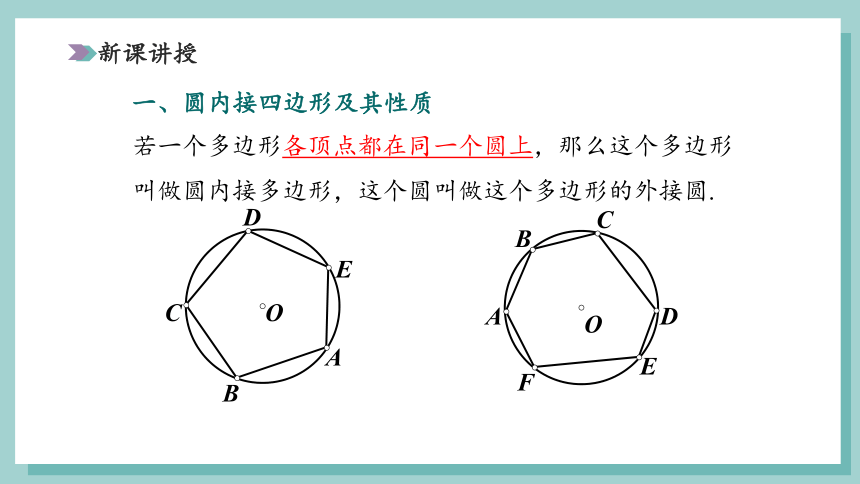
一、圆内接四边形及其性质
若一个多边形各顶点都在同一个圆上,那么这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
O
B
C
D
E
F
A
O
A
C
D
E
B
新课讲授
如图,四边形 ABCD 为☉O 的内接四边形,☉O 为四边形 ABCD 的外接圆.
(2)当四边形 ABCD 为一般四边形时,
猜想:∠A 与∠C,∠B 与∠D 之间的关系为 .
∠A +∠C = 180°,∠B +∠D = 180°
(1)当四边形 ABCD 为矩形时,∠A 与∠C,∠B 与∠D 之间的关系为 .
∠A +∠C = 180°,∠B +∠D = 180°
性质探究
证明:圆内接四边形的对角互补.
已知,如图四边形 ABCD 为☉O 的内接四边形,☉O 为四边形 ABCD 的外接圆. 求证:∠BAD +∠BCD = 180°.
证明:连接 OB、OD.
根据圆周角定理,可知
1
2
由四边形内角和定理可知,∠ABC +∠ADC = 180°.
证一证
圆内接四边形的对角互补.
性质
归纳总结
C
O
D
B
A
∵∠A+∠DCB=180°,
E
∠DCB+∠DCE=180°.
∴∠A=∠DCE.
如图,∠DCE 是圆内接四边形 ABCD 的一个外角,∠A 与∠DCE 的大小有何关系?
想一想
1.四边形 ABCD 是 ⊙O 的内接四边形,且∠A = 110°,∠B = 80°,则∠C = ,∠D = .
2.⊙O 的内接四边形 ABCD 中,
∠A∶∠B∶∠C = 1∶2∶3 ,则∠D = .
70°
100°
90°
练一练
3. 如图,在 ⊙O 的内接四边形 ABCD 中,∠BOD=120°,那么∠BCD 是( )
A.120° B.100°
C.80° D.60°
解析:∵∠BOD=120°,
∴∠A=60°,
∴∠C=180°-60°=120°,故选 A.
A
1.在⊙O 中,∠CBD = 30°,∠BDC = 20°,求∠A.
O
A
B
D
C
解:∵∠CBD = 30°,∠BDC = 20°,
∴∠C = 180° -∠CBD -∠BDC = 130°.
∴∠A = 180° -∠C = 50°.
(圆内接四边形对角互补)
当堂检测
解:延长 AO 与圆交于点 D,连接 BD, 则∠ABD = 90°.
∵∠OAB = 40°,
∴∠ADB = 50°.
∴∠C = 180° -∠ADB = 130°.
变式:已知∠OAB 等于 40°,求∠C 的度数.
A
B
C
O
D
2.判断.
(1)等弧所对的圆周角相等;( )
(2)相等的弦所对的圆周角也相等;( )
(3)90° 的角所对的弦是直径;( )
(4)同弦所对的圆周角相等.( )
×
×
×
×
2.圆内接四边形的性质定理:圆的内接四边形对角互补,且任何一个外角都等于它的内对角.
1.若一个四边形各顶点都在同一个圆上,则这个四边形叫做圆内接四边形,这个圆叫做这个四边形的外接圆.
课堂小结
28.3圆心角和圆周角
第3课时 圆内接四边形
1.理解并掌握圆内接四边形的概念及性质并会运用.
(重点)
学习目标
问题1 什么是圆周角?
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
圆周角概念:顶点在圆上,并且两边都和圆相交的角叫圆周角.
●O
B
A
C
D
E
回顾旧知
问题2 什么是圆周角定理?
圆周角定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半.
O
●
A
B
C
●
O
A
B
C
●
O
A
B
C
即∠ABC = ∠AOC.
一、圆内接四边形及其性质
若一个多边形各顶点都在同一个圆上,那么这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
O
B
C
D
E
F
A
O
A
C
D
E
B
新课讲授
如图,四边形 ABCD 为☉O 的内接四边形,☉O 为四边形 ABCD 的外接圆.
(2)当四边形 ABCD 为一般四边形时,
猜想:∠A 与∠C,∠B 与∠D 之间的关系为 .
∠A +∠C = 180°,∠B +∠D = 180°
(1)当四边形 ABCD 为矩形时,∠A 与∠C,∠B 与∠D 之间的关系为 .
∠A +∠C = 180°,∠B +∠D = 180°
性质探究
证明:圆内接四边形的对角互补.
已知,如图四边形 ABCD 为☉O 的内接四边形,☉O 为四边形 ABCD 的外接圆. 求证:∠BAD +∠BCD = 180°.
证明:连接 OB、OD.
根据圆周角定理,可知
1
2
由四边形内角和定理可知,∠ABC +∠ADC = 180°.
证一证
圆内接四边形的对角互补.
性质
归纳总结
C
O
D
B
A
∵∠A+∠DCB=180°,
E
∠DCB+∠DCE=180°.
∴∠A=∠DCE.
如图,∠DCE 是圆内接四边形 ABCD 的一个外角,∠A 与∠DCE 的大小有何关系?
想一想
1.四边形 ABCD 是 ⊙O 的内接四边形,且∠A = 110°,∠B = 80°,则∠C = ,∠D = .
2.⊙O 的内接四边形 ABCD 中,
∠A∶∠B∶∠C = 1∶2∶3 ,则∠D = .
70°
100°
90°
练一练
3. 如图,在 ⊙O 的内接四边形 ABCD 中,∠BOD=120°,那么∠BCD 是( )
A.120° B.100°
C.80° D.60°
解析:∵∠BOD=120°,
∴∠A=60°,
∴∠C=180°-60°=120°,故选 A.
A
1.在⊙O 中,∠CBD = 30°,∠BDC = 20°,求∠A.
O
A
B
D
C
解:∵∠CBD = 30°,∠BDC = 20°,
∴∠C = 180° -∠CBD -∠BDC = 130°.
∴∠A = 180° -∠C = 50°.
(圆内接四边形对角互补)
当堂检测
解:延长 AO 与圆交于点 D,连接 BD, 则∠ABD = 90°.
∵∠OAB = 40°,
∴∠ADB = 50°.
∴∠C = 180° -∠ADB = 130°.
变式:已知∠OAB 等于 40°,求∠C 的度数.
A
B
C
O
D
2.判断.
(1)等弧所对的圆周角相等;( )
(2)相等的弦所对的圆周角也相等;( )
(3)90° 的角所对的弦是直径;( )
(4)同弦所对的圆周角相等.( )
×
×
×
×
2.圆内接四边形的性质定理:圆的内接四边形对角互补,且任何一个外角都等于它的内对角.
1.若一个四边形各顶点都在同一个圆上,则这个四边形叫做圆内接四边形,这个圆叫做这个四边形的外接圆.
课堂小结
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
