苏科版八年级数学上册试题 第3章勾股定理 章节复习卷 (含解析)
文档属性
| 名称 | 苏科版八年级数学上册试题 第3章勾股定理 章节复习卷 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 510.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-22 16:16:19 | ||
图片预览



文档简介
第3章《勾股定理》章节复习卷
一.选择题(每小题2分,共12分)
1.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为
A.9 B.6 C.4 D.3
2..在中,,,的对边分别是,,,下列说法错误的是( )
A.若,则是直角三角形
B.若,则△是直角三角形
C.若,则是直角三角形
D.若,则不是直角三角形
3.如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B,C).若线段AD长为正整数,则点D的个数共有( )
A.5个 B.4个 C.3个 D.2个
4.如图,小明在广场上先向东走米,又向南走米,再向西走米,又向南走米,再向东走米,小明到达的终止点与原出发点的距离为( )米.
A.80 B.100 C.110 D.180
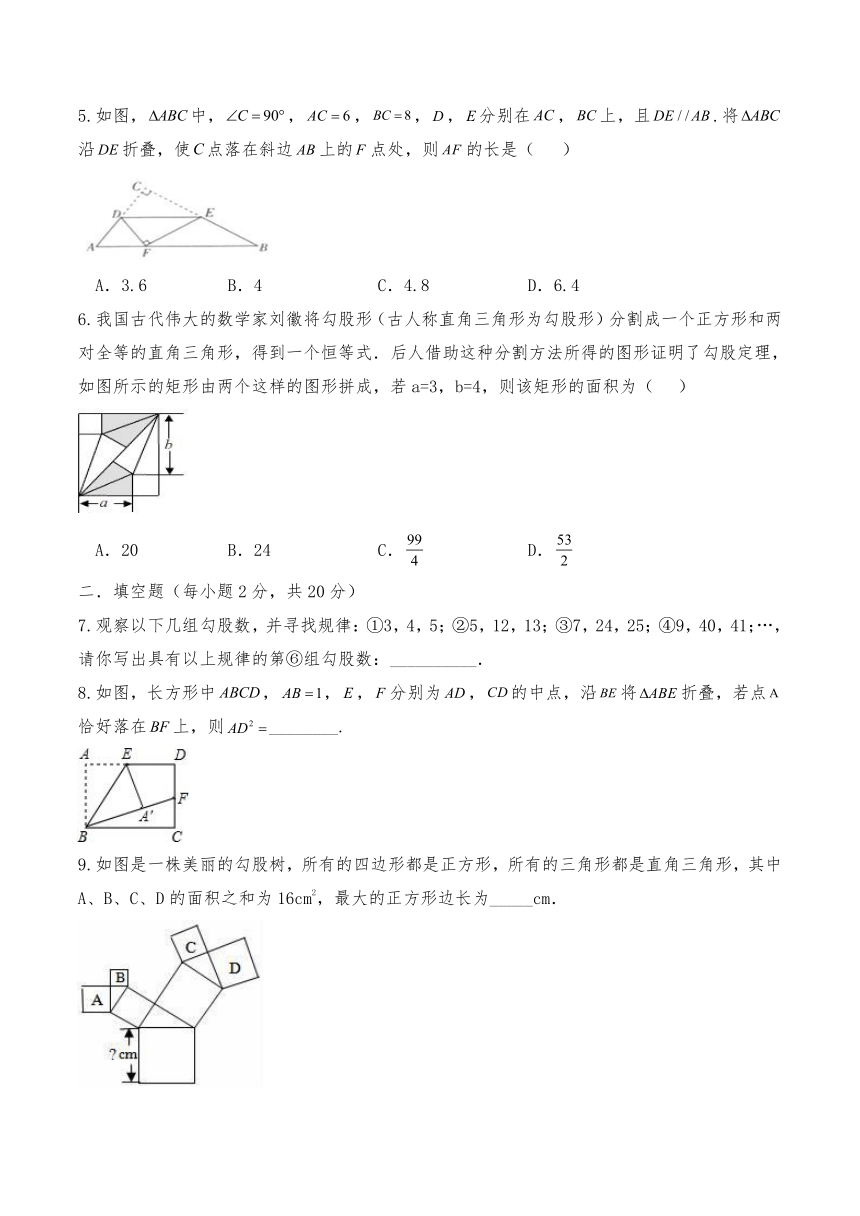
5.如图,中,,,,,分别在,上,且.将沿折叠,使点落在斜边上的点处,则的长是( )
A.3.6 B.4 C.4.8 D.6.4
6.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )
A.20 B.24 C. D.
二.填空题(每小题2分,共20分)
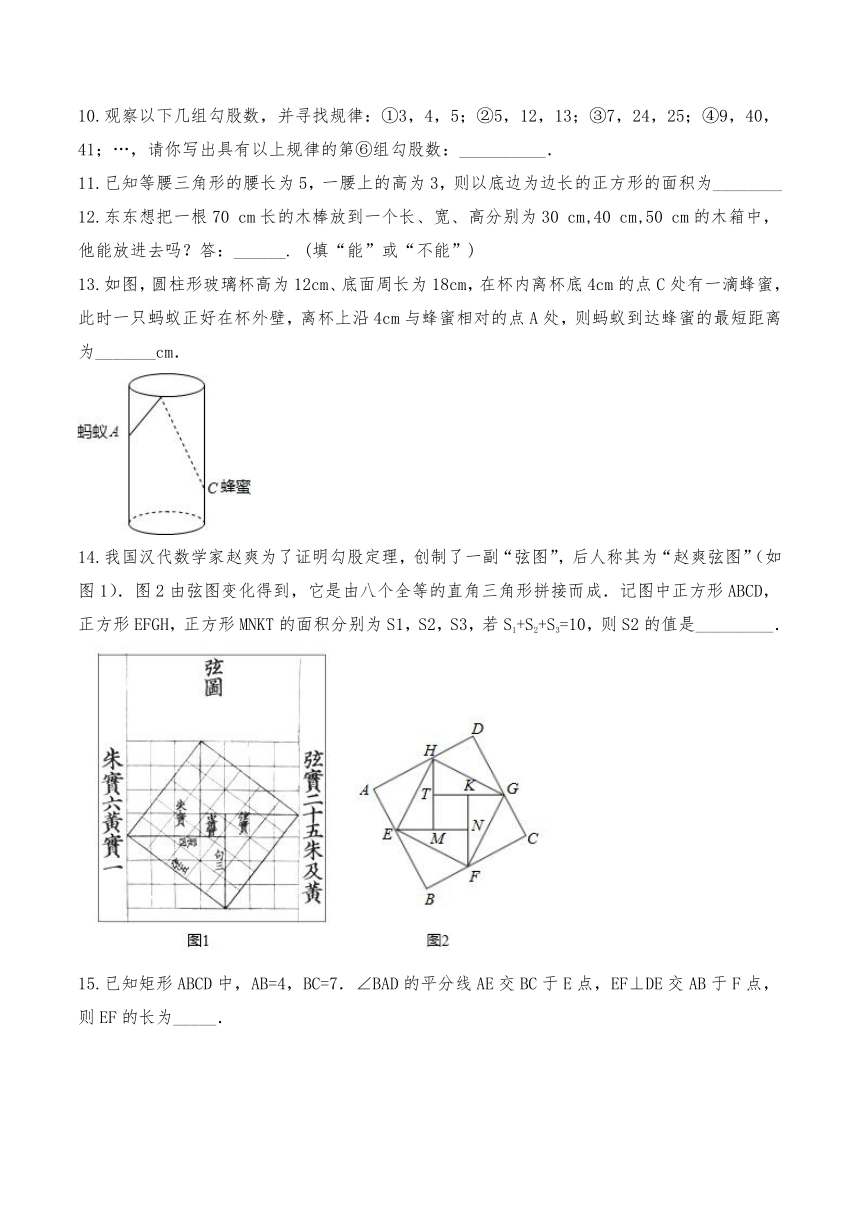
7.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…,请你写出具有以上规律的第⑥组勾股数:__________.
8.如图,长方形中,,,分别为,的中点,沿将折叠,若点恰好落在上,则________.
9.如图是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形,其中A、B、C、D的面积之和为16cm2,最大的正方形边长为_____cm.
10.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…,请你写出具有以上规律的第⑥组勾股数:__________.
11.已知等腰三角形的腰长为5,一腰上的高为3,则以底边为边长的正方形的面积为________
12.东东想把一根70 cm长的木棒放到一个长、宽、高分别为30 cm,40 cm,50 cm的木箱中,他能放进去吗?答:______. (填“能”或“不能”)
13.如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为_______cm.
14.我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=10,则S2的值是_________.
15.已知矩形ABCD中,AB=4,BC=7.∠BAD的平分线AE交BC于E点,EF⊥DE交AB于F点,则EF的长为_____.
16.如图,矩形中,,,将矩形绕点顺时针旋转得到矩形,边与交于点,延长交于点,若,则的长为______.
三.解答题
17.(10分)如图,一架云梯长米,斜靠在一面墙上,梯子靠墙的一端距地面米.
(1)这个梯子底端离墙有多少米?
(2)如果梯子的顶端下滑了米,那么梯子的底部在水平方向也滑动了米吗?
18.(8分)如图,在△ABC中,AB=AC=5,BC=6,M为BC的中点,MN⊥AC于点N,求MN的长.
19.(10分)《九章算术》中“勾股”一章有记载:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它的顶端恰好到达池边的水面,求芦苇的长度.(1丈=10尺)
解决下列问题:
(1)示意图中,线段AF的长为 尺,线段EF的长为 尺;
(2)求芦苇的长度.
20.(10分)如图第4号台风“黑格比”的中心于2020年8月5日下午位于浙江省绍兴市境内的B处,最大风力有9级(23m/s),中心最低气压为990百帕,台风中心沿东北(BC)方向以25km/h的速度向D移动在距离B地250km的正北方有一A地,已知A地到BC的距离AD=70km,那么台风中心经过多长时间从B点移到D点?如果在距台风中心70km的圆形区域内都将有受到台风破坏的危险,正在D点休闲的游人在接到台风警报后的几个小时内撤离才可脱离危险?
21.(10分)一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方法如图,火柴盒的一个侧面(是一个长方形)倒下到的位置连接,, ,设 ,,.
(1)试用,有关的代数式表示梯形的面积;
(2)试用,,有关的代数式分别表示,,的面积;
(3)由(1)和(2)的结论证明勾股定理:.
22.(10分)有一个如图所示的长方体的透明鱼缸,假设其长AD=80 cm,高AB=60 cm,水深AE=40 cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60 cm.一小虫想从鱼缸外的点A处沿缸壁爬到鱼缸内G处吃鱼饵.
(1)小虫应该走怎样的路线才可使爬行的路程最短?请画出它的爬行路线,并用箭头标注;
(2)试求小虫爬行的最短路程.
23.(10分)如图,已知△ABC中,∠B=90°,AB=8 cm,BC=6 cm,P,Q是△ABC边上的两个动点,点P从点A开始沿A→B方向运动,且速度为1 cm,点Q从点B开始沿B→C方向运动,且速度为2 cm/s,它们同时出发,设运动的时间为t s.
(1)运动几秒时,△APC是等腰三角形?
(2)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
答案
一.选择题
1.D
【解析】
故选D.
2..D
【解析】A项,,即,而,则,所以是直角三角形,说法正确;
B项,,即 ,所以是直角三角形,且,说法正确;
C项,,而,则,所以是直角三角形,说法正确;
D项,,,,,但是,所以可能是直角三角形,说法错误.
故选D.
3.C
【解析】过A作AE⊥BC于E,∵AB=AC=5,BC=8,∴BE=EC=4,∴AE=3,∵D是线段BC上的动点(不含端点B,C),∴AE≤AD<AB,即3≤AD<5,∵AD为正整数,∴AD=3或AD=4,当AD=4时,E的左右两边各有一个点D满足条件,∴点D的个数共有3个.故选C.
4.B
【解析】解答:解:连接AB,作AC⊥BC于C.
∵AC=40+40=80米,
BC=70-10=60米,
则AB==100米.
故选B.
5.A
【解析】解:如图,连接,
根据题意,得.因为,所以.因为,,,所以,所以,所以.所以,所以.
故选A.
6.B
【解析】设小正方形的边长为x,则矩形的一边长为(a+x),另一边为(b+x),根据题意得 :2(ax+x2+bx)=(a+x)(b+x),
化简得 :ax+x2+bx-ab=0,
又∵ a = 3 , b = 4 ,
∴x2+7x=12;
∴该矩形的面积为=(a+x)(b+x)=(3+x)(4+x)=x2+7x+12=24.
故答案为B.
二.填空题
7.13,84,85
【解析】由题意得,每组第一个数是奇数,且逐步递增2,第二、第三个数相差为一
故第⑥组的第一个数是13
设第二个数为x,第三个数为x+1
根据勾股定理得
解得
则第⑥组勾股数:13,84,85
故答案为:13,84,85.
8.2
【解析】连接EF,
∵点E、点F是AD、DC的中点,∴AE=ED,CF=DF=CD=AB=,
由折叠的性质可得AE=A′E,∴A′E=DE,
在Rt△EA′F和Rt△EDF中,
,
∴Rt△EA′F≌Rt△EDF(HL),∴A′F=DF=,
∴BF=BA′+A′F=AB+DF=1+=,
在Rt△BCF中,BC==.
∴AD=BC=.∴AD2=2
故答案是2.
9.4
【解析】由勾股定理得,A、B的面积之和等于E的面积,A、B、C、D的面积之和等于E、F的面积之和,
∴E、F的面积之和等于最大的正方形G的面积,
∴最大的正方形G的面积为A、B、C、D的面积之和=16cm2,
∴最大的正方形边长为4cm,
故答案为4.
10.13,84,85
【解析】由题意得,每组第一个数是奇数,且逐步递增2,第二、第三个数相差为一
故第⑥组的第一个数是13
设第二个数为x,第三个数为x+1
根据勾股定理得,解得
则第⑥组勾股数:13,84,85
故答案为:13,84,85.
11.10或90
【解析】根据题意作出图形分为高线在三角形内和高线在三角形外两种情况:
如图1,AC=5,CD=3,CD⊥AB,根据勾股定理可知:AD==4,
∴BD=1.∴BC2=12+32=10.
如图2,AC=5,CD=3,CD⊥AB,根据勾股定理可知:AD==4,
∴BD=9,∴BC2=92+32=90.
故答案是:10或90.
12.能
【解析】作如下长方体,其中AB=50cm,BC=40cm,CC′=30cm,连接AC、AC′,
在Rt△ABC中,AC2=AB2+BC2=4100,
在Rt△ACC′中,AC′=>70,故他能放进去.
故答案为能.
13.15.
【解析】沿过A的圆柱的高剪开,得出矩形EFGH,
过C作CQ⊥EF于Q,作A关于EH的对称点A′,连接A′C交EH于P,连接AP,则AP+PC就是蚂蚁到达蜂蜜的最短距离,
∵AE=A′E,A′P=AP,∴AP+PC=A′P+PC=A′C,
∵CQ=×18cm=9cm,A′Q=12cm-4cm+4cm=12cm,
在Rt△A′QC中,由勾股定理得:A′C==15cm,
故答案为15.
14..
【解析】将四边形MTKN的面积设为x,将其余八个全等的三角形面积一个设为y,
∵正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,S1+S2+S3=10,
∴得出S1=8y+x,S2=4y+x,S3=x,∴S1+S2+S3=3x+12y=10,故3x+12y=10,
x+4y=,所以S2=x+4y=.
15.5
【解析】连接DF,
在矩形ABCD中,∵AE平分∠BAD,
则在中,
在 中, 即 ①
在中, ②
在中, ③
化简可得 即
则在中,
故答案为:5.
16.
【解析】如图,连接,过点作,
设,则矩形中
在与中,
在中,
,故答案为:.
三.解答题
17.解:(1)由题意得此时a=24米,c=25米,根据a2+b2=c2,
∴b=7米;
(2)不是.设滑动后梯子的底端到墙的距离为b米,
得方程,b2+(24-4)2=252,
解得b=15,
所以梯子向后滑动了8米.
综合得:如果梯子的顶端下滑了4米,那么梯子的底部在水平方向不是滑4米.
18.解:连接AM,
∵AB=AC,M为BC的中点,∴AM⊥BC,CM=BC=3.
由勾股定理得AM 2=AC 2-CM 2=52-32=16,∴AM=4.
∵MN⊥AC,∴S△ACM=CM·AM=AC·MN,即3×4=5MN,
∴MN=2.4.
19.解:(1)由题意可得:EF=1尺,AF==5尺;
故答案为:5,1;
(2)设芦苇长EG=AG=x尺,则水深FG=(x-1)尺,
在Rt△AGF中,52+(x-1)2=x2,解得:x=13,
∴芦苇长13尺.
20.解:在ΔABD中,根据勾股定理,BD===240(km),
则台风中心经过240÷25=小时从B点移到D点,
如图,距台风中心70km的圆形区域内都会受到不同程度的影响,
∴所以人们要在台风中心到达E点之前撤离,
∵BE=BD -DE=240-70=170km,170÷25=(小时),
∴正在D点休闲的游人在接到台风警报后的小时内撤离才可脱离危险.
21.(1)由题意, 可得梯形的面积为
(2)由题意易知,,
所以,为直角三角形,
所以,
又因为,,
所以.
(3)由题中图形可知,
所以,
所以,
所以
22.(1)如图所示,AQ→QG为最短路线,
(2)因为AE=40cm,AA′=120cm,所以A′E=120-40=80(cm),
因为EG=60cm,所以A′G2=A′E2+EG2=802+602=10000,
所以A′G=100cm,所以AQ+QG=A′Q+QG=A′G=100cm,
所以小虫爬行的最短路程为100cm.
23.(1)由题意可知AP=t,PC=
∵AP=PC,
∴t=,
解得,t=,
∴出发秒后△APC能形成等腰三角形;
(2)在△ABC中,由勾股定理可求得AC=10,
当点Q在AC上时,AQ=BC+AC-2t=16-2t,所以CQ=AC-AQ=10-(16-2t)=2t-6,
当BQ=BC=6时,如图1,过B作BD⊥AC,则CD=CQ=t-3,在Rt△ABC中,可求得BD=,
在Rt△BCD中,由勾股定理可得BC2=BD2+CD2,即62=()2+(t-3)2,
解得t=或t=-<0(舍去);
当CQ=BC=6时,则2t-6=6,解得t=6,
当CQ=BQ时,则∠C=∠QBC,
∴∠C+∠A=∠CBQ+∠QBA,∴∠A=∠QBA,∴QB=QA,
∴CQ=AC=5,即2t-6=5,解得t=5.5,
综上可知当△BCQ为等腰三角形时,t=或t=6或t=5.5.
一.选择题(每小题2分,共12分)
1.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为
A.9 B.6 C.4 D.3
2..在中,,,的对边分别是,,,下列说法错误的是( )
A.若,则是直角三角形
B.若,则△是直角三角形
C.若,则是直角三角形
D.若,则不是直角三角形
3.如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B,C).若线段AD长为正整数,则点D的个数共有( )
A.5个 B.4个 C.3个 D.2个
4.如图,小明在广场上先向东走米,又向南走米,再向西走米,又向南走米,再向东走米,小明到达的终止点与原出发点的距离为( )米.
A.80 B.100 C.110 D.180
5.如图,中,,,,,分别在,上,且.将沿折叠,使点落在斜边上的点处,则的长是( )
A.3.6 B.4 C.4.8 D.6.4
6.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )
A.20 B.24 C. D.
二.填空题(每小题2分,共20分)
7.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…,请你写出具有以上规律的第⑥组勾股数:__________.
8.如图,长方形中,,,分别为,的中点,沿将折叠,若点恰好落在上,则________.
9.如图是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形,其中A、B、C、D的面积之和为16cm2,最大的正方形边长为_____cm.
10.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…,请你写出具有以上规律的第⑥组勾股数:__________.
11.已知等腰三角形的腰长为5,一腰上的高为3,则以底边为边长的正方形的面积为________
12.东东想把一根70 cm长的木棒放到一个长、宽、高分别为30 cm,40 cm,50 cm的木箱中,他能放进去吗?答:______. (填“能”或“不能”)
13.如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为_______cm.
14.我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=10,则S2的值是_________.
15.已知矩形ABCD中,AB=4,BC=7.∠BAD的平分线AE交BC于E点,EF⊥DE交AB于F点,则EF的长为_____.
16.如图,矩形中,,,将矩形绕点顺时针旋转得到矩形,边与交于点,延长交于点,若,则的长为______.
三.解答题
17.(10分)如图,一架云梯长米,斜靠在一面墙上,梯子靠墙的一端距地面米.
(1)这个梯子底端离墙有多少米?
(2)如果梯子的顶端下滑了米,那么梯子的底部在水平方向也滑动了米吗?
18.(8分)如图,在△ABC中,AB=AC=5,BC=6,M为BC的中点,MN⊥AC于点N,求MN的长.
19.(10分)《九章算术》中“勾股”一章有记载:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它的顶端恰好到达池边的水面,求芦苇的长度.(1丈=10尺)
解决下列问题:
(1)示意图中,线段AF的长为 尺,线段EF的长为 尺;
(2)求芦苇的长度.
20.(10分)如图第4号台风“黑格比”的中心于2020年8月5日下午位于浙江省绍兴市境内的B处,最大风力有9级(23m/s),中心最低气压为990百帕,台风中心沿东北(BC)方向以25km/h的速度向D移动在距离B地250km的正北方有一A地,已知A地到BC的距离AD=70km,那么台风中心经过多长时间从B点移到D点?如果在距台风中心70km的圆形区域内都将有受到台风破坏的危险,正在D点休闲的游人在接到台风警报后的几个小时内撤离才可脱离危险?
21.(10分)一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方法如图,火柴盒的一个侧面(是一个长方形)倒下到的位置连接,, ,设 ,,.
(1)试用,有关的代数式表示梯形的面积;
(2)试用,,有关的代数式分别表示,,的面积;
(3)由(1)和(2)的结论证明勾股定理:.
22.(10分)有一个如图所示的长方体的透明鱼缸,假设其长AD=80 cm,高AB=60 cm,水深AE=40 cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60 cm.一小虫想从鱼缸外的点A处沿缸壁爬到鱼缸内G处吃鱼饵.
(1)小虫应该走怎样的路线才可使爬行的路程最短?请画出它的爬行路线,并用箭头标注;
(2)试求小虫爬行的最短路程.
23.(10分)如图,已知△ABC中,∠B=90°,AB=8 cm,BC=6 cm,P,Q是△ABC边上的两个动点,点P从点A开始沿A→B方向运动,且速度为1 cm,点Q从点B开始沿B→C方向运动,且速度为2 cm/s,它们同时出发,设运动的时间为t s.
(1)运动几秒时,△APC是等腰三角形?
(2)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
答案
一.选择题
1.D
【解析】
故选D.
2..D
【解析】A项,,即,而,则,所以是直角三角形,说法正确;
B项,,即 ,所以是直角三角形,且,说法正确;
C项,,而,则,所以是直角三角形,说法正确;
D项,,,,,但是,所以可能是直角三角形,说法错误.
故选D.
3.C
【解析】过A作AE⊥BC于E,∵AB=AC=5,BC=8,∴BE=EC=4,∴AE=3,∵D是线段BC上的动点(不含端点B,C),∴AE≤AD<AB,即3≤AD<5,∵AD为正整数,∴AD=3或AD=4,当AD=4时,E的左右两边各有一个点D满足条件,∴点D的个数共有3个.故选C.
4.B
【解析】解答:解:连接AB,作AC⊥BC于C.
∵AC=40+40=80米,
BC=70-10=60米,
则AB==100米.
故选B.
5.A
【解析】解:如图,连接,
根据题意,得.因为,所以.因为,,,所以,所以,所以.所以,所以.
故选A.
6.B
【解析】设小正方形的边长为x,则矩形的一边长为(a+x),另一边为(b+x),根据题意得 :2(ax+x2+bx)=(a+x)(b+x),
化简得 :ax+x2+bx-ab=0,
又∵ a = 3 , b = 4 ,
∴x2+7x=12;
∴该矩形的面积为=(a+x)(b+x)=(3+x)(4+x)=x2+7x+12=24.
故答案为B.
二.填空题
7.13,84,85
【解析】由题意得,每组第一个数是奇数,且逐步递增2,第二、第三个数相差为一
故第⑥组的第一个数是13
设第二个数为x,第三个数为x+1
根据勾股定理得
解得
则第⑥组勾股数:13,84,85
故答案为:13,84,85.
8.2
【解析】连接EF,
∵点E、点F是AD、DC的中点,∴AE=ED,CF=DF=CD=AB=,
由折叠的性质可得AE=A′E,∴A′E=DE,
在Rt△EA′F和Rt△EDF中,
,
∴Rt△EA′F≌Rt△EDF(HL),∴A′F=DF=,
∴BF=BA′+A′F=AB+DF=1+=,
在Rt△BCF中,BC==.
∴AD=BC=.∴AD2=2
故答案是2.
9.4
【解析】由勾股定理得,A、B的面积之和等于E的面积,A、B、C、D的面积之和等于E、F的面积之和,
∴E、F的面积之和等于最大的正方形G的面积,
∴最大的正方形G的面积为A、B、C、D的面积之和=16cm2,
∴最大的正方形边长为4cm,
故答案为4.
10.13,84,85
【解析】由题意得,每组第一个数是奇数,且逐步递增2,第二、第三个数相差为一
故第⑥组的第一个数是13
设第二个数为x,第三个数为x+1
根据勾股定理得,解得
则第⑥组勾股数:13,84,85
故答案为:13,84,85.
11.10或90
【解析】根据题意作出图形分为高线在三角形内和高线在三角形外两种情况:
如图1,AC=5,CD=3,CD⊥AB,根据勾股定理可知:AD==4,
∴BD=1.∴BC2=12+32=10.
如图2,AC=5,CD=3,CD⊥AB,根据勾股定理可知:AD==4,
∴BD=9,∴BC2=92+32=90.
故答案是:10或90.
12.能
【解析】作如下长方体,其中AB=50cm,BC=40cm,CC′=30cm,连接AC、AC′,
在Rt△ABC中,AC2=AB2+BC2=4100,
在Rt△ACC′中,AC′=>70,故他能放进去.
故答案为能.
13.15.
【解析】沿过A的圆柱的高剪开,得出矩形EFGH,
过C作CQ⊥EF于Q,作A关于EH的对称点A′,连接A′C交EH于P,连接AP,则AP+PC就是蚂蚁到达蜂蜜的最短距离,
∵AE=A′E,A′P=AP,∴AP+PC=A′P+PC=A′C,
∵CQ=×18cm=9cm,A′Q=12cm-4cm+4cm=12cm,
在Rt△A′QC中,由勾股定理得:A′C==15cm,
故答案为15.
14..
【解析】将四边形MTKN的面积设为x,将其余八个全等的三角形面积一个设为y,
∵正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,S1+S2+S3=10,
∴得出S1=8y+x,S2=4y+x,S3=x,∴S1+S2+S3=3x+12y=10,故3x+12y=10,
x+4y=,所以S2=x+4y=.
15.5
【解析】连接DF,
在矩形ABCD中,∵AE平分∠BAD,
则在中,
在 中, 即 ①
在中, ②
在中, ③
化简可得 即
则在中,
故答案为:5.
16.
【解析】如图,连接,过点作,
设,则矩形中
在与中,
在中,
,故答案为:.
三.解答题
17.解:(1)由题意得此时a=24米,c=25米,根据a2+b2=c2,
∴b=7米;
(2)不是.设滑动后梯子的底端到墙的距离为b米,
得方程,b2+(24-4)2=252,
解得b=15,
所以梯子向后滑动了8米.
综合得:如果梯子的顶端下滑了4米,那么梯子的底部在水平方向不是滑4米.
18.解:连接AM,
∵AB=AC,M为BC的中点,∴AM⊥BC,CM=BC=3.
由勾股定理得AM 2=AC 2-CM 2=52-32=16,∴AM=4.
∵MN⊥AC,∴S△ACM=CM·AM=AC·MN,即3×4=5MN,
∴MN=2.4.
19.解:(1)由题意可得:EF=1尺,AF==5尺;
故答案为:5,1;
(2)设芦苇长EG=AG=x尺,则水深FG=(x-1)尺,
在Rt△AGF中,52+(x-1)2=x2,解得:x=13,
∴芦苇长13尺.
20.解:在ΔABD中,根据勾股定理,BD===240(km),
则台风中心经过240÷25=小时从B点移到D点,
如图,距台风中心70km的圆形区域内都会受到不同程度的影响,
∴所以人们要在台风中心到达E点之前撤离,
∵BE=BD -DE=240-70=170km,170÷25=(小时),
∴正在D点休闲的游人在接到台风警报后的小时内撤离才可脱离危险.
21.(1)由题意, 可得梯形的面积为
(2)由题意易知,,
所以,为直角三角形,
所以,
又因为,,
所以.
(3)由题中图形可知,
所以,
所以,
所以
22.(1)如图所示,AQ→QG为最短路线,
(2)因为AE=40cm,AA′=120cm,所以A′E=120-40=80(cm),
因为EG=60cm,所以A′G2=A′E2+EG2=802+602=10000,
所以A′G=100cm,所以AQ+QG=A′Q+QG=A′G=100cm,
所以小虫爬行的最短路程为100cm.
23.(1)由题意可知AP=t,PC=
∵AP=PC,
∴t=,
解得,t=,
∴出发秒后△APC能形成等腰三角形;
(2)在△ABC中,由勾股定理可求得AC=10,
当点Q在AC上时,AQ=BC+AC-2t=16-2t,所以CQ=AC-AQ=10-(16-2t)=2t-6,
当BQ=BC=6时,如图1,过B作BD⊥AC,则CD=CQ=t-3,在Rt△ABC中,可求得BD=,
在Rt△BCD中,由勾股定理可得BC2=BD2+CD2,即62=()2+(t-3)2,
解得t=或t=-<0(舍去);
当CQ=BC=6时,则2t-6=6,解得t=6,
当CQ=BQ时,则∠C=∠QBC,
∴∠C+∠A=∠CBQ+∠QBA,∴∠A=∠QBA,∴QB=QA,
∴CQ=AC=5,即2t-6=5,解得t=5.5,
综上可知当△BCQ为等腰三角形时,t=或t=6或t=5.5.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
