1.4线段、角的轴对称性课时训练

本资料来自于资源最齐全的２１世纪教育网www.21cnjy.com
1.4 线段、角的轴对称性
[趣题导学]
如图1.4-1，初二（1）班与初二（2）班这两个班的学生分别在M、N两处参加劳动，现要在道路AB、AC的交叉区域内设一个茶水供应点P，使P到两条道路的距离相等，且使PM=PN，你能找出符合条件的点P，并简要说明理由吗？
图1.4-1 图1.4-2
解答：P点如图1.4-2所示，作∠BAC的角平分线AD，作线段MN的垂直平分线EF，AD与EF交于点P，因为AD平分∠BAC，所以点P到两条道路AB、AC的距离相等，又因为点P在线段MN的中垂线上，所以PM=PN。
[双基锤炼]
一、选择题
1、下列图形中，不是轴对称图形的是 （ ）
A. 两条相交直线 B. 线段
C.有公共端点的两条相等线段 D.有公共端点的两条不相等线段
2、到三角形的三个顶点距离相等的点是（ ）
A.三条角平分线的交点 B.三条中线的交点
C.三条高的交点 D.三条边的垂直平分线的交点
3、有下列图形：（1）两个点；（2）一条线段；（3）一个角；（4）一个长方形；（5）两条相交直线；（6）两条平行线。其中轴对称图形共有（ ）
A、3个 B、4个 C、5个 D、6个
4、已知：在△ABC中，AD为∠BAC的角平分线上，DE⊥AB，F为AC上一点，且∠DFA=1000，则 （ ）
A.DE>DF B.DE二、填空题
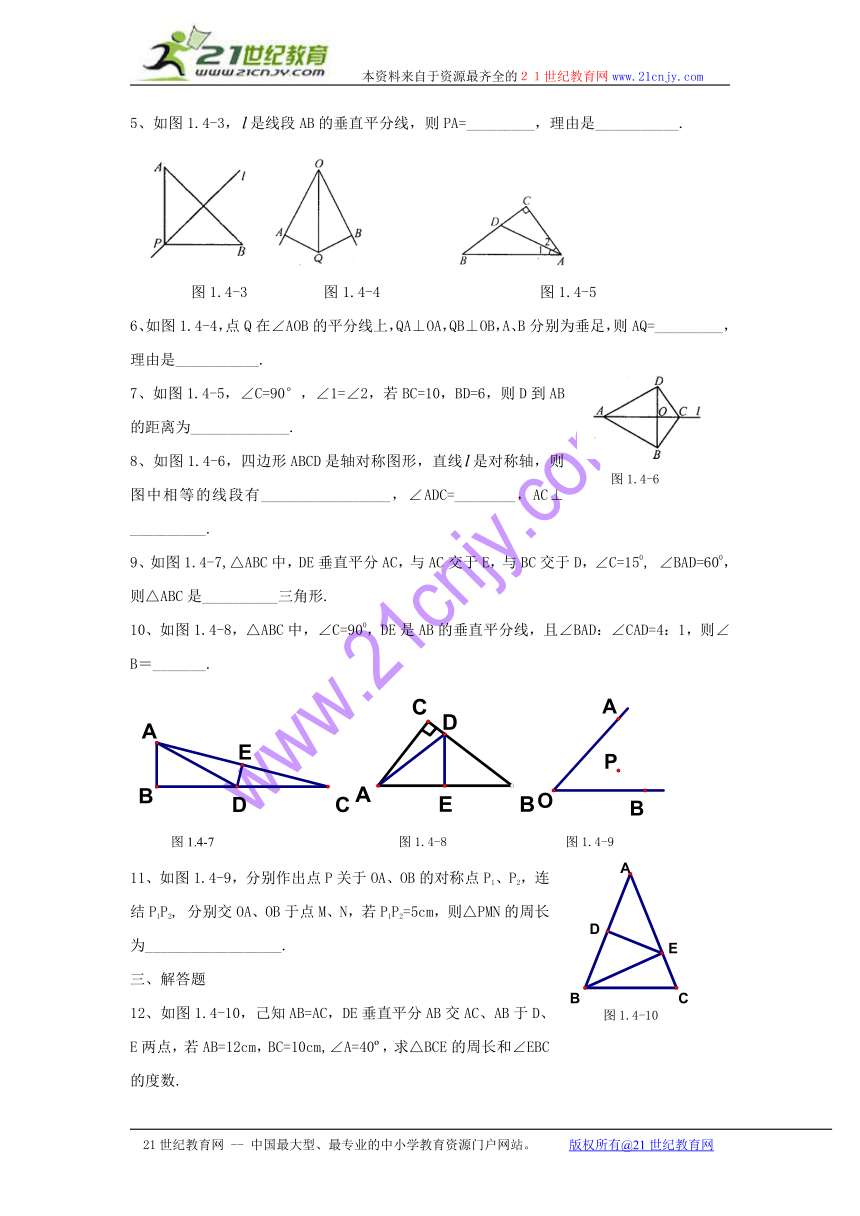
5、如图1.4-3，是线段AB的垂直平分线，则PA=_________，理由是___________.
图1.4-3 图1.4-4 图1.4-5
6、如图1.4-4，点Q在∠AOB的平分线上，QA⊥OA，QB⊥OB，A、B分别为垂足，则AQ=_________，理由是___________.
7、如图1.4-5，∠C=90°，∠1=∠2，若BC=10，BD=6，则D到AB的距离为_____________.
8、如图1.4-6，四边形ABCD是轴对称图形，直线是对称轴，则图中相等的线段有_________________，∠ADC=________，AC⊥__________.
9、如图1.4-7,△ABC中，DE垂直平分AC，与AC交于E，与BC交于D，∠C=150, ∠BAD=600，则△ABC是__________三角形.
10、如图1.4-8，△ABC中，∠C=900，DE是AB的垂直平分线，且∠BAD：∠CAD=4：1，则∠B＝_______.
11、如图1.4-9，分别作出点P关于OA、OB的对称点P1、P2，连结P1P2, 分别交OA、OB于点M、N，若P1P2=5cm，则△PMN的周长为__________________.
三、解答题
12、如图1.4-10，己知AB=AC，DE垂直平分AB交AC、AB于D、E两点，若AB=12cm，BC=10cm,∠A=40 ，求△BCE的周长和∠EBC的度数.
（以下空6行）
13、在Rt△ABC中，∠C=900，BD平分∠ABC交AC于点D，DE垂直平分线段AB，
（1） 试找出图中相等的线段，并说明理由。
（2） 若DE=1cm，BD=2cm，求AC的长。
( http: / / www.1230.org )
图1.4-11
[能力提升]
一、综合渗透
1、如图1.4-12，P是∠AOB的平分线上的一个点，PC⊥AO于C，PD⊥OB于D，写出图中一组相等的线段________（只需写出一组即可）.
2、如图1.4-13，在ΔABC中，BC=5 cm，BP、CP分别是∠ABC和∠ACB的角平分线，且PD∥AB，PE∥AC，则ΔPDE的周长是___________ cm.
3、已知: ∠AOB,点M、N.
求作：点P,使点P在∠AOB的平分线上,且PM=PN.
（要求：用尺规作图,保留作图痕迹,不写作法）
图1.4-14
二、应用创新
1、如图1.4-15，直线MN表示一条小河的河边，一牧民在点A处放马，现在要到河边去饮水，然后回到帐篷点B处（A、B在小河同旁）。问饮水地在何处时，才能使他们所走的路最短？在图中作出表示饮水处的点。
2、（1）如图1.4-16（1），作△ABC的两内角∠A、∠B的角平分线，设交点为O，点O在∠C的角平分线上吗？试说明你的猜想。你又有什么新的发现？
（2）如图1.4-16（2）作△ABC的两内角∠A、∠B的外角平分线，设交点为O，点O在∠C的角平分线上吗？试说明你的猜想。你又有什么新的发现？
（3）你能用你的发现解决下面的实际问题：如图1.4-16（3）直线L1、L2、L3表示三条互相交叉的公路，现要建一个加油站，要使它到三条公路的距离相等，画出符合要求的点的位置，共有几个？
（以下空6行）
3、（1）作△ABC的两边AB、BC的垂直平分线，设交点为O，点O在线段AC的垂直平分线
上吗？试说明你的猜想。你有什么新的发现？你能用你的发现解决下面的实际问题吗？
（2）现有三个村庄甲、乙、丙，现要新建一个水泵站P，使它到三个村庄的距离相等，应建在何处？（画出点P的位置）
图1.4-16
三、探究发散
1、已知:如图1.4-17,CDEF是一个矩形的台球面，有黑白两球分别位于点A、B两点，试问怎样撞击黑球A，使A先碰到台边EF反弹后再击中白球B？
（以下空3行）
2、有一个触壁游戏。规则如下：球从P点出发，先触OA壁，反弹后再触壁，再次反弹，┅┅若（至少经过两次）反弹，球能返回P点，则胜利。若你来玩这个游戏，假设速度不受其它限制，也不受其他因素干扰，你如何选择第一次的触壁点呢？
图1.4-18
3、如图1.4-19，已知P为∠AOB内任意一点，分别在OA、OB上，求作点P1、P2,使△PP1P2的周长最小。
4、如图1.4-20，AD∥BC，DC⊥AD，AE平分∠BAD，且E是的DC的中点，问AD，BC与AB之间有何关系？
[链接中考]
1、如图1.4-21，有A、B、C三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在( ).
A．在AC、BC两边高线的交点处
B．在AC、BC两边中线的交点处
C．在AC、BC两边垂直平分线的交点处
D．在∠A、∠B两内角平分线的交点处
2、（2005盐城）如图1.4-22，OP平分∠AOB，PC⊥OA于C，PD⊥OB于D，则PC与PD的大小关系（）　　　A．PC＞PD　　B．PC＝PD　　C．PC＜PD　　D．不能确定
图1.4-22
1.4 线段、角的轴对称性
[双基锤炼]
一、选择题
1、D 2、D 3、D 4、B
二、填空题
5、PB，线段垂直平分线上的点，到线段两端点的距离相等
6、BQ，角平分线上的点到角的两边的距离相等 7、4 8、AD=AB,DC=BC ,DO=OB，∠ABC，BD
9、直角 10、40°11、5cm
三、解答题
12、△BCE的周长为22cm，∠EBC=30°.
13、（1）AD=BD（线段垂直平分线上的点到线段两端点的距离相等）.
DC=DE（角平分线上的点到角的两边的距离相等）
（2）AC=3cm.
[能力提升]
一、综合渗透
1、PD=PC 或OD=OC 2、5
3、画出∠AOB的平分线,画出线段MN的垂直平分线,两直线的交点就是所求作的点P。
SHAPE \* MERGEFORMAT
二、应用创新
1、如图，点F为饮水点，此时BF+AF最短。
2、（1）点O在∠C的角平分线上。由此可以得到三角形的三条内角平分线相交于一点，这点到三条边的距离相等；
（2）点O在∠C的角平分线上。由此可以得到点O到三条边的距离相等；
（3）符合条件的点有4个：点G、H、I、J。
第2题图
3、（1）点O在线段AC的垂直平分线上。三角形的三条边的垂直平分线相交于一点，该点到三角形的三个顶点的距离相等。
（2）点P的位置如图所示。
第3题图
三、探究发散
1、如图，作出点A关于EF的对称点M，连结BM交EF于点N，则沿AN的方向撞击黑球A，可使A先碰到台边EF反弹后再击中白球B。
2、如图所示，分别作点P关于OA、OB的对称点P′、P′′，连结P′P′′，交OA于点E，则点E为第一次的触壁点。
3、如图所示，分别作点P关于OA、OB的对称点P′、P′′，连结P′P′′，交OA于点P1，交OB于点P2，则点P1、P2为所要求作的点。
( http: / / www.1230.org )
第2题图 第3题图
4、AD+BC=AB
[链接中考]
1、D 2、B
图1.4-6
图1.4-10
图1.4-7
图1.4-8
图1.4-9
图1.4-12
图4
图1.4-13
B．
A．
M
N
图1.4-15
（1） （2） （3）
图1.4-16
. P
O
A
B
图1.4-19
图1.4-20
A
B
C
图4
图1.4-21
第4题图
第3题图
第1题图
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网