11.2.2三角形的外角 课件(共26张PPT)
文档属性
| 名称 | 11.2.2三角形的外角 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-22 15:14:57 | ||
图片预览


文档简介
(共26张PPT)
人教版 八年级数学上
11.2.2 三角形的外角
学习目标
1.掌握三角形的外角的概念并能在能够复杂图形中找出外角.(难点)
3.掌握三角形的外角的性质,并利用其解决有关计算、推理问题(重、难点).
温故知新
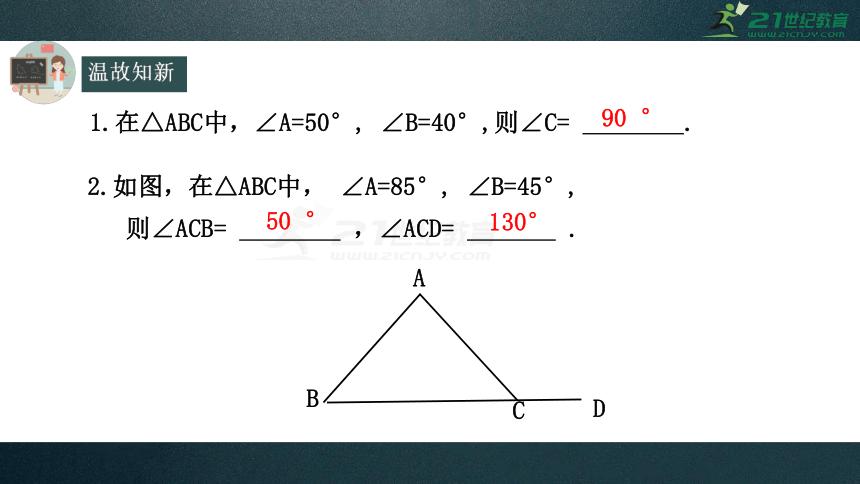
1.在△ABC中,∠A=50°, ∠B=40°,则∠C= .
90 °
2.如图,在△ABC中, ∠A=85°, ∠B=45°,
则∠ACB= ,∠ACD= .
A
B
C
D
50 °
130°
合作探究---三角形的外角的概念
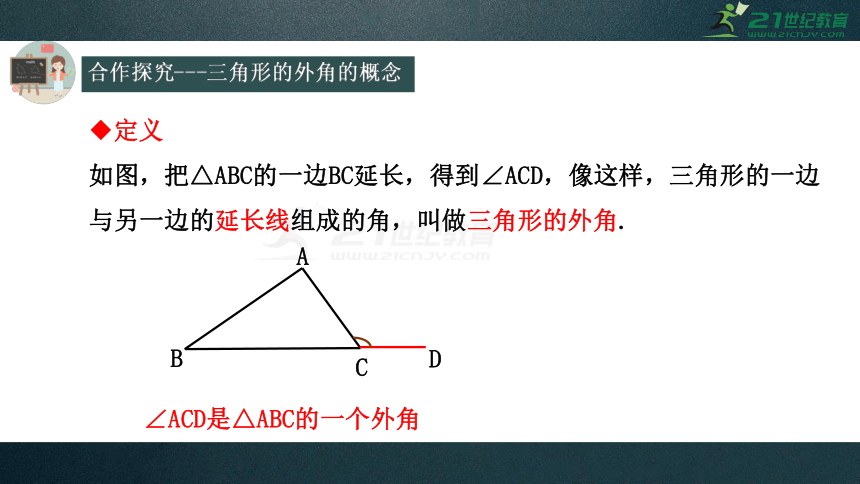
定义
如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
∠ACD是△ABC的一个外角
C
B
A
D
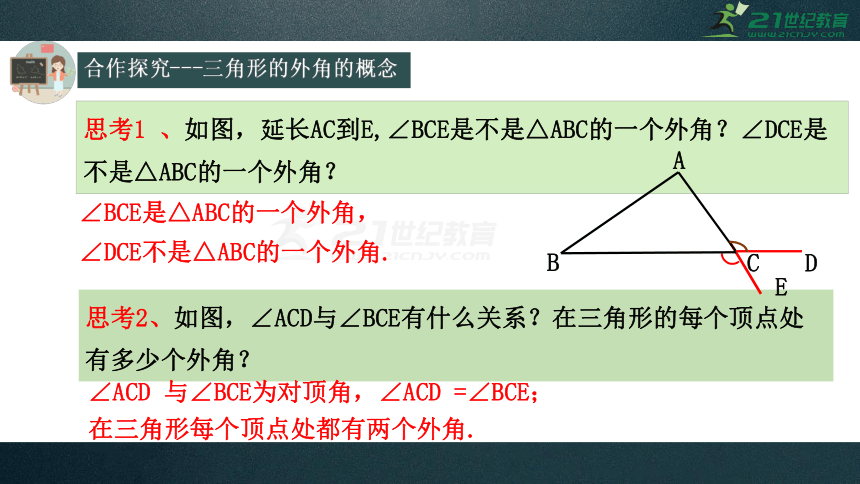
思考2、如图,∠ACD与∠BCE有什么关系?在三角形的每个顶点处有多少个外角?
思考1 、如图,延长AC到E,∠BCE是不是△ABC的一个外角?∠DCE是不是△ABC的一个外角?
E
在三角形每个顶点处都有两个外角.
∠ACD 与∠BCE为对顶角,∠ACD =∠BCE;
C
B
A
D
∠BCE是△ABC的一个外角,∠DCE不是△ABC的一个外角.
合作探究---三角形的外角的概念
合作探究---三角形的外角的概念
A
B
C
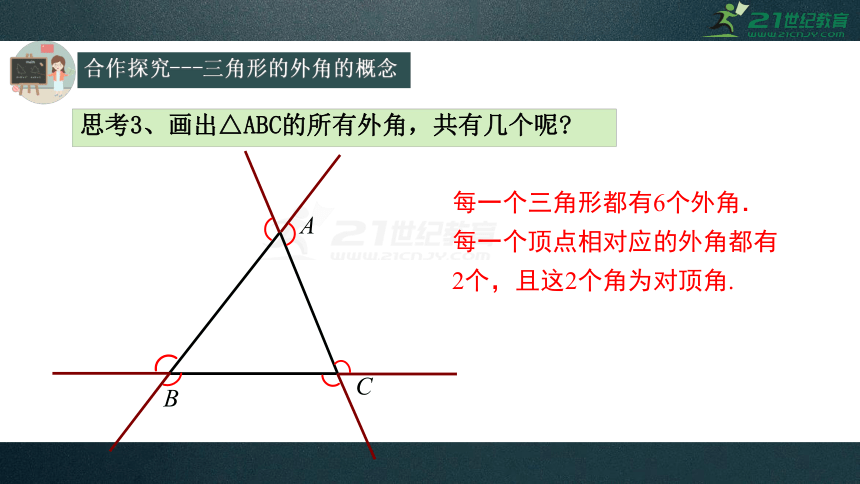
思考3、画出△ABC的所有外角,共有几个呢
每一个三角形都有6个外角.
每一个顶点相对应的外角都有
2个,且这2个角为对顶角.
小试牛刀
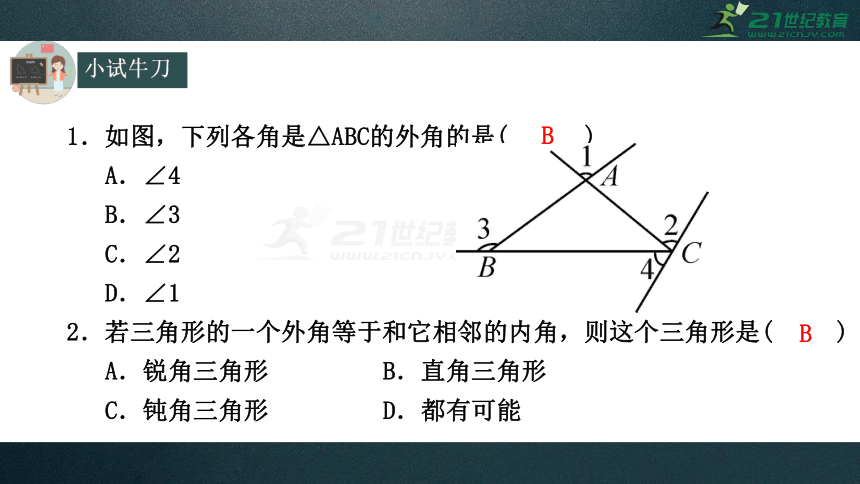
1.如图,下列各角是△ABC的外角的是( )
A.∠4
B.∠3
C.∠2
D.∠1
2.若三角形的一个外角等于和它相邻的内角,则这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.都有可能
B
B
小试牛刀
F
A
B
C
D
E
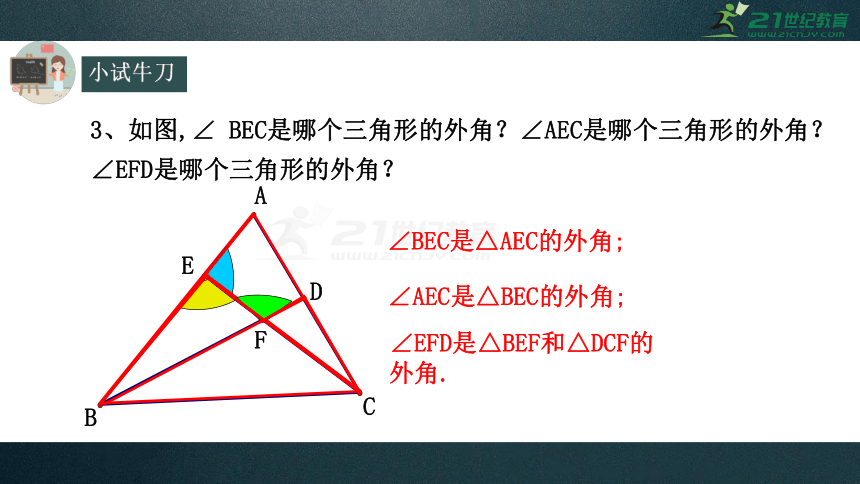
3、如图,∠ BEC是哪个三角形的外角?∠AEC是哪个三角形的外角?∠EFD是哪个三角形的外角?
∠BEC是△AEC的外角;
∠AEC是△BEC的外角;
∠EFD是△BEF和△DCF的外角.
合作探究---三角形的外角的性质
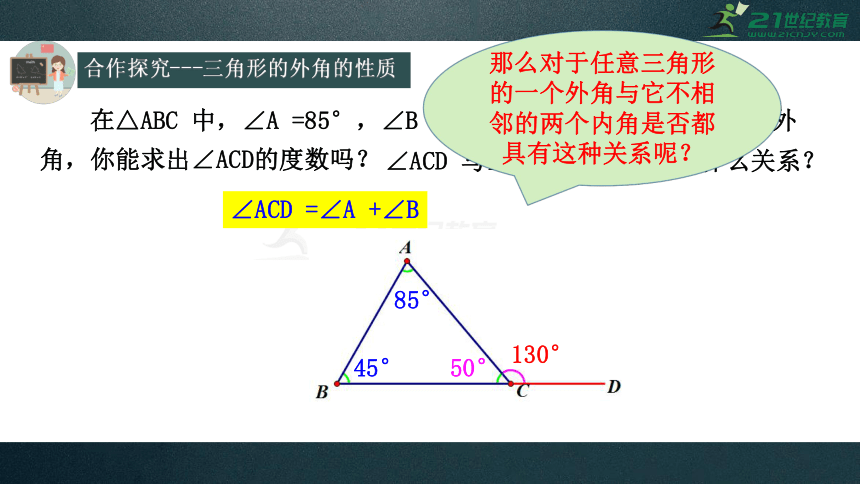
在△ABC 中,∠A =85°,∠B =45°, ∠ACD是 △ABC的一个外角,你能求出∠ACD的度数吗?
85°
45°
50°
130°
∠ACD 与∠A,∠B 的大小有什么关系?
∠ACD =∠A +∠B
那么对于任意三角形的一个外角与它不相邻的两个内角是否都具有这种关系呢?
合作探究---三角形的外角的性质
如图,求证任意一个△ABC的外角∠BCD与其不相邻的两内角(∠A,∠B)的关系。
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
∵∠A+∠B+∠ACB=180°,∠BCD+∠ACB=180°
∴∠A+∠B=∠BCD.
你能用作平行线的方法证明此结论吗?
合作探究---三角形的外角的性质
D
证明:过C作CE平行于AB,
A
B
C
1
2
∴∠1= ∠B,(两直线平行,同位角相等)
∠2= ∠A , (两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B.
E
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
合作探究---三角形的外角的性质
★三角形内角和定理的推论:
A
B
C
D
(
(
(
三角形的外角等于与它不相邻的两个内角的和.
★符号语言:
∵ ∠ACD是△ABC的一个外角
∴ ∠ACD= ∠A+ ∠B.
小试牛刀
2.如图,将三角尺的直角顶点放在直尺的一边上,∠1=20°,∠2=50°,则∠3的度数为_______.
30°
1.如图,△ABC中,延长BC至点D,∠B=20°,
∠ACD=120°,则∠A的大小为( )
A.120° B.90°
C.100° D.30°
C
A
B
D
C
小试牛刀
3、如图,∠A=60°,∠ABD=28°,∠ACE=20°,求∠BFC的度数.
∵ ∠BEC是△AEC的一个外角,
∴ ∠BEC= ∠A+∠ACE=80°,
∵ ∠BFC是△BEF的一个外角,
∴ ∠BFC= ∠ABD+ ∠BEF=108°
解:
F
A
C
D
E
B
你还有别的证明方法吗?
小试牛刀
4.如图,∠BAE,∠CBF,∠ACD 是△ABC 的三个外角,它们的和是多少?
解:∵∠BAE =∠2 +∠3,
∠CBF =∠1 +∠3,
∠ACD =∠1 +∠2,
∴∠BAE +∠CBF +∠ACD
= 2(∠1 +∠2 +∠3)
= 2×180°=360°.
总结:三角形的外角和等于360°
你还有其他
解法吗?
小试牛刀
解法二:如图,∠BAE+∠1=180 ° ① ,
∠CBF +∠2=180 ° ②,
∠ACD +∠3=180 ° ③,
又知∠1+ ∠2+ ∠3=180 °,
①+ ②+ ③得
∠BAE+ ∠CBF+ ∠ACD+(∠1+ ∠2+ ∠3)=540 °,
所以∠BAE+ ∠CBF+ ∠ACD=540 °-180°=360°.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
实战演练
1.如图,平面上直线a、b分别经过线段OK,则a、b相交所成的锐角
是( )
O
100°
70°
K
A.30°
B.20°
C.80°
D.70°
A
a
b
实战演练
2.如图,直线a ∥ b,c、d是截线且交于点A,若∠1=60°,∠2=100°,则∠A=( )
A. 40° B. 50°
C. 60° D. 70°
3.如图,CE是△ABC 的外角∠ACD的平分线,
若∠B=35°,∠ACE=60°,则∠A=( )
A. 35° B. 95° C. 85° D.75°
A
A
C
E
35°
60°
B
D
C
b
a
c
d
1
2
实战演练
4.如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边BC上的E处,折痕为CD,则∠EDB= .
5.如图,∠BAC=46°,∠B=27°,∠C=34°,则∠BDC= .
10°
107°
实战演练
1
2
3
B
A
C
P
N
M
D
E
F
6.如图,试求出∠A+∠B+∠C+∠D+∠E+∠F=_______.
360°
实战演练
7.如图,在△ABC中,∠B=∠C,点F为AC上一点,FD⊥BC于D,过D点作DE⊥AB于E.若∠AFD=150°,求∠EDF的度数.
解:∵∠AFD=∠FDC+∠C=90°+∠C,
∴∠C=∠AFD-90°=60°,
∵∠EDC=∠EDF+∠FDC,
∠EDC=∠B+∠BED,
∴90°+∠EDF=90°+∠B,
∴∠EDF=∠B,又∠B=∠C,
∴∠EDF=∠C=60°
拓展创新
在△ABC中,∠A=60°.
(1)如图1,∠ABC和∠ACB的平分线相交于点P,求∠BPC的度数.
(2)如图2,∠ACD是△ABC的外角, ∠ABC和∠ACD的平分线相交于点P,求∠BPC的度数.
(3)如图3,△ABC的外角∠CBD和∠BCE的平分线相交于点P,求∠BPC的度数.
A
P
B
图1
C
A
P
B
图2
C
D
拓展创新
解:(1)∠BPC=120°
(2)∠BPC=30°
(3)∠BPC=60°
A
P
B
图3
C
D
E
课堂总结
今天我们收获了哪些知识?
(畅所欲言)
1. 三角形的外角与不相邻的两个内角有什么关系?
2.这个推论是如何证明的?
3、三角形的外角和是多少?
课后作业
教材17页习题11.2第5、6、8题.
https://www.21cnjy.com/help/help_extract.php
人教版 八年级数学上
11.2.2 三角形的外角
学习目标
1.掌握三角形的外角的概念并能在能够复杂图形中找出外角.(难点)
3.掌握三角形的外角的性质,并利用其解决有关计算、推理问题(重、难点).
温故知新
1.在△ABC中,∠A=50°, ∠B=40°,则∠C= .
90 °
2.如图,在△ABC中, ∠A=85°, ∠B=45°,
则∠ACB= ,∠ACD= .
A
B
C
D
50 °
130°
合作探究---三角形的外角的概念
定义
如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
∠ACD是△ABC的一个外角
C
B
A
D
思考2、如图,∠ACD与∠BCE有什么关系?在三角形的每个顶点处有多少个外角?
思考1 、如图,延长AC到E,∠BCE是不是△ABC的一个外角?∠DCE是不是△ABC的一个外角?
E
在三角形每个顶点处都有两个外角.
∠ACD 与∠BCE为对顶角,∠ACD =∠BCE;
C
B
A
D
∠BCE是△ABC的一个外角,∠DCE不是△ABC的一个外角.
合作探究---三角形的外角的概念
合作探究---三角形的外角的概念
A
B
C
思考3、画出△ABC的所有外角,共有几个呢
每一个三角形都有6个外角.
每一个顶点相对应的外角都有
2个,且这2个角为对顶角.
小试牛刀
1.如图,下列各角是△ABC的外角的是( )
A.∠4
B.∠3
C.∠2
D.∠1
2.若三角形的一个外角等于和它相邻的内角,则这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.都有可能
B
B
小试牛刀
F
A
B
C
D
E
3、如图,∠ BEC是哪个三角形的外角?∠AEC是哪个三角形的外角?∠EFD是哪个三角形的外角?
∠BEC是△AEC的外角;
∠AEC是△BEC的外角;
∠EFD是△BEF和△DCF的外角.
合作探究---三角形的外角的性质
在△ABC 中,∠A =85°,∠B =45°, ∠ACD是 △ABC的一个外角,你能求出∠ACD的度数吗?
85°
45°
50°
130°
∠ACD 与∠A,∠B 的大小有什么关系?
∠ACD =∠A +∠B
那么对于任意三角形的一个外角与它不相邻的两个内角是否都具有这种关系呢?
合作探究---三角形的外角的性质
如图,求证任意一个△ABC的外角∠BCD与其不相邻的两内角(∠A,∠B)的关系。
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
∵∠A+∠B+∠ACB=180°,∠BCD+∠ACB=180°
∴∠A+∠B=∠BCD.
你能用作平行线的方法证明此结论吗?
合作探究---三角形的外角的性质
D
证明:过C作CE平行于AB,
A
B
C
1
2
∴∠1= ∠B,(两直线平行,同位角相等)
∠2= ∠A , (两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B.
E
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
合作探究---三角形的外角的性质
★三角形内角和定理的推论:
A
B
C
D
(
(
(
三角形的外角等于与它不相邻的两个内角的和.
★符号语言:
∵ ∠ACD是△ABC的一个外角
∴ ∠ACD= ∠A+ ∠B.
小试牛刀
2.如图,将三角尺的直角顶点放在直尺的一边上,∠1=20°,∠2=50°,则∠3的度数为_______.
30°
1.如图,△ABC中,延长BC至点D,∠B=20°,
∠ACD=120°,则∠A的大小为( )
A.120° B.90°
C.100° D.30°
C
A
B
D
C
小试牛刀
3、如图,∠A=60°,∠ABD=28°,∠ACE=20°,求∠BFC的度数.
∵ ∠BEC是△AEC的一个外角,
∴ ∠BEC= ∠A+∠ACE=80°,
∵ ∠BFC是△BEF的一个外角,
∴ ∠BFC= ∠ABD+ ∠BEF=108°
解:
F
A
C
D
E
B
你还有别的证明方法吗?
小试牛刀
4.如图,∠BAE,∠CBF,∠ACD 是△ABC 的三个外角,它们的和是多少?
解:∵∠BAE =∠2 +∠3,
∠CBF =∠1 +∠3,
∠ACD =∠1 +∠2,
∴∠BAE +∠CBF +∠ACD
= 2(∠1 +∠2 +∠3)
= 2×180°=360°.
总结:三角形的外角和等于360°
你还有其他
解法吗?
小试牛刀
解法二:如图,∠BAE+∠1=180 ° ① ,
∠CBF +∠2=180 ° ②,
∠ACD +∠3=180 ° ③,
又知∠1+ ∠2+ ∠3=180 °,
①+ ②+ ③得
∠BAE+ ∠CBF+ ∠ACD+(∠1+ ∠2+ ∠3)=540 °,
所以∠BAE+ ∠CBF+ ∠ACD=540 °-180°=360°.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
实战演练
1.如图,平面上直线a、b分别经过线段OK,则a、b相交所成的锐角
是( )
O
100°
70°
K
A.30°
B.20°
C.80°
D.70°
A
a
b
实战演练
2.如图,直线a ∥ b,c、d是截线且交于点A,若∠1=60°,∠2=100°,则∠A=( )
A. 40° B. 50°
C. 60° D. 70°
3.如图,CE是△ABC 的外角∠ACD的平分线,
若∠B=35°,∠ACE=60°,则∠A=( )
A. 35° B. 95° C. 85° D.75°
A
A
C
E
35°
60°
B
D
C
b
a
c
d
1
2
实战演练
4.如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边BC上的E处,折痕为CD,则∠EDB= .
5.如图,∠BAC=46°,∠B=27°,∠C=34°,则∠BDC= .
10°
107°
实战演练
1
2
3
B
A
C
P
N
M
D
E
F
6.如图,试求出∠A+∠B+∠C+∠D+∠E+∠F=_______.
360°
实战演练
7.如图,在△ABC中,∠B=∠C,点F为AC上一点,FD⊥BC于D,过D点作DE⊥AB于E.若∠AFD=150°,求∠EDF的度数.
解:∵∠AFD=∠FDC+∠C=90°+∠C,
∴∠C=∠AFD-90°=60°,
∵∠EDC=∠EDF+∠FDC,
∠EDC=∠B+∠BED,
∴90°+∠EDF=90°+∠B,
∴∠EDF=∠B,又∠B=∠C,
∴∠EDF=∠C=60°
拓展创新
在△ABC中,∠A=60°.
(1)如图1,∠ABC和∠ACB的平分线相交于点P,求∠BPC的度数.
(2)如图2,∠ACD是△ABC的外角, ∠ABC和∠ACD的平分线相交于点P,求∠BPC的度数.
(3)如图3,△ABC的外角∠CBD和∠BCE的平分线相交于点P,求∠BPC的度数.
A
P
B
图1
C
A
P
B
图2
C
D
拓展创新
解:(1)∠BPC=120°
(2)∠BPC=30°
(3)∠BPC=60°
A
P
B
图3
C
D
E
课堂总结
今天我们收获了哪些知识?
(畅所欲言)
1. 三角形的外角与不相邻的两个内角有什么关系?
2.这个推论是如何证明的?
3、三角形的外角和是多少?
课后作业
教材17页习题11.2第5、6、8题.
https://www.21cnjy.com/help/help_extract.php
