北师大版五年级上册数学整理与复习(2)(课件)(共20张PPT)
文档属性
| 名称 | 北师大版五年级上册数学整理与复习(2)(课件)(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-22 17:01:49 | ||
图片预览




文档简介
(共20张PPT)
轴对称和平移
整理与复习(二)
这一单元我们都学习了什么呢?
轴对称再认识
平移
欣赏与设计
轴
对
称
图
形
的
特
征
找
对
称
轴
平
移
运
动
的
特
征
画
平
移
后
的
图
形
轴
对
称
法
设
计
图
案
画
轴
对
称
图
形
平
移
法
设
计
图
案
轴对称和平移
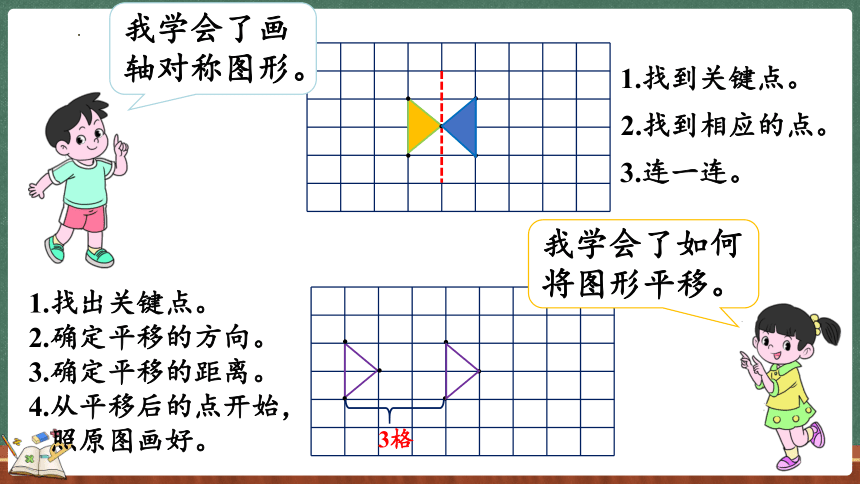
1.找到关键点。
2.找到相应的点。
3.连一连。
3格
1.找出关键点。
2.确定平移的方向。
3.确定平移的距离。
4.从平移后的点开始,
照原图画好。
我学会了如何将图形平移。
我学会了画轴对称图形。
我的成长足迹
?
我发现轴对称图形很有趣,对称轴两边的图形形状相同,但方向相反。平移改变图形位置,但不改变形状、大小。
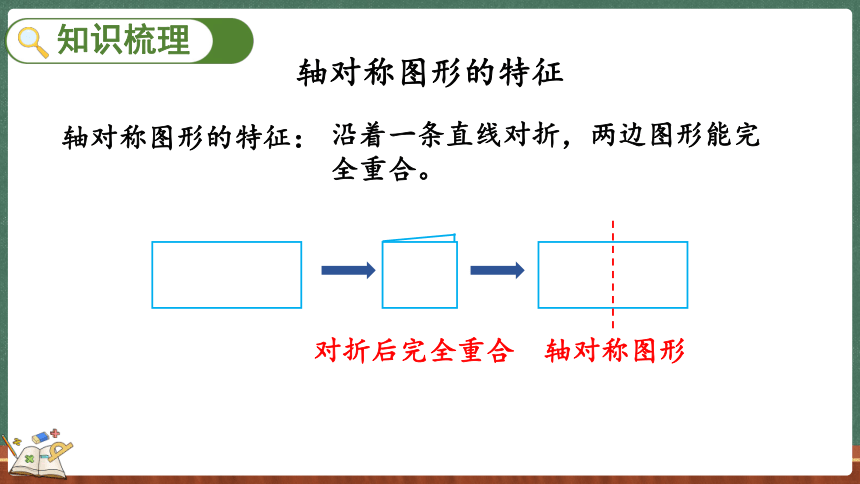
轴对称图形的特征:
沿着一条直线对折,两边图形能完全重合。
对折后完全重合
轴对称图形
轴对称图形的特征
找对称轴:
1.沿着一条直线对折,两边图形能
完全重合,这条直线就是对称轴。
2.有的轴对称图形只有一条对称轴,
有的有多条对称轴。
3.对称轴是一条直线。
2条对称轴
5条对称轴
找对称轴
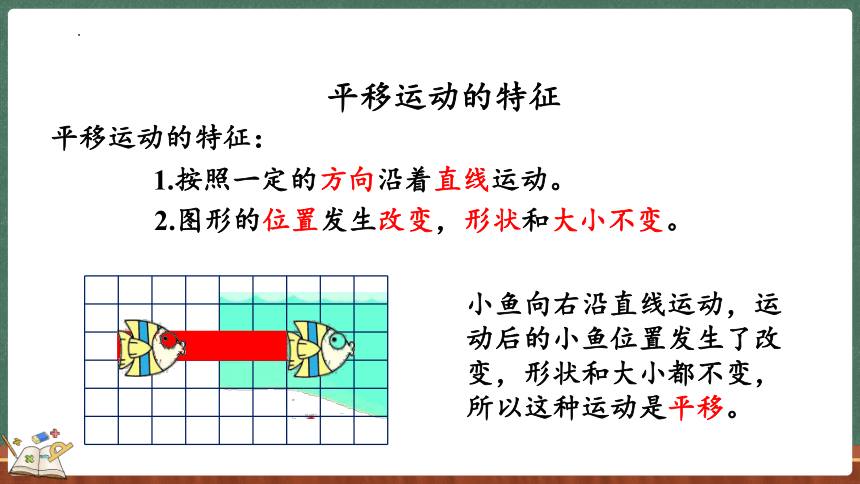
1.按照一定的方向沿着直线运动。
2.图形的位置发生改变,形状和大小不变。
平移运动的特征:
小鱼向右沿直线运动,运动后的小鱼位置发生了改变,形状和大小都不变,所以这种运动是平移。
平移运动的特征
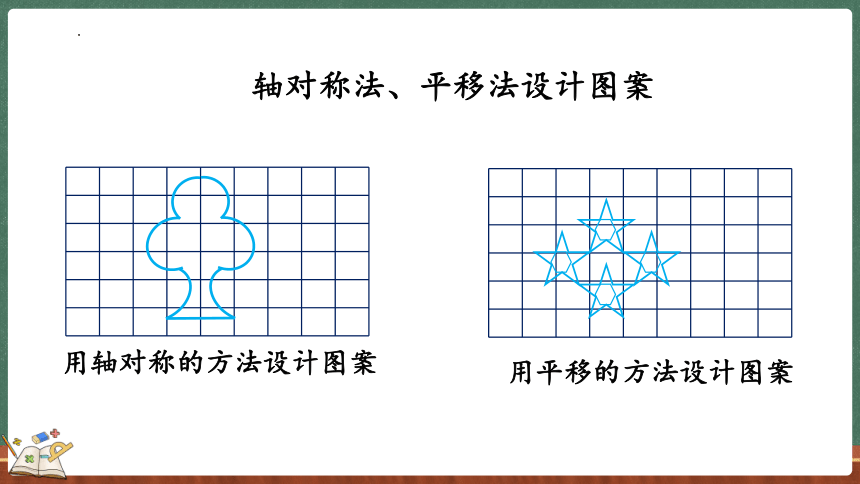
用轴对称的方法设计图案
用平移的方法设计图案
轴对称法、平移法设计图案
圆是轴对称图形吗?
圆是轴对称图形,沿着过圆心的任意一条直线对折,两边图形都能完全重合。
我提出的问题
?
请你结合前面的数学学习写一篇数学日记。
轴对称,这个听起来就充满对称美的概念,引领我走进了图形世界的另一番景象。我发现,许多我们日常生活中常见的事物,如蝴蝶的翅膀、脸谱、甚至是一些建筑设计,都蕴含着轴对称的奥秘。通过学习,我学会了如何判断一个图形是否是轴对称的,以及它的对称轴在哪里。这个过程中,我体会到了对称之美带来的视觉享受。
而平移,则是另一种让人着迷的图形变换方式。它像是一种魔法,让图形在不改变形状和大小的情况下,在平面内沿着某个方向“移动”起来。我意识到数学不仅仅是数字和公式的堆砌,它更是一种可以用来描述和解释现实世界的工具。
回顾这一单元的学习,我收获的不仅仅是轴对称和平移的知识,更重要的是,我学会了用数学的眼光去观察世界,用数学的思维去思考问题。我开始意识到,数学不仅仅是一门学科,更是一种思维方式,一种能够让我们更加深刻地理解和认识世界的工具。
我的数学日记
!
选自教材第47页巩固应用第8题
画对称轴
1.按要求画一画,并与同伴交流你是怎样画的。
沿着这条线对折,图形的两边能完全重合,这条线就是它的对称轴。
向上平移3格
1.按要求画一画,并与同伴交流你是怎样画的。
1.确定关键点。
2.按照平移的距离和方向找到对应点,再画一画。
选自教材第47页巩固应用第8题
画出关于虚线轴对称的图形
1.按要求画一画,并与同伴交流你是怎样画的。
1.确定关键点。
2.根据对称轴找到对应点,再连一连。
选自教材第47页巩固应用第8题
画出关于虚线轴对称的图形
1.按要求画一画,并与同伴交流你是怎样画的。
1.确定关键点。
2.根据对称轴找到对应点,再连一连。
选自教材第47页巩固应用第8题
1.想一想,填一填。
向( )平移( )格得到
向( )平移( )格得到
向( )平移( )格,再向( )平移( )格得到
下
左
下
4
5
3
右
4
2.画出下面各图形的对称轴。
3.将第一行的图形对折,能得出第二行的哪种图形?
连一连。
4.据说古代希腊有一位将军向当时的大学者海伦请教
一个问题:从A地出发到河边饮马,再到B地,怎样
走最近?如何确定饮马的地点?
如右图,因为点 A’是点 A 关于L的对称点,所以 AC 与A’C 是相等的。而 A’B 是一条线段,A’B是连接A’、B这两点间的所有线中最短的一条。所以 AC+CB=A’C+CB=A’B 也是最短的一条,点C就是所要找的饮马地点。
这节课有什么收获呢?
1.找到关键点。
2.找到相应的点。
3.连一连。
画轴对称图形
1.找出关键点。
2.确定平移的方向。
3.确定平移的距离。
4.从平移后的点开始,照原图画好。
画平移后的图形
轴对称再认识
平移
欣赏与设计
轴
对
称
图
形
的
特
征
找
对
称
轴
平
移
运
动
的
特
征
画
平
移
后
的
图
形
轴
对
称
法
设
计
图
案
画
轴
对
称
图
形
平
移
法
设
计
图
案
轴对称和平移
轴对称和平移
整理与复习(二)
这一单元我们都学习了什么呢?
轴对称再认识
平移
欣赏与设计
轴
对
称
图
形
的
特
征
找
对
称
轴
平
移
运
动
的
特
征
画
平
移
后
的
图
形
轴
对
称
法
设
计
图
案
画
轴
对
称
图
形
平
移
法
设
计
图
案
轴对称和平移
1.找到关键点。
2.找到相应的点。
3.连一连。
3格
1.找出关键点。
2.确定平移的方向。
3.确定平移的距离。
4.从平移后的点开始,
照原图画好。
我学会了如何将图形平移。
我学会了画轴对称图形。
我的成长足迹
?
我发现轴对称图形很有趣,对称轴两边的图形形状相同,但方向相反。平移改变图形位置,但不改变形状、大小。
轴对称图形的特征:
沿着一条直线对折,两边图形能完全重合。
对折后完全重合
轴对称图形
轴对称图形的特征
找对称轴:
1.沿着一条直线对折,两边图形能
完全重合,这条直线就是对称轴。
2.有的轴对称图形只有一条对称轴,
有的有多条对称轴。
3.对称轴是一条直线。
2条对称轴
5条对称轴
找对称轴
1.按照一定的方向沿着直线运动。
2.图形的位置发生改变,形状和大小不变。
平移运动的特征:
小鱼向右沿直线运动,运动后的小鱼位置发生了改变,形状和大小都不变,所以这种运动是平移。
平移运动的特征
用轴对称的方法设计图案
用平移的方法设计图案
轴对称法、平移法设计图案
圆是轴对称图形吗?
圆是轴对称图形,沿着过圆心的任意一条直线对折,两边图形都能完全重合。
我提出的问题
?
请你结合前面的数学学习写一篇数学日记。
轴对称,这个听起来就充满对称美的概念,引领我走进了图形世界的另一番景象。我发现,许多我们日常生活中常见的事物,如蝴蝶的翅膀、脸谱、甚至是一些建筑设计,都蕴含着轴对称的奥秘。通过学习,我学会了如何判断一个图形是否是轴对称的,以及它的对称轴在哪里。这个过程中,我体会到了对称之美带来的视觉享受。
而平移,则是另一种让人着迷的图形变换方式。它像是一种魔法,让图形在不改变形状和大小的情况下,在平面内沿着某个方向“移动”起来。我意识到数学不仅仅是数字和公式的堆砌,它更是一种可以用来描述和解释现实世界的工具。
回顾这一单元的学习,我收获的不仅仅是轴对称和平移的知识,更重要的是,我学会了用数学的眼光去观察世界,用数学的思维去思考问题。我开始意识到,数学不仅仅是一门学科,更是一种思维方式,一种能够让我们更加深刻地理解和认识世界的工具。
我的数学日记
!
选自教材第47页巩固应用第8题
画对称轴
1.按要求画一画,并与同伴交流你是怎样画的。
沿着这条线对折,图形的两边能完全重合,这条线就是它的对称轴。
向上平移3格
1.按要求画一画,并与同伴交流你是怎样画的。
1.确定关键点。
2.按照平移的距离和方向找到对应点,再画一画。
选自教材第47页巩固应用第8题
画出关于虚线轴对称的图形
1.按要求画一画,并与同伴交流你是怎样画的。
1.确定关键点。
2.根据对称轴找到对应点,再连一连。
选自教材第47页巩固应用第8题
画出关于虚线轴对称的图形
1.按要求画一画,并与同伴交流你是怎样画的。
1.确定关键点。
2.根据对称轴找到对应点,再连一连。
选自教材第47页巩固应用第8题
1.想一想,填一填。
向( )平移( )格得到
向( )平移( )格得到
向( )平移( )格,再向( )平移( )格得到
下
左
下
4
5
3
右
4
2.画出下面各图形的对称轴。
3.将第一行的图形对折,能得出第二行的哪种图形?
连一连。
4.据说古代希腊有一位将军向当时的大学者海伦请教
一个问题:从A地出发到河边饮马,再到B地,怎样
走最近?如何确定饮马的地点?
如右图,因为点 A’是点 A 关于L的对称点,所以 AC 与A’C 是相等的。而 A’B 是一条线段,A’B是连接A’、B这两点间的所有线中最短的一条。所以 AC+CB=A’C+CB=A’B 也是最短的一条,点C就是所要找的饮马地点。
这节课有什么收获呢?
1.找到关键点。
2.找到相应的点。
3.连一连。
画轴对称图形
1.找出关键点。
2.确定平移的方向。
3.确定平移的距离。
4.从平移后的点开始,照原图画好。
画平移后的图形
轴对称再认识
平移
欣赏与设计
轴
对
称
图
形
的
特
征
找
对
称
轴
平
移
运
动
的
特
征
画
平
移
后
的
图
形
轴
对
称
法
设
计
图
案
画
轴
对
称
图
形
平
移
法
设
计
图
案
轴对称和平移
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
