11.3.1多边形
图片预览



文档简介
(共21张PPT)
人教版 八年级数学上
11.3.1 多边形
学习目标
1.掌握多边形的定义及与多边形有关的概念,能将多边形按边分类.
2.掌握正多边形的概念.(重点)
3.理解多边形的对角线,能确定多边形对角线的条数.(难点)
情境导入
在实际生活当中,除了三角形,还有许多图形给我们以由一些线段围成的图形的形象,,比如房屋的结构、蜂巢结构等.观察图片,你能想象出由一些线段围成的图形吗?
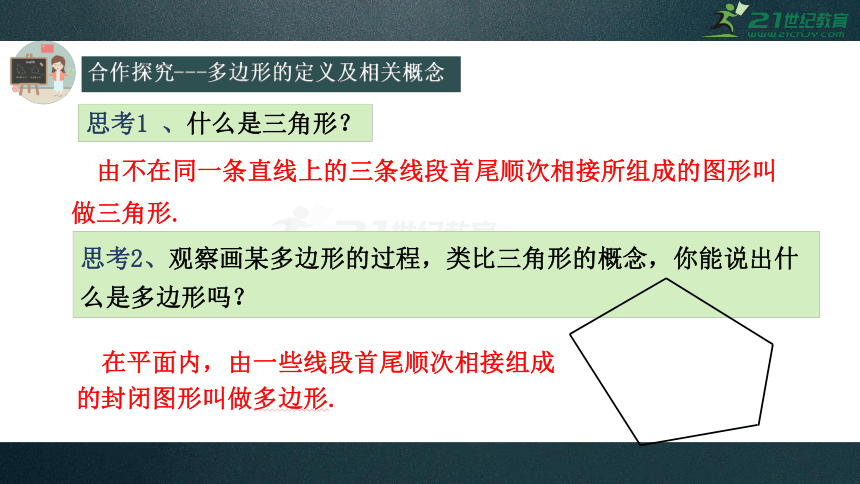
合作探究---多边形的定义及相关概念
思考2、观察画某多边形的过程,类比三角形的概念,你能说出什么是多边形吗?
在平面内,由一些线段首尾顺次相接组成
的封闭图形叫做多边形.
思考1 、什么是三角形?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫
做三角形.
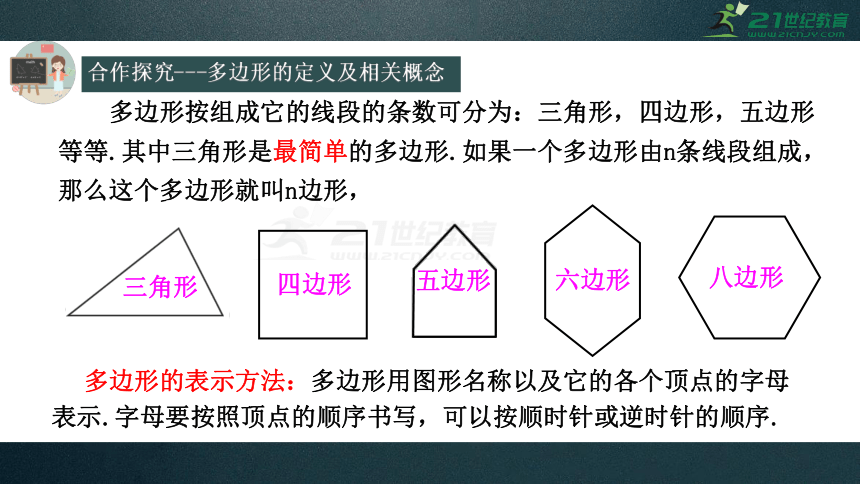
合作探究---多边形的定义及相关概念
四边形
五边形
六边形
八边形
多边形的表示方法:多边形用图形名称以及它的各个顶点的字母表示.字母要按照顶点的顺序书写,可以按顺时针或逆时针的顺序.
多边形按组成它的线段的条数可分为:三角形,四边形,五边形等等.其中三角形是最简单的多边形.如果一个多边形由n条线段组成,那么这个多边形就叫n边形,
三角形
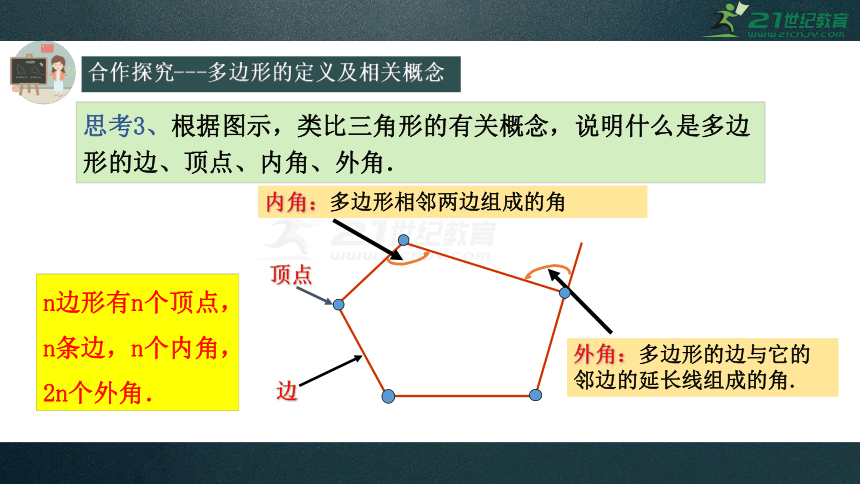
合作探究---多边形的定义及相关概念
内角:多边形相邻两边组成的角
思考3、根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角.
顶点
边
外角:多边形的边与它的邻边的延长线组成的角.
n边形有n个顶点,n条边,n个内角,2n个外角.
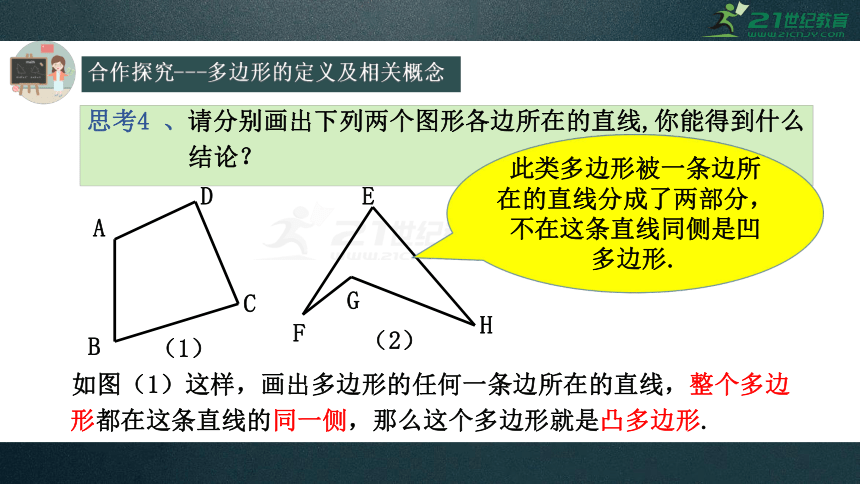
合作探究---多边形的定义及相关概念
思考4 、请分别画出下列两个图形各边所在的直线,你能得到什么
结论?
(1)
(2)
如图(1)这样,画出多边形的任何一条边所在的直线,整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形.
A
B
C
D
E
F
G
H
此类多边形被一条边所在的直线分成了两部分,不在这条直线同侧是凹多边形.
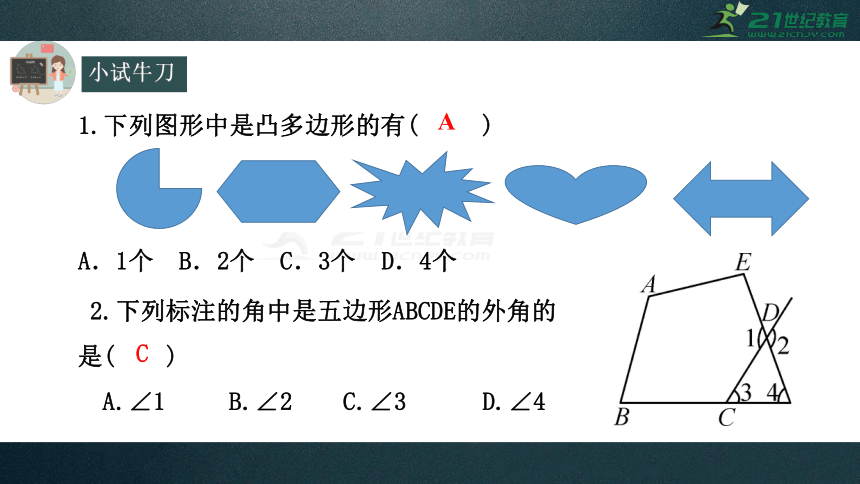
小试牛刀
1.下列图形中是凸多边形的有( )
A.1个 B.2个 C.3个 D.4个
A
2.下列标注的角中是五边形ABCDE的外角的是( )
A.∠1 B.∠2 C.∠3 D.∠4
C
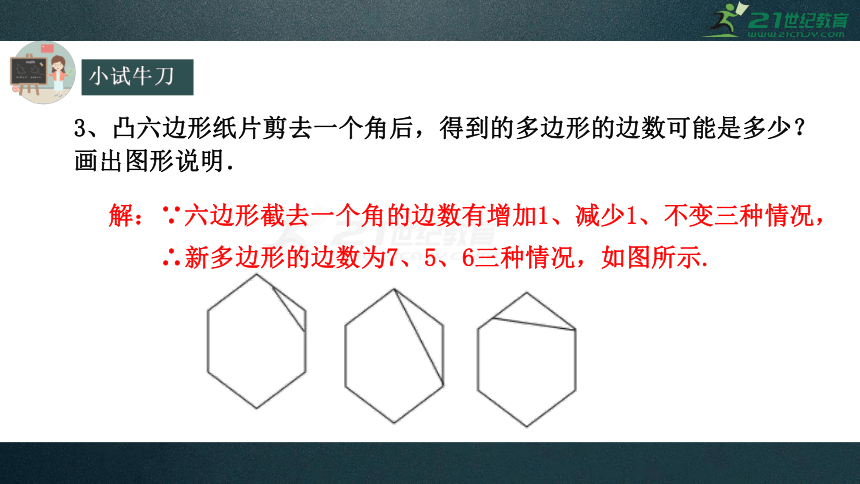
小试牛刀
3、凸六边形纸片剪去一个角后,得到的多边形的边数可能是多少?画出图形说明.
解:∵六边形截去一个角的边数有增加1、减少1、不变三种情况,
∴新多边形的边数为7、5、6三种情况,如图所示.
合作探究---多边形的对角线
你能画出它
其它的对角
线吗?
定义:
连接多边形不相邻的两个顶点的线段,
叫做多边形的对角线.
如图,线段AC、AD是五边形ABCDE的
一条对角线.
合作探究---多边形的对角线
三角形
六边形
四边形
八边形
……
五边形
思考5、画出下列图形从某一顶点发出的对角线的条数以及分割出的三角形个数:
多边形 三角形 四边形 五边形 六边形 八边形 n边形
从同一顶点引出的对角线的条数
分割出的三角形的个数
0
1
2
3
5
n-3
1
2
3
4
6
n-2
合作探究---多边形的对角线
n(n≥3)边形的一个顶点能引出(n-3)条对角线,把这个多边形分成(n-2)个三角形;一个n(n≥3)边形可以画出 条对角线。
归纳总结:
小试牛刀
1.若从多边形的一个顶点出发,最多可以画10条对角线,则
它是( )
A.十边形 B.十一边形 C.十二边形 D.十三边形
D
2.若过m边形的一个顶点有7条对角线,n边形没有对角线,则m+n= ____.
13
3.若一个多边形的边数是8,则它的对角线的条数比它的顶点数多( )
A.12 B.13 C.14 D.15
A
合作探究---正多边形的概念
定义:
像正方形这样,各个角都相等,各条边都相等的多边形.
正三角形
正方形
正五边形
正六边形
小试牛刀
1.下列图形中,是正多边形的是( )
A.等腰三角形 B.长方形 C.五边形 D. 正方形
2.下列说法错误的是( )
A.正多边形的各条边都相等
B.正多边形的各个角都相等
C.各个角都相等的多边形不一定是正多边形
D.各条边都相等的多边形一定是正多边形
D
D
实战演练
1.一个多边形共有20条对角线,则这个多边形的边数为( )
A.6 B.7 C.8 D.9
C
2.如图所示的多边形,下列说法不正确的是( )
A.多边形ABCDE是五边形,∠1、∠2、∠3是3个外角
B.该多边形表示为五边形ABCDE,∠1、∠2、∠3是它的角
C.该多边形是五边形,它的内角是∠A、∠B、∠BCD、∠CDE、∠AED
D.五边形ABCDE是凸五边形,∠1、∠2、∠3是3个外角
B
C
M
N
B
A
E
D
1
2
3
实战演练
3.若一个正n边形的边长是2cm,则它的周长为 cm.
2n
4.多边形的一个顶点的所有对角线的条数与这些对角线分该多边形所得三角形的个数的和为21,求这个多边形的边数.
解:设这个多边形为n边形,则有(n-3)条对角线,所分得的三角形个数为n-2,
∴n-3+n-2=21,
解得n=13.
答:该多边形的边数有13条.
拓展创新
已知从n边形的一个顶点出发共有4条对角线,其周长为56,且各边长是连续的自然数,求这个多边形的各边之长.
解:∵n-3=4, ∴n=7,
设最小边长为x,则其余边长为x+1,x+2,x+3,x+4,
x+5,x+6,可列方程,
x+x+1+x+2+x+3+x+4+x+5+x+6=56,解得x=5,
∴ x+1=6,x+2=7,x+3=8,x+4=9,x+5=10,
x+6=11,
即多边形的边长分别为5,6,7,8,9,10,11.
课堂小结
今天我们收获了哪些知识?(畅所欲言)
1. 什么是多边形的内角?外角?对角线?
2.多边形的对角线有什么特点呢?
3.正多边形有什么特点呢?
课后作业
教材21页练习第1、2题.
https://www.21cnjy.com/help/help_extract.php
人教版 八年级数学上
11.3.1 多边形
学习目标
1.掌握多边形的定义及与多边形有关的概念,能将多边形按边分类.
2.掌握正多边形的概念.(重点)
3.理解多边形的对角线,能确定多边形对角线的条数.(难点)
情境导入
在实际生活当中,除了三角形,还有许多图形给我们以由一些线段围成的图形的形象,,比如房屋的结构、蜂巢结构等.观察图片,你能想象出由一些线段围成的图形吗?
合作探究---多边形的定义及相关概念
思考2、观察画某多边形的过程,类比三角形的概念,你能说出什么是多边形吗?
在平面内,由一些线段首尾顺次相接组成
的封闭图形叫做多边形.
思考1 、什么是三角形?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫
做三角形.
合作探究---多边形的定义及相关概念
四边形
五边形
六边形
八边形
多边形的表示方法:多边形用图形名称以及它的各个顶点的字母表示.字母要按照顶点的顺序书写,可以按顺时针或逆时针的顺序.
多边形按组成它的线段的条数可分为:三角形,四边形,五边形等等.其中三角形是最简单的多边形.如果一个多边形由n条线段组成,那么这个多边形就叫n边形,
三角形
合作探究---多边形的定义及相关概念
内角:多边形相邻两边组成的角
思考3、根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角.
顶点
边
外角:多边形的边与它的邻边的延长线组成的角.
n边形有n个顶点,n条边,n个内角,2n个外角.
合作探究---多边形的定义及相关概念
思考4 、请分别画出下列两个图形各边所在的直线,你能得到什么
结论?
(1)
(2)
如图(1)这样,画出多边形的任何一条边所在的直线,整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形.
A
B
C
D
E
F
G
H
此类多边形被一条边所在的直线分成了两部分,不在这条直线同侧是凹多边形.
小试牛刀
1.下列图形中是凸多边形的有( )
A.1个 B.2个 C.3个 D.4个
A
2.下列标注的角中是五边形ABCDE的外角的是( )
A.∠1 B.∠2 C.∠3 D.∠4
C
小试牛刀
3、凸六边形纸片剪去一个角后,得到的多边形的边数可能是多少?画出图形说明.
解:∵六边形截去一个角的边数有增加1、减少1、不变三种情况,
∴新多边形的边数为7、5、6三种情况,如图所示.
合作探究---多边形的对角线
你能画出它
其它的对角
线吗?
定义:
连接多边形不相邻的两个顶点的线段,
叫做多边形的对角线.
如图,线段AC、AD是五边形ABCDE的
一条对角线.
合作探究---多边形的对角线
三角形
六边形
四边形
八边形
……
五边形
思考5、画出下列图形从某一顶点发出的对角线的条数以及分割出的三角形个数:
多边形 三角形 四边形 五边形 六边形 八边形 n边形
从同一顶点引出的对角线的条数
分割出的三角形的个数
0
1
2
3
5
n-3
1
2
3
4
6
n-2
合作探究---多边形的对角线
n(n≥3)边形的一个顶点能引出(n-3)条对角线,把这个多边形分成(n-2)个三角形;一个n(n≥3)边形可以画出 条对角线。
归纳总结:
小试牛刀
1.若从多边形的一个顶点出发,最多可以画10条对角线,则
它是( )
A.十边形 B.十一边形 C.十二边形 D.十三边形
D
2.若过m边形的一个顶点有7条对角线,n边形没有对角线,则m+n= ____.
13
3.若一个多边形的边数是8,则它的对角线的条数比它的顶点数多( )
A.12 B.13 C.14 D.15
A
合作探究---正多边形的概念
定义:
像正方形这样,各个角都相等,各条边都相等的多边形.
正三角形
正方形
正五边形
正六边形
小试牛刀
1.下列图形中,是正多边形的是( )
A.等腰三角形 B.长方形 C.五边形 D. 正方形
2.下列说法错误的是( )
A.正多边形的各条边都相等
B.正多边形的各个角都相等
C.各个角都相等的多边形不一定是正多边形
D.各条边都相等的多边形一定是正多边形
D
D
实战演练
1.一个多边形共有20条对角线,则这个多边形的边数为( )
A.6 B.7 C.8 D.9
C
2.如图所示的多边形,下列说法不正确的是( )
A.多边形ABCDE是五边形,∠1、∠2、∠3是3个外角
B.该多边形表示为五边形ABCDE,∠1、∠2、∠3是它的角
C.该多边形是五边形,它的内角是∠A、∠B、∠BCD、∠CDE、∠AED
D.五边形ABCDE是凸五边形,∠1、∠2、∠3是3个外角
B
C
M
N
B
A
E
D
1
2
3
实战演练
3.若一个正n边形的边长是2cm,则它的周长为 cm.
2n
4.多边形的一个顶点的所有对角线的条数与这些对角线分该多边形所得三角形的个数的和为21,求这个多边形的边数.
解:设这个多边形为n边形,则有(n-3)条对角线,所分得的三角形个数为n-2,
∴n-3+n-2=21,
解得n=13.
答:该多边形的边数有13条.
拓展创新
已知从n边形的一个顶点出发共有4条对角线,其周长为56,且各边长是连续的自然数,求这个多边形的各边之长.
解:∵n-3=4, ∴n=7,
设最小边长为x,则其余边长为x+1,x+2,x+3,x+4,
x+5,x+6,可列方程,
x+x+1+x+2+x+3+x+4+x+5+x+6=56,解得x=5,
∴ x+1=6,x+2=7,x+3=8,x+4=9,x+5=10,
x+6=11,
即多边形的边长分别为5,6,7,8,9,10,11.
课堂小结
今天我们收获了哪些知识?(畅所欲言)
1. 什么是多边形的内角?外角?对角线?
2.多边形的对角线有什么特点呢?
3.正多边形有什么特点呢?
课后作业
教材21页练习第1、2题.
https://www.21cnjy.com/help/help_extract.php
