湘教版八年级下册(新)第2章《2.2.1 平行四边形的性质》课件(23张PPT)
文档属性
| 名称 | 湘教版八年级下册(新)第2章《2.2.1 平行四边形的性质》课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1003.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-31 08:02:07 | ||
图片预览





文档简介
课件23张PPT。2.2 平行四边形
2.2.1 平行四边形的性质
第1课时 平行四边形的边、角性质 做一做
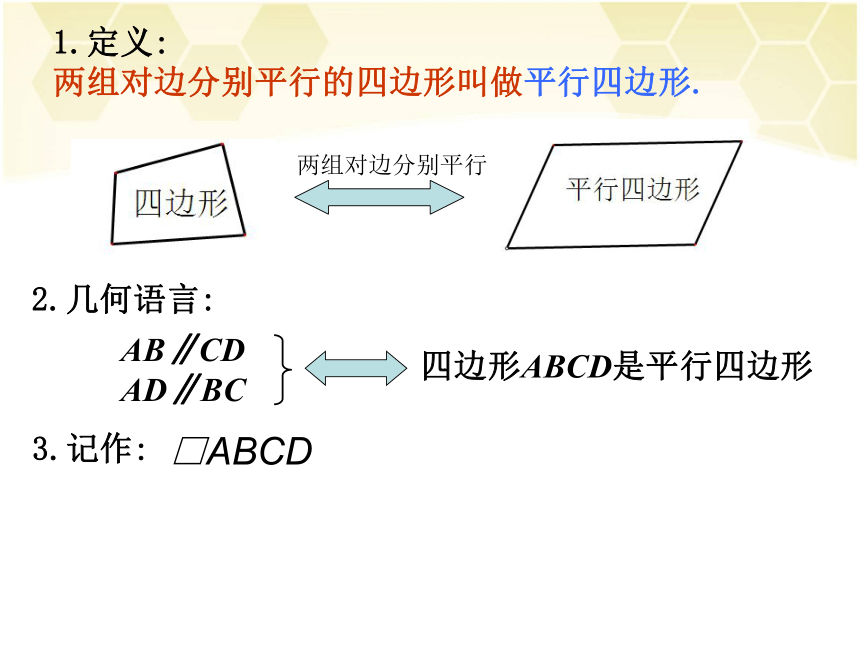
在小学,我们已经认识了平行四边形,在图中找出平行四边形,并把它们勾画出来.1.定义:
两组对边分别平行的四边形叫做平行四边形.3.记作: □ABCD2.几何语言:
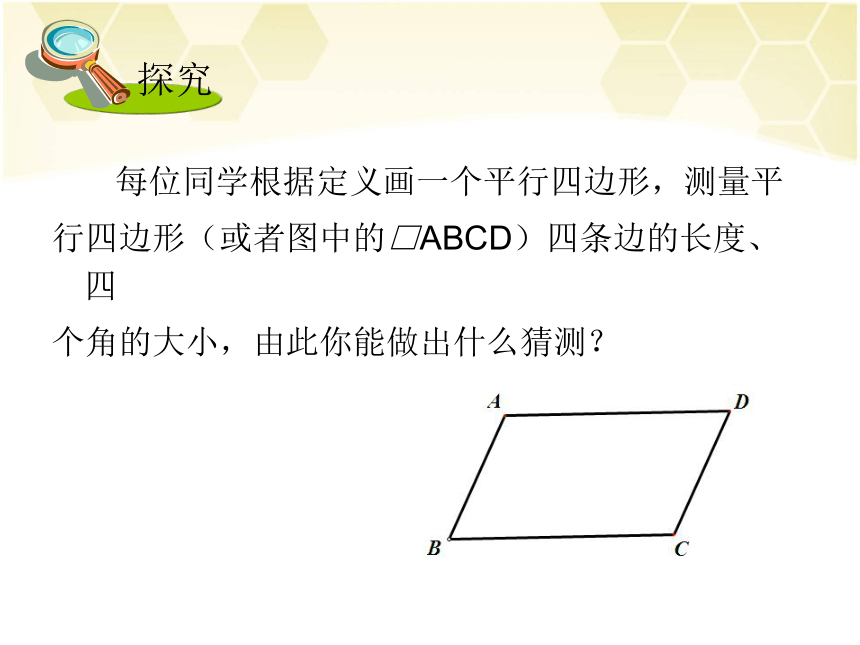
四边形ABCD是平行四边形AB∥CD AD∥BC两组对边分别平行 探究 每位同学根据定义画一个平行四边形,测量平
行四边形(或者图中的□ABCD)四条边的长度、四
个角的大小,由此你能做出什么猜测?
通过观察和测量,我发现平行四边形对边相等,对角相等.你能证明吗?下面我们来证明这个结论.如图,连接AC.
∵四边形ABCD为平行四边形,
∴AB∥DC,AD∥BC(平行四边形的两组对边分别平行).
∴∠1=∠2,∠3=∠4.
又AC=CA,
∴△ABC≌△CDA.
∴AB=CD,BC=DA,∠B=∠D.
又∠1+∠4=∠2+∠3,
∴∠BAD=∠DCB.
由此得到平行四边形的性质定理:
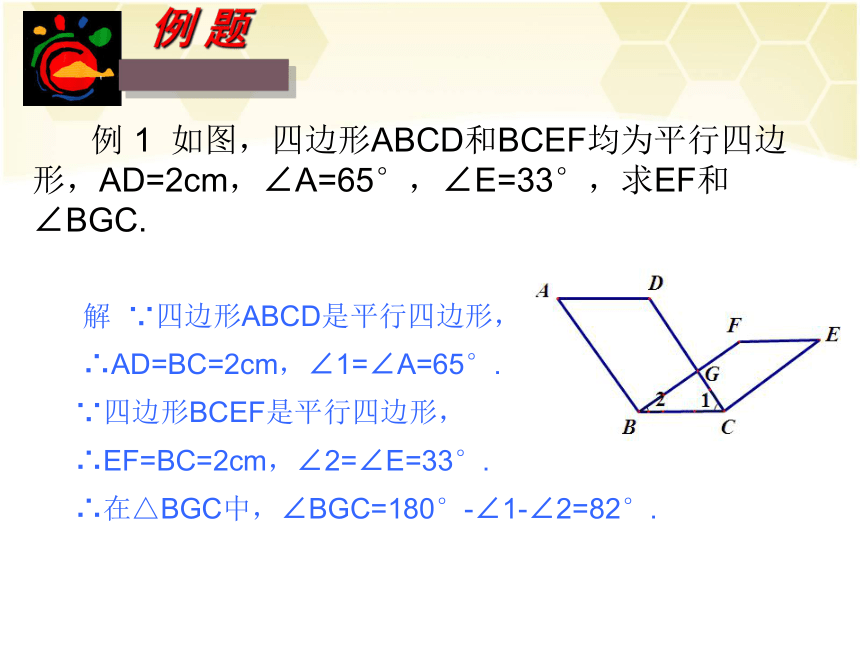
平行四边形的对边相等,平行四边形的对角相等. 例 1 如图,四边形ABCD和BCEF均为平行四边形,AD=2cm,∠A=65°,∠E=33°,求EF和∠BGC. 解 ∵四边形ABCD是平行四边形,
∴AD=BC=2cm,∠1=∠A=65°.
∵四边形BCEF是平行四边形,
∴EF=BC=2cm,∠2=∠E=33°.
∴在△BGC中,∠BGC=180°-∠1-∠2=82°. 例2 如图,直线 与 平行,AB,CD是 与 之间的任意两条平行线段.试问:AB与CD是否相等? 为什么
解:∵ ∥ ,AB∥CD,
∴四边形ABDC是平行四边形.
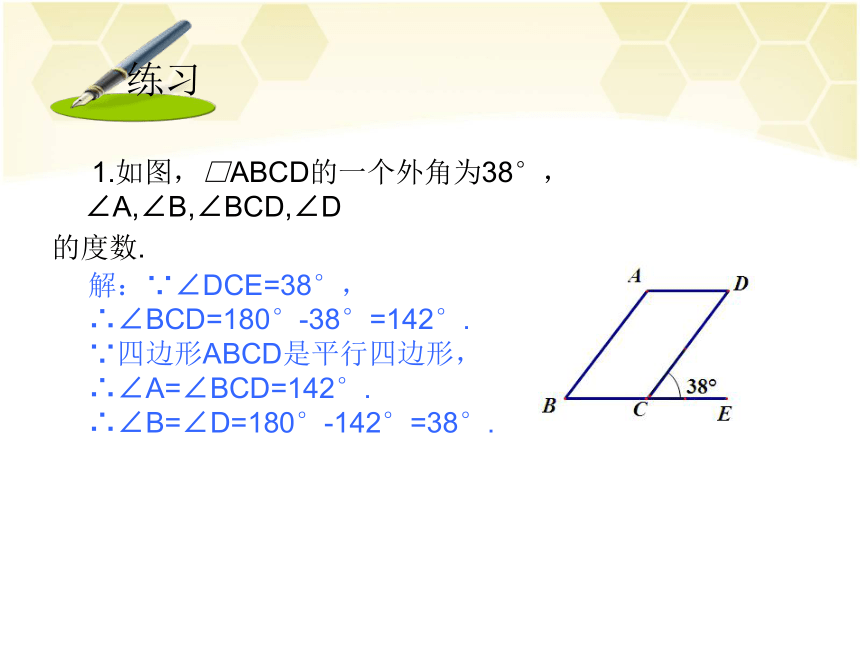
∴AB=CD. 练习 1.如图,□ABCD的一个外角为38°,∠A,∠B,∠BCD,∠D
的度数.解:∵∠DCE=38°,
∴∠BCD=180°-38°=142°.
∵四边形ABCD是平行四边形,
∴∠A=∠BCD=142°.
∴∠B=∠D=180°-142°=38°. 练习 2.如图,在□ABCD中,∠ABC=68°,BE平分∠ABC,
交AD于点E.AB=2cm,ED=1cm.
(1)求∠A,∠C,∠D的度数;
(2)求□ABCD的周长.
解(1)∵四边形ABCD是平行四边形,
∴∠ABC=∠D=68°.
∴∠A=∠C=180°-68°=112°.
(2)∵BE平分∠ABC,
∴∠ABE=∠EBC=∠BAE.
∴AB=AE=2cm.
∴AD=2+1=3(cm).
∴□ABCD的周长为:3+2+3+2=10(cm).
1. 概念:
四边形
两组对边分别平行
平行四边形
2. 性质: 性质一:对边平行,相等 性质二:对角相等,邻角互补 2.2.1 平行四边形的性质
第2课时 平行四边形的对角线的性质2.上节课我们掌握了平行四边
形的哪些性质?1.什么是平行四边形?平行四边形的性质:平行四边形的对边相等.平行四边形的对角相等.
1.对边:2.对角:∵四边形ABCD是平行四边形,
∴∠A=∠C , ∠B=∠D.
∵四边形ABCD是平行四边形,
∴AB=CD , AD=BC. 探究 如图,已知□ABCD两条对角线AC与BD相交于点O,比
较OA,OC,OB,OD的长度,有哪些线段相等?你能做出什么
猜测?
我发现OA=OC,
OB=OD.我猜测点O是
每条对角线的
中点.这个猜测正确吗?下面我们来进行证明.如图,
∵四边形ABCD是平行四边形
∴AB∥DC,AB∥DC,
∴∠1=∠2,∠3=∠4.
∴△OAB≌△OCD.
∴OA=OC,OB=OD.
由此得到平行四边形的性质定理:平行四边形的对角线互相平分. 例1 如图,在□ABCD中,对角线AC与BD相交于点O,AC=6,BD=10,CD=4.8.试求△COD的周长.解 ∵AC,BD为平行四边形ABCD的对角线,
∴OC= AC=3,OD= BD=5.
又∵CD=4.8,
∴△COD的周长为3+5+4.8=12.8. 例2 如图,在□ABCD中,对角线AC与BD相交与
点O,过点O的直线MN分别交AD,BC于点M,N.
求证:点O是线段MN的中点.
证明:∵AC,BD为□ABCD的对角线,且相交于点O,
∴OA=OC.
∵AD∥BC,
∴∠MAO=∠NCO.
又∠AOM=∠CON,
∴△AOM=△CON.
∴OM=ON.
∴点O是线段MN的中点. 练习 1.如图,在□ABCD中,BC=10cm,AC=8cm,
BD=14cm.
(1)求△AOD的周长;
(2)△ABC与△BCD的周长哪个长?长多少?解:(1)∵AC,BD为平行四边形
ABCD的对角线,
∴OA= AC=3,OD= BD=5.
△AOD的周长为:10+3+5=18(cm).
(2)△ABC与△BCD的周长相比△BCD的周长长,长6cm.
练习 2.平行四边形一条对角线的两个端点到另一条对角线的
距离相等吗?为什么?解:相等.理由如下:
如右图所示,已知□ABCD中两条对角线相交于O,过A作AE⊥BD,交BD于E,过C作CF⊥BD,交BD于F.
求证:AE=CF.
证明:∵四边形ABCD是平行四边形,
∴AO=OC,
∵AE⊥BD,CF⊥BD,
∴∠AEO=∠CFO=90°.
∵∠AOE=∠COF,
∴Rt△AEO=Rt△CFO(AAS).
∴AE=CF. 平行四边形的性质定理:
平行四边形的对角线互相平分.
2.2.1 平行四边形的性质
第1课时 平行四边形的边、角性质 做一做
在小学,我们已经认识了平行四边形,在图中找出平行四边形,并把它们勾画出来.1.定义:
两组对边分别平行的四边形叫做平行四边形.3.记作: □ABCD2.几何语言:
四边形ABCD是平行四边形AB∥CD AD∥BC两组对边分别平行 探究 每位同学根据定义画一个平行四边形,测量平
行四边形(或者图中的□ABCD)四条边的长度、四
个角的大小,由此你能做出什么猜测?
通过观察和测量,我发现平行四边形对边相等,对角相等.你能证明吗?下面我们来证明这个结论.如图,连接AC.
∵四边形ABCD为平行四边形,
∴AB∥DC,AD∥BC(平行四边形的两组对边分别平行).
∴∠1=∠2,∠3=∠4.
又AC=CA,
∴△ABC≌△CDA.
∴AB=CD,BC=DA,∠B=∠D.
又∠1+∠4=∠2+∠3,
∴∠BAD=∠DCB.
由此得到平行四边形的性质定理:
平行四边形的对边相等,平行四边形的对角相等. 例 1 如图,四边形ABCD和BCEF均为平行四边形,AD=2cm,∠A=65°,∠E=33°,求EF和∠BGC. 解 ∵四边形ABCD是平行四边形,
∴AD=BC=2cm,∠1=∠A=65°.
∵四边形BCEF是平行四边形,
∴EF=BC=2cm,∠2=∠E=33°.
∴在△BGC中,∠BGC=180°-∠1-∠2=82°. 例2 如图,直线 与 平行,AB,CD是 与 之间的任意两条平行线段.试问:AB与CD是否相等? 为什么
解:∵ ∥ ,AB∥CD,
∴四边形ABDC是平行四边形.
∴AB=CD. 练习 1.如图,□ABCD的一个外角为38°,∠A,∠B,∠BCD,∠D
的度数.解:∵∠DCE=38°,
∴∠BCD=180°-38°=142°.
∵四边形ABCD是平行四边形,
∴∠A=∠BCD=142°.
∴∠B=∠D=180°-142°=38°. 练习 2.如图,在□ABCD中,∠ABC=68°,BE平分∠ABC,
交AD于点E.AB=2cm,ED=1cm.
(1)求∠A,∠C,∠D的度数;
(2)求□ABCD的周长.
解(1)∵四边形ABCD是平行四边形,
∴∠ABC=∠D=68°.
∴∠A=∠C=180°-68°=112°.
(2)∵BE平分∠ABC,
∴∠ABE=∠EBC=∠BAE.
∴AB=AE=2cm.
∴AD=2+1=3(cm).
∴□ABCD的周长为:3+2+3+2=10(cm).
1. 概念:
四边形
两组对边分别平行
平行四边形
2. 性质: 性质一:对边平行,相等 性质二:对角相等,邻角互补 2.2.1 平行四边形的性质
第2课时 平行四边形的对角线的性质2.上节课我们掌握了平行四边
形的哪些性质?1.什么是平行四边形?平行四边形的性质:平行四边形的对边相等.平行四边形的对角相等.
1.对边:2.对角:∵四边形ABCD是平行四边形,
∴∠A=∠C , ∠B=∠D.
∵四边形ABCD是平行四边形,
∴AB=CD , AD=BC. 探究 如图,已知□ABCD两条对角线AC与BD相交于点O,比
较OA,OC,OB,OD的长度,有哪些线段相等?你能做出什么
猜测?
我发现OA=OC,
OB=OD.我猜测点O是
每条对角线的
中点.这个猜测正确吗?下面我们来进行证明.如图,
∵四边形ABCD是平行四边形
∴AB∥DC,AB∥DC,
∴∠1=∠2,∠3=∠4.
∴△OAB≌△OCD.
∴OA=OC,OB=OD.
由此得到平行四边形的性质定理:平行四边形的对角线互相平分. 例1 如图,在□ABCD中,对角线AC与BD相交于点O,AC=6,BD=10,CD=4.8.试求△COD的周长.解 ∵AC,BD为平行四边形ABCD的对角线,
∴OC= AC=3,OD= BD=5.
又∵CD=4.8,
∴△COD的周长为3+5+4.8=12.8. 例2 如图,在□ABCD中,对角线AC与BD相交与
点O,过点O的直线MN分别交AD,BC于点M,N.
求证:点O是线段MN的中点.
证明:∵AC,BD为□ABCD的对角线,且相交于点O,
∴OA=OC.
∵AD∥BC,
∴∠MAO=∠NCO.
又∠AOM=∠CON,
∴△AOM=△CON.
∴OM=ON.
∴点O是线段MN的中点. 练习 1.如图,在□ABCD中,BC=10cm,AC=8cm,
BD=14cm.
(1)求△AOD的周长;
(2)△ABC与△BCD的周长哪个长?长多少?解:(1)∵AC,BD为平行四边形
ABCD的对角线,
∴OA= AC=3,OD= BD=5.
△AOD的周长为:10+3+5=18(cm).
(2)△ABC与△BCD的周长相比△BCD的周长长,长6cm.
练习 2.平行四边形一条对角线的两个端点到另一条对角线的
距离相等吗?为什么?解:相等.理由如下:
如右图所示,已知□ABCD中两条对角线相交于O,过A作AE⊥BD,交BD于E,过C作CF⊥BD,交BD于F.
求证:AE=CF.
证明:∵四边形ABCD是平行四边形,
∴AO=OC,
∵AE⊥BD,CF⊥BD,
∴∠AEO=∠CFO=90°.
∵∠AOE=∠COF,
∴Rt△AEO=Rt△CFO(AAS).
∴AE=CF. 平行四边形的性质定理:
平行四边形的对角线互相平分.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
