湘教版八年级下册(新)第3章《3.1.1 平面直角坐标系》课件(19张PPT)
文档属性
| 名称 | 湘教版八年级下册(新)第3章《3.1.1 平面直角坐标系》课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 347.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-31 08:13:37 | ||
图片预览





文档简介
课件19张PPT。
第3章 图形与坐标
3.1 平面直角坐标系
1 平面直角坐标系 例如,李亮在教室里的座位可以简单地记作(4,2). 从上面的例子可以看到,为了确定物体在平面上的位置,我们经常用“第4组、第2排” 这样含有两个数的用语来确定物体的位置. 为了使这种方法更加简便,我们可以用一对有顺序的实数(简称为有序实数对)来表示.怎样用有序实数对来表示平面内点的位置呢? 为了用有序实数对表示平面内的一个点,可以在平面内画两条互相垂直的数轴,其中一条叫横轴(通常称x轴),另一条叫纵轴(通常称y轴),它们的交点O是这两条数轴的原点.
通常,我们取横轴向右为正方向,纵轴向上为正方向,横轴与纵轴的单位长度通常取成一致(有时也可以不一致),这样建立的两条数轴构成平面直角坐标系,记作Oxy.如下图. 从李亮在教室里的座位的例子可以看到,第4组是从横的方向来数的,第2排是从纵的方向来数的.
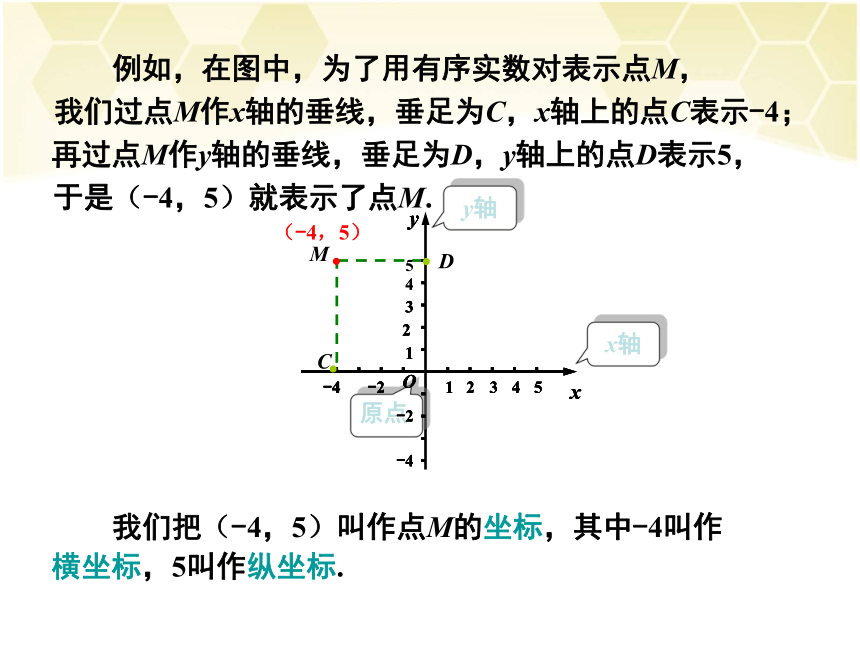
例如,在图中,为了用有序实数对表示点M, 我们过点M作x轴的垂线,垂足为C,x轴上的点C表示-4; 再过点M作y轴的垂线,垂足为D,y轴上的点D表示5, 于是(-4,5)就表示了点M. 我们把(-4,5)叫作点M的坐标,其中-4叫作
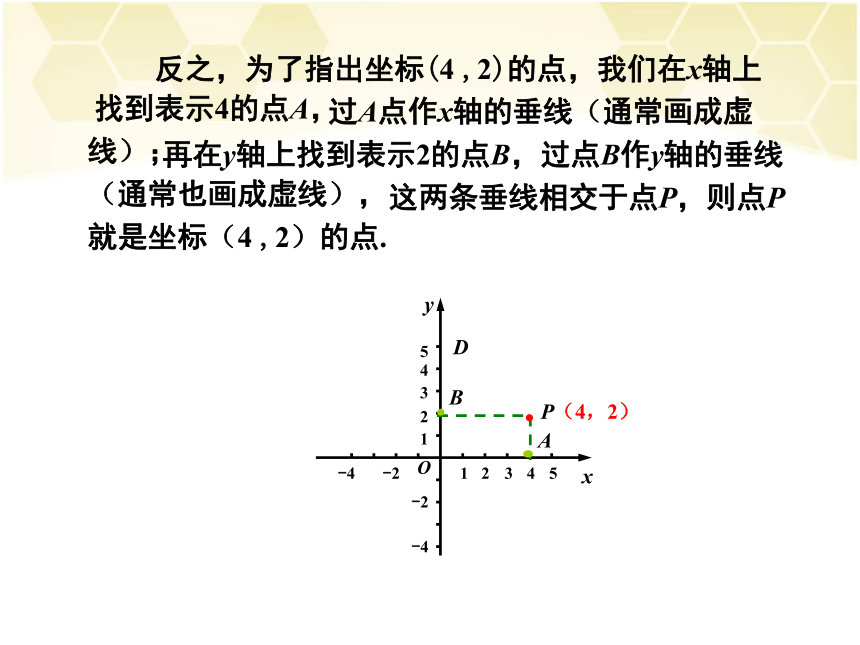
横坐标,5叫作纵坐标. 反之,为了指出坐标(4 ,2)的点,我们在x轴上找到表示4的点A,O13245-2-451234-2-4xyD 过A点作x轴的垂线(通常画成虚 线); 再在y轴上找到表示2的点B,过点B作y轴的垂线 (通常也画成虚线), 这两条垂线相交于点P,则点P 就是坐标(4 ,2)的点.(4,2) 在建立了平面直角坐标系后,平面上的点与有序实数对一一对应.综上所述, 在平面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图所示的Ⅰ,Ⅱ ,Ⅲ,Ⅳ四个区域,我们把这四个区域分别称为第一,二,三,四象限,坐标轴上的点不属于任何一个象限.
想一想,原点O的坐标是什么?x轴和y轴上的点的坐标有什么特征?如图,写出平面直角坐标系中点A ,B , C , D ,E,F的坐标.例1 结合例1、例2的解答,试说出平面直角坐标系中四个象限的点的坐标有什么特征,并填写下表:-++-+--+-做一做(1)说出点A,B,C,D,E的坐标.答:A的坐标为(3,3),
B的坐标为(-5 ,2),
C的坐标为(-4,-3),
D的坐标为(4,-3),
E的坐标为(5,0).(2)描出点P(-2,-1),Q(3,-2),S(2,5),
T(-4,3),分别指出各点所在的象限.答:点P在第三象限,点Q在第四象限,
点S在第一象限,点T在第二象限.
(3,-2)
3.1 平面直角坐标系
1 平面直角坐标系 例如,李亮在教室里的座位可以简单地记作(4,2). 从上面的例子可以看到,为了确定物体在平面上的位置,我们经常用“第4组、第2排” 这样含有两个数的用语来确定物体的位置. 为了使这种方法更加简便,我们可以用一对有顺序的实数(简称为有序实数对)来表示.怎样用有序实数对来表示平面内点的位置呢? 为了用有序实数对表示平面内的一个点,可以在平面内画两条互相垂直的数轴,其中一条叫横轴(通常称x轴),另一条叫纵轴(通常称y轴),它们的交点O是这两条数轴的原点.
通常,我们取横轴向右为正方向,纵轴向上为正方向,横轴与纵轴的单位长度通常取成一致(有时也可以不一致),这样建立的两条数轴构成平面直角坐标系,记作Oxy.如下图. 从李亮在教室里的座位的例子可以看到,第4组是从横的方向来数的,第2排是从纵的方向来数的.
例如,在图中,为了用有序实数对表示点M, 我们过点M作x轴的垂线,垂足为C,x轴上的点C表示-4; 再过点M作y轴的垂线,垂足为D,y轴上的点D表示5, 于是(-4,5)就表示了点M. 我们把(-4,5)叫作点M的坐标,其中-4叫作
横坐标,5叫作纵坐标. 反之,为了指出坐标(4 ,2)的点,我们在x轴上找到表示4的点A,O13245-2-451234-2-4xyD 过A点作x轴的垂线(通常画成虚 线); 再在y轴上找到表示2的点B,过点B作y轴的垂线 (通常也画成虚线), 这两条垂线相交于点P,则点P 就是坐标(4 ,2)的点.(4,2) 在建立了平面直角坐标系后,平面上的点与有序实数对一一对应.综上所述, 在平面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图所示的Ⅰ,Ⅱ ,Ⅲ,Ⅳ四个区域,我们把这四个区域分别称为第一,二,三,四象限,坐标轴上的点不属于任何一个象限.
想一想,原点O的坐标是什么?x轴和y轴上的点的坐标有什么特征?如图,写出平面直角坐标系中点A ,B , C , D ,E,F的坐标.例1 结合例1、例2的解答,试说出平面直角坐标系中四个象限的点的坐标有什么特征,并填写下表:-++-+--+-做一做(1)说出点A,B,C,D,E的坐标.答:A的坐标为(3,3),
B的坐标为(-5 ,2),
C的坐标为(-4,-3),
D的坐标为(4,-3),
E的坐标为(5,0).(2)描出点P(-2,-1),Q(3,-2),S(2,5),
T(-4,3),分别指出各点所在的象限.答:点P在第三象限,点Q在第四象限,
点S在第一象限,点T在第二象限.
(3,-2)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
