湘教版八年级下册(新)第4章4.5.2 建立一次函数模型解决预测类型的实际问题课件(18张PPT)
文档属性
| 名称 | 湘教版八年级下册(新)第4章4.5.2 建立一次函数模型解决预测类型的实际问题课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-31 00:00:00 | ||
图片预览






文档简介
课件18张PPT。4.5 一次函数的应用
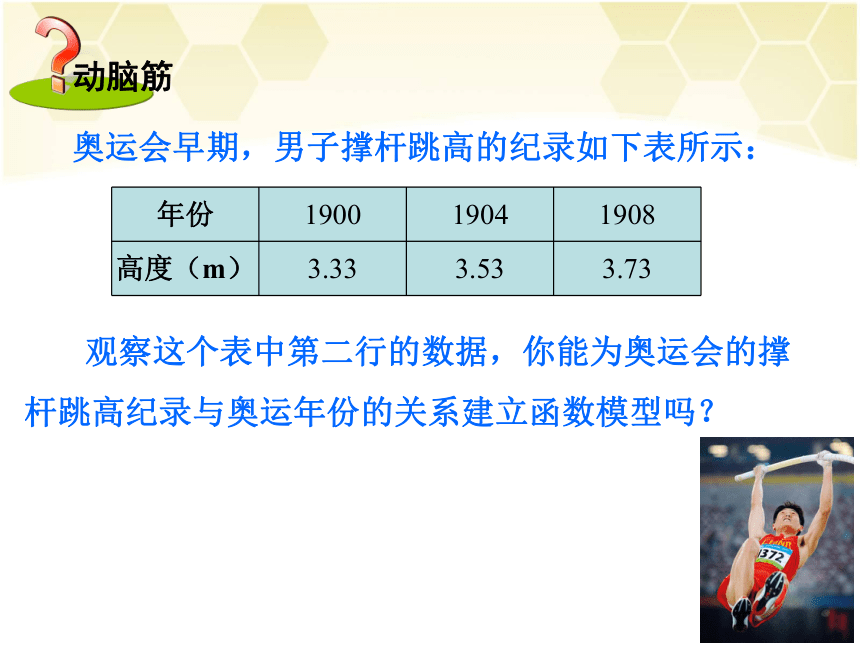
2 建立一次函数模型解决预测类型的实际问题 奥运会早期,男子撑杆跳高的纪录如下表所示:
观察这个表中第二行的数据,你能为奥运会的撑杆跳高纪录与奥运年份的关系建立函数模型吗? 上表中每一届比上一届的纪录提高了0.2m,可以
试着建立一次函数的模型.解得 b = 3.3, k=0.05.公式①就是奥运会早期男子撑杆跳高纪录y与时间t
的函数关系式.当t = 8时, y = 3.73,这说明1908年的撑杆跳高
纪录也符合公式①. 实际上,1912 年奥运会男子撑杆跳高纪录约为3.93 m. 这表明用所建立的函数模型,在已知数据邻近做预测,结果与实际情况比较吻合.y=0.05×12+3.33=3.93. 然而,1988年奥运会的男子撑杆跳高纪录是5.90 m,
远低于7.73 m. 这表明用所建立的函数模型远离已知数据
做预测是不可靠的.y=0.05×88+3.33=7.73.请每位同学伸出一只手掌,把大拇指与小拇指尽量张开,两指间的距离称为指距. 已知指距与身高具有如下关系:例2(1) 求身高y与指距x之间的函数表达式;
(2) 当李华的指距为22cm时,你能预测他的身高吗?(1) 求身高y与指距x之间的函数表达式;解得k = 9, b = -20.
于是y = 9x -20. ①将x = 21,y = 169代入①式也符合.
公式①就是身高y与指距x之间的函数表达式.解 当x = 22时, y = 9×22-20 = 178.
因此,李华的身高大约是178 cm.(2) 当李华的指距为22cm时,你能预测他的身高吗? (1)根据表中数据确定该一次函数的表达式;(2)如果蟋蟀1min叫了63次,那么该地当时的气温大约
为多少摄氏度? (3)能用所求出的函数模型来预测蟋蟀在0 ℃时所鸣叫的
次数吗? (1)根据表中数据确定该一次函数的表达式;(2)如果蟋蟀1min叫了63次,那么该地当时的气温大约
为多少摄氏度? (3) 能用所求出的函数模型来预测蟋蟀在0 ℃时所
鸣叫次数吗?答:不能,因为此函数关系是近似的,与实际
生活中的情况有所不符,蟋蟀在0 ℃时可能
不会鸣叫.2. 某商店今年7月初销售纯净水的数量如下表所示:(1)你能为销售纯净水的数量与时间之间的关系
建立函数模型吗?(2)用所求出的函数解析式预测今年7月5日该商店
销售纯净水的数量. 解 销售纯净水的数量y(瓶)与时间t的
函数关系式是
y= 160+(t-1)×5= 5t+155.(1)你能为销售纯净水的数量与时间之间的关系
建立函数模型吗?(2)用所求出的函数解析式预测今年7月5日该商店
销售纯净水的数量.
2 建立一次函数模型解决预测类型的实际问题 奥运会早期,男子撑杆跳高的纪录如下表所示:
观察这个表中第二行的数据,你能为奥运会的撑杆跳高纪录与奥运年份的关系建立函数模型吗? 上表中每一届比上一届的纪录提高了0.2m,可以
试着建立一次函数的模型.解得 b = 3.3, k=0.05.公式①就是奥运会早期男子撑杆跳高纪录y与时间t
的函数关系式.当t = 8时, y = 3.73,这说明1908年的撑杆跳高
纪录也符合公式①. 实际上,1912 年奥运会男子撑杆跳高纪录约为3.93 m. 这表明用所建立的函数模型,在已知数据邻近做预测,结果与实际情况比较吻合.y=0.05×12+3.33=3.93. 然而,1988年奥运会的男子撑杆跳高纪录是5.90 m,
远低于7.73 m. 这表明用所建立的函数模型远离已知数据
做预测是不可靠的.y=0.05×88+3.33=7.73.请每位同学伸出一只手掌,把大拇指与小拇指尽量张开,两指间的距离称为指距. 已知指距与身高具有如下关系:例2(1) 求身高y与指距x之间的函数表达式;
(2) 当李华的指距为22cm时,你能预测他的身高吗?(1) 求身高y与指距x之间的函数表达式;解得k = 9, b = -20.
于是y = 9x -20. ①将x = 21,y = 169代入①式也符合.
公式①就是身高y与指距x之间的函数表达式.解 当x = 22时, y = 9×22-20 = 178.
因此,李华的身高大约是178 cm.(2) 当李华的指距为22cm时,你能预测他的身高吗? (1)根据表中数据确定该一次函数的表达式;(2)如果蟋蟀1min叫了63次,那么该地当时的气温大约
为多少摄氏度? (3)能用所求出的函数模型来预测蟋蟀在0 ℃时所鸣叫的
次数吗? (1)根据表中数据确定该一次函数的表达式;(2)如果蟋蟀1min叫了63次,那么该地当时的气温大约
为多少摄氏度? (3) 能用所求出的函数模型来预测蟋蟀在0 ℃时所
鸣叫次数吗?答:不能,因为此函数关系是近似的,与实际
生活中的情况有所不符,蟋蟀在0 ℃时可能
不会鸣叫.2. 某商店今年7月初销售纯净水的数量如下表所示:(1)你能为销售纯净水的数量与时间之间的关系
建立函数模型吗?(2)用所求出的函数解析式预测今年7月5日该商店
销售纯净水的数量. 解 销售纯净水的数量y(瓶)与时间t的
函数关系式是
y= 160+(t-1)×5= 5t+155.(1)你能为销售纯净水的数量与时间之间的关系
建立函数模型吗?(2)用所求出的函数解析式预测今年7月5日该商店
销售纯净水的数量.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
