湘教版八年级下册(新)第5章5.1 频数与频率课件(23张PPT)
文档属性
| 名称 | 湘教版八年级下册(新)第5章5.1 频数与频率课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-31 10:33:12 | ||
图片预览








文档简介
课件23张PPT。
第5章 数据的频数分布
5.1 频数与频率 在前面的学习中,我们知道一组数据的平均数(中位数、众数)、方差反映了这组数据一般的、全局的性质,但这还不够,在许多实际问题中,我们还需要对收集的数据进行必要的归纳和整理,了解其分布情况,从而更具体地掌握这组数据. 请用整理数据的方法,借助统计图表将上述数据进行表述.可以采用“画记” 的方法得到下表:青年组(35 岁以下)中年组(35~50岁)老年组(50岁以上)正正正正 根据上表可以发现,青年组报名人数最多,中年组其次,
老年组最少. 我们把在不同小组中的数据个数称为频数.例如上表中20,17,13 分别是青年组、中年组、老年组的频数. 我们把每一组的频数与数据总数的比叫作这一组数据的频率,例如上表中青年组的频数为20, 频率为我们还可以用条形图(图1) 来表示各组人数. 图1前15 次射击得分情况后15 次射击得分情况(1) 用表格表示小芳射击训练中前15次和后15次射击得分
的频数和频率.
(2) 分别求出前15次和后15次射击得分的平均数(精确到
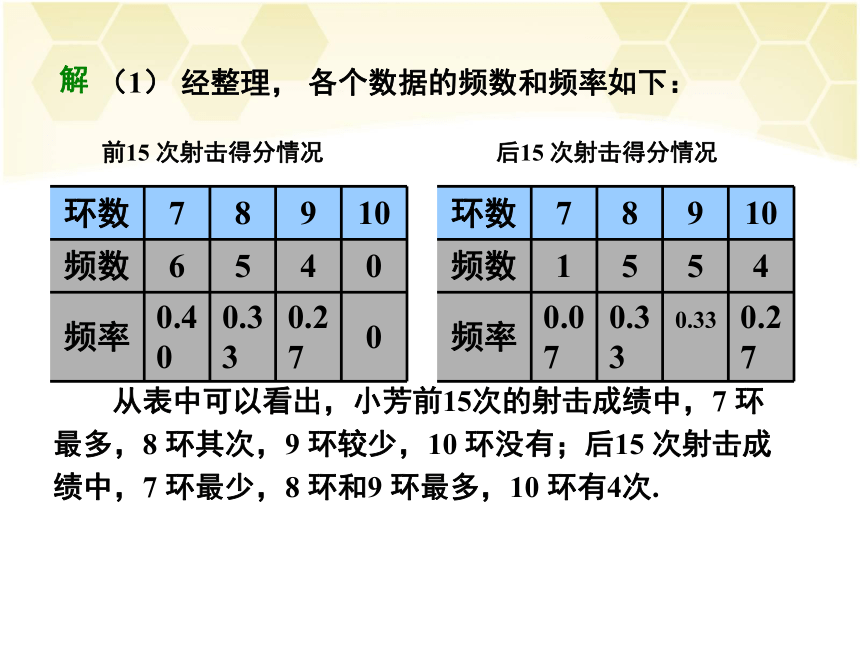
0.01),比较射击成绩的变化.前15 次射击得分情况0.33后15 次射击得分情况 从表中可以看出,小芳前15次的射击成绩中,7 环
最多,8 环其次,9 环较少,10 环没有;后15 次射击成
绩中,7 环最少,8 环和9 环最多,10 环有4次.
后15 次平均数大,说明经过调整射击方法后,
小芳得高分的次数增加,平均成绩得到了提高.同理可求得后15次射击成绩的平均数是8.80.(2) 前15次射击成绩的平均数是:解: 该班同学跳绳成绩统计表如下:(1) 按每分钟不足60 次为“不达标”, 60 ~ 90 次为“良”,
90 次以上为“优”, 编制成绩统计表(用频数和频率
表示).(2) 计算这个班的达标率.解: 由统计表数据可知该班同学跳绳达标率为
0.3+0.675=0.975. 一枚硬币有两面,我们称有国徽的一面为“正面”,
另一面为“反面”;掷一枚硬币,当硬币落下时,可能
出现“正面朝上”,也可能出现“反面朝上”.
每次掷币,两种情形必然出现一种,也只能出现一种. 究竟出现哪种情形,在掷币之前无法预计,只有掷币之后才能知道.与同桌同学合作,掷10次硬币,并把10次试验结果记录下来:(1) 计算“正面朝上” 和“反面朝上” 的频数各是多少,
它们之间有什么关系?
(2) 计算“正面朝上” 和“反面朝上” 的频率各是多少,
它们之间有什么关系?假设某同学掷10次硬币的结果如下:正正正正那么,出现“正面朝上” 的频数是4,频率为 ;
出现“反面朝上”的频数是6,频率为
可以发现,“正面朝上” 和“反面朝上” 的频数之和为试验总次数;而这两种情况的频率之和为1. 一般地,如果重复进行n次试验,某个试验结果
出现的次数m 称为这个试验结果在这n次实验中出现的频数,而频数与试验总次数的比 称为这个试验结果在这n次试验中出现的频率. 一次掷两枚硬币,用A,B,C分别代表可能发生的三种情形: A. 两枚硬币都是“正面朝上”; B. 两枚硬币都是“反面朝上”; C. 一枚硬币“正面朝上”,另一枚硬币“反面朝上”. 每次掷币都发生A,B,C三种情形中的一种,并且只发生一种. A,B,C发生的频数与频率 现在全班同学每人各掷两枚硬币5 次,记录所得结果, 将全班的结果汇总填入下表中,并计算频率.说一说,出现哪一种情形的频率高? 全班每组同学抛掷一枚硬币40 次,记录出现“正面朝上”
的结果,将各组试验结果汇总,完成下表:根据上表, 在下图中绘制“正面朝上” 的频率变化折线统计图.
5.1 频数与频率 在前面的学习中,我们知道一组数据的平均数(中位数、众数)、方差反映了这组数据一般的、全局的性质,但这还不够,在许多实际问题中,我们还需要对收集的数据进行必要的归纳和整理,了解其分布情况,从而更具体地掌握这组数据. 请用整理数据的方法,借助统计图表将上述数据进行表述.可以采用“画记” 的方法得到下表:青年组(35 岁以下)中年组(35~50岁)老年组(50岁以上)正正正正 根据上表可以发现,青年组报名人数最多,中年组其次,
老年组最少. 我们把在不同小组中的数据个数称为频数.例如上表中20,17,13 分别是青年组、中年组、老年组的频数. 我们把每一组的频数与数据总数的比叫作这一组数据的频率,例如上表中青年组的频数为20, 频率为我们还可以用条形图(图1) 来表示各组人数. 图1前15 次射击得分情况后15 次射击得分情况(1) 用表格表示小芳射击训练中前15次和后15次射击得分
的频数和频率.
(2) 分别求出前15次和后15次射击得分的平均数(精确到
0.01),比较射击成绩的变化.前15 次射击得分情况0.33后15 次射击得分情况 从表中可以看出,小芳前15次的射击成绩中,7 环
最多,8 环其次,9 环较少,10 环没有;后15 次射击成
绩中,7 环最少,8 环和9 环最多,10 环有4次.
后15 次平均数大,说明经过调整射击方法后,
小芳得高分的次数增加,平均成绩得到了提高.同理可求得后15次射击成绩的平均数是8.80.(2) 前15次射击成绩的平均数是:解: 该班同学跳绳成绩统计表如下:(1) 按每分钟不足60 次为“不达标”, 60 ~ 90 次为“良”,
90 次以上为“优”, 编制成绩统计表(用频数和频率
表示).(2) 计算这个班的达标率.解: 由统计表数据可知该班同学跳绳达标率为
0.3+0.675=0.975. 一枚硬币有两面,我们称有国徽的一面为“正面”,
另一面为“反面”;掷一枚硬币,当硬币落下时,可能
出现“正面朝上”,也可能出现“反面朝上”.
每次掷币,两种情形必然出现一种,也只能出现一种. 究竟出现哪种情形,在掷币之前无法预计,只有掷币之后才能知道.与同桌同学合作,掷10次硬币,并把10次试验结果记录下来:(1) 计算“正面朝上” 和“反面朝上” 的频数各是多少,
它们之间有什么关系?
(2) 计算“正面朝上” 和“反面朝上” 的频率各是多少,
它们之间有什么关系?假设某同学掷10次硬币的结果如下:正正正正那么,出现“正面朝上” 的频数是4,频率为 ;
出现“反面朝上”的频数是6,频率为
可以发现,“正面朝上” 和“反面朝上” 的频数之和为试验总次数;而这两种情况的频率之和为1. 一般地,如果重复进行n次试验,某个试验结果
出现的次数m 称为这个试验结果在这n次实验中出现的频数,而频数与试验总次数的比 称为这个试验结果在这n次试验中出现的频率. 一次掷两枚硬币,用A,B,C分别代表可能发生的三种情形: A. 两枚硬币都是“正面朝上”; B. 两枚硬币都是“反面朝上”; C. 一枚硬币“正面朝上”,另一枚硬币“反面朝上”. 每次掷币都发生A,B,C三种情形中的一种,并且只发生一种. A,B,C发生的频数与频率 现在全班同学每人各掷两枚硬币5 次,记录所得结果, 将全班的结果汇总填入下表中,并计算频率.说一说,出现哪一种情形的频率高? 全班每组同学抛掷一枚硬币40 次,记录出现“正面朝上”
的结果,将各组试验结果汇总,完成下表:根据上表, 在下图中绘制“正面朝上” 的频率变化折线统计图.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
