第一单元 长方体和正方体(单元测试)-2024-2025学年六年级上册数学苏教版(含答案)
文档属性
| 名称 | 第一单元 长方体和正方体(单元测试)-2024-2025学年六年级上册数学苏教版(含答案) | 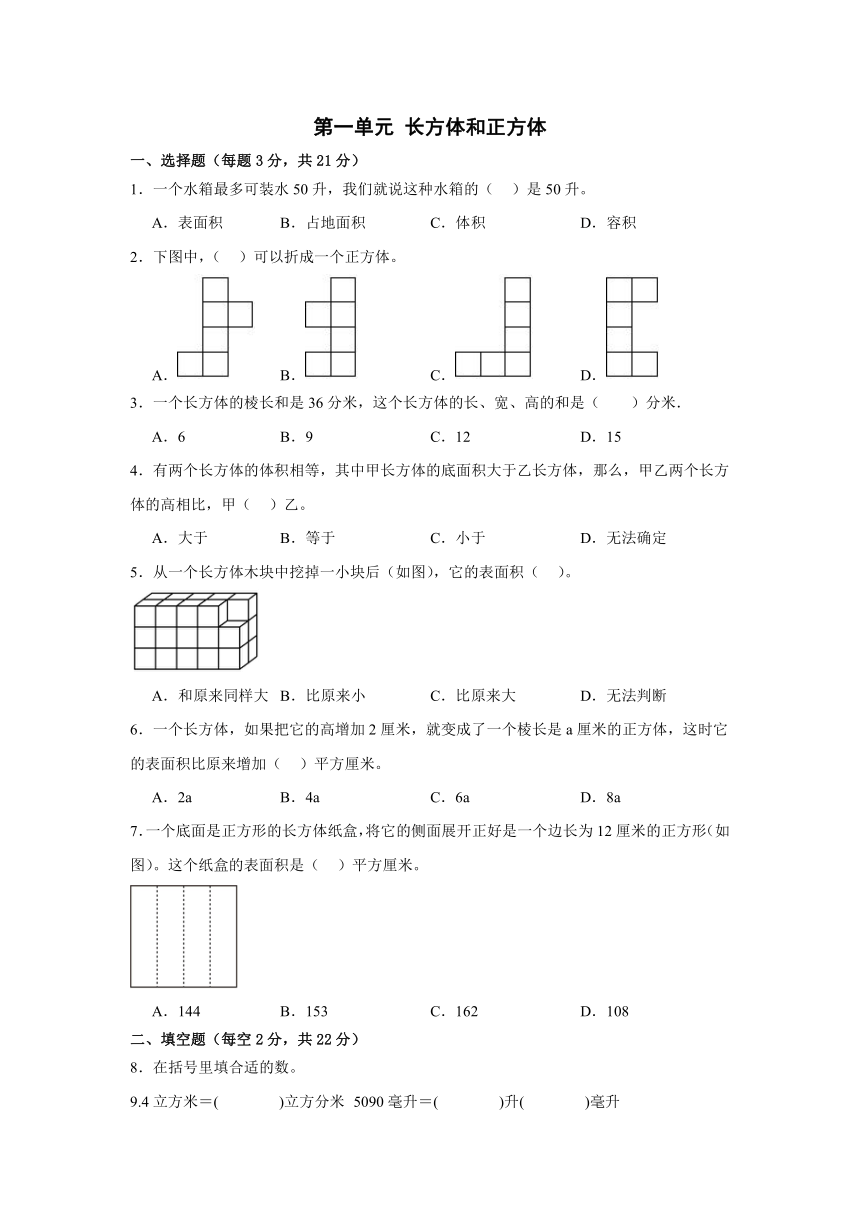 | |
| 格式 | docx | ||
| 文件大小 | 125.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-23 10:53:11 | ||
图片预览

文档简介
第一单元 长方体和正方体
一、选择题(每题3分,共21分)
1.一个水箱最多可装水50升,我们就说这种水箱的( )是50升。
A.表面积 B.占地面积 C.体积 D.容积
2.下图中,( )可以折成一个正方体。
A. B. C. D.
3.一个长方体的棱长和是36分米,这个长方体的长、宽、高的和是( )分米.
A.6 B.9 C.12 D.15
4.有两个长方体的体积相等,其中甲长方体的底面积大于乙长方体,那么,甲乙两个长方体的高相比,甲( )乙。
A.大于 B.等于 C.小于 D.无法确定
5.从一个长方体木块中挖掉一小块后(如图),它的表面积( )。
A.和原来同样大 B.比原来小 C.比原来大 D.无法判断
6.一个长方体,如果把它的高增加2厘米,就变成了一个棱长是a厘米的正方体,这时它的表面积比原来增加( )平方厘米。
A.2a B.4a C.6a D.8a
7.一个底面是正方形的长方体纸盒,将它的侧面展开正好是一个边长为12厘米的正方形(如图)。这个纸盒的表面积是( )平方厘米。
A.144 B.153 C.162 D.108
二、填空题(每空2分,共22分)
8.在括号里填合适的数。
9.4立方米=( )立方分米 5090毫升=( )升( )毫升
8升=( )立方厘米 3.5升=( )升( )毫升
9.在括号里填上合适的单位名称。
一个5G手机的体积大约是85( ),一个眼药水瓶的容积大约是10( )。
10.一个长方体的高减少3厘米,就变成了一个正方体,表面积比原来减少60平方厘米,原来长方体的体积是( )立方厘米.
11.一个棱长1分米的正方体锯成两个大小不同的长方体,大长方体的表面积比小长方体大200平方厘米,小长方体的表面积是( )平方厘米。
12.有6根4分米,10根5分米的细铁条,用其中的12根铁条焊接成一个长方体框架(铁条不折断,接头处忽略不计),要给这个长方体框架蒙上一层包装纸,至少需要( )平方分米的纸。
13.如图,一张长方形铁皮,利用图中的阴影部分刚好能做成一个长是8厘米、宽是5厘米、高是2厘米的长方体盒子,这张长方形铁皮的面积是( )平方厘米。
三、判断题(每题2分,共10分)
14.一个长方体其长不变,宽变为原来的2倍,高变为原来的3倍,则其表面积和体积都变为原来的6倍。( )
15.一个长方体中,相邻的两个面可以是正方形。 ( )
16.正方体相对面的面积相等,所有相邻面的面积也都相等。( )
17.一个正方体的棱长为a米,把它切成两个小长方体后,表面积之和为8a2平方米. ( )
18.把一块橡皮泥捏成泥人或正方体,它们的体积一样大。( )
四、计算题(8分)
19.求下面各立方体的表面积和体积。(单位:厘米)
五、解答题(共39分)
20.光明小学准备修建一个长6米、宽3米、深50厘米的沙坑。
(1)如果要在沙坑的四周和底面抹上水泥,抹水泥的面积是多少平方米?
(2)如果要在沙坑里填满黄沙,准备黄沙19吨,够不够?(每立方米黄沙重2.4吨)
21.少年宫门前共有3级台阶,每级台阶长10米,宽0.5米,高0.3米。
(1)3级台阶共占地多少平方米?
(2)给3级台阶都铺上大理石,需大理石多少平方米?
22.明明准备把送给小刚的飞机模型装进一个长方体的包装盒里,这个包装盒的长、宽、高分别是15cm、8cm、10cm.装好后用彩带把这个包装盒捆上(如图所示),接头处彩带长18cm.一共需要多少厘米彩带?
23.找一个长方体火柴盒,测量有关数据,算出它的内盒和外盒至少各用硬纸多少平方厘米。(接头处忽略不计)
24.张明在一个长8厘米,宽8厘米,高12厘米的长方体容器中加入一些水后,准备测量一块石头的体积,具体情况如下图所示,请问这个石头的体积是多少?
25.将一个横截面是正方形的长方体平均截成2段,每段长3厘米,表面积增加了32平方厘米,这个长方体原来的表面积是多少?
26.如图所示用绳子捆扎一种礼品盒,如果结头处的绳长为12厘米,一根10米长的绳子最多可以捆几盒?还剩多少厘米?
参考答案:
1.D
2.A
3.B
4.C
5.A
6.D
7.C
8. 9400 5 90 8000 3 500
9. 立方厘米 毫升
10.200
11.300
12.130
13.180
14.×
15.×
16.√
17.
18.√
19.长方体:312平方厘米;360立方厘米。
正方体:150平方厘米;125立方厘米。
20.(1)27平方米;(2)不够
21.(1)15平方米(2)24平方米
22.104厘米
23.内盒32.78平方厘米;外盒43.2平方厘米
24.128立方厘米
25.128平方厘米
26.6盒,88厘米
一、选择题(每题3分,共21分)
1.一个水箱最多可装水50升,我们就说这种水箱的( )是50升。
A.表面积 B.占地面积 C.体积 D.容积
2.下图中,( )可以折成一个正方体。
A. B. C. D.
3.一个长方体的棱长和是36分米,这个长方体的长、宽、高的和是( )分米.
A.6 B.9 C.12 D.15
4.有两个长方体的体积相等,其中甲长方体的底面积大于乙长方体,那么,甲乙两个长方体的高相比,甲( )乙。
A.大于 B.等于 C.小于 D.无法确定
5.从一个长方体木块中挖掉一小块后(如图),它的表面积( )。
A.和原来同样大 B.比原来小 C.比原来大 D.无法判断
6.一个长方体,如果把它的高增加2厘米,就变成了一个棱长是a厘米的正方体,这时它的表面积比原来增加( )平方厘米。
A.2a B.4a C.6a D.8a
7.一个底面是正方形的长方体纸盒,将它的侧面展开正好是一个边长为12厘米的正方形(如图)。这个纸盒的表面积是( )平方厘米。
A.144 B.153 C.162 D.108
二、填空题(每空2分,共22分)
8.在括号里填合适的数。
9.4立方米=( )立方分米 5090毫升=( )升( )毫升
8升=( )立方厘米 3.5升=( )升( )毫升
9.在括号里填上合适的单位名称。
一个5G手机的体积大约是85( ),一个眼药水瓶的容积大约是10( )。
10.一个长方体的高减少3厘米,就变成了一个正方体,表面积比原来减少60平方厘米,原来长方体的体积是( )立方厘米.
11.一个棱长1分米的正方体锯成两个大小不同的长方体,大长方体的表面积比小长方体大200平方厘米,小长方体的表面积是( )平方厘米。
12.有6根4分米,10根5分米的细铁条,用其中的12根铁条焊接成一个长方体框架(铁条不折断,接头处忽略不计),要给这个长方体框架蒙上一层包装纸,至少需要( )平方分米的纸。
13.如图,一张长方形铁皮,利用图中的阴影部分刚好能做成一个长是8厘米、宽是5厘米、高是2厘米的长方体盒子,这张长方形铁皮的面积是( )平方厘米。
三、判断题(每题2分,共10分)
14.一个长方体其长不变,宽变为原来的2倍,高变为原来的3倍,则其表面积和体积都变为原来的6倍。( )
15.一个长方体中,相邻的两个面可以是正方形。 ( )
16.正方体相对面的面积相等,所有相邻面的面积也都相等。( )
17.一个正方体的棱长为a米,把它切成两个小长方体后,表面积之和为8a2平方米. ( )
18.把一块橡皮泥捏成泥人或正方体,它们的体积一样大。( )
四、计算题(8分)
19.求下面各立方体的表面积和体积。(单位:厘米)
五、解答题(共39分)
20.光明小学准备修建一个长6米、宽3米、深50厘米的沙坑。
(1)如果要在沙坑的四周和底面抹上水泥,抹水泥的面积是多少平方米?
(2)如果要在沙坑里填满黄沙,准备黄沙19吨,够不够?(每立方米黄沙重2.4吨)
21.少年宫门前共有3级台阶,每级台阶长10米,宽0.5米,高0.3米。
(1)3级台阶共占地多少平方米?
(2)给3级台阶都铺上大理石,需大理石多少平方米?
22.明明准备把送给小刚的飞机模型装进一个长方体的包装盒里,这个包装盒的长、宽、高分别是15cm、8cm、10cm.装好后用彩带把这个包装盒捆上(如图所示),接头处彩带长18cm.一共需要多少厘米彩带?
23.找一个长方体火柴盒,测量有关数据,算出它的内盒和外盒至少各用硬纸多少平方厘米。(接头处忽略不计)
24.张明在一个长8厘米,宽8厘米,高12厘米的长方体容器中加入一些水后,准备测量一块石头的体积,具体情况如下图所示,请问这个石头的体积是多少?
25.将一个横截面是正方形的长方体平均截成2段,每段长3厘米,表面积增加了32平方厘米,这个长方体原来的表面积是多少?
26.如图所示用绳子捆扎一种礼品盒,如果结头处的绳长为12厘米,一根10米长的绳子最多可以捆几盒?还剩多少厘米?
参考答案:
1.D
2.A
3.B
4.C
5.A
6.D
7.C
8. 9400 5 90 8000 3 500
9. 立方厘米 毫升
10.200
11.300
12.130
13.180
14.×
15.×
16.√
17.
18.√
19.长方体:312平方厘米;360立方厘米。
正方体:150平方厘米;125立方厘米。
20.(1)27平方米;(2)不够
21.(1)15平方米(2)24平方米
22.104厘米
23.内盒32.78平方厘米;外盒43.2平方厘米
24.128立方厘米
25.128平方厘米
26.6盒,88厘米
