苏科版八年级数学上册试题第6章《 一次函数》 章节检测卷(含详解)
文档属性
| 名称 | 苏科版八年级数学上册试题第6章《 一次函数》 章节检测卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 553.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-23 11:39:52 | ||
图片预览



文档简介
第6章《 一次函数》 章节检测卷
一.选择题(每小题2分,共12分)
1.下列图象中,表示y不是x的函数的是( )
A. B. C. D.
2.当k<0时,一次函数y=kx﹣k的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知某一次函数的图象与直线y=-3x平行,且与函数y=3x+5的图象交y轴上于同一点,那么这个一次函数的解析式是( )
A.y=3x+5 B.y=3x-5
C.y=-3x+5 D.y=-3x-5
4.如图,函数 y1=﹣2x 与 y2=ax+3 的图象相交于点 A(m,2),则关于 x 的不等式﹣2x>ax+3 的解集是( )
A.x>2 B.x<2 C.x>﹣1 D.x<﹣1
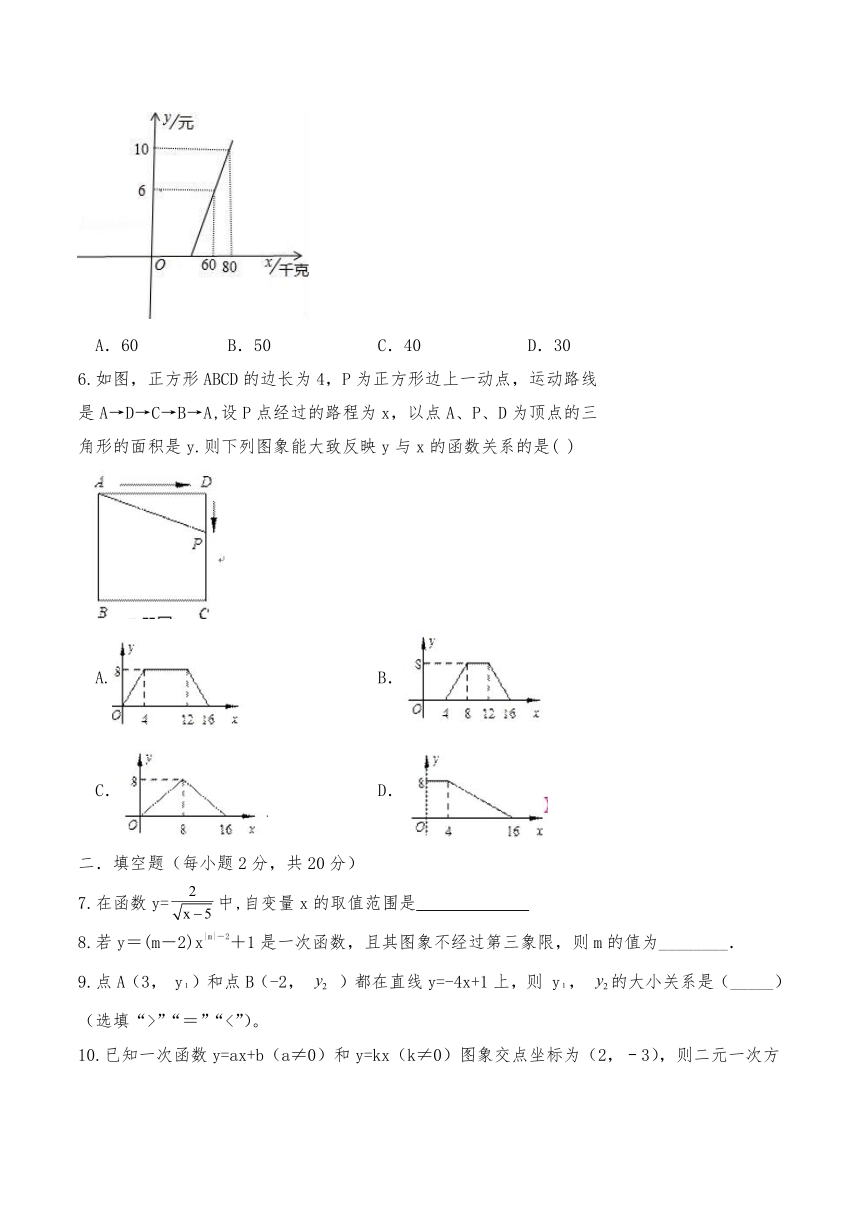
5.某长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规定的质量,则需购买行李票,行李费用y(元)是行李质量x(千克)的一次函数,其图象如图所示.旅客最多可免费携带的行李质量是( )千克.
A.60 B.50 C.40 D.30
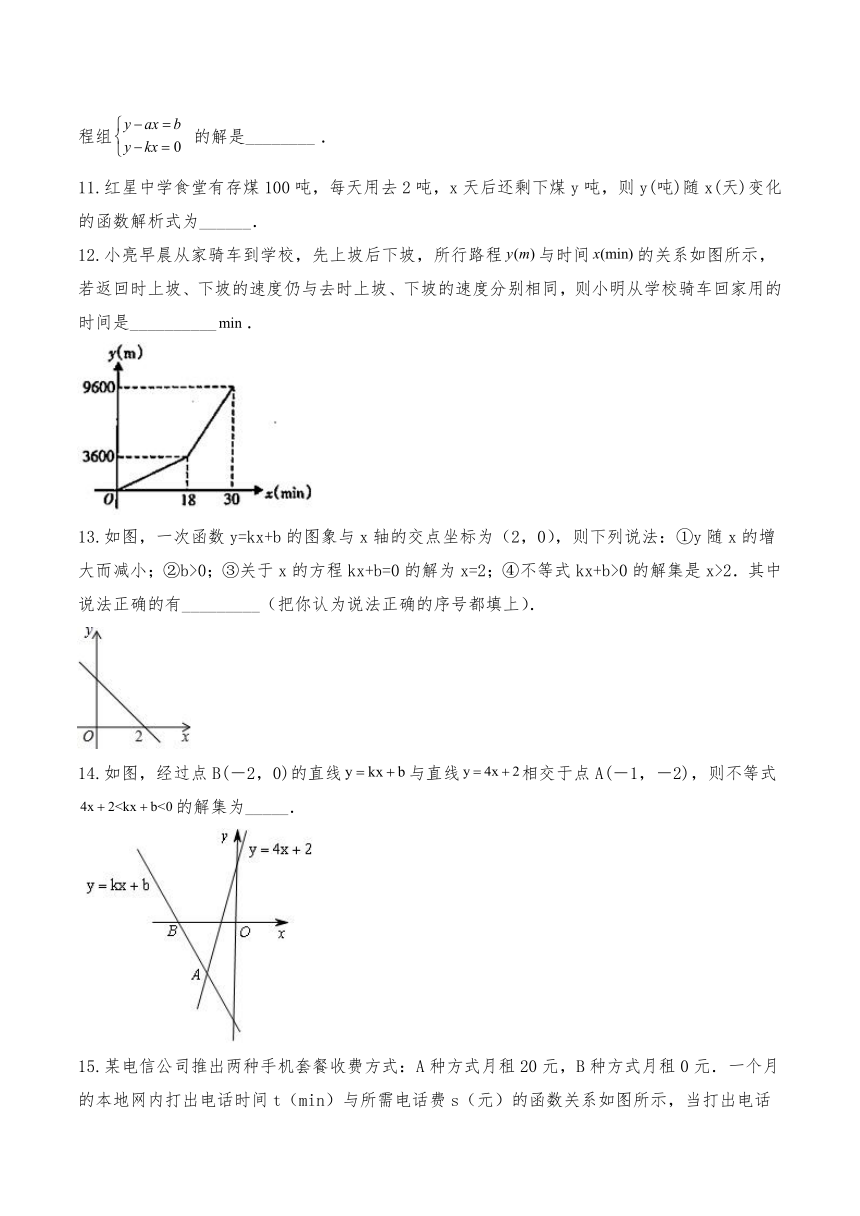
6.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线
是A→D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三
角形的面积是y.则下列图象能大致反映y与x的函数关系的是( )
A. B.
C. D.
二.填空题(每小题2分,共20分)
7.在函数y=中,自变量x的取值范围是
8.若y=(m-2)x|m|-2+1是一次函数,且其图象不经过第三象限,则m的值为________.
9.点A(3, y)和点B(-2, )都在直线y=-4x+1上,则 y, 的大小关系是(_____) (选填“>”“=”“<”)。
10.已知一次函数y=ax+b(a≠0)和y=kx(k≠0)图象交点坐标为(2,﹣3),则二元一次方程组 的解是________ .
11.红星中学食堂有存煤100吨,每天用去2吨,x天后还剩下煤y吨,则y(吨)随x(天)变化的函数解析式为______.
12.小亮早晨从家骑车到学校,先上坡后下坡,所行路程与时间的关系如图所示,若返回时上坡、下坡的速度仍与去时上坡、下坡的速度分别相同,则小明从学校骑车回家用的时间是__________.
13.如图,一次函数y=kx+b的图象与x轴的交点坐标为(2,0),则下列说法:①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2;④不等式kx+b>0的解集是x>2.其中说法正确的有_________(把你认为说法正确的序号都填上).
14.如图,经过点B(-2,0)的直线与直线相交于点A(-1,-2),则不等式的解集为_____.
15.某电信公司推出两种手机套餐收费方式:A种方式月租20元,B种方式月租0元.一个月的本地网内打出电话时间t(min)与所需电话费s(元)的函数关系如图所示,当打出电话150min时,这两种收费方式的电话费相差________元.
16.正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3…和点C1,C2,C3…分别在直线y=x+1和x轴上,则点Bn的坐标为_____.(n为正整数)
三.解答题(共68分)
17.(8分)已知函数y=(m+1)x2-|m|+n+4.
(1)当m,n为何值时,此函数是一次函数?
(2)当m,n为何值时,此函数是正比例函数?
18.(10分)已知一次函数的图象经过A(-2,-3),B(1,3)两点.
(1)求这个一次函数的解析式;
(2)试判断点P(-1,1)是否在这个一次函数的图象上;
(3)求此函数与x轴、y轴围成的三角形的面积.
19.(10分)20.(10分)已知与成正比例,且当时,.
(1)写出与之间的函数表达式;
(2)当时,求的值;
(3)若y的取值范围为,求的取值范围.
20.(10分)为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式.下图描述了两种方式应支付金额(元)与骑行时间(时)之间的函数关系.根据图象回答下列问题.
(1)求手机支付金额(元)与骑行时间(时)的函数关系式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.
21.(10分)甲、乙两车同时从A、B两地相向而行,设两车行驶的时间为x(h),与A地的距离为y(km),y(km)与x(h)关系如图所示:
(1)直接写出y甲和y乙的关系式;
(2)甲、乙两车几小时相遇?
(3)当两车距离为100千米时,甲车行驶了多长时间?
(4)当乙车到达A地后立刻按原速度返回,乙能否在甲到达B地前追上甲.
22.(10分)已知动点P以每秒2 cm的速度沿图(1)的边框按从B C D E F A的路径移动,相应的△ABP的面积S与时间t之间的关系如图(2)中的图象表示.若AB=6 cm,试回答下列问题:
(1)图(1)中的BC长是多少
(2)图(2)中的a是多少
(3)图(1)中的图形面积是多少
(4)图(2)中的b是多少
23.(10分)在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长的数值与面积的数值相等,则这个点叫做和谐点.例如,图中过点分别作轴,轴的垂线.与坐标轴围成矩形的周长的数值与面积的数值相等,则点是和谐点.
(1)判断点,是否为和谐点,并说明理由;
(2)若和谐点在直线(为常数)上,求的值.
答案
一.选择题
1.B
【解析】选项B中,当x>0时对每个x值都有两个y值与之对应,不满足函数定义中的“唯一性”,而选项A、C、D对每个x值都有唯一y值与之对应.
故选B.
2.C
【解析】∵k<0,∴﹣k>0,∴一次函数y=kx﹣k的图象经过第一、二、四象限.故选C.
3.C
【解析】解:∵函数y=3x+5的图象交y轴于(0,5),
∴设函数解析式为y=-3x+k,代入(0,5)得,k=5,
∴一次函数的解析式是y=-3x+5
故选C.
4.D
【解析】因为函数与的图象相交于点A(m,2),把点A代入可求出,所以点A(-1,2),然后把点A代入解得, 不等式,
可化为,解不等式可得:,故选D.
5.D
【解析】解:设一次函数y=kx+b,
∵当x=60时,y=6,当x=80时,y=10,
∴ 解得
∴所求函数关系式为y=x-6(x≥30);
当y=0时,x-6=0,所以x=30,
故旅客最多可免费携带30kg行李.
故选D.
6.B
【解析】通过几个特殊点就大致知道图像了,P点在AD段时面积为零,在DC段先升,在CB段因为底和高不变所以面积不变,在BA段下降,故选B
二.填空题
7.x>5
【解析】由题意得x-5≥0,且x-5≠0,∴x>5
8.-3
【解析】解:∵y=(m-2)x|m|-2+1是一次函数,图象不经过第三象限,
∴且|m|-2=1,解得:m,m=,∴m=-3.
9.<.
【解析】∵直线y=-4x+1,∴y随x的增大而减小,
又∵点A(3, y)和点B(-2, )都在直线y=-4x+1上,3〉-2,
∴y110.
【解析】因为函数图象交点坐标为两函数解析式组成的方程组的解,
所以二元一次方程组 的解是.
故答案为:.
11.y=100-2x
【解析】由题意得,y=100-2x,
则y(吨)随x(天)变化的函数解析式为y=100-2x,
故答案为:y=100-2x.
12.37.2
【解析】由图可得,去校时,上坡路的距离为2000米,所用时间为18分,
∴上坡速度=3600÷18=200米/分,
下坡路的距离是9600-3600=6000米,所用时间为30-18=12分,
∴下坡速度=6000÷ 12=500米/分;
∵去学校时的上坡回家时变为下坡、去学校时的下坡回家时变为上坡,
∴小明从学校骑车回家用的时间是:6000÷+3600÷500=30+7.2=37.2分钟.
故答案为37.2.
13.①②③
【解析】①因为一次函数的图象经过二、四象限,所以y随x的增大而减小,故本项正确;
②因为一次函数的图象与y轴的交点在正半轴上,所以b>0,故本项正确;
③因为一次函数的图象与x轴的交点为(2,0),所以当y=0时,x=2,即关于x的方程kx+b=0的解为x=2,故本项正确;
④由图象可得不等式kx+b>0的解集是x<2,故本项是错误的.故正确的有①②③.
14.
【解析】不等式的解集就是在x下方,直线在直线上方时x的取值范围.
由图象可知,此时.
15.10
【解析】解:解法1:由题图可知,当打出电话100min时,所需电话费相同.
可设A种方式打电话每分钟付费x元,B种方式打电话每分钟付费y元,则,整理得,
所以打出电话150min时,两种收费方式的电话费相差(元).
解法2:设A种方式对应的函数解析式为y=k1t+20,B种方式对应的函数解析式为y=k2t,
当t=100时,100k1+20=100k2,∴k2-k1=,
当t=150时,150k2-150k1-20=150×-20=10.
16.(2n﹣1,2n﹣1)
【解析】∵直线y=x+1,当x=0时,y=1,当y=0时,x=-1,
∴OA1=1,∴B1(1,1),
∵OA1=1,OD=1,∴∠ODA1=45°,∴∠A2A1B1=45°,∴A2B1=A1B1=1,∴A2C1=2=21,∴B2(3,2),
同理得:A3C2=4=22,…,
∴B3(23-1,23-1),∴Bn(2n 1,2n 1),
故答案为Bn(2n 1,2n 1).
三.解答题
17.(1)根据一次函数的定义,得:2 |m|=1,解得:m=±1.
又∵m+1≠0即m≠ 1,
∴当m=1,n为任意实数时,这个函数是一次函数;
(2)根据正比例函数的定义,得:2 |m|=1,n+4=0,解得:m=±1,n= 4,
又∵m+1≠0即m≠ 1,
∴当m=1,n= 4时,这个函数是正比例函数.
18.(1)设一次函数的表达式为y=kx+b,
则-3=-2k+b、3=k+b,解得:k=2,b=1.
∴函数的解析式为:y=2x+1.
(2)将点P(-1,1)代入函数解析式,1≠-2+1,
∴点P不在这个一次函数的图象上.
(3)当x=0,y=1,当y=0,x=,
此函数与x轴、y轴围成的三角形的面积为:
19.(1)∵y+3与x+2成正比例,
∴可设y+3=k(x+2),
把x=3时,y=7代入得:7+3=k(3+2),解得k=2,
故y+3=2(x+2),
故y与x之间的函数关系式为y=2x+1;
(2)把x= 1代入(1)中所求函数关系式得,y=2x+1= 2+1= 1,
(3)当时, 解得:
20.(1)手机支付金额与骑行时间之间的函数关系式为;
(2)设会员卡支付金额与骑行时间之间的函数关系式为,由题意可得,,
∴使用会员卡支付金额与骑行时间之间的函数关系式为,
由,得,
∴当骑行时间大于2小时时,使用会员卡支付比较合算;当骑行时间等于2小时时,使用手机支付和会员卡支付均可;当骑行时间小于2小时时,使用手机支付比较合算.
21.(1)y甲=60x,y乙=﹣100x+300;
(2)根据题意得:﹣100x+300=60x,解得:x=,
答:甲、乙两车小时相遇;
(3)根据题意得:
①y甲﹣y乙=100,即60x﹣(﹣100x+300)=100,解得:x=;
②y乙﹣y甲=100,即﹣100x+300﹣60x=100,解得:x=;
答:当两车距离为100千米时,甲车行驶了小时或小时.
(4)根据题意得:100x﹣300=60x,解得:x=7.5,
∵7.5>5,∴乙不能在甲到达B地前追上甲.
22.(1)由图象知,当t由0增大到4时,点P由B C,∴BC==4×2=8(㎝) ;
(2) a=S△ABC=×6×8=24(㎝2) ;
(3) 同理,由图象知 CD=4㎝,DE=6㎝,则EF=2㎝,AF=14㎝
∴图1中的图象面积为6×14-4×6=60㎝2 ;
(4) 图1中的多边形的周长为(14+6)×2=40㎝ b=(40-6)÷2=17秒.
23.解:(1)∵,∴点M不是和谐点,点N是和谐点;
(2)∵点P是和谐点,∴,解得,∴点P的坐标为
∵点P在直线上,∴代入得,解得
∴的值分别是6,9.
一.选择题(每小题2分,共12分)
1.下列图象中,表示y不是x的函数的是( )
A. B. C. D.
2.当k<0时,一次函数y=kx﹣k的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知某一次函数的图象与直线y=-3x平行,且与函数y=3x+5的图象交y轴上于同一点,那么这个一次函数的解析式是( )
A.y=3x+5 B.y=3x-5
C.y=-3x+5 D.y=-3x-5
4.如图,函数 y1=﹣2x 与 y2=ax+3 的图象相交于点 A(m,2),则关于 x 的不等式﹣2x>ax+3 的解集是( )
A.x>2 B.x<2 C.x>﹣1 D.x<﹣1
5.某长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规定的质量,则需购买行李票,行李费用y(元)是行李质量x(千克)的一次函数,其图象如图所示.旅客最多可免费携带的行李质量是( )千克.
A.60 B.50 C.40 D.30
6.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线
是A→D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三
角形的面积是y.则下列图象能大致反映y与x的函数关系的是( )
A. B.
C. D.
二.填空题(每小题2分,共20分)
7.在函数y=中,自变量x的取值范围是
8.若y=(m-2)x|m|-2+1是一次函数,且其图象不经过第三象限,则m的值为________.
9.点A(3, y)和点B(-2, )都在直线y=-4x+1上,则 y, 的大小关系是(_____) (选填“>”“=”“<”)。
10.已知一次函数y=ax+b(a≠0)和y=kx(k≠0)图象交点坐标为(2,﹣3),则二元一次方程组 的解是________ .
11.红星中学食堂有存煤100吨,每天用去2吨,x天后还剩下煤y吨,则y(吨)随x(天)变化的函数解析式为______.
12.小亮早晨从家骑车到学校,先上坡后下坡,所行路程与时间的关系如图所示,若返回时上坡、下坡的速度仍与去时上坡、下坡的速度分别相同,则小明从学校骑车回家用的时间是__________.
13.如图,一次函数y=kx+b的图象与x轴的交点坐标为(2,0),则下列说法:①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2;④不等式kx+b>0的解集是x>2.其中说法正确的有_________(把你认为说法正确的序号都填上).
14.如图,经过点B(-2,0)的直线与直线相交于点A(-1,-2),则不等式的解集为_____.
15.某电信公司推出两种手机套餐收费方式:A种方式月租20元,B种方式月租0元.一个月的本地网内打出电话时间t(min)与所需电话费s(元)的函数关系如图所示,当打出电话150min时,这两种收费方式的电话费相差________元.
16.正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3…和点C1,C2,C3…分别在直线y=x+1和x轴上,则点Bn的坐标为_____.(n为正整数)
三.解答题(共68分)
17.(8分)已知函数y=(m+1)x2-|m|+n+4.
(1)当m,n为何值时,此函数是一次函数?
(2)当m,n为何值时,此函数是正比例函数?
18.(10分)已知一次函数的图象经过A(-2,-3),B(1,3)两点.
(1)求这个一次函数的解析式;
(2)试判断点P(-1,1)是否在这个一次函数的图象上;
(3)求此函数与x轴、y轴围成的三角形的面积.
19.(10分)20.(10分)已知与成正比例,且当时,.
(1)写出与之间的函数表达式;
(2)当时,求的值;
(3)若y的取值范围为,求的取值范围.
20.(10分)为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式.下图描述了两种方式应支付金额(元)与骑行时间(时)之间的函数关系.根据图象回答下列问题.
(1)求手机支付金额(元)与骑行时间(时)的函数关系式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.
21.(10分)甲、乙两车同时从A、B两地相向而行,设两车行驶的时间为x(h),与A地的距离为y(km),y(km)与x(h)关系如图所示:
(1)直接写出y甲和y乙的关系式;
(2)甲、乙两车几小时相遇?
(3)当两车距离为100千米时,甲车行驶了多长时间?
(4)当乙车到达A地后立刻按原速度返回,乙能否在甲到达B地前追上甲.
22.(10分)已知动点P以每秒2 cm的速度沿图(1)的边框按从B C D E F A的路径移动,相应的△ABP的面积S与时间t之间的关系如图(2)中的图象表示.若AB=6 cm,试回答下列问题:
(1)图(1)中的BC长是多少
(2)图(2)中的a是多少
(3)图(1)中的图形面积是多少
(4)图(2)中的b是多少
23.(10分)在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长的数值与面积的数值相等,则这个点叫做和谐点.例如,图中过点分别作轴,轴的垂线.与坐标轴围成矩形的周长的数值与面积的数值相等,则点是和谐点.
(1)判断点,是否为和谐点,并说明理由;
(2)若和谐点在直线(为常数)上,求的值.
答案
一.选择题
1.B
【解析】选项B中,当x>0时对每个x值都有两个y值与之对应,不满足函数定义中的“唯一性”,而选项A、C、D对每个x值都有唯一y值与之对应.
故选B.
2.C
【解析】∵k<0,∴﹣k>0,∴一次函数y=kx﹣k的图象经过第一、二、四象限.故选C.
3.C
【解析】解:∵函数y=3x+5的图象交y轴于(0,5),
∴设函数解析式为y=-3x+k,代入(0,5)得,k=5,
∴一次函数的解析式是y=-3x+5
故选C.
4.D
【解析】因为函数与的图象相交于点A(m,2),把点A代入可求出,所以点A(-1,2),然后把点A代入解得, 不等式,
可化为,解不等式可得:,故选D.
5.D
【解析】解:设一次函数y=kx+b,
∵当x=60时,y=6,当x=80时,y=10,
∴ 解得
∴所求函数关系式为y=x-6(x≥30);
当y=0时,x-6=0,所以x=30,
故旅客最多可免费携带30kg行李.
故选D.
6.B
【解析】通过几个特殊点就大致知道图像了,P点在AD段时面积为零,在DC段先升,在CB段因为底和高不变所以面积不变,在BA段下降,故选B
二.填空题
7.x>5
【解析】由题意得x-5≥0,且x-5≠0,∴x>5
8.-3
【解析】解:∵y=(m-2)x|m|-2+1是一次函数,图象不经过第三象限,
∴且|m|-2=1,解得:m,m=,∴m=-3.
9.<.
【解析】∵直线y=-4x+1,∴y随x的增大而减小,
又∵点A(3, y)和点B(-2, )都在直线y=-4x+1上,3〉-2,
∴y1
【解析】因为函数图象交点坐标为两函数解析式组成的方程组的解,
所以二元一次方程组 的解是.
故答案为:.
11.y=100-2x
【解析】由题意得,y=100-2x,
则y(吨)随x(天)变化的函数解析式为y=100-2x,
故答案为:y=100-2x.
12.37.2
【解析】由图可得,去校时,上坡路的距离为2000米,所用时间为18分,
∴上坡速度=3600÷18=200米/分,
下坡路的距离是9600-3600=6000米,所用时间为30-18=12分,
∴下坡速度=6000÷ 12=500米/分;
∵去学校时的上坡回家时变为下坡、去学校时的下坡回家时变为上坡,
∴小明从学校骑车回家用的时间是:6000÷+3600÷500=30+7.2=37.2分钟.
故答案为37.2.
13.①②③
【解析】①因为一次函数的图象经过二、四象限,所以y随x的增大而减小,故本项正确;
②因为一次函数的图象与y轴的交点在正半轴上,所以b>0,故本项正确;
③因为一次函数的图象与x轴的交点为(2,0),所以当y=0时,x=2,即关于x的方程kx+b=0的解为x=2,故本项正确;
④由图象可得不等式kx+b>0的解集是x<2,故本项是错误的.故正确的有①②③.
14.
【解析】不等式的解集就是在x下方,直线在直线上方时x的取值范围.
由图象可知,此时.
15.10
【解析】解:解法1:由题图可知,当打出电话100min时,所需电话费相同.
可设A种方式打电话每分钟付费x元,B种方式打电话每分钟付费y元,则,整理得,
所以打出电话150min时,两种收费方式的电话费相差(元).
解法2:设A种方式对应的函数解析式为y=k1t+20,B种方式对应的函数解析式为y=k2t,
当t=100时,100k1+20=100k2,∴k2-k1=,
当t=150时,150k2-150k1-20=150×-20=10.
16.(2n﹣1,2n﹣1)
【解析】∵直线y=x+1,当x=0时,y=1,当y=0时,x=-1,
∴OA1=1,∴B1(1,1),
∵OA1=1,OD=1,∴∠ODA1=45°,∴∠A2A1B1=45°,∴A2B1=A1B1=1,∴A2C1=2=21,∴B2(3,2),
同理得:A3C2=4=22,…,
∴B3(23-1,23-1),∴Bn(2n 1,2n 1),
故答案为Bn(2n 1,2n 1).
三.解答题
17.(1)根据一次函数的定义,得:2 |m|=1,解得:m=±1.
又∵m+1≠0即m≠ 1,
∴当m=1,n为任意实数时,这个函数是一次函数;
(2)根据正比例函数的定义,得:2 |m|=1,n+4=0,解得:m=±1,n= 4,
又∵m+1≠0即m≠ 1,
∴当m=1,n= 4时,这个函数是正比例函数.
18.(1)设一次函数的表达式为y=kx+b,
则-3=-2k+b、3=k+b,解得:k=2,b=1.
∴函数的解析式为:y=2x+1.
(2)将点P(-1,1)代入函数解析式,1≠-2+1,
∴点P不在这个一次函数的图象上.
(3)当x=0,y=1,当y=0,x=,
此函数与x轴、y轴围成的三角形的面积为:
19.(1)∵y+3与x+2成正比例,
∴可设y+3=k(x+2),
把x=3时,y=7代入得:7+3=k(3+2),解得k=2,
故y+3=2(x+2),
故y与x之间的函数关系式为y=2x+1;
(2)把x= 1代入(1)中所求函数关系式得,y=2x+1= 2+1= 1,
(3)当时, 解得:
20.(1)手机支付金额与骑行时间之间的函数关系式为;
(2)设会员卡支付金额与骑行时间之间的函数关系式为,由题意可得,,
∴使用会员卡支付金额与骑行时间之间的函数关系式为,
由,得,
∴当骑行时间大于2小时时,使用会员卡支付比较合算;当骑行时间等于2小时时,使用手机支付和会员卡支付均可;当骑行时间小于2小时时,使用手机支付比较合算.
21.(1)y甲=60x,y乙=﹣100x+300;
(2)根据题意得:﹣100x+300=60x,解得:x=,
答:甲、乙两车小时相遇;
(3)根据题意得:
①y甲﹣y乙=100,即60x﹣(﹣100x+300)=100,解得:x=;
②y乙﹣y甲=100,即﹣100x+300﹣60x=100,解得:x=;
答:当两车距离为100千米时,甲车行驶了小时或小时.
(4)根据题意得:100x﹣300=60x,解得:x=7.5,
∵7.5>5,∴乙不能在甲到达B地前追上甲.
22.(1)由图象知,当t由0增大到4时,点P由B C,∴BC==4×2=8(㎝) ;
(2) a=S△ABC=×6×8=24(㎝2) ;
(3) 同理,由图象知 CD=4㎝,DE=6㎝,则EF=2㎝,AF=14㎝
∴图1中的图象面积为6×14-4×6=60㎝2 ;
(4) 图1中的多边形的周长为(14+6)×2=40㎝ b=(40-6)÷2=17秒.
23.解:(1)∵,∴点M不是和谐点,点N是和谐点;
(2)∵点P是和谐点,∴,解得,∴点P的坐标为
∵点P在直线上,∴代入得,解得
∴的值分别是6,9.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
