1.5y=Asin(ωx+ψ)的图像
文档属性
| 名称 | 1.5y=Asin(ωx+ψ)的图像 |  | |
| 格式 | zip | ||
| 文件大小 | 704.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-31 21:18:50 | ||
图片预览





文档简介
课件43张PPT。洗拖把其中A, ω, φ都是常数在y=sinx中
A=_______, ω=______
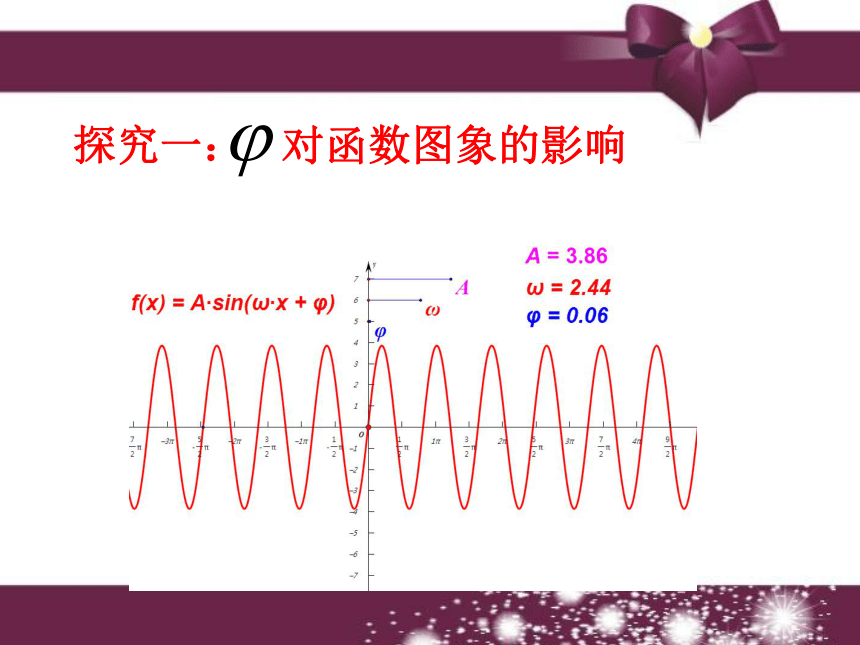
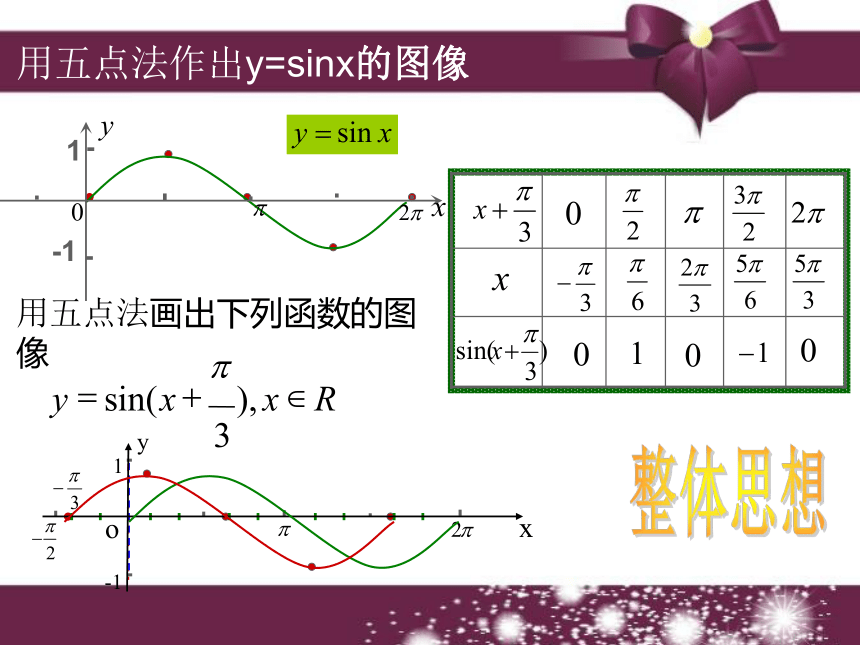
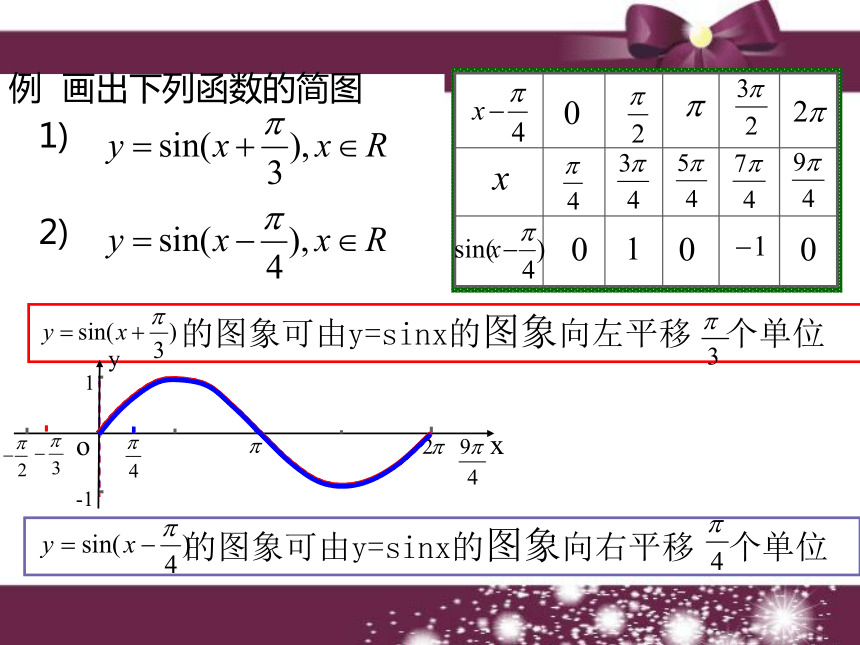
φ=_______1101.5 函数 的图象探究一: 对函数图象的影响用五点法作出y=sinx的图像整体思想 的图象可由y=sinx的图象向左平移 个单位例? 画出下列函数的简图
1)
2)
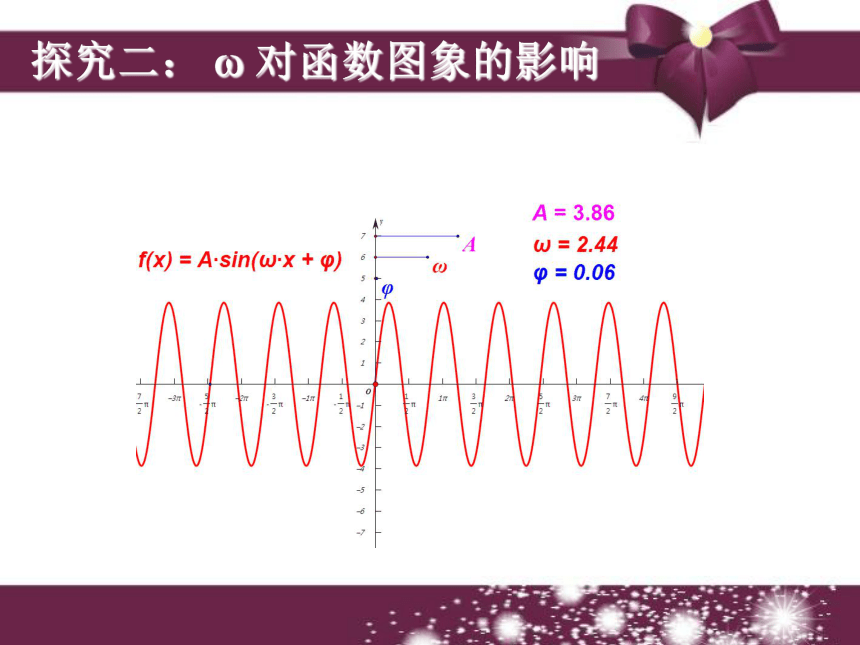
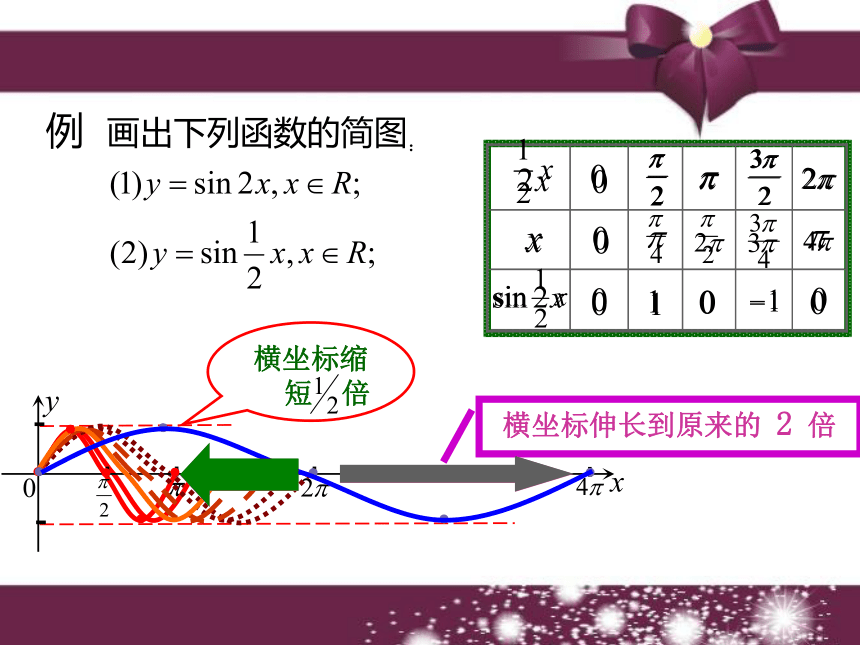
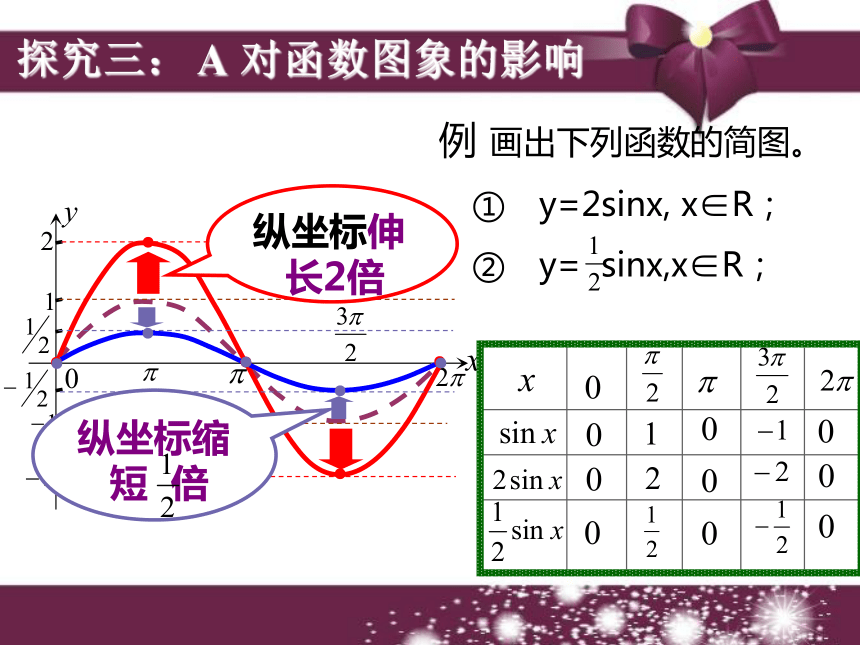
的图象可由y=sinx的图象向右平移 个单位?函数y=sin(x+φ) 的图象可以看作是把 y=sinx 的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平移|φ|个单位而得到的。结论一探究一: 对函数图象的影响探究二: ? 对函数图象的影响●●●●●●●●●●横坐标缩短 倍横坐标伸长到原来的 2 倍 ?函数y=sin?x (? >0且?≠1)的图象可以看作是把 y=sinx 的图象上所有点的横坐标缩短(当?>1时)或伸长(当0 ① y=2sinx, x∈R;
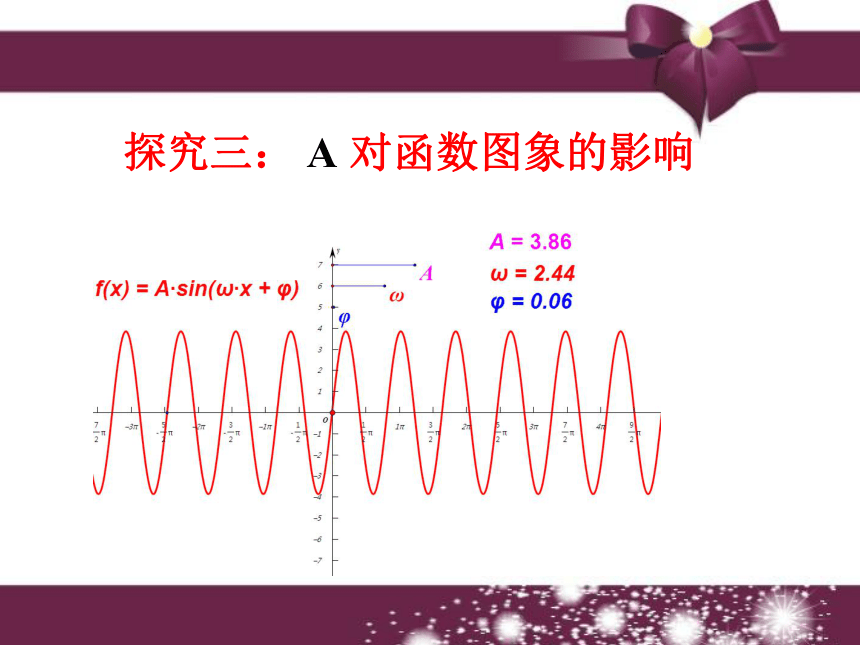
② y= sinx,x∈R;纵坐标伸长2倍纵坐标缩短 倍●●●●●●●●●●探究三: A 对函数图象的影响 ? 函数y=Asinx (A >0且A≠1)的图象可以看作是把 y=sinx 的图象上所有点的纵坐标伸长 (当A>1时)或缩短(当0 向左平
移横坐标压
缩 倍纵坐标伸长 倍思考:刚才的过程中,哪里出错了?思考:y=Asin(ωx+φ)和y=sinx的图象关系课本52页步骤1步骤2步骤3步骤4xyo-11(沿x轴平行移动)(横坐标伸长或缩短)(纵坐标伸长或缩短)改变φ改变ω改变A相位变换周期变换振幅变换周期变换相位变换振幅变换注意:1.(2015年济南模拟)将函数y=cos 2x+1的图象向右平移 个单位长度,再向下平移1个单位长度后得到的函数图象对应的表达式为( )A.y=sin 2x B.y=sin 2x+2A【解析】将函数y=cos 2x+1的图象向右平移个单位长度得到=sin 2x+1,再向下平移1个单位长度得到y=sin 2x全优88页限时规范训练【例3】 (1)求函数的单调递增区间;【解析】(1)则y=sin u在区间上是减函数.全优29页典例剖析【例3】 (1)求函数的单调递增区间;的单调递增区间为(2)求函数的对称轴和对称中心.(2)由于正弦曲线的对称轴是经过函数的最值点且与x轴垂直的直线,正弦曲线的对称中心是曲线与x轴的交点,从而所求对称轴可由所求对称中心的横坐标可由A全优88页限时规范训练物理中简谐振动的相关物理量例2:图是某简谐运动的图象。
问1:这个简谐运动的振幅是多少?物理中简谐振动的相关物理量例2:图是某简谐运动的图象。
问2:从O点算起,到曲线上的哪一点,表示完成了一次往复运动?如从A点算起呢?
物理中简谐振动的相关物理量例2:图是某简谐运动的图象。
问3:这个简谐运动的周期是多少?物理中简谐振动的相关物理量例2:图是某简谐运动的图象。
问4:这个简谐运动的频率是多少?物理中简谐振动的相关物理量例2:图是某简谐运动的图象。
问5:求这个简谐运动的函数表达式.4.(2013年镇江一模)已知ω>0,的周期比振幅小1,则ω=______.1练习:课本56页 35.关于函数 的图象有以下四个结论:
①振幅是-2;
②最小正周期是π;其中正确命题的序号是________.②③④全优30页基础夯实【例2】 函数的图象如下图所示,求函数的表达式.并指出它
的振幅和初相.【解析】由图象可知A=1,函数的周期T=2[3-(-1)]=8=又(1,0)为“五点法”作图的第一个点,全优28页典例剖析【例2】 函数的图象如下图所示,求函数的表达式.并指出它
的振幅和初相.故所求函数的表达式为它的振幅是1,选择的点要认清其属“五点法”中的哪一位置点,并能正确代入列式,求得 .“第一点(第一零点)”为:“第二点(最高点)”为:“第三点(第二零点)”为:“第四点(最低点)”为:“第五点(第三零点)”为:6.已知函数y=Asin(ωx+φ)在同一周期内则此函数的解析式为__________.∴ω=3.全优30页能力提高2.函数y=Asin(ωx+φ)+k(A>0,ω>0)的图象的一部分如图所示,试写出函数的解析式.得周期T=π,即ω=2,全优29页变式训练2.函数y=Asin(ωx+φ)+k(A>0,ω>0)的图象的一部分如图所示,试写出函数的解析式.2.函数y=Asin(ωx+φ)+k(A>0,ω>0)的图象的一部分如图所示,试写出函数的解析式.故所求解析式为
A=_______, ω=______
φ=_______1101.5 函数 的图象探究一: 对函数图象的影响用五点法作出y=sinx的图像整体思想 的图象可由y=sinx的图象向左平移 个单位例? 画出下列函数的简图
1)
2)
的图象可由y=sinx的图象向右平移 个单位?函数y=sin(x+φ) 的图象可以看作是把 y=sinx 的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平移|φ|个单位而得到的。结论一探究一: 对函数图象的影响探究二: ? 对函数图象的影响●●●●●●●●●●横坐标缩短 倍横坐标伸长到原来的 2 倍 ?函数y=sin?x (? >0且?≠1)的图象可以看作是把 y=sinx 的图象上所有点的横坐标缩短(当?>1时)或伸长(当0 ① y=2sinx, x∈R;
② y= sinx,x∈R;纵坐标伸长2倍纵坐标缩短 倍●●●●●●●●●●探究三: A 对函数图象的影响 ? 函数y=Asinx (A >0且A≠1)的图象可以看作是把 y=sinx 的图象上所有点的纵坐标伸长 (当A>1时)或缩短(当0
移横坐标压
缩 倍纵坐标伸长 倍思考:刚才的过程中,哪里出错了?思考:y=Asin(ωx+φ)和y=sinx的图象关系课本52页步骤1步骤2步骤3步骤4xyo-11(沿x轴平行移动)(横坐标伸长或缩短)(纵坐标伸长或缩短)改变φ改变ω改变A相位变换周期变换振幅变换周期变换相位变换振幅变换注意:1.(2015年济南模拟)将函数y=cos 2x+1的图象向右平移 个单位长度,再向下平移1个单位长度后得到的函数图象对应的表达式为( )A.y=sin 2x B.y=sin 2x+2A【解析】将函数y=cos 2x+1的图象向右平移个单位长度得到=sin 2x+1,再向下平移1个单位长度得到y=sin 2x全优88页限时规范训练【例3】 (1)求函数的单调递增区间;【解析】(1)则y=sin u在区间上是减函数.全优29页典例剖析【例3】 (1)求函数的单调递增区间;的单调递增区间为(2)求函数的对称轴和对称中心.(2)由于正弦曲线的对称轴是经过函数的最值点且与x轴垂直的直线,正弦曲线的对称中心是曲线与x轴的交点,从而所求对称轴可由所求对称中心的横坐标可由A全优88页限时规范训练物理中简谐振动的相关物理量例2:图是某简谐运动的图象。
问1:这个简谐运动的振幅是多少?物理中简谐振动的相关物理量例2:图是某简谐运动的图象。
问2:从O点算起,到曲线上的哪一点,表示完成了一次往复运动?如从A点算起呢?
物理中简谐振动的相关物理量例2:图是某简谐运动的图象。
问3:这个简谐运动的周期是多少?物理中简谐振动的相关物理量例2:图是某简谐运动的图象。
问4:这个简谐运动的频率是多少?物理中简谐振动的相关物理量例2:图是某简谐运动的图象。
问5:求这个简谐运动的函数表达式.4.(2013年镇江一模)已知ω>0,的周期比振幅小1,则ω=______.1练习:课本56页 35.关于函数 的图象有以下四个结论:
①振幅是-2;
②最小正周期是π;其中正确命题的序号是________.②③④全优30页基础夯实【例2】 函数的图象如下图所示,求函数的表达式.并指出它
的振幅和初相.【解析】由图象可知A=1,函数的周期T=2[3-(-1)]=8=又(1,0)为“五点法”作图的第一个点,全优28页典例剖析【例2】 函数的图象如下图所示,求函数的表达式.并指出它
的振幅和初相.故所求函数的表达式为它的振幅是1,选择的点要认清其属“五点法”中的哪一位置点,并能正确代入列式,求得 .“第一点(第一零点)”为:“第二点(最高点)”为:“第三点(第二零点)”为:“第四点(最低点)”为:“第五点(第三零点)”为:6.已知函数y=Asin(ωx+φ)在同一周期内则此函数的解析式为__________.∴ω=3.全优30页能力提高2.函数y=Asin(ωx+φ)+k(A>0,ω>0)的图象的一部分如图所示,试写出函数的解析式.得周期T=π,即ω=2,全优29页变式训练2.函数y=Asin(ωx+φ)+k(A>0,ω>0)的图象的一部分如图所示,试写出函数的解析式.2.函数y=Asin(ωx+φ)+k(A>0,ω>0)的图象的一部分如图所示,试写出函数的解析式.故所求解析式为
