华师大版数学八年级下册 专项练习十二 19.3正方形同步练习(含答案)
文档属性
| 名称 | 华师大版数学八年级下册 专项练习十二 19.3正方形同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 374.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-23 00:00:00 | ||
图片预览

文档简介
专项练习十二 正方形
(限时:30分钟 满分:60分)
一、选择题(18分)
1.下列命题错误的是( )
A.对角线互相平分的四边形是平行四边形
B.对角线相等的平行四边形是矩形
C.一条对角线平分一组对角的四边形是菱形
D.对角线互相垂直的矩形是正方形
2.如图,在正方形 ABCD的外侧作等边三角形ADE,则∠AEB 的度数为( )
A.10° B.12.5° C.15° D.20°
3.正方形的周长为 12 cm,则对角线的长为( )
A. 3cm
C.6 cm
4.如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若( 且∠ECF=45°,则CF的长为( )
5.如图,在边长为 2 的正方形ABCD中,M为边 AD 的中点,延长 MD 至点 E,使ME=MC,
以 DE为边作正方形 DEFG,点 G 在边 CD上,则DG的长为( )
6.如图,在正方形 ABCD中,点 E、F 分别为 BC,CD 的中点,则下列结论:①AF⊥DE;②AF=DE;③AD=BP;④PE+ 其中结论正确的有( )
A.1个 B.2个
C.3个 D.4个
二、填空题(15分)
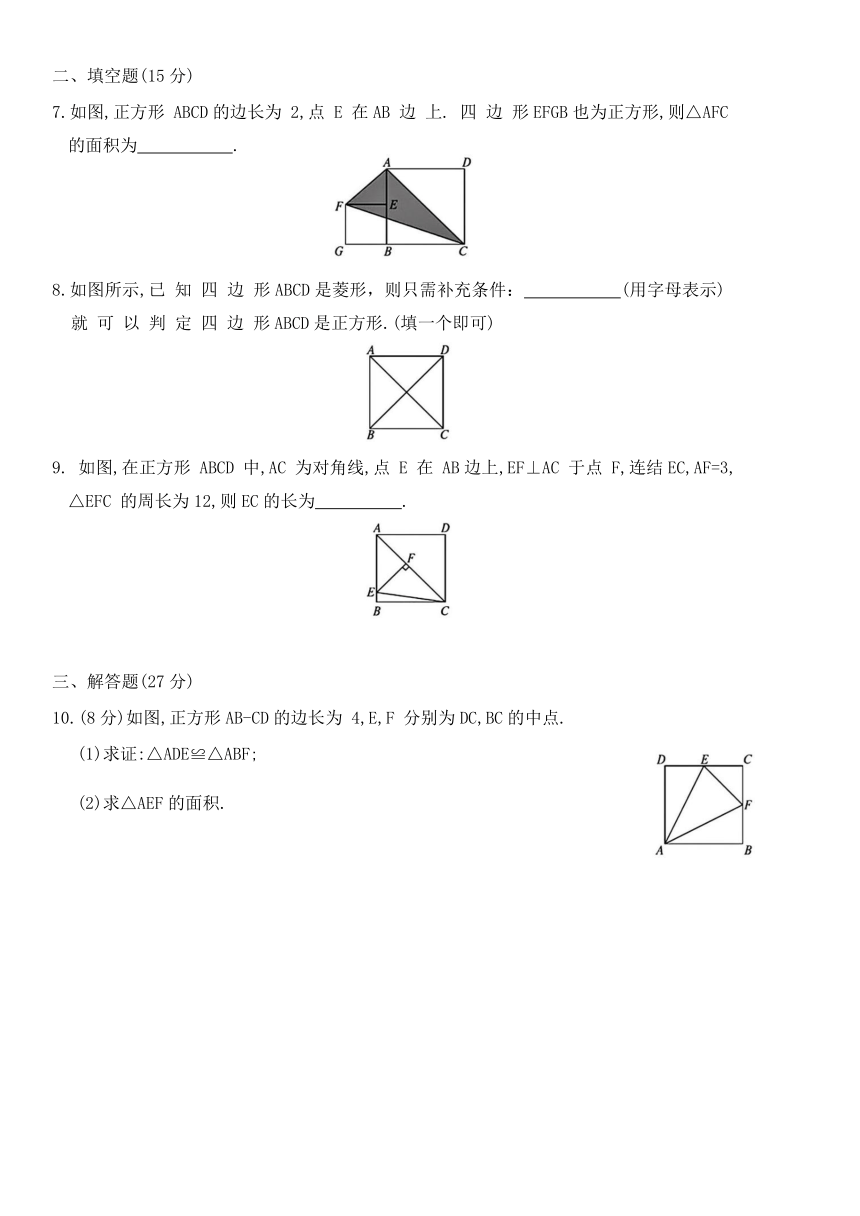
7.如图,正方形 ABCD的边长为 2,点 E 在AB 边 上. 四 边 形EFGB也为正方形,则△AFC的面积为 .
8.如图所示,已 知 四 边 形ABCD是菱形,则只需补充条件: (用字母表示)就 可 以 判 定 四 边 形ABCD是正方形.(填一个即可)
如图,在正方形 ABCD 中,AC 为对角线,点 E 在 AB边上,EF⊥AC 于点 F,连结EC,AF=3,△EFC 的周长为12,则EC的长为 .
三、解答题(27分)
10.(8分)如图,正方形AB-CD的边长为 4,E,F 分别为DC,BC的中点.
(1)求证:△ADE≌△ABF;
(2)求△AEF的面积.
11.(8分)如图,四边形 ABCD中,AD∥BC,AD=CD,E是对角线 BD 上一点,且EA=EC.
(1)求证:四边形 ABCD是菱形;
(2)如果 BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD 是正方形.
12.(11 分)如图,正方形ABCD的边长为6,点 E 在边 AB上,连接 ED,过点D 作FD⊥DE 与 BC 的延长线相交于点F,连接 EF 与边CD 相交于点 G、与对角线 BD 相交于点 H.
(1)若 BD=BF,求 BE的长;
(2)若∠2=2∠1,求证:HF=HE+HD.
专项练习十二 正方形
1. C 2. C 3. B 4. A 5. D 6. D
7.2 8.答案不唯一,如∠ABC=90°或AC=BD等 9.5
10.(1)证明∵四边形ABCD为正方形,
∴AB=AD,∠D=∠B=90°,DC=CB.
∵E,F为DC,BC的中点,
∴DE=BF,在△ADE和△ABF
中,AD=ABD,DE=BF,
∴△ADE≌△ABF(SAS).
(2)解 由题知△ABF,△ADE,△CEF 均为直角三角形,J =2,
11.证明(1)在△ADE与△CDE中,
∴△ADE≌△CDE(SSS),
∴∠ADE=∠CDE,
∵AD∥BC,
∴∠ADE=∠CBD,
∴∠CDE=∠CBD,
∴BC=CD,
∵AD=CD,
∴BC=AD,
∴四边形ABCD 为平行四边形,
∵AD=CD,
∴四边形ABCD 是菱形.
(2)∵BE=BC,
∴∠BCE=∠BEC,
∵∠CBE:∠BCE=2:3,
∵四边形ABCD是菱形,
∴∠ABE=45°,
∴∠ABC=90°,
∴四边形ABCD是正方形.
12.(1)解 ∵四边形ABCD是正方形,且FD⊥DE,∴∠ADE=90°-∠EDC=∠CDF,AD=DC,∠A=∠DCF=90°,
在 Rt△DAE和 Rt△DCF中,
∴Rt△DAE≌Rt△DCF(ASA),
∴AE=CF,
∴BE=AB-AE=AB-CF=6-(6 -6)=12-6 ;
(2)证明在 HF 上取一点P,使FP=EH,连接DP,
由(1)Rt△DAE≌Rt△DCF得△EDF 是等腰直角三角形,
∴DE=DF,∠DEF=∠DFE=45°,
∴△DEH≌△DFP(SAS),
∴DH=DP,∠EDH=∠FDP,在△DHE和△FHB中,
∵∠DEF=∠HBF=45°,∠EHD=∠BHF(对顶角),
∴∠EDH=15°,∠FDP=15°,
∴∠HDP=90°-15°-15°=60°,
∴△DHP 是等边三角形,
∴HD=HP,HF=HE+HD.
(限时:30分钟 满分:60分)
一、选择题(18分)
1.下列命题错误的是( )
A.对角线互相平分的四边形是平行四边形
B.对角线相等的平行四边形是矩形
C.一条对角线平分一组对角的四边形是菱形
D.对角线互相垂直的矩形是正方形
2.如图,在正方形 ABCD的外侧作等边三角形ADE,则∠AEB 的度数为( )
A.10° B.12.5° C.15° D.20°
3.正方形的周长为 12 cm,则对角线的长为( )
A. 3cm
C.6 cm
4.如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若( 且∠ECF=45°,则CF的长为( )
5.如图,在边长为 2 的正方形ABCD中,M为边 AD 的中点,延长 MD 至点 E,使ME=MC,
以 DE为边作正方形 DEFG,点 G 在边 CD上,则DG的长为( )
6.如图,在正方形 ABCD中,点 E、F 分别为 BC,CD 的中点,则下列结论:①AF⊥DE;②AF=DE;③AD=BP;④PE+ 其中结论正确的有( )
A.1个 B.2个
C.3个 D.4个
二、填空题(15分)
7.如图,正方形 ABCD的边长为 2,点 E 在AB 边 上. 四 边 形EFGB也为正方形,则△AFC的面积为 .
8.如图所示,已 知 四 边 形ABCD是菱形,则只需补充条件: (用字母表示)就 可 以 判 定 四 边 形ABCD是正方形.(填一个即可)
如图,在正方形 ABCD 中,AC 为对角线,点 E 在 AB边上,EF⊥AC 于点 F,连结EC,AF=3,△EFC 的周长为12,则EC的长为 .
三、解答题(27分)
10.(8分)如图,正方形AB-CD的边长为 4,E,F 分别为DC,BC的中点.
(1)求证:△ADE≌△ABF;
(2)求△AEF的面积.
11.(8分)如图,四边形 ABCD中,AD∥BC,AD=CD,E是对角线 BD 上一点,且EA=EC.
(1)求证:四边形 ABCD是菱形;
(2)如果 BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD 是正方形.
12.(11 分)如图,正方形ABCD的边长为6,点 E 在边 AB上,连接 ED,过点D 作FD⊥DE 与 BC 的延长线相交于点F,连接 EF 与边CD 相交于点 G、与对角线 BD 相交于点 H.
(1)若 BD=BF,求 BE的长;
(2)若∠2=2∠1,求证:HF=HE+HD.
专项练习十二 正方形
1. C 2. C 3. B 4. A 5. D 6. D
7.2 8.答案不唯一,如∠ABC=90°或AC=BD等 9.5
10.(1)证明∵四边形ABCD为正方形,
∴AB=AD,∠D=∠B=90°,DC=CB.
∵E,F为DC,BC的中点,
∴DE=BF,在△ADE和△ABF
中,AD=ABD,DE=BF,
∴△ADE≌△ABF(SAS).
(2)解 由题知△ABF,△ADE,△CEF 均为直角三角形,J =2,
11.证明(1)在△ADE与△CDE中,
∴△ADE≌△CDE(SSS),
∴∠ADE=∠CDE,
∵AD∥BC,
∴∠ADE=∠CBD,
∴∠CDE=∠CBD,
∴BC=CD,
∵AD=CD,
∴BC=AD,
∴四边形ABCD 为平行四边形,
∵AD=CD,
∴四边形ABCD 是菱形.
(2)∵BE=BC,
∴∠BCE=∠BEC,
∵∠CBE:∠BCE=2:3,
∵四边形ABCD是菱形,
∴∠ABE=45°,
∴∠ABC=90°,
∴四边形ABCD是正方形.
12.(1)解 ∵四边形ABCD是正方形,且FD⊥DE,∴∠ADE=90°-∠EDC=∠CDF,AD=DC,∠A=∠DCF=90°,
在 Rt△DAE和 Rt△DCF中,
∴Rt△DAE≌Rt△DCF(ASA),
∴AE=CF,
∴BE=AB-AE=AB-CF=6-(6 -6)=12-6 ;
(2)证明在 HF 上取一点P,使FP=EH,连接DP,
由(1)Rt△DAE≌Rt△DCF得△EDF 是等腰直角三角形,
∴DE=DF,∠DEF=∠DFE=45°,
∴△DEH≌△DFP(SAS),
∴DH=DP,∠EDH=∠FDP,在△DHE和△FHB中,
∵∠DEF=∠HBF=45°,∠EHD=∠BHF(对顶角),
∴∠EDH=15°,∠FDP=15°,
∴∠HDP=90°-15°-15°=60°,
∴△DHP 是等边三角形,
∴HD=HP,HF=HE+HD.
