数学:1.2《回归分析(1)》课件(苏教版选修1-2)
文档属性
| 名称 | 数学:1.2《回归分析(1)》课件(苏教版选修1-2) |

|
|
| 格式 | rar | ||
| 文件大小 | 62.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-22 14:20:00 | ||
图片预览



文档简介
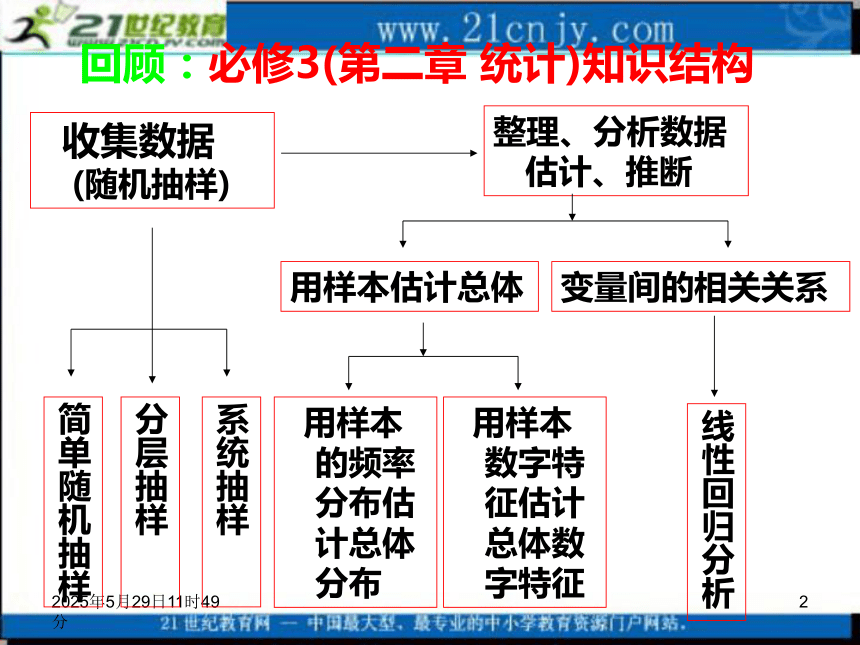
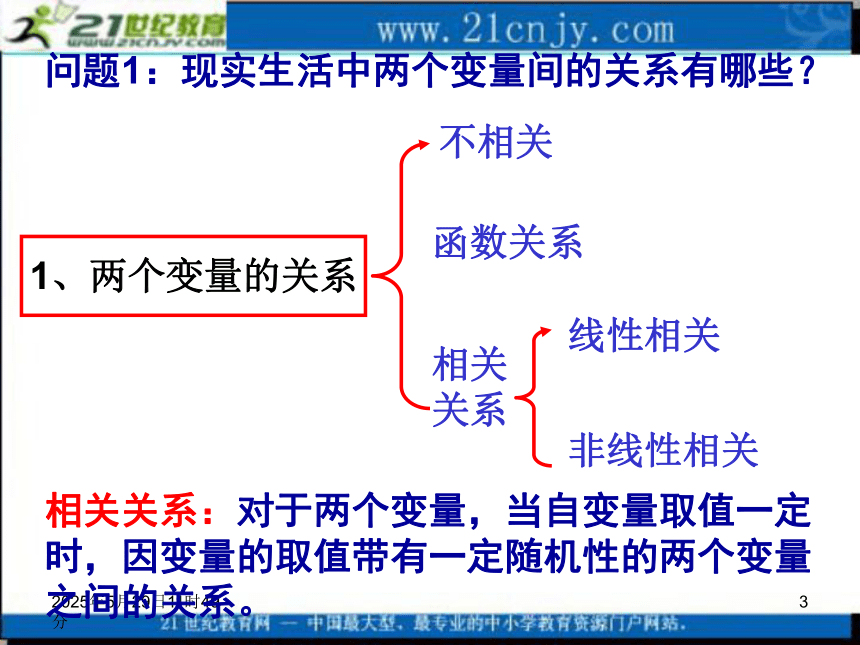
课件21张PPT。2019年3月12日4时8分1回归分析选修1-2(一)2019年3月12日4时8分2回顾:必修3(第二章 统计)知识结构 收集数据 (随机抽样)整理、分析数据估计、推断简单随机抽样分层抽样系统抽样用样本估计总体变量间的相关关系 用样本的频率分布估计总体分布 用样本数字特征估计总体数字特征线性回归分析2019年3月12日4时8分31、两个变量的关系不相关相关关系函数关系线性相关非线性相关问题1:现实生活中两个变量间的关系有哪些?相关关系:对于两个变量,当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系。2019年3月12日4时8分4思考:相关关系与函数关系有怎样的不同?函数关系中的两个变量间是一种确定性关系.
相关关系是一种非确定性关系.函数关系是一种理想的关系模型.
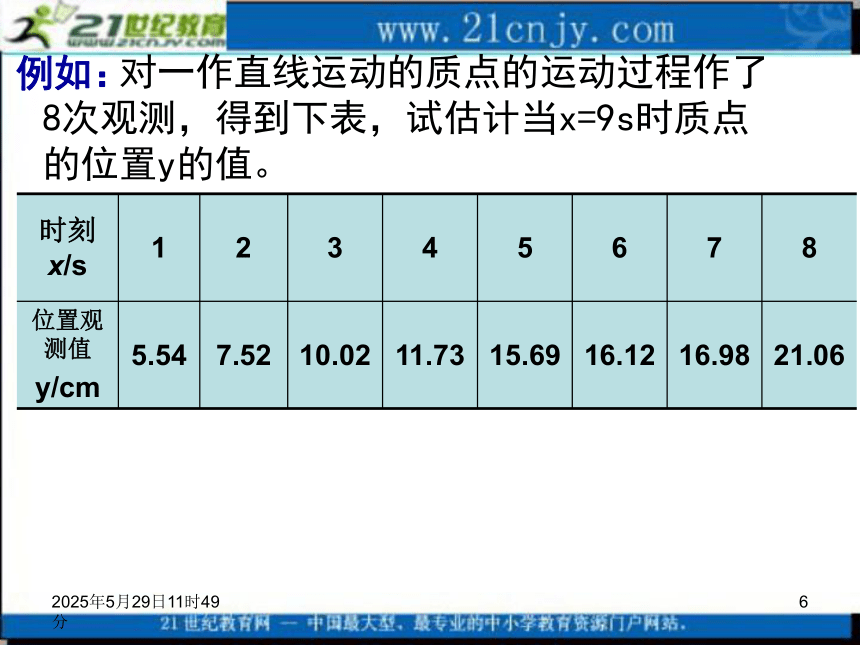
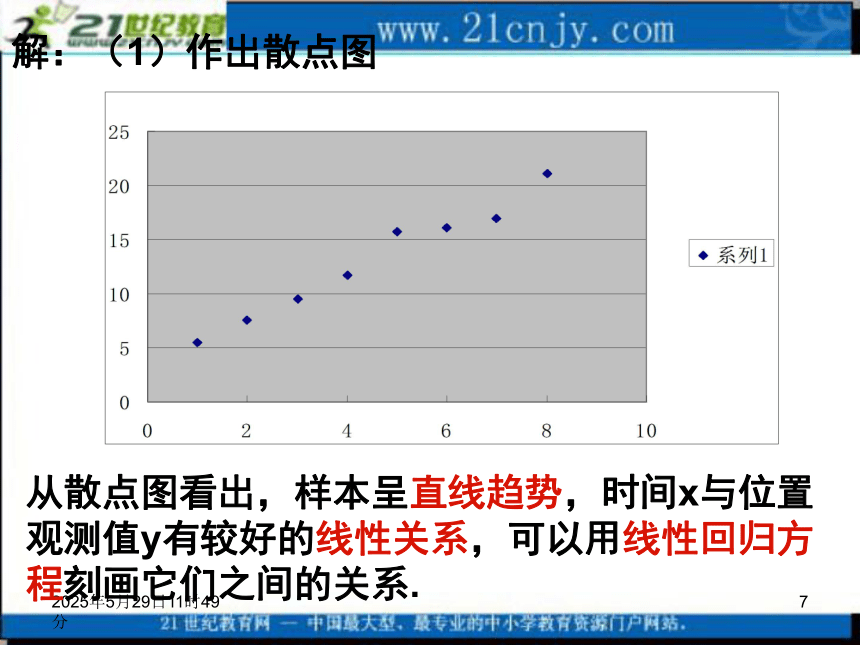
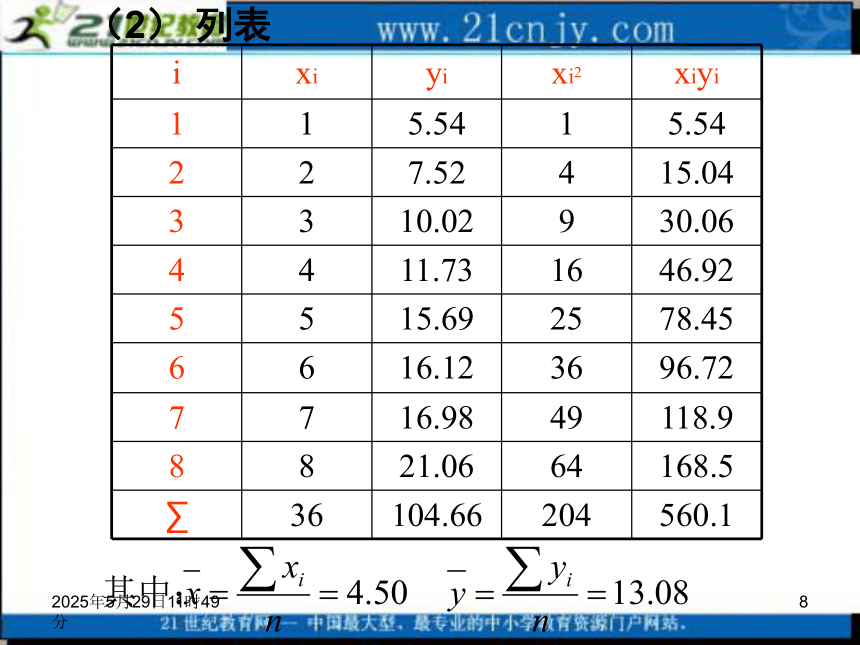
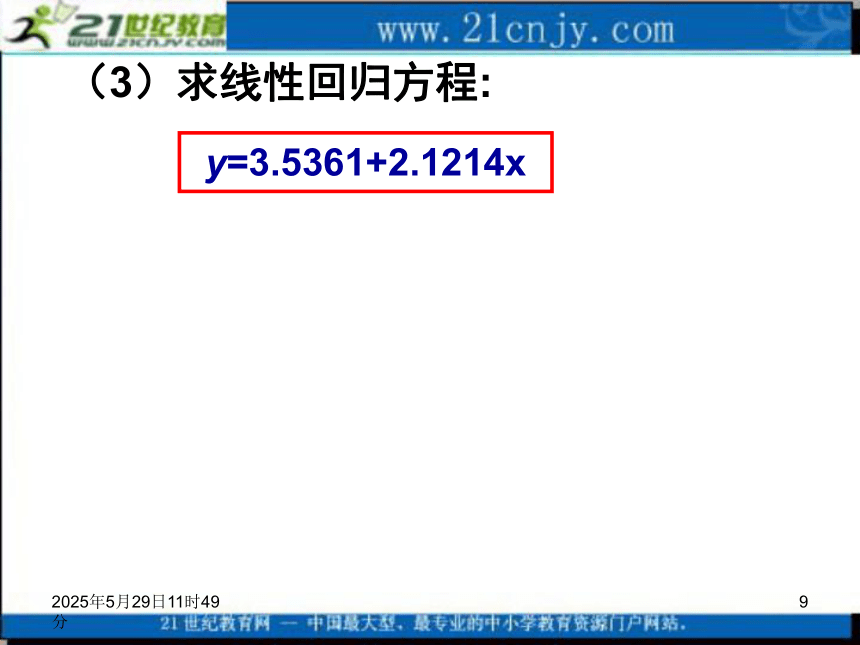
相关关系在现实生活中大量存在,是更一般的情况.2019年3月12日4时8分5问题2:对于线性相关的两个变量用什么方法来刻划之间的关系呢?2、最小二乘估计最小二乘估计下的线性回归方程:2019年3月12日4时8分6 对一作直线运动的质点的运动过程作了8次观测,得到下表,试估计当x=9s时质点的位置y的值。例如:2019年3月12日4时8分7解:(1)作出散点图从散点图看出,样本呈直线趋势,时间x与位置观测值y有较好的线性关系,可以用线性回归方程刻画它们之间的关系.2019年3月12日4时8分8(2) 列表2019年3月12日4时8分9(3)求线性回归方程:y=3.5361+2.1214x2019年3月12日4时8分103、 回归分析的基本步骤:画散点图求回归方程列表2019年3月12日4时8分11数学《必修3》——统计
画出散点图.
求出b,a的值.
求回归直线方程.
用线性回归方程解决应用问题.2019年3月12日4时8分124、线性回归模型其中a+bx是确定性函数, ? 是随机误差注:随机误差? 产生的主要原因:
(1)所用的确定性函数不恰当;
(2)忽略了某些因素的影响;
(3)存在观测误差。思考:在时刻x=9s时,质点运动位置一定是22.6287cm吗?2019年3月12日4时8分13对于线性回归模型
应注意以下两个问题:I 模型的合理性;II 在模型合理的情况下,如何估计a,b.2019年3月12日4时8分14例1.下表给出我国从1949至1999年人口数
据资料,试根据表中数据估计我国2004年
的人口数。分析:先画图2019年3月12日4时8分15解:作出散点图从散点图看出,这些点在一条直线附近,可以用线性回归方程刻画它们之间的关系.2019年3月12日4时8分16列表2019年3月12日4时8分17根据公式得:b=14.453
a=527.591
线性回归方程为:
y=527.591+14.453x
当x=55 时,y=1322.506(百万)2019年3月12日4时8分18例题2.一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,测得数据如下:(1)y与x是否具有线性相关?
(2)若y与x具有线性相关关系,求回归直线方程
(3)预测加工200个零件需花费多少时间?2019年3月12日4时8分19分析:这是一个回归分析问题,应先进行线性相关检验或作散点图来判断x与y是否具有线性相关才可以求解后面的问题。作散点图如下:不难看出x,y成线性相关。2019年3月12日4时8分20解(1)列出下表:2019年3月12日4时8分21问题:有时散点图的各点并不集中在一条直线的附近,仍然可以按照求回归直线方程的步骤求回归直线,显然这样的回归直线没有实际意义。在怎样的情况下求得的回归直线方程才有实际意义?即建立的线性回归模型是否合理?如何对一组数据之间的线性相关程度作出定量分析?
相关关系是一种非确定性关系.函数关系是一种理想的关系模型.
相关关系在现实生活中大量存在,是更一般的情况.2019年3月12日4时8分5问题2:对于线性相关的两个变量用什么方法来刻划之间的关系呢?2、最小二乘估计最小二乘估计下的线性回归方程:2019年3月12日4时8分6 对一作直线运动的质点的运动过程作了8次观测,得到下表,试估计当x=9s时质点的位置y的值。例如:2019年3月12日4时8分7解:(1)作出散点图从散点图看出,样本呈直线趋势,时间x与位置观测值y有较好的线性关系,可以用线性回归方程刻画它们之间的关系.2019年3月12日4时8分8(2) 列表2019年3月12日4时8分9(3)求线性回归方程:y=3.5361+2.1214x2019年3月12日4时8分103、 回归分析的基本步骤:画散点图求回归方程列表2019年3月12日4时8分11数学《必修3》——统计
画出散点图.
求出b,a的值.
求回归直线方程.
用线性回归方程解决应用问题.2019年3月12日4时8分124、线性回归模型其中a+bx是确定性函数, ? 是随机误差注:随机误差? 产生的主要原因:
(1)所用的确定性函数不恰当;
(2)忽略了某些因素的影响;
(3)存在观测误差。思考:在时刻x=9s时,质点运动位置一定是22.6287cm吗?2019年3月12日4时8分13对于线性回归模型
应注意以下两个问题:I 模型的合理性;II 在模型合理的情况下,如何估计a,b.2019年3月12日4时8分14例1.下表给出我国从1949至1999年人口数
据资料,试根据表中数据估计我国2004年
的人口数。分析:先画图2019年3月12日4时8分15解:作出散点图从散点图看出,这些点在一条直线附近,可以用线性回归方程刻画它们之间的关系.2019年3月12日4时8分16列表2019年3月12日4时8分17根据公式得:b=14.453
a=527.591
线性回归方程为:
y=527.591+14.453x
当x=55 时,y=1322.506(百万)2019年3月12日4时8分18例题2.一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,测得数据如下:(1)y与x是否具有线性相关?
(2)若y与x具有线性相关关系,求回归直线方程
(3)预测加工200个零件需花费多少时间?2019年3月12日4时8分19分析:这是一个回归分析问题,应先进行线性相关检验或作散点图来判断x与y是否具有线性相关才可以求解后面的问题。作散点图如下:不难看出x,y成线性相关。2019年3月12日4时8分20解(1)列出下表:2019年3月12日4时8分21问题:有时散点图的各点并不集中在一条直线的附近,仍然可以按照求回归直线方程的步骤求回归直线,显然这样的回归直线没有实际意义。在怎样的情况下求得的回归直线方程才有实际意义?即建立的线性回归模型是否合理?如何对一组数据之间的线性相关程度作出定量分析?
