第二十二章 二次函数 单元试卷 2024-2025学年人教版数学九年级上册(无答案)
文档属性
| 名称 | 第二十二章 二次函数 单元试卷 2024-2025学年人教版数学九年级上册(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 720.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-23 00:00:00 | ||
图片预览


文档简介
第二十二章 二次函数 单元试卷
一、选择题
1.已知实数a,b满足且,则代数式的最小值是( )
A.7 B.4 C.6 D.3
2.已知二次函数,当时,,则二次函数的图象可能为( )
A. B.
C. D.
3.已知一个二次函数的自变量x与函数y的几组对应值如下表,
x … 0 3 5 …
y … 0 …
则下列关于这个二次函数的结论正确的是( )
A.图象的开口向上
B.当时,y的值随x的值增大而增大
C.图象经过第二、三、四象限
D.图象的对称轴是直线
4.无论k取何值,直线与抛物线总有公共点,则a的取值范围是( )
A. B. C.或 D.或
5.在平面直角坐标系中,抛物线如图所示,则关于的方程根的情况为( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法准确判断
6.如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.下列叙述正确的是( )
A.小球的飞行高度不能达到15m B.小球的飞行高度可以达到25m
C.小球从飞出到落地要用时4s D.小球飞出1s时的飞行高度为10m
7.如图所示,已知二次函数y=ax2+bx+c的图像与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=1,则下列结论:①abc>0;②2a+b+c>0;③a﹣b+c<0;④x(ax+b)≤a+b.其中正确结论的个数有( )
A.4个 B.3个 C.2个 D.1个
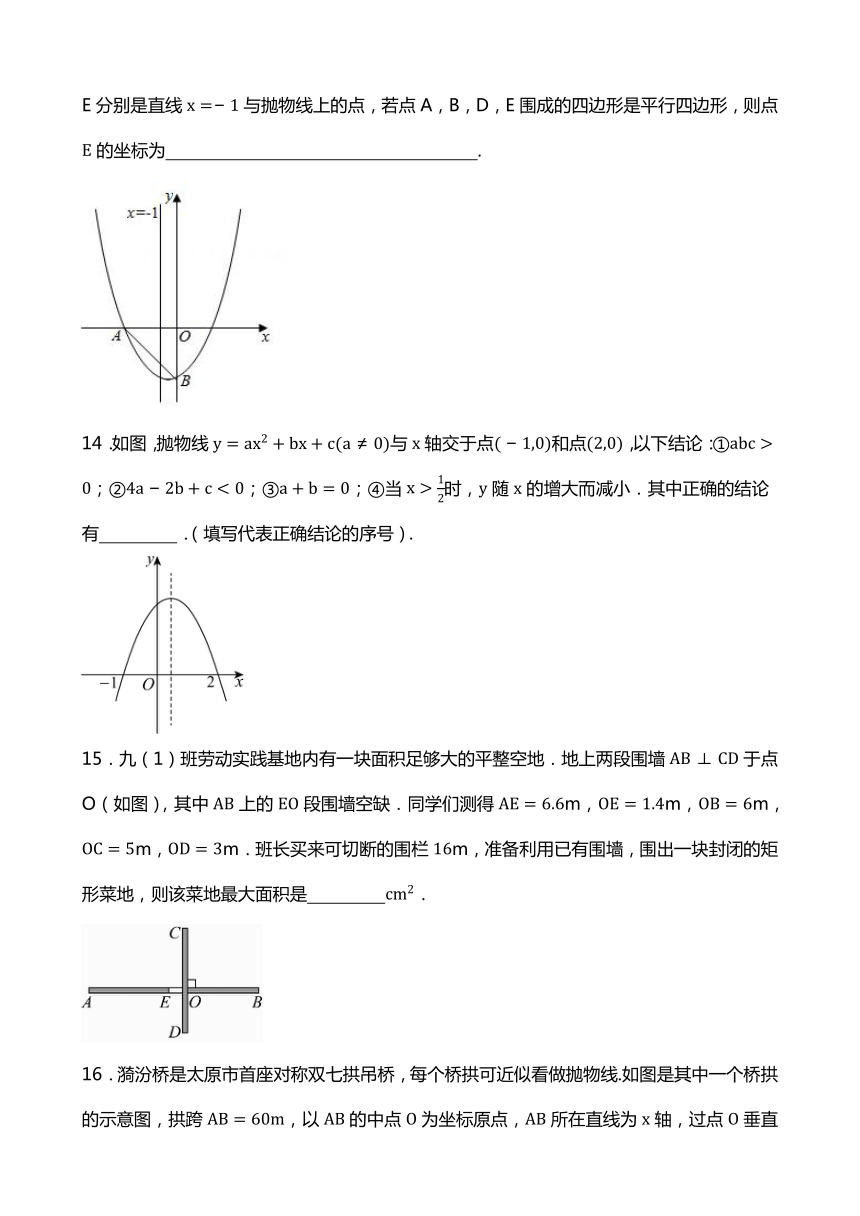
8.最近,吊篮西瓜大量成熟,开园上市,走进某村果蔬基地吊篮西瓜大棚(图1)内,碧绿的藤蔓上一个个生得俊俏、长相甜美的西瓜映入眼帘.如图2是某瓜农的一个横截面为抛物线的大棚,大棚在地面上的宽度是6米,最高点C距地面的距离为2米.以水平地面为x轴,的中点O为原点建立平面直角坐标系.一位身高米的瓜农,若要在大棚内站直行走,则此瓜农从点O沿向左最多能走( )
A.米 B.米 C.3米 D.6米
二、填空题
9.已知是关于x的二次函数,那么m的值为
10.已知抛物线的对称轴在y轴右侧,当时,y随x增大而增大,若抛物线上的点纵坐标,则m的取值范围为
11.已知抛物线的顶点为点,与轴分别交于点,(点在点左侧),抛物线与抛物线关于轴对称,顶点为点,若四边形为正方形,则的值为 .
12.二次函数的图象如图,若一元二次方程有实数根,则的最小值为
13.抛物线与x轴的负半轴交于点,与轴交于点,连接AB,点D,E分别是直线与抛物线上的点,若点A,B,D,E围成的四边形是平行四边形,则点的坐标为 .
14.如图,抛物线与轴交于点和点,以下结论:①;②;③;④当时,随的增大而减小.其中正确的结论有 .(填写代表正确结论的序号).
15.九(1)班劳动实践基地内有一块面积足够大的平整空地.地上两段围墙于点O(如图),其中上的段围墙空缺.同学们测得m,m,m,m,m.班长买来可切断的围栏m,准备利用已有围墙,围出一块封闭的矩形菜地,则该菜地最大面积是 .
16.漪汾桥是太原市首座对称双七拱吊桥,每个桥拱可近似看做抛物线.如图是其中一个桥拱的示意图,拱跨,以的中点为坐标原点,所在直线为轴,过点垂直于的直线为轴建立平面直角坐标系,通过测量得,且,则桥拱最高点到桥面的距离为 m.
三、解答题
17.在平面直角坐标系中,已知抛物线.
(1)当时,求抛物线的顶点坐标;
(2)已知和是抛物线上的两点.若对于,,都有,求a的取值范围.
18.如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,点A的坐标为(﹣1,0),点C的坐标为(0,﹣3),连接BC.
(1)求该二次函数的解析式;
(2)点P是抛物线在第四象限图象上的任意一点,当△BCP的面积最大时,BC边上的高PN的值为 .
19.某超市购入一批进价为10元盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量(盒)与销售单价(元)是一次函数关系,下表是与的几组对应值.
销售单价元 12 14 16 18 20
销售量盒 56 52 48 44 40
(1)求与的函数表达式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少?
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求的值.
20.学校要建一个矩形花圃,其中一边靠墙,另外三边用篱笆围成.已知墙长42米,篱笆长80米.设垂直于墙的边AB长为x米,平行于墙的边BC为y米,围成的矩形面积为S米2.
(1)求y与x,s与x的关系式.
(2)围成的矩形花圃面积能否为750米2,若能,求出x的值.
(3)围成的矩形花圃面积是否存在最大值?若存在,求出这个最大值,并求出此时x的值.
21.如图,抛物线y=x2+bx+c与x轴相交于A、B两点,点A的坐标为(﹣1,0),点B的坐标为(3,0).
(1)求二次函数的解析式;
(2)求△ABC的面积;
(3)若P是第四象限内抛物线上任意一点,PH⊥x轴于点H,与BC交于点M.求线段PM的最大值.
22.甲、乙、丙三名同学玩跳绳,绳被甩到最高处时的形状是如图所示的抛物线,其表达式为.已知拿绳的甲、乙两名同学甩绳时手间距为6米,手到地面的距离和相等,丙同学位于距点D的水平距离为1米的点E处,当跳起后头顶距地面的高度为1.6米时,绳子甩到最高处时刚好擦过丙同学头顶F.以点D为原点建立如图所示的平面直角坐标系.
(1)求此抛物线表达式,并注明x的取值范围.
(2)丁同学跳起后头顶距地面的高度为1.78米,若丁同学也加入游戏,最多能与丙同学水平相距多少米?
23.在平面直角坐标系xOy中,已知抛物线为常数,.
(1)若抛物线与轴交于两点,求抛物线对应的函数表达式;
(2)如图,当时,过点分别作轴的平行线,交抛物线于点M、N,连接MN、MD.求证:MD平分;
(3)当时,过直线上一点作轴的平行线,交抛物线于点.若GH的最大值为4,求的值.
24.如图1,平面直角坐标系中,有抛物线:.设抛物线与轴相交于点,与轴正半轴相交于点,且.
(1)求的值.
(2)如图2,将抛物线平移得到抛物线,使过点和,求抛物线的解析式.
(3)设(2)中在轴左侧的部分与在轴右侧的部分组成的新图象记为.过点作直线平行于轴,与图象交于两点,如图3.
①过的最高点作直线交于点(点在点左侧),求的值;
②是图象上一个动点,当点与直线的距离小于4时,直接写出点横坐标的取值范围.
一、选择题
1.已知实数a,b满足且,则代数式的最小值是( )
A.7 B.4 C.6 D.3
2.已知二次函数,当时,,则二次函数的图象可能为( )
A. B.
C. D.
3.已知一个二次函数的自变量x与函数y的几组对应值如下表,
x … 0 3 5 …
y … 0 …
则下列关于这个二次函数的结论正确的是( )
A.图象的开口向上
B.当时,y的值随x的值增大而增大
C.图象经过第二、三、四象限
D.图象的对称轴是直线
4.无论k取何值,直线与抛物线总有公共点,则a的取值范围是( )
A. B. C.或 D.或
5.在平面直角坐标系中,抛物线如图所示,则关于的方程根的情况为( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法准确判断
6.如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.下列叙述正确的是( )
A.小球的飞行高度不能达到15m B.小球的飞行高度可以达到25m
C.小球从飞出到落地要用时4s D.小球飞出1s时的飞行高度为10m
7.如图所示,已知二次函数y=ax2+bx+c的图像与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=1,则下列结论:①abc>0;②2a+b+c>0;③a﹣b+c<0;④x(ax+b)≤a+b.其中正确结论的个数有( )
A.4个 B.3个 C.2个 D.1个
8.最近,吊篮西瓜大量成熟,开园上市,走进某村果蔬基地吊篮西瓜大棚(图1)内,碧绿的藤蔓上一个个生得俊俏、长相甜美的西瓜映入眼帘.如图2是某瓜农的一个横截面为抛物线的大棚,大棚在地面上的宽度是6米,最高点C距地面的距离为2米.以水平地面为x轴,的中点O为原点建立平面直角坐标系.一位身高米的瓜农,若要在大棚内站直行走,则此瓜农从点O沿向左最多能走( )
A.米 B.米 C.3米 D.6米
二、填空题
9.已知是关于x的二次函数,那么m的值为
10.已知抛物线的对称轴在y轴右侧,当时,y随x增大而增大,若抛物线上的点纵坐标,则m的取值范围为
11.已知抛物线的顶点为点,与轴分别交于点,(点在点左侧),抛物线与抛物线关于轴对称,顶点为点,若四边形为正方形,则的值为 .
12.二次函数的图象如图,若一元二次方程有实数根,则的最小值为
13.抛物线与x轴的负半轴交于点,与轴交于点,连接AB,点D,E分别是直线与抛物线上的点,若点A,B,D,E围成的四边形是平行四边形,则点的坐标为 .
14.如图,抛物线与轴交于点和点,以下结论:①;②;③;④当时,随的增大而减小.其中正确的结论有 .(填写代表正确结论的序号).
15.九(1)班劳动实践基地内有一块面积足够大的平整空地.地上两段围墙于点O(如图),其中上的段围墙空缺.同学们测得m,m,m,m,m.班长买来可切断的围栏m,准备利用已有围墙,围出一块封闭的矩形菜地,则该菜地最大面积是 .
16.漪汾桥是太原市首座对称双七拱吊桥,每个桥拱可近似看做抛物线.如图是其中一个桥拱的示意图,拱跨,以的中点为坐标原点,所在直线为轴,过点垂直于的直线为轴建立平面直角坐标系,通过测量得,且,则桥拱最高点到桥面的距离为 m.
三、解答题
17.在平面直角坐标系中,已知抛物线.
(1)当时,求抛物线的顶点坐标;
(2)已知和是抛物线上的两点.若对于,,都有,求a的取值范围.
18.如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,点A的坐标为(﹣1,0),点C的坐标为(0,﹣3),连接BC.
(1)求该二次函数的解析式;
(2)点P是抛物线在第四象限图象上的任意一点,当△BCP的面积最大时,BC边上的高PN的值为 .
19.某超市购入一批进价为10元盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量(盒)与销售单价(元)是一次函数关系,下表是与的几组对应值.
销售单价元 12 14 16 18 20
销售量盒 56 52 48 44 40
(1)求与的函数表达式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少?
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求的值.
20.学校要建一个矩形花圃,其中一边靠墙,另外三边用篱笆围成.已知墙长42米,篱笆长80米.设垂直于墙的边AB长为x米,平行于墙的边BC为y米,围成的矩形面积为S米2.
(1)求y与x,s与x的关系式.
(2)围成的矩形花圃面积能否为750米2,若能,求出x的值.
(3)围成的矩形花圃面积是否存在最大值?若存在,求出这个最大值,并求出此时x的值.
21.如图,抛物线y=x2+bx+c与x轴相交于A、B两点,点A的坐标为(﹣1,0),点B的坐标为(3,0).
(1)求二次函数的解析式;
(2)求△ABC的面积;
(3)若P是第四象限内抛物线上任意一点,PH⊥x轴于点H,与BC交于点M.求线段PM的最大值.
22.甲、乙、丙三名同学玩跳绳,绳被甩到最高处时的形状是如图所示的抛物线,其表达式为.已知拿绳的甲、乙两名同学甩绳时手间距为6米,手到地面的距离和相等,丙同学位于距点D的水平距离为1米的点E处,当跳起后头顶距地面的高度为1.6米时,绳子甩到最高处时刚好擦过丙同学头顶F.以点D为原点建立如图所示的平面直角坐标系.
(1)求此抛物线表达式,并注明x的取值范围.
(2)丁同学跳起后头顶距地面的高度为1.78米,若丁同学也加入游戏,最多能与丙同学水平相距多少米?
23.在平面直角坐标系xOy中,已知抛物线为常数,.
(1)若抛物线与轴交于两点,求抛物线对应的函数表达式;
(2)如图,当时,过点分别作轴的平行线,交抛物线于点M、N,连接MN、MD.求证:MD平分;
(3)当时,过直线上一点作轴的平行线,交抛物线于点.若GH的最大值为4,求的值.
24.如图1,平面直角坐标系中,有抛物线:.设抛物线与轴相交于点,与轴正半轴相交于点,且.
(1)求的值.
(2)如图2,将抛物线平移得到抛物线,使过点和,求抛物线的解析式.
(3)设(2)中在轴左侧的部分与在轴右侧的部分组成的新图象记为.过点作直线平行于轴,与图象交于两点,如图3.
①过的最高点作直线交于点(点在点左侧),求的值;
②是图象上一个动点,当点与直线的距离小于4时,直接写出点横坐标的取值范围.
同课章节目录
