第4章 图形的平移与旋转 单元测试卷(无答案) 2023--2024学年鲁教版(五四制)八年级数学上册
文档属性
| 名称 | 第4章 图形的平移与旋转 单元测试卷(无答案) 2023--2024学年鲁教版(五四制)八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 158.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-23 16:47:54 | ||
图片预览


文档简介
鲁教版(五四制)八年级上册《第4章图形的平移与旋转》单元测试卷
一、选择题
1. 如图所示的各组图形中,表示平移关系的是( )
A. B. C. D.
2. 下列四个图形中是轴对称图形,但不是中心对称图形的是( )
A. B. C. D.
3. 下列说法中,正确的是( )
A.形状和大小完全相同的两个图形成中心对称
B.成中心对称的两个图形必重合
C.成中心对称的两个图形形状和大小完全相同
D.旋转后能重合的两个图形成中心对称
4. 在直角坐标系中,将点P(3,6)向左平移4个单位长度,再向下平移8个单位长度后,得到的点位于
( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
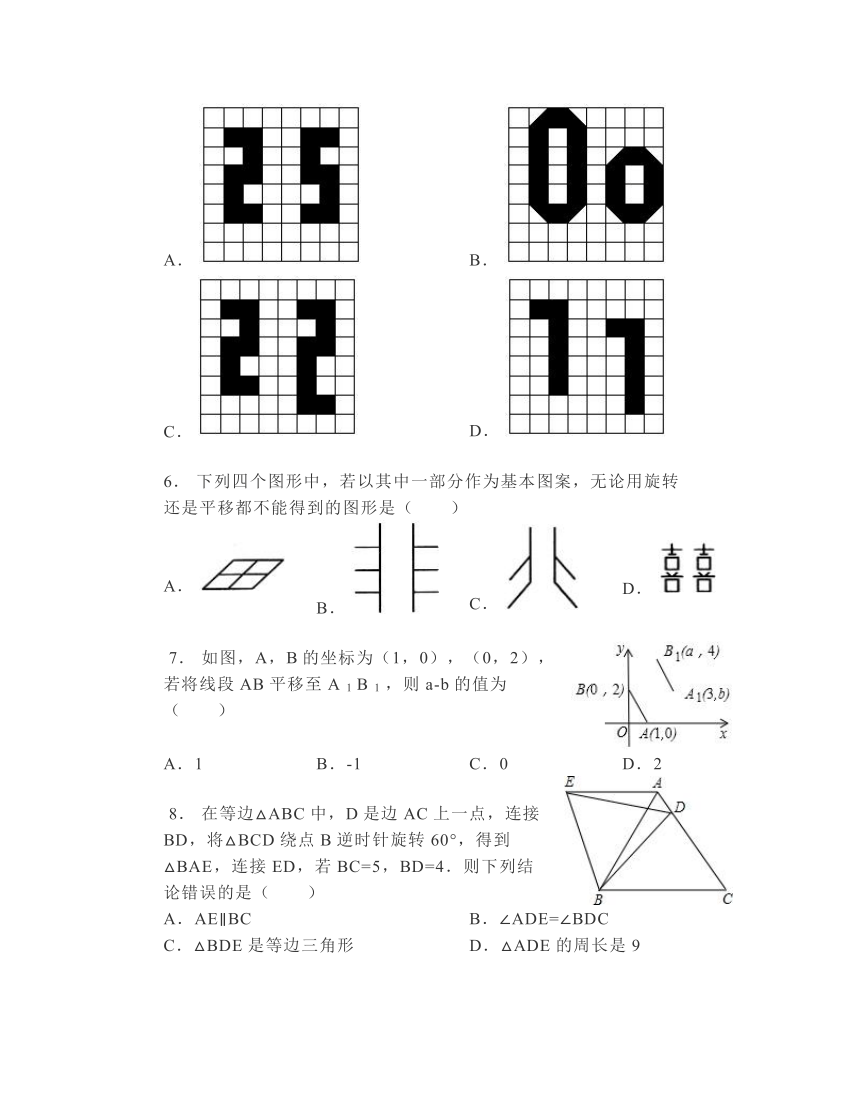
5. 如图所示的网格中各有不同的图案,能通过平移得到的是( )
A. B.
C. D.
6. 下列四个图形中,若以其中一部分作为基本图案,无论用旋转还是平移都不能得到的图形是( )
A. B. C. D.
7. 如图,A,B的坐标为(1,0),(0,2),若将线段AB平移至A 1 B 1 ,则a-b的值为( )
A.1 B.-1 C.0 D.2
8. 在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列结论错误的是( )
A.AE∥BC B.∠ADE=∠BDC
C.△BDE是等边三角形 D.△ADE的周长是9
9. 如图所示,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)、(-2,1),将△ABC沿一确定方向平移得到△A 1 B 1 C 1 ,点B的对应点B 1 的坐标是(1,2),则点A 1 ,C 1 的坐标分别是( )
A.A 1 (4,4),C 1 (3,2) B.A 1 (3,3),C 1 (2,1)
C.A 1 (4,3),C 1 (2,3) D.A 1 (3,4),C 1 (2,2)
10. 如图,Rt△AOB放置在坐标系中,点A的坐标是(1,0),点B的坐标是(0,2),把Rt△AOB绕点A按顺时针旋转90度后得Rt△AO′B′,则B′的坐标是( )
A.(1,2) B.(3,1) C.(1,3) D.(2,3)
二、填空题
11. 在“线段、等腰三角形、四边形、圆”这几个图形中,中心对称图形是 ______ .
12. 已知点A(-2,3),将它先向左平移2个单位,再向上平移3个单位后得到点B,则点B的坐标是 ______ .
13. 认真观察四个图中阴影部分构成的图案,
请写出这四个图案都具有的一个共同特征: ______ .
14. 如图,在平面直角坐标系xOy中,△OCD可以看成是△AOB经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△AOB得到△OCD的过程 ______ .
15. 如图,在平面直角坐标系xOy中,△CDE可以看作是△ABO经过若干次图形的变化(平移、轴对称)得到的,写出一种由△ABO得到△CDE的过程(轴对称,请在图中标出相应的对称轴): ______ .
三、解答题
16. 在直角坐标平面内,已知点A(3,0)、B(-5,3),将点A向左平移6个单位到达C点,将点B向下平移6个单位到达D点.
(1)写出C点、D点的坐标:C ______ ,D ______ ;
(2)把这些点按A、B、C、D、A顺次连接起来,试求这个封闭图形的面积.
17. 如图,由4个全等的正方形组成的L形图案,请按下列要求画图:
(1)在图案①中添加1个正方形,使它成轴对称图形(不能是中心对称图形);
(2)在图案②中添加1个正方形,使它成中心对称图形(不能是轴对称图形);
(3)在图案③中改变1个正方形的位置,从而得到一个新图形,使它既成中心对称图形,又成轴对称图形.
18. 如图,在网格图中(小正方形的边长为1),△ABC的三个顶点都在格点上,直接写出点C的坐标,并把△ABC向右平移4个单位得到△A 1 B 1 C 1 ,再把△A 1 B 1 C 1 沿x轴对称得到△A 2 B 2 C 2 ,请分别作出△A 1 B 1 C 1 与△A 2 B 2 C 2 ,并写出点C 1 和点C 2 的坐标.
19. 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,根据下列要求画出图形.
(1)将△ABC向左平移4个单位长度,再向下平移2个单位长度,画出平移后的△MON;
(2)将△DEF绕D点逆时针旋转90°,画出旋转后的△DGH.
20. 如图,△A′B′C′是△ABC经过平移得到的,△ABC三个顶点的坐标分别为A(-4,-1),B(-5,-4),C(-1,-3),△ABC中任意一点P(x,y)平移后的对应点为P′(x+6,y+4).
(1)请写出三角形ABC平移的过程;
(2)写出点A′,B′,C′的坐标,并画出△A′B′C′.
(3)求△A′B′C′的面积.
21. 按下面的要求画图:
将(1)中的图形沿虚线翻折到(2)的方格中;
将平移后的图形向右平移到(3)的方格中;
将翻折后的图形绕右下角的顶点旋转180°到(4)的方格中.
22. 如图1所示,将一个边长为2的正方形ABCD和一个长为2,宽为1的矩形CEFD拼在一起,构成一个大的矩形ABEF,现将小矩形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α.
(1)当点D′恰好落在EF边上时,求旋转角α的值;
(2)如图2,G为BC中点,且0°<α<90°,求证:GD′=E′D.
一、选择题
1. 如图所示的各组图形中,表示平移关系的是( )
A. B. C. D.
2. 下列四个图形中是轴对称图形,但不是中心对称图形的是( )
A. B. C. D.
3. 下列说法中,正确的是( )
A.形状和大小完全相同的两个图形成中心对称
B.成中心对称的两个图形必重合
C.成中心对称的两个图形形状和大小完全相同
D.旋转后能重合的两个图形成中心对称
4. 在直角坐标系中,将点P(3,6)向左平移4个单位长度,再向下平移8个单位长度后,得到的点位于
( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5. 如图所示的网格中各有不同的图案,能通过平移得到的是( )
A. B.
C. D.
6. 下列四个图形中,若以其中一部分作为基本图案,无论用旋转还是平移都不能得到的图形是( )
A. B. C. D.
7. 如图,A,B的坐标为(1,0),(0,2),若将线段AB平移至A 1 B 1 ,则a-b的值为( )
A.1 B.-1 C.0 D.2
8. 在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列结论错误的是( )
A.AE∥BC B.∠ADE=∠BDC
C.△BDE是等边三角形 D.△ADE的周长是9
9. 如图所示,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)、(-2,1),将△ABC沿一确定方向平移得到△A 1 B 1 C 1 ,点B的对应点B 1 的坐标是(1,2),则点A 1 ,C 1 的坐标分别是( )
A.A 1 (4,4),C 1 (3,2) B.A 1 (3,3),C 1 (2,1)
C.A 1 (4,3),C 1 (2,3) D.A 1 (3,4),C 1 (2,2)
10. 如图,Rt△AOB放置在坐标系中,点A的坐标是(1,0),点B的坐标是(0,2),把Rt△AOB绕点A按顺时针旋转90度后得Rt△AO′B′,则B′的坐标是( )
A.(1,2) B.(3,1) C.(1,3) D.(2,3)
二、填空题
11. 在“线段、等腰三角形、四边形、圆”这几个图形中,中心对称图形是 ______ .
12. 已知点A(-2,3),将它先向左平移2个单位,再向上平移3个单位后得到点B,则点B的坐标是 ______ .
13. 认真观察四个图中阴影部分构成的图案,
请写出这四个图案都具有的一个共同特征: ______ .
14. 如图,在平面直角坐标系xOy中,△OCD可以看成是△AOB经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△AOB得到△OCD的过程 ______ .
15. 如图,在平面直角坐标系xOy中,△CDE可以看作是△ABO经过若干次图形的变化(平移、轴对称)得到的,写出一种由△ABO得到△CDE的过程(轴对称,请在图中标出相应的对称轴): ______ .
三、解答题
16. 在直角坐标平面内,已知点A(3,0)、B(-5,3),将点A向左平移6个单位到达C点,将点B向下平移6个单位到达D点.
(1)写出C点、D点的坐标:C ______ ,D ______ ;
(2)把这些点按A、B、C、D、A顺次连接起来,试求这个封闭图形的面积.
17. 如图,由4个全等的正方形组成的L形图案,请按下列要求画图:
(1)在图案①中添加1个正方形,使它成轴对称图形(不能是中心对称图形);
(2)在图案②中添加1个正方形,使它成中心对称图形(不能是轴对称图形);
(3)在图案③中改变1个正方形的位置,从而得到一个新图形,使它既成中心对称图形,又成轴对称图形.
18. 如图,在网格图中(小正方形的边长为1),△ABC的三个顶点都在格点上,直接写出点C的坐标,并把△ABC向右平移4个单位得到△A 1 B 1 C 1 ,再把△A 1 B 1 C 1 沿x轴对称得到△A 2 B 2 C 2 ,请分别作出△A 1 B 1 C 1 与△A 2 B 2 C 2 ,并写出点C 1 和点C 2 的坐标.
19. 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,根据下列要求画出图形.
(1)将△ABC向左平移4个单位长度,再向下平移2个单位长度,画出平移后的△MON;
(2)将△DEF绕D点逆时针旋转90°,画出旋转后的△DGH.
20. 如图,△A′B′C′是△ABC经过平移得到的,△ABC三个顶点的坐标分别为A(-4,-1),B(-5,-4),C(-1,-3),△ABC中任意一点P(x,y)平移后的对应点为P′(x+6,y+4).
(1)请写出三角形ABC平移的过程;
(2)写出点A′,B′,C′的坐标,并画出△A′B′C′.
(3)求△A′B′C′的面积.
21. 按下面的要求画图:
将(1)中的图形沿虚线翻折到(2)的方格中;
将平移后的图形向右平移到(3)的方格中;
将翻折后的图形绕右下角的顶点旋转180°到(4)的方格中.
22. 如图1所示,将一个边长为2的正方形ABCD和一个长为2,宽为1的矩形CEFD拼在一起,构成一个大的矩形ABEF,现将小矩形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α.
(1)当点D′恰好落在EF边上时,求旋转角α的值;
(2)如图2,G为BC中点,且0°<α<90°,求证:GD′=E′D.
