第5章位置与坐标 单元测试卷 (无答案)2024—2025学年鲁教版(五四制)数学七年级上册
文档属性
| 名称 | 第5章位置与坐标 单元测试卷 (无答案)2024—2025学年鲁教版(五四制)数学七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 105.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-23 21:44:53 | ||
图片预览

文档简介
鲁教版(五四制)七年级上册《第5章位置与坐标》单元测试卷
一、选择题
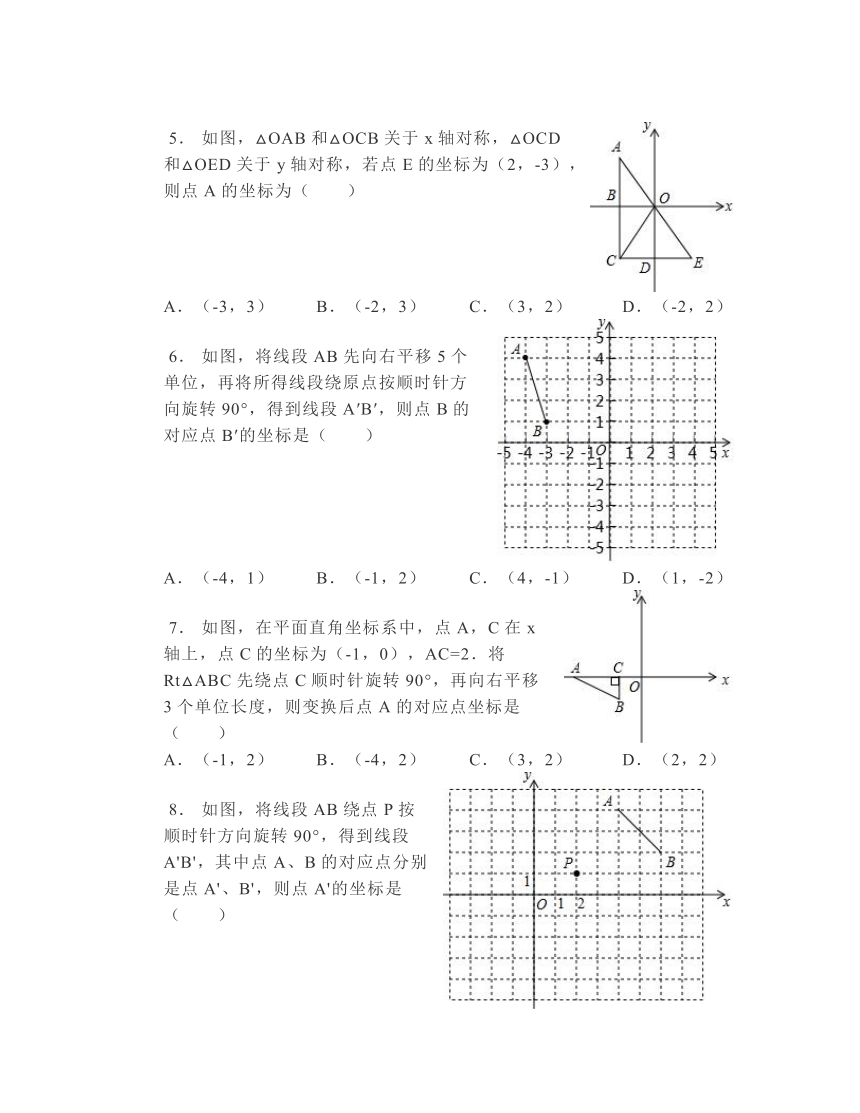
1. 小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是( )
A.(-2,1) B.(-1,1) C.(1,-2) D.(-1,-2)
2. 如图为A、B、C三点在坐标平面上的位置图.若A、B、C的x坐标的数字总和为a,y坐标的数字总和为b,则a-b之值为何?( )
A.5 B.3 C.-3 D.-5
3. 在平面直角坐标系中,将点A(1,2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,则点B的坐标是( )
A.(-1,5) B.(3,1) C.(4,-4) D.(4,0)
4. 如图是小明、小刚和小红做课间操时的位置,老师建立一个平面直角坐标系,如果用坐标(4,5)表示小明的位置,坐标(2,4)表示小刚的位置,那么小红的位置坐标为( )
A.(1,3) B.(-2,3) C.(-1,3) D.(0,2)
5. 如图,△OAB和△OCB关于x轴对称,△OCD和△OED关于y轴对称,若点E的坐标为(2,-3),则点A的坐标为( )
A.(-3,3) B.(-2,3) C.(3,2) D.(-2,2)
6. 如图,将线段AB先向右平移5个单位,再将所得线段绕原点按顺时针方向旋转90°,得到线段A′B′,则点B的对应点B′的坐标是( )
A.(-4,1) B.(-1,2) C.(4,-1) D.(1,-2)
7. 如图,在平面直角坐标系中,点A,C在x轴上,点C的坐标为(-1,0),AC=2.将Rt△ABC先绕点C顺时针旋转90°,再向右平移3个单位长度,则变换后点A的对应点坐标是( )
A.(-1,2) B.(-4,2) C.(3,2) D.(2,2)
8. 如图,将线段AB绕点P按顺时针方向旋转90°,得到线段A'B',其中点A、B的对应点分别是点A'、B',则点A'的坐标是( )
A.(-1,3) B.(4,0) C.(3,-3) D.(5,-1)
9. 在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出下列定义:若b′= ,则称点Q为点的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(-2,5)的限变点的坐标是(-2,-5),如果一个点的限变点的坐标是( ,-1),那么这个点的坐标是( )
A.(-1, ) B.(- ,-1) C.( ,-1) D.( ,1)
10. 在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A 1 ,第2次移动到A 2 ,…,第n次移动到A n .则△OA 2 A 2018 的面积是( )
A.504m 2 B. m 2 C. m 2 D.1009m 2
二、填空题
11. 如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“兵”的坐标分别是(3,0)和(-3,2),那么“卒”的坐标为 ______ .
12. 点P(a,1-3a)是第二象限内的一个点,且点P到两坐标轴的距离之和为5,则点P的坐标是 ______ .
13. 如图的围棋盘放在某个平面直角坐标系内,白棋②的坐标为(-8,-5),白棋④的坐标为(-7,-9),那么黑棋①的坐标应该是 ______ .
14. 在平面直角坐标系中,点P(2,4)关于直线x=1的对称点的坐标是 ______ .
15. 如果点P在第二象限内,点P到x轴的距离是3,到y轴的距离是2,那么点P的坐标为 ______ .
16. 已知平面内有一点A的横坐标为-6,且到原点的距离等于10,则A点的坐标为 ______ .
17. 在平面直角坐标系中,若点M(-2,3)与点N(x,3)之间的距离是5,则x的值是 ______ .
三、解答题
18. 如图,一个小正方形网格的边长表示50米,A同学上学时从家中出发,先向东走250米,再向北走50米就到达学校.
(1)以学校为坐标原点,向东为x轴正方向,向北为y轴正方向,在图中建立直角坐标系;
(2)B同学家的坐标是 ______ ,C同学家的坐标是 ______ ;
(3)在你所建的直角坐标系中,如果D同学家的坐标为(-150,100),请你在图中描出表示D同学的家的点.
19. 长方形ABCD,长为6,宽为4,建坐标系使其中C点的坐标(-3,2),并且求出其它顶点的坐标.
20. 在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(-4,6),(-1,4).
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC关于x轴对称的△A 1 B 1 C 1 ;
(3)请在y轴上求作一点P,使△PB 1 C的周长最小,并直接写出点P的坐标;
(4)请求出△ABC的面积.
一、选择题
1. 小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是( )
A.(-2,1) B.(-1,1) C.(1,-2) D.(-1,-2)
2. 如图为A、B、C三点在坐标平面上的位置图.若A、B、C的x坐标的数字总和为a,y坐标的数字总和为b,则a-b之值为何?( )
A.5 B.3 C.-3 D.-5
3. 在平面直角坐标系中,将点A(1,2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,则点B的坐标是( )
A.(-1,5) B.(3,1) C.(4,-4) D.(4,0)
4. 如图是小明、小刚和小红做课间操时的位置,老师建立一个平面直角坐标系,如果用坐标(4,5)表示小明的位置,坐标(2,4)表示小刚的位置,那么小红的位置坐标为( )
A.(1,3) B.(-2,3) C.(-1,3) D.(0,2)
5. 如图,△OAB和△OCB关于x轴对称,△OCD和△OED关于y轴对称,若点E的坐标为(2,-3),则点A的坐标为( )
A.(-3,3) B.(-2,3) C.(3,2) D.(-2,2)
6. 如图,将线段AB先向右平移5个单位,再将所得线段绕原点按顺时针方向旋转90°,得到线段A′B′,则点B的对应点B′的坐标是( )
A.(-4,1) B.(-1,2) C.(4,-1) D.(1,-2)
7. 如图,在平面直角坐标系中,点A,C在x轴上,点C的坐标为(-1,0),AC=2.将Rt△ABC先绕点C顺时针旋转90°,再向右平移3个单位长度,则变换后点A的对应点坐标是( )
A.(-1,2) B.(-4,2) C.(3,2) D.(2,2)
8. 如图,将线段AB绕点P按顺时针方向旋转90°,得到线段A'B',其中点A、B的对应点分别是点A'、B',则点A'的坐标是( )
A.(-1,3) B.(4,0) C.(3,-3) D.(5,-1)
9. 在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出下列定义:若b′= ,则称点Q为点的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(-2,5)的限变点的坐标是(-2,-5),如果一个点的限变点的坐标是( ,-1),那么这个点的坐标是( )
A.(-1, ) B.(- ,-1) C.( ,-1) D.( ,1)
10. 在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A 1 ,第2次移动到A 2 ,…,第n次移动到A n .则△OA 2 A 2018 的面积是( )
A.504m 2 B. m 2 C. m 2 D.1009m 2
二、填空题
11. 如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“兵”的坐标分别是(3,0)和(-3,2),那么“卒”的坐标为 ______ .
12. 点P(a,1-3a)是第二象限内的一个点,且点P到两坐标轴的距离之和为5,则点P的坐标是 ______ .
13. 如图的围棋盘放在某个平面直角坐标系内,白棋②的坐标为(-8,-5),白棋④的坐标为(-7,-9),那么黑棋①的坐标应该是 ______ .
14. 在平面直角坐标系中,点P(2,4)关于直线x=1的对称点的坐标是 ______ .
15. 如果点P在第二象限内,点P到x轴的距离是3,到y轴的距离是2,那么点P的坐标为 ______ .
16. 已知平面内有一点A的横坐标为-6,且到原点的距离等于10,则A点的坐标为 ______ .
17. 在平面直角坐标系中,若点M(-2,3)与点N(x,3)之间的距离是5,则x的值是 ______ .
三、解答题
18. 如图,一个小正方形网格的边长表示50米,A同学上学时从家中出发,先向东走250米,再向北走50米就到达学校.
(1)以学校为坐标原点,向东为x轴正方向,向北为y轴正方向,在图中建立直角坐标系;
(2)B同学家的坐标是 ______ ,C同学家的坐标是 ______ ;
(3)在你所建的直角坐标系中,如果D同学家的坐标为(-150,100),请你在图中描出表示D同学的家的点.
19. 长方形ABCD,长为6,宽为4,建坐标系使其中C点的坐标(-3,2),并且求出其它顶点的坐标.
20. 在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(-4,6),(-1,4).
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC关于x轴对称的△A 1 B 1 C 1 ;
(3)请在y轴上求作一点P,使△PB 1 C的周长最小,并直接写出点P的坐标;
(4)请求出△ABC的面积.
