第三章圆专题练习(无答案)2023-2024学年 北师大版数学九年级下册
文档属性
| 名称 | 第三章圆专题练习(无答案)2023-2024学年 北师大版数学九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 384.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-23 21:52:08 | ||
图片预览




文档简介
圆
一.圆的认识
1.某公园计划砌一个形状如图(1)所示的喷水池,后来有人建议改为图(2)的形状,且外圆的直径不变,喷水池边沿的宽度、高度不变,你认为砌喷水池的边沿( )
A.图(1)需要的材料多 B.图(2)需要的材料多
C.图(1)、图(2)需要的材料一样多 D.无法确定
二.垂径定理
1.如图,在⊙O中,弦AB=4,圆心O到AB的距离OC=1,则⊙O的半径长为( )
A.2 B.2 C. D.
2.已知⊙O的半径为5,点O到弦AB的距离为3,则⊙O上到弦AB所在直线的距离为2的点有( )
A.4个 B.3个 C.2个 D.1个
3.如图,⊙O的半径为6,将劣弧沿弦AB翻折,恰好经过圆心O,点C为优弧AB上的一个动点,则△ABC面积的最大值是( )
A. B. C. D.
4.下列说法中正确的个数有( )
①平分弦的直径一定垂直于弦;②圆是轴对称图形,每一条直径都是对称轴;③直径是弦;④长度相等的弧是等弧
A.1个 B.2个 C.3个 D.4个
5.如图,线段CD是⊙O的直径,CD⊥AB于点E,若AB长为16,OE长为6,则⊙O半径是( )
A.5 B.6 C.8 D.10
6.如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( )
A.3≤OM≤5 B.4≤OM≤5 C.3<OM<5 D.4<OM<5
三.垂径定理的应用
1.如图,武汉晴川桥可以近似地看作半径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB长度为300m,那么这些钢索中最长的一根为( )
A.50m B.45m C.40m D.60m
2.如图,某隧道的截面是一个半径为3.4米的半圆形,一辆宽3.2米的厢式卡车(截面是长方形)恰好能通过该隧道,则这辆卡车的高为多少米?
四.圆心角、弧、弦的关系
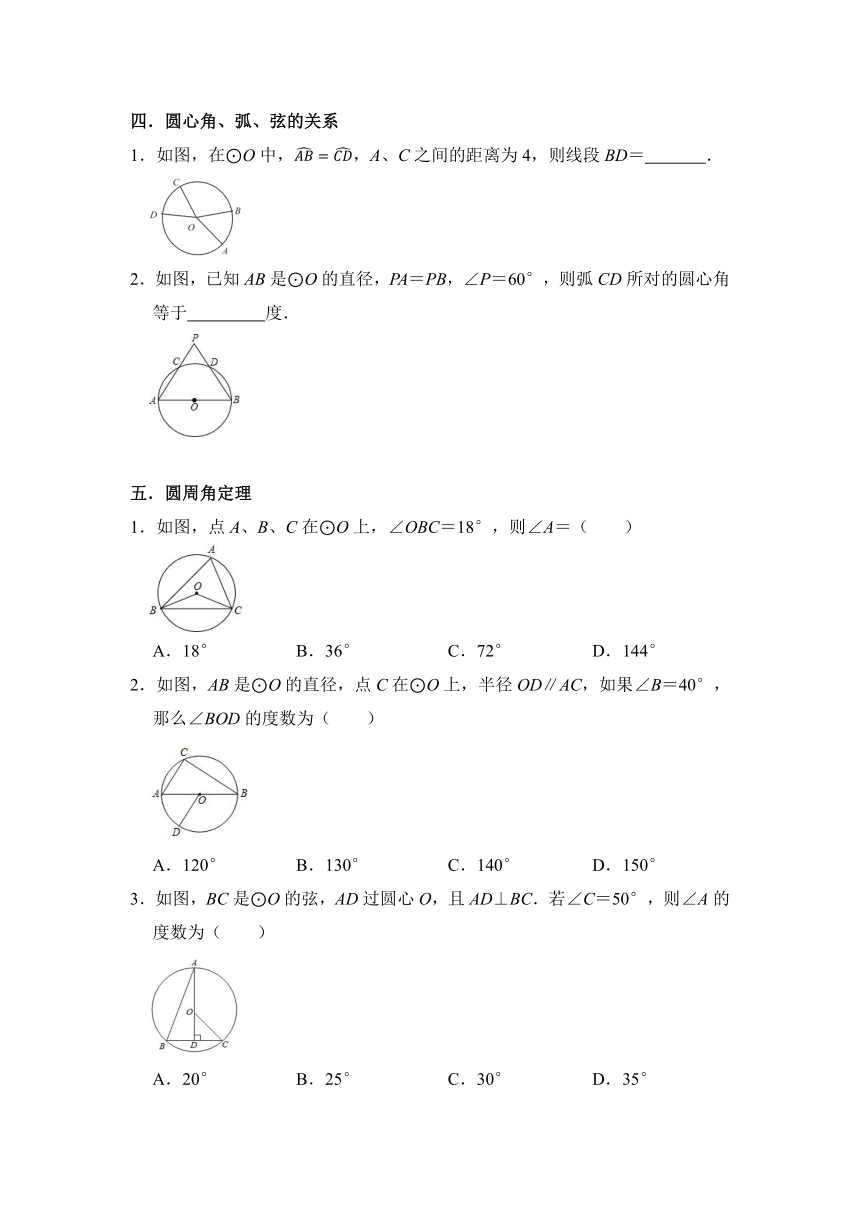
1.如图,在⊙O中,,A、C之间的距离为4,则线段BD= .
2.如图,已知AB是⊙O的直径,PA=PB,∠P=60°,则弧CD所对的圆心角等于 度.
五.圆周角定理
1.如图,点A、B、C在⊙O上,∠OBC=18°,则∠A=( )
A.18° B.36° C.72° D.144°
2.如图,AB是⊙O的直径,点C在⊙O上,半径OD∥AC,如果∠B=40°,那么∠BOD的度数为( )
A.120° B.130° C.140° D.150°
3.如图,BC是⊙O的弦,AD过圆心O,且AD⊥BC.若∠C=50°,则∠A的度数为( )
A.20° B.25° C.30° D.35°
4.如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则( )
A.3α+β=180° B.2α+β=180° C.3α﹣β=90° D.2α﹣β=90°
5.如图,⊙O为△ABC的外接圆,∠BAC=55°,则∠OBC的度数为( )
A.25° B.35° C.55° D.70°
6.如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则∠OBC的正弦值为( )
A. B. C. D.
7.如图,⊙O是△ABC的外接圆,已知∠ACO=30°,则∠B的度数是( )
A.30° B.45° C.60° D.75°
六.圆内接四边形的性质
1.如图,四边形ABCD内接于⊙O,AB=BC,连接OA、OB,∠BAO=70°,则∠D=( )
A.40° B.60° C.45° D.30°
2.如图,四边形ABCD内接于⊙O,AB是直径,OD∥BC,若∠C=124°,则∠B的度数为( )
A.56° B.68° C.72° D.78°
3.如图,四边形ABCD为⊙O的内接四边形,若四边形OBCD为菱形,则∠BAD的度数为( )
A.45° B.60° C.72° D.36°
4.如图,A,B,C,D是圆O上的四个点,点B是弧ABC的中点,如果∠ABC=72°,那么∠ADB= .
七.点与圆的位置关系
1.已知在平面直角坐标系中,P点坐标为(3,4),若以原点O为圆心,半径为5画圆,则点P与⊙O的位置关系是( )
A.点在圆内 B.点在圆上
C.点在圆外 D.不能确定
2.已知⊙O的半径为5,A为线段OP的中点,若OP=8,则点A与⊙O的位置关系是( )
A.点A在⊙O内 B.点A在⊙O上
C.点A在⊙O外 D.不确定
八.确定圆的条件
1.下列说法正确的是( )
A.三点确定一个圆
B.圆心角的度数等于圆周角的两倍
C.与半径垂直的直线是圆的切线
D.在同圆或等圆中,相等的圆周角所对的弦、弧分别相等
九.三角形的外接圆与外心
1.如图,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,⊙D经过A,B,O,C四点,∠ACO=120°,AB=4,则圆心点D的坐标是( )
A. B. C. D.
2.三角形的外心是三角形中( )
A.三条高的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
3.如图,△ABC内接于⊙O,AC是⊙O的直径,∠ACB=40°,点D是劣弧上一点,连接CD、BD,则∠D的度数是( )
A.50° B.45° C.140° D.130°
4.如图,O是△ABC的外心,则∠1+∠2+∠3=( )
A.60° B.75° C.90° D.105°
5.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,若AD=10,∠B=30°,则AC的长度为( )
A.3 B.4 C.5 D.10
十.直线与圆的位置关系
1.已知⊙O的半径为3,圆心O到直线l的距离为2,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
2.已知⊙O的半径为3cm,圆心O到直线l的距离是2cm,则直线l与⊙O的位置关系是 .
十一.切线的性质
1.如图,AB是⊙O的弦,AC是⊙O切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于( )
A.20° B.25° C.40° D.50°
2.如图,PA,PB分别与⊙O相切于A,B两点,∠P=72°,则∠C的度数为( )
A.36° B.54° C.72° D.108°
3.如图,菱形OABC的顶点A,B,C在⊙O上,过点B作⊙O的切线交OA的延长线于点D.若⊙O的半径为1,则BD的长为( )
A.1 B.2 C. D.
4.如图,AB是⊙O的直径,点C、D均在⊙O上,且AC平分∠DAB,过点C作⊙O的切线交AB的延长线于点P,连接BD.
(1)求证:BD∥CP;
(2)若sinP,BP=2,求BD的长.
5.如图,AB是半圆的直径,弦CD∥AB,过D点作圆O的切线DE,与AB延长线相交于点E,连接OC、AD,∠A=22.5°.
(1)求证:四边形COED是平行四边形;
(2)当CD=2时,求围成阴影部分图形的周长.
十二.切线的判定
1.如图,在△ABC中,AB=BC,CO平分∠ACB交AB于点O.当AC=CO时,以点O为圆心OA为半径作圆交AC于点D,过点D作DE⊥BC垂足为E.
(1)求∠B的度数;
(2)证明:DE是⊙O的切线.
十三.切线的判定与性质
1.如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;
(3)PO=AB;(4)∠PDB=120°.其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
十四.弦切角定理
1.如图,直线AB切⊙O于点A,割线BDC交⊙O于点D、C.若∠C=30°,∠B=20°,则∠ADC=( )
A.70° B.50° C.30° D.20°
十五.切割线定理
1.如图,从⊙O外一点A作⊙O的切线AB、AC,切点分别为B、C,且⊙O直径BD=6,连接CD、AO.
(1)求证:CD∥AO;
(2)设CD=x,AO=y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)若AO+CD=11,求AB的长.
十六.三角形的内切圆与内心
1.到三角形三条边的距离相等的点是三角形( )的交点.
A.三个内角平分线 B.三边垂直平分线
C.三条中线 D.三条高线
2.如图,△ABC中,∠ABC=50°,∠ACB=74°,点O是△ABC的内心.则∠BOC等于( )
A.124° B.118° C.112° D.62°
3.如图,⊙O的直径AB为10cm,弦BC为8cm,∠ACB的平分线交⊙O于点D,△ADB的内切圆半径是( )
A. B.5(1) C.5(1) D.
十七.正多边形和圆
1.若⊙O的内接正n边形的边长与⊙O的半径相等,则n的值为( )
A.4 B.5 C.6 D.7
2.已知圆的半径是2,则该圆的内接正六边形的面积是( )
A.3 B.9 C.18 D.36
3.如图,正六边形ABCDEF的边长为6,以顶点A为圆心,AB的长为半径画圆,则图中阴影部分的面积为( )
A.4π B.6π C.8π D.12π
4.如图,已知圆O的内接正六边形的边长为4,H为边AF的中点,则图中阴影部分的面积是 .
5.如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若点A的坐标为(﹣2,0),则点F的坐标为 .
6.如图,在正五边形ABCDE中,对角线BD与CE相交于点F,则∠BCE= .
十八.弧长的计算
1.如图,CD是半圆O的直径,点A,B是半圆上的两点,已知∠ABC=140°,CD=4,则AC的弧长为( )
A. B. C. D.
2.如图,△ABC内接⊙O,∠BAC=45°,BC,则的长是( )
A. B. C. D.π
3.如图,在正方形ABCD中,AB=2,连接AC,以点C为圆心、AC长为半径画弧,与BC的延长线交于点E,则图中的长为 .
十九.扇形面积的计算
1.如图,扇形OAB的半径为6cm,AC切于点A交OB的延长线于点C,若的长为3cm,AC=4cm,则图中阴影部分的面积为( )
A.1cm2 B.6cm2 C.4cm2 D.3cm2
2.已知扇形的圆心角为120°,半径为4cm,则扇形的面积是 cm2.
3.如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=3,
OC=1,分别连接AC、BD,则图中阴影部分的面积为( )
A.π B.π C.2π D.4π
4.如图,ABCD是围墙,AB∥CD,∠ABC=120°,一根6m长的绳子,一端拴在围墙一角的柱子B处,另一端E处拴着一只羊,这只羊活动区域的最大面积为 .
5.扇形的半径为2,圆心角为90°,则该扇形的面积(结果保留π)为 .
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2024/3/29 9:31:28;用户:初中数学;邮箱:18578317351;学号:27415165
一.圆的认识
1.某公园计划砌一个形状如图(1)所示的喷水池,后来有人建议改为图(2)的形状,且外圆的直径不变,喷水池边沿的宽度、高度不变,你认为砌喷水池的边沿( )
A.图(1)需要的材料多 B.图(2)需要的材料多
C.图(1)、图(2)需要的材料一样多 D.无法确定
二.垂径定理
1.如图,在⊙O中,弦AB=4,圆心O到AB的距离OC=1,则⊙O的半径长为( )
A.2 B.2 C. D.
2.已知⊙O的半径为5,点O到弦AB的距离为3,则⊙O上到弦AB所在直线的距离为2的点有( )
A.4个 B.3个 C.2个 D.1个
3.如图,⊙O的半径为6,将劣弧沿弦AB翻折,恰好经过圆心O,点C为优弧AB上的一个动点,则△ABC面积的最大值是( )
A. B. C. D.
4.下列说法中正确的个数有( )
①平分弦的直径一定垂直于弦;②圆是轴对称图形,每一条直径都是对称轴;③直径是弦;④长度相等的弧是等弧
A.1个 B.2个 C.3个 D.4个
5.如图,线段CD是⊙O的直径,CD⊥AB于点E,若AB长为16,OE长为6,则⊙O半径是( )
A.5 B.6 C.8 D.10
6.如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( )
A.3≤OM≤5 B.4≤OM≤5 C.3<OM<5 D.4<OM<5
三.垂径定理的应用
1.如图,武汉晴川桥可以近似地看作半径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB长度为300m,那么这些钢索中最长的一根为( )
A.50m B.45m C.40m D.60m
2.如图,某隧道的截面是一个半径为3.4米的半圆形,一辆宽3.2米的厢式卡车(截面是长方形)恰好能通过该隧道,则这辆卡车的高为多少米?
四.圆心角、弧、弦的关系
1.如图,在⊙O中,,A、C之间的距离为4,则线段BD= .
2.如图,已知AB是⊙O的直径,PA=PB,∠P=60°,则弧CD所对的圆心角等于 度.
五.圆周角定理
1.如图,点A、B、C在⊙O上,∠OBC=18°,则∠A=( )
A.18° B.36° C.72° D.144°
2.如图,AB是⊙O的直径,点C在⊙O上,半径OD∥AC,如果∠B=40°,那么∠BOD的度数为( )
A.120° B.130° C.140° D.150°
3.如图,BC是⊙O的弦,AD过圆心O,且AD⊥BC.若∠C=50°,则∠A的度数为( )
A.20° B.25° C.30° D.35°
4.如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则( )
A.3α+β=180° B.2α+β=180° C.3α﹣β=90° D.2α﹣β=90°
5.如图,⊙O为△ABC的外接圆,∠BAC=55°,则∠OBC的度数为( )
A.25° B.35° C.55° D.70°
6.如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则∠OBC的正弦值为( )
A. B. C. D.
7.如图,⊙O是△ABC的外接圆,已知∠ACO=30°,则∠B的度数是( )
A.30° B.45° C.60° D.75°
六.圆内接四边形的性质
1.如图,四边形ABCD内接于⊙O,AB=BC,连接OA、OB,∠BAO=70°,则∠D=( )
A.40° B.60° C.45° D.30°
2.如图,四边形ABCD内接于⊙O,AB是直径,OD∥BC,若∠C=124°,则∠B的度数为( )
A.56° B.68° C.72° D.78°
3.如图,四边形ABCD为⊙O的内接四边形,若四边形OBCD为菱形,则∠BAD的度数为( )
A.45° B.60° C.72° D.36°
4.如图,A,B,C,D是圆O上的四个点,点B是弧ABC的中点,如果∠ABC=72°,那么∠ADB= .
七.点与圆的位置关系
1.已知在平面直角坐标系中,P点坐标为(3,4),若以原点O为圆心,半径为5画圆,则点P与⊙O的位置关系是( )
A.点在圆内 B.点在圆上
C.点在圆外 D.不能确定
2.已知⊙O的半径为5,A为线段OP的中点,若OP=8,则点A与⊙O的位置关系是( )
A.点A在⊙O内 B.点A在⊙O上
C.点A在⊙O外 D.不确定
八.确定圆的条件
1.下列说法正确的是( )
A.三点确定一个圆
B.圆心角的度数等于圆周角的两倍
C.与半径垂直的直线是圆的切线
D.在同圆或等圆中,相等的圆周角所对的弦、弧分别相等
九.三角形的外接圆与外心
1.如图,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,⊙D经过A,B,O,C四点,∠ACO=120°,AB=4,则圆心点D的坐标是( )
A. B. C. D.
2.三角形的外心是三角形中( )
A.三条高的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
3.如图,△ABC内接于⊙O,AC是⊙O的直径,∠ACB=40°,点D是劣弧上一点,连接CD、BD,则∠D的度数是( )
A.50° B.45° C.140° D.130°
4.如图,O是△ABC的外心,则∠1+∠2+∠3=( )
A.60° B.75° C.90° D.105°
5.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,若AD=10,∠B=30°,则AC的长度为( )
A.3 B.4 C.5 D.10
十.直线与圆的位置关系
1.已知⊙O的半径为3,圆心O到直线l的距离为2,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
2.已知⊙O的半径为3cm,圆心O到直线l的距离是2cm,则直线l与⊙O的位置关系是 .
十一.切线的性质
1.如图,AB是⊙O的弦,AC是⊙O切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于( )
A.20° B.25° C.40° D.50°
2.如图,PA,PB分别与⊙O相切于A,B两点,∠P=72°,则∠C的度数为( )
A.36° B.54° C.72° D.108°
3.如图,菱形OABC的顶点A,B,C在⊙O上,过点B作⊙O的切线交OA的延长线于点D.若⊙O的半径为1,则BD的长为( )
A.1 B.2 C. D.
4.如图,AB是⊙O的直径,点C、D均在⊙O上,且AC平分∠DAB,过点C作⊙O的切线交AB的延长线于点P,连接BD.
(1)求证:BD∥CP;
(2)若sinP,BP=2,求BD的长.
5.如图,AB是半圆的直径,弦CD∥AB,过D点作圆O的切线DE,与AB延长线相交于点E,连接OC、AD,∠A=22.5°.
(1)求证:四边形COED是平行四边形;
(2)当CD=2时,求围成阴影部分图形的周长.
十二.切线的判定
1.如图,在△ABC中,AB=BC,CO平分∠ACB交AB于点O.当AC=CO时,以点O为圆心OA为半径作圆交AC于点D,过点D作DE⊥BC垂足为E.
(1)求∠B的度数;
(2)证明:DE是⊙O的切线.
十三.切线的判定与性质
1.如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;
(3)PO=AB;(4)∠PDB=120°.其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
十四.弦切角定理
1.如图,直线AB切⊙O于点A,割线BDC交⊙O于点D、C.若∠C=30°,∠B=20°,则∠ADC=( )
A.70° B.50° C.30° D.20°
十五.切割线定理
1.如图,从⊙O外一点A作⊙O的切线AB、AC,切点分别为B、C,且⊙O直径BD=6,连接CD、AO.
(1)求证:CD∥AO;
(2)设CD=x,AO=y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)若AO+CD=11,求AB的长.
十六.三角形的内切圆与内心
1.到三角形三条边的距离相等的点是三角形( )的交点.
A.三个内角平分线 B.三边垂直平分线
C.三条中线 D.三条高线
2.如图,△ABC中,∠ABC=50°,∠ACB=74°,点O是△ABC的内心.则∠BOC等于( )
A.124° B.118° C.112° D.62°
3.如图,⊙O的直径AB为10cm,弦BC为8cm,∠ACB的平分线交⊙O于点D,△ADB的内切圆半径是( )
A. B.5(1) C.5(1) D.
十七.正多边形和圆
1.若⊙O的内接正n边形的边长与⊙O的半径相等,则n的值为( )
A.4 B.5 C.6 D.7
2.已知圆的半径是2,则该圆的内接正六边形的面积是( )
A.3 B.9 C.18 D.36
3.如图,正六边形ABCDEF的边长为6,以顶点A为圆心,AB的长为半径画圆,则图中阴影部分的面积为( )
A.4π B.6π C.8π D.12π
4.如图,已知圆O的内接正六边形的边长为4,H为边AF的中点,则图中阴影部分的面积是 .
5.如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若点A的坐标为(﹣2,0),则点F的坐标为 .
6.如图,在正五边形ABCDE中,对角线BD与CE相交于点F,则∠BCE= .
十八.弧长的计算
1.如图,CD是半圆O的直径,点A,B是半圆上的两点,已知∠ABC=140°,CD=4,则AC的弧长为( )
A. B. C. D.
2.如图,△ABC内接⊙O,∠BAC=45°,BC,则的长是( )
A. B. C. D.π
3.如图,在正方形ABCD中,AB=2,连接AC,以点C为圆心、AC长为半径画弧,与BC的延长线交于点E,则图中的长为 .
十九.扇形面积的计算
1.如图,扇形OAB的半径为6cm,AC切于点A交OB的延长线于点C,若的长为3cm,AC=4cm,则图中阴影部分的面积为( )
A.1cm2 B.6cm2 C.4cm2 D.3cm2
2.已知扇形的圆心角为120°,半径为4cm,则扇形的面积是 cm2.
3.如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=3,
OC=1,分别连接AC、BD,则图中阴影部分的面积为( )
A.π B.π C.2π D.4π
4.如图,ABCD是围墙,AB∥CD,∠ABC=120°,一根6m长的绳子,一端拴在围墙一角的柱子B处,另一端E处拴着一只羊,这只羊活动区域的最大面积为 .
5.扇形的半径为2,圆心角为90°,则该扇形的面积(结果保留π)为 .
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2024/3/29 9:31:28;用户:初中数学;邮箱:18578317351;学号:27415165
