苏科版八年级数学上册试题 第5章 平面直角坐标系 章节复习卷(含答案)
文档属性
| 名称 | 苏科版八年级数学上册试题 第5章 平面直角坐标系 章节复习卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 312.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-23 21:53:25 | ||
图片预览




文档简介
第5章《平面直角坐标系》章节复习卷
一.选择题(每小题2分,共12分)
1.某同学的座位号为(2,4)那么该同学的位置是( )
A.第2排第4列 B.第4排第2列 C.第2列第4排 D.不好确定
2.将点A(3,2)沿x轴向左平移4个单位长度得到点A′,点A′关于y轴对称的点的坐标是( )
A.(﹣3,2) B.(﹣1,2) C.(1,2) D.(1,﹣2)
3.点P的坐标是(2-a,3a+6),且点P到两坐标轴的距离相等,则点P坐标是( )
A.(3, 3) B.(3,-3) C.(6,-6) D.(3,3)或
4.如图,直线m⊥n,在某平面直角坐标系中,x轴∥m,y轴∥n,点A的坐标为(-4,2),点B的坐标为(2,-4),则坐标原点为( )
A.O1 B.O2 C.O3 D.O4
5.如果P(a+b,ab)在第二象限,那么点Q (a,-b)在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.如下图所示,动点在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点,第2次运动到点,第3次运动到点,……,按照这样的运动规律,点第2021次运动到点( )
A. B. C. D.
二.填空题(每小题2分,共20分)
7.若点在y轴上,则点的坐标为_______.
8.在平面直角坐标系中,若A(1,4),B(3,2),将线段AB平移到CD,且C,D在坐标轴上,则C点坐标为________.
9.已知点 A(x,1)与点 B(2,y)关于 y 轴对称,则的值为__________.
10.若M(a,﹣b)在第二象限,则点N(ab,a+b)在第 象限.
11.如果P、Q两点坐标分别是(1,1),(-5,-3),那么线段PQ的中点坐标为________.
12.已知点A(0,1),B(0 ,2),点C在x轴上,且,则点C的坐标________.
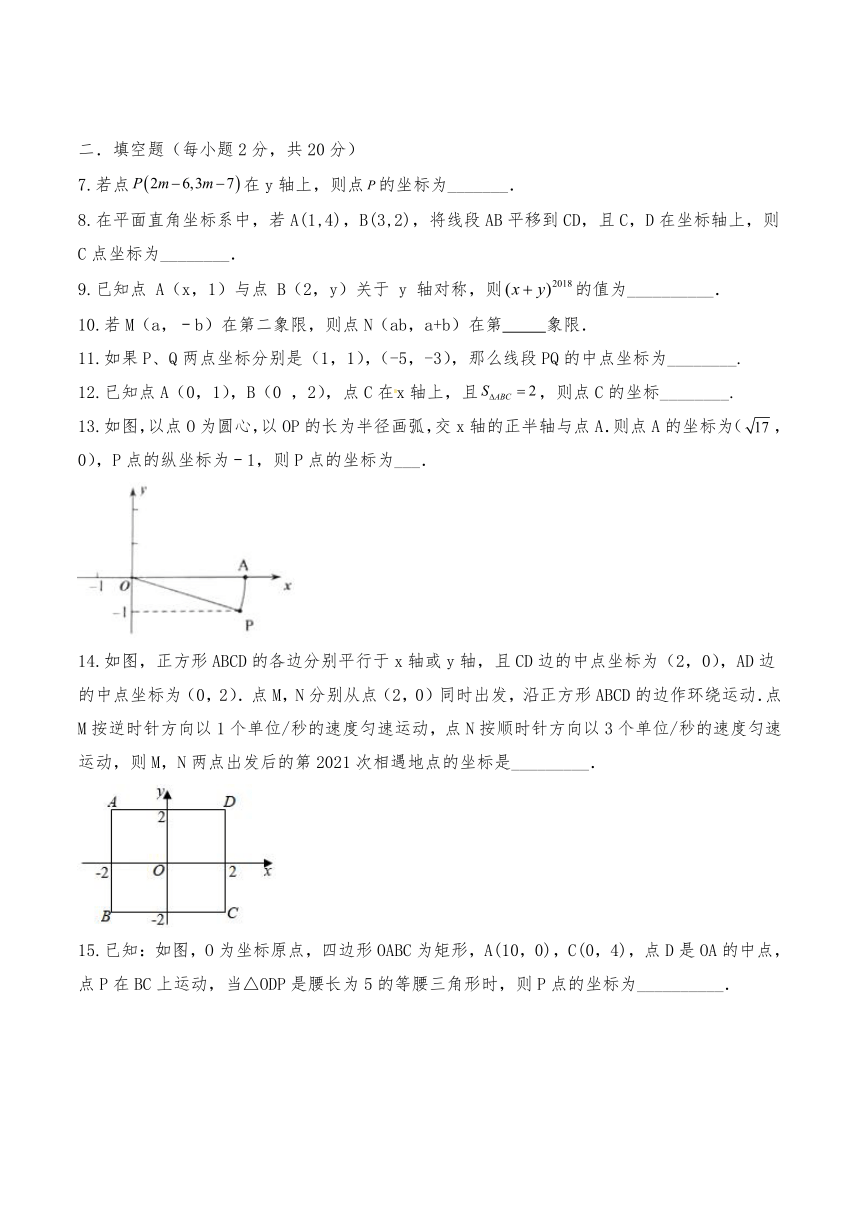
13.如图,以点O为圆心,以OP的长为半径画弧,交x轴的正半轴与点A.则点A的坐标为(,0),P点的纵坐标为﹣1,则P点的坐标为___.
14.如图,正方形ABCD的各边分别平行于x轴或y轴,且CD边的中点坐标为(2,0),AD边的中点坐标为(0,2).点M,N分别从点(2,0)同时出发,沿正方形ABCD的边作环绕运动.点M按逆时针方向以1个单位/秒的速度匀速运动,点N按顺时针方向以3个单位/秒的速度匀速运动,则M,N两点出发后的第2021次相遇地点的坐标是_________.
15.已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为__________.
16.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),……,按这样的运动规律,经过第2011次运动后,动点P的坐标是______.
三.解答题(共68分)
17.(8分)五子棋和象棋、围棋一样,深受广大棋友的喜爱,其规则是:15×15的正方形棋盘中,由黑方先行,轮流弈子,在任一方向上连成五子者为胜.如下图是两个五子棋爱好者甲和乙的对弈图;(甲执黑子先行,乙执白子后走),观察棋盘思考:若A点的位置记做(8,4),甲必须在哪个位置上落子,才不会让乙马上获胜.
18.(10分)已知点M(2a﹣5,a﹣1),分别根据下列条件求出点M的坐标.
(1)点N的坐标是(1,6),并且直线MN∥y轴;
(2)点M在第二象限,横坐标和纵坐标互为相反数.
19.(10分)如图,长方形ABCD在坐标平面内,点A的坐标是A(,1),且边AB,CD与x轴平行,边AD,BC与y轴平行,AB=4,AD=2.
(1)求B,C,D三点的坐标;
(2)怎样平移,才能使A点与原点O重合?
20.(10分)如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D、点B与点E、点C与点F分别是对应点.观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D、点B与点E、点C与点F的坐标,并说出三角形DEF是由三角形ABC经过怎样的变换得到的;
(2)若点Q(a+3,4-b)是点P(2a,2b-3)通过上述变换得到的,求a-b的值.
21.(10分)请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为(0,2),B点坐标为(﹣2,0);
(2)在x轴上画点C,使△ABC为等腰三角形,请画出所有符合条件的点C,并直接写出相应的C点坐标.
22.(10分)如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在, 求出点P的坐标,若不存在,请说明理由.
23.如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a﹣2|+(b﹣3)2=0.
(1)求a,b的值;
(2)如果在第二象限内有一点M(m,1),请用含m的式子表示四边形ABOM的面积;
(3)在(2)条件下,当m=﹣时,在坐标轴的负半轴上是否存在点N,使得四边形ABOM的面积与△ABN的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
答案
一.选择题
1.D
【解析】解:题中没有规定排在前,列在后;还是列在前,排在后,
因此无法确定该同学的所坐位置.
故选D.
2.C
【解析】根据坐标的平移变化的规律,左右平移只改变点的横坐标,左减右加.上下平移只改变点的纵坐标,下减上加,因此,将点A(3,2)沿x轴向左平移4个单位长度得到点A′,点A′的坐标为(-1,2).关于y轴对称的点的坐标特征是纵坐标不变,横坐标互为相反数,从而点A′(-1,2)关于y轴对称的点的坐标是(1,2).
故选C.
3.D
【解析】解: 点P到两坐标轴的距离相等,
或
当时,
当
综上:的坐标为:或
故选D.
4.A
【解析】因为A点坐标为(-4,2),所以,原点在点A的右边,也在点A的下边2个单位处,从点B来看,B(2,-4),所以,原点在点B的左边,且在点B的上边4个单位处.如下图,O1符合.
5.B
【解析】∵P(a+b,ab)在第二象限,
∴a+b<0,ab>0,∴a<0,b<0,∴-b>0,∴点Q(a,-b)在第二象限.
故选B.
6.A
【解析】解:令P点第n次运动到的点为Pn点(n为自然数).
观察,发现规律:P0(0,0),P1(1,1),P2(2,0),P3(3, 1),P4(4,0),P5(5,1),…,
∴P4n(4n,0),P4n+1(4n+1,1),P4n+2(4n+2,0),P4n+3(4n+3, 1).
∵2021=505×4+1,
∴P第2021次运动到点(2021,1).
故选:A.
二.填空题
7.(0,2)
【解析】解:∵点在y轴上,
∴,∴,∴,∴点的坐标为(0,2);
故答案为:(0,2).
8.(0,2)或(-2,0)
,将线段AB平移到CD,且C,D在坐标轴上,
∴平移的方法是向左平移1个单位,向下平移2个单位,
∴C点为(0,2),
继续向左平移2个单位,向下平移2个单位,
则C点坐标为(-2,0).
综上,C点坐标为(0,2)或(-2,0).
故答案为:(0,2)或(-2,0).
9.1
【解析】解:∵点A(x,1)与点B(2,y)关于y轴对称,
∴x=-2,y=1,∴(x+y)2018=1,
故答案为1.
10.四
【解析】∵点P(a,-b)在第二象限,
∴a<0,b<0,
∴ab>0,a+b<0,
∴点Q(ab,a+b)在第四象限,故填:四.
11.(-2,-1)
【解析】解:中点的横坐标为: =-2,纵坐标为:=-1,即线段PQ的中点坐标为(-2,-1).
故答案为(-2,-1).
12.(4,0)或(﹣4,0)
【解析】设C点坐标为(|x|,0)
∴
解得:x=±4
所以,点C的坐标为(4,0)或(-4,0).
13.(4, 1).
【解析】解:如图,OP=OA=,
在直角△OBP中,OP=,OB=1,
由勾股定理知:BP=.
则P(4, 1).
故答案是:(4, 1).
14.(0,2).
【解析】解:由已知,正方形周长为16,
∵M、N速度分别为1单位/秒,3单位/秒,
则两个物体每次相遇时间间隔为=4秒,
则两个物体相遇点依次为(0,2)、(﹣2,0)、(0,﹣2)、(2,0)
∵2021=4×505…1,
∴第2021次两个物体相遇位置为(0,2),
故答案为:(0,2).
15.P(3,4)或(2,4)或(8,4)
【解析】由题意,当△ODP是腰长为5的等腰三角形时,有三种情况:
(1)如图所示,PD=OD=5,点P在点D的左侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE=,
∴OE=OD -DE=5-3=2,
∴此时点P坐标为(2,4);
(2)如图所示,OP=OD=5.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△POE中,由勾股定理得: OE=,
∴此时点P坐标为(3,4);
(3)如图所示,PD=OD=5,点P在点D的右侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得: DE=,
∴OE=OD+DE=5+3=8,
∴此时点P坐标为(8,4).
综上所述,点P的坐标为:(2,4)或(3,4)或(8,4).
16.(2011,2)
【解析】根据已知提供的数据从横纵坐标分别分析得出横坐标为运动次数,纵坐标为1,0,2,0,每4次一轮这一规律,进而求出即可.
根据动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),
第2次接着运动到点(2,0),第3次接着运动到点(3,2),
∴第4次运动到点(4,0),第5次接着运动到点(5,1),…,
∴横坐标为运动次数,经过第2011次运动后,动点P的横坐标为2011,
纵坐标为1,0,2,0,每4次一轮,
∴经过第2011次运动后,动点P的纵坐标为:2011÷4=502余3,
故纵坐标为四个数中第三个,即为2,
∴经过第2011次运动后,动点P的坐标是:(2011,2),
故答案为(2011,2).
三.解答题
17.∵白棋已经有三个在一条直线上,
∴甲必须在(5,3)或(1,7)位置上落子,才不会让乙马上获胜.
18.解:(1)∵直线MN∥y轴,
∴2a﹣5=1,解得a=3,∴a﹣1=3﹣1=2,
∴点M的坐标为(1,2);
(2)∵横坐标和纵坐标互为相反数,∴2a﹣5+a﹣1=0,
解得a=2,∴2a﹣5=2×2﹣5=﹣1,a﹣1=2﹣1=1,
∴点M的坐标为(﹣1,1).
19.(1)∵A(,1),AB=4,AD=2,
∴BC到y轴的距离为4+, CD到x轴的距离2+1=3,
∴点B的坐标为(4+,1),点C的坐标为(4+,3),点D的坐标为(,3);
(2)由图可知,先向下平移1个单位长度,再向左平移个单位长度(或先向左平移个单位长度,再向下平移1个单位长度).
20.(1)A(2,4),D(-1,1),B(1,2),E(-2,-1),C(4,1),F(1,-2);
三角形DEF是由三角形ABC先向左平移3个单位,再向下平移3个单位得到的(或先向下平移3个单位,再向左平移3个单位得到的).
(2)由题意得2a-3=a+3,2b-3-3=4-b,
解得a=6,b=,
∴a-b=6-=.
21.(1)在网格中建立平面直角坐标系如图所示:
(2)满足条件的点有4个:C1:(2,0);C2:(2 2,0);C3:(0,0);C4:( 2 2,0).
22.(1)由已知,
可得:a=2,b=3,c=4;
(2)∵S△ABO=×2×3=3,S△APO=×2×(-m)=-m,
∴S四边形ABOP=S△ABO+S△APO=3+(-m)=3-m
(3)因为S△ABC=×4×3=6,
∵S四边形ABOP=S△ABC
∴3-m=6,
则m=-3,
所以存在点P(-3, )使S四边形ABOP=S△ABC.
23.(1)、∵a,b满足|a﹣2|+(b﹣3)2=0, ∴a﹣2=0,b﹣3=0,
解得a=2,b=3;
(2)、过点M作MN丄y轴于点N.
四边形AMOB面积=S△AMO+S△AOB=MN OA+OA OB=×(﹣m)×2+×2×3=﹣m+3;
(3)当m=﹣时,四边形ABOM的面积=4.5. ∴S△ABN=4.5,
①当N在x轴负半轴上时,
设N(x,0),则S△ABN=AO NB=×2×(3﹣x)=4.5, 解得x=﹣1.5;
②当N在y轴负半轴上时,设N(0,y),则
S△ABN=BO AN=×3×(2﹣y)=4.5, 解得y=﹣1.
∴N(0,﹣1)或N(﹣1.5,0).
一.选择题(每小题2分,共12分)
1.某同学的座位号为(2,4)那么该同学的位置是( )
A.第2排第4列 B.第4排第2列 C.第2列第4排 D.不好确定
2.将点A(3,2)沿x轴向左平移4个单位长度得到点A′,点A′关于y轴对称的点的坐标是( )
A.(﹣3,2) B.(﹣1,2) C.(1,2) D.(1,﹣2)
3.点P的坐标是(2-a,3a+6),且点P到两坐标轴的距离相等,则点P坐标是( )
A.(3, 3) B.(3,-3) C.(6,-6) D.(3,3)或
4.如图,直线m⊥n,在某平面直角坐标系中,x轴∥m,y轴∥n,点A的坐标为(-4,2),点B的坐标为(2,-4),则坐标原点为( )
A.O1 B.O2 C.O3 D.O4
5.如果P(a+b,ab)在第二象限,那么点Q (a,-b)在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.如下图所示,动点在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点,第2次运动到点,第3次运动到点,……,按照这样的运动规律,点第2021次运动到点( )
A. B. C. D.
二.填空题(每小题2分,共20分)
7.若点在y轴上,则点的坐标为_______.
8.在平面直角坐标系中,若A(1,4),B(3,2),将线段AB平移到CD,且C,D在坐标轴上,则C点坐标为________.
9.已知点 A(x,1)与点 B(2,y)关于 y 轴对称,则的值为__________.
10.若M(a,﹣b)在第二象限,则点N(ab,a+b)在第 象限.
11.如果P、Q两点坐标分别是(1,1),(-5,-3),那么线段PQ的中点坐标为________.
12.已知点A(0,1),B(0 ,2),点C在x轴上,且,则点C的坐标________.
13.如图,以点O为圆心,以OP的长为半径画弧,交x轴的正半轴与点A.则点A的坐标为(,0),P点的纵坐标为﹣1,则P点的坐标为___.
14.如图,正方形ABCD的各边分别平行于x轴或y轴,且CD边的中点坐标为(2,0),AD边的中点坐标为(0,2).点M,N分别从点(2,0)同时出发,沿正方形ABCD的边作环绕运动.点M按逆时针方向以1个单位/秒的速度匀速运动,点N按顺时针方向以3个单位/秒的速度匀速运动,则M,N两点出发后的第2021次相遇地点的坐标是_________.
15.已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为__________.
16.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),……,按这样的运动规律,经过第2011次运动后,动点P的坐标是______.
三.解答题(共68分)
17.(8分)五子棋和象棋、围棋一样,深受广大棋友的喜爱,其规则是:15×15的正方形棋盘中,由黑方先行,轮流弈子,在任一方向上连成五子者为胜.如下图是两个五子棋爱好者甲和乙的对弈图;(甲执黑子先行,乙执白子后走),观察棋盘思考:若A点的位置记做(8,4),甲必须在哪个位置上落子,才不会让乙马上获胜.
18.(10分)已知点M(2a﹣5,a﹣1),分别根据下列条件求出点M的坐标.
(1)点N的坐标是(1,6),并且直线MN∥y轴;
(2)点M在第二象限,横坐标和纵坐标互为相反数.
19.(10分)如图,长方形ABCD在坐标平面内,点A的坐标是A(,1),且边AB,CD与x轴平行,边AD,BC与y轴平行,AB=4,AD=2.
(1)求B,C,D三点的坐标;
(2)怎样平移,才能使A点与原点O重合?
20.(10分)如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D、点B与点E、点C与点F分别是对应点.观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D、点B与点E、点C与点F的坐标,并说出三角形DEF是由三角形ABC经过怎样的变换得到的;
(2)若点Q(a+3,4-b)是点P(2a,2b-3)通过上述变换得到的,求a-b的值.
21.(10分)请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为(0,2),B点坐标为(﹣2,0);
(2)在x轴上画点C,使△ABC为等腰三角形,请画出所有符合条件的点C,并直接写出相应的C点坐标.
22.(10分)如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在, 求出点P的坐标,若不存在,请说明理由.
23.如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a﹣2|+(b﹣3)2=0.
(1)求a,b的值;
(2)如果在第二象限内有一点M(m,1),请用含m的式子表示四边形ABOM的面积;
(3)在(2)条件下,当m=﹣时,在坐标轴的负半轴上是否存在点N,使得四边形ABOM的面积与△ABN的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
答案
一.选择题
1.D
【解析】解:题中没有规定排在前,列在后;还是列在前,排在后,
因此无法确定该同学的所坐位置.
故选D.
2.C
【解析】根据坐标的平移变化的规律,左右平移只改变点的横坐标,左减右加.上下平移只改变点的纵坐标,下减上加,因此,将点A(3,2)沿x轴向左平移4个单位长度得到点A′,点A′的坐标为(-1,2).关于y轴对称的点的坐标特征是纵坐标不变,横坐标互为相反数,从而点A′(-1,2)关于y轴对称的点的坐标是(1,2).
故选C.
3.D
【解析】解: 点P到两坐标轴的距离相等,
或
当时,
当
综上:的坐标为:或
故选D.
4.A
【解析】因为A点坐标为(-4,2),所以,原点在点A的右边,也在点A的下边2个单位处,从点B来看,B(2,-4),所以,原点在点B的左边,且在点B的上边4个单位处.如下图,O1符合.
5.B
【解析】∵P(a+b,ab)在第二象限,
∴a+b<0,ab>0,∴a<0,b<0,∴-b>0,∴点Q(a,-b)在第二象限.
故选B.
6.A
【解析】解:令P点第n次运动到的点为Pn点(n为自然数).
观察,发现规律:P0(0,0),P1(1,1),P2(2,0),P3(3, 1),P4(4,0),P5(5,1),…,
∴P4n(4n,0),P4n+1(4n+1,1),P4n+2(4n+2,0),P4n+3(4n+3, 1).
∵2021=505×4+1,
∴P第2021次运动到点(2021,1).
故选:A.
二.填空题
7.(0,2)
【解析】解:∵点在y轴上,
∴,∴,∴,∴点的坐标为(0,2);
故答案为:(0,2).
8.(0,2)或(-2,0)
,将线段AB平移到CD,且C,D在坐标轴上,
∴平移的方法是向左平移1个单位,向下平移2个单位,
∴C点为(0,2),
继续向左平移2个单位,向下平移2个单位,
则C点坐标为(-2,0).
综上,C点坐标为(0,2)或(-2,0).
故答案为:(0,2)或(-2,0).
9.1
【解析】解:∵点A(x,1)与点B(2,y)关于y轴对称,
∴x=-2,y=1,∴(x+y)2018=1,
故答案为1.
10.四
【解析】∵点P(a,-b)在第二象限,
∴a<0,b<0,
∴ab>0,a+b<0,
∴点Q(ab,a+b)在第四象限,故填:四.
11.(-2,-1)
【解析】解:中点的横坐标为: =-2,纵坐标为:=-1,即线段PQ的中点坐标为(-2,-1).
故答案为(-2,-1).
12.(4,0)或(﹣4,0)
【解析】设C点坐标为(|x|,0)
∴
解得:x=±4
所以,点C的坐标为(4,0)或(-4,0).
13.(4, 1).
【解析】解:如图,OP=OA=,
在直角△OBP中,OP=,OB=1,
由勾股定理知:BP=.
则P(4, 1).
故答案是:(4, 1).
14.(0,2).
【解析】解:由已知,正方形周长为16,
∵M、N速度分别为1单位/秒,3单位/秒,
则两个物体每次相遇时间间隔为=4秒,
则两个物体相遇点依次为(0,2)、(﹣2,0)、(0,﹣2)、(2,0)
∵2021=4×505…1,
∴第2021次两个物体相遇位置为(0,2),
故答案为:(0,2).
15.P(3,4)或(2,4)或(8,4)
【解析】由题意,当△ODP是腰长为5的等腰三角形时,有三种情况:
(1)如图所示,PD=OD=5,点P在点D的左侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE=,
∴OE=OD -DE=5-3=2,
∴此时点P坐标为(2,4);
(2)如图所示,OP=OD=5.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△POE中,由勾股定理得: OE=,
∴此时点P坐标为(3,4);
(3)如图所示,PD=OD=5,点P在点D的右侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得: DE=,
∴OE=OD+DE=5+3=8,
∴此时点P坐标为(8,4).
综上所述,点P的坐标为:(2,4)或(3,4)或(8,4).
16.(2011,2)
【解析】根据已知提供的数据从横纵坐标分别分析得出横坐标为运动次数,纵坐标为1,0,2,0,每4次一轮这一规律,进而求出即可.
根据动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),
第2次接着运动到点(2,0),第3次接着运动到点(3,2),
∴第4次运动到点(4,0),第5次接着运动到点(5,1),…,
∴横坐标为运动次数,经过第2011次运动后,动点P的横坐标为2011,
纵坐标为1,0,2,0,每4次一轮,
∴经过第2011次运动后,动点P的纵坐标为:2011÷4=502余3,
故纵坐标为四个数中第三个,即为2,
∴经过第2011次运动后,动点P的坐标是:(2011,2),
故答案为(2011,2).
三.解答题
17.∵白棋已经有三个在一条直线上,
∴甲必须在(5,3)或(1,7)位置上落子,才不会让乙马上获胜.
18.解:(1)∵直线MN∥y轴,
∴2a﹣5=1,解得a=3,∴a﹣1=3﹣1=2,
∴点M的坐标为(1,2);
(2)∵横坐标和纵坐标互为相反数,∴2a﹣5+a﹣1=0,
解得a=2,∴2a﹣5=2×2﹣5=﹣1,a﹣1=2﹣1=1,
∴点M的坐标为(﹣1,1).
19.(1)∵A(,1),AB=4,AD=2,
∴BC到y轴的距离为4+, CD到x轴的距离2+1=3,
∴点B的坐标为(4+,1),点C的坐标为(4+,3),点D的坐标为(,3);
(2)由图可知,先向下平移1个单位长度,再向左平移个单位长度(或先向左平移个单位长度,再向下平移1个单位长度).
20.(1)A(2,4),D(-1,1),B(1,2),E(-2,-1),C(4,1),F(1,-2);
三角形DEF是由三角形ABC先向左平移3个单位,再向下平移3个单位得到的(或先向下平移3个单位,再向左平移3个单位得到的).
(2)由题意得2a-3=a+3,2b-3-3=4-b,
解得a=6,b=,
∴a-b=6-=.
21.(1)在网格中建立平面直角坐标系如图所示:
(2)满足条件的点有4个:C1:(2,0);C2:(2 2,0);C3:(0,0);C4:( 2 2,0).
22.(1)由已知,
可得:a=2,b=3,c=4;
(2)∵S△ABO=×2×3=3,S△APO=×2×(-m)=-m,
∴S四边形ABOP=S△ABO+S△APO=3+(-m)=3-m
(3)因为S△ABC=×4×3=6,
∵S四边形ABOP=S△ABC
∴3-m=6,
则m=-3,
所以存在点P(-3, )使S四边形ABOP=S△ABC.
23.(1)、∵a,b满足|a﹣2|+(b﹣3)2=0, ∴a﹣2=0,b﹣3=0,
解得a=2,b=3;
(2)、过点M作MN丄y轴于点N.
四边形AMOB面积=S△AMO+S△AOB=MN OA+OA OB=×(﹣m)×2+×2×3=﹣m+3;
(3)当m=﹣时,四边形ABOM的面积=4.5. ∴S△ABN=4.5,
①当N在x轴负半轴上时,
设N(x,0),则S△ABN=AO NB=×2×(3﹣x)=4.5, 解得x=﹣1.5;
②当N在y轴负半轴上时,设N(0,y),则
S△ABN=BO AN=×3×(2﹣y)=4.5, 解得y=﹣1.
∴N(0,﹣1)或N(﹣1.5,0).
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
