浙江省玉环县龙岩中学人教版八年级数学下册17.1勾股定理课件(共34张PPT)
文档属性
| 名称 | 浙江省玉环县龙岩中学人教版八年级数学下册17.1勾股定理课件(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-31 00:00:00 | ||
图片预览






文档简介
课件34张PPT。17.1勾股定理——数形结合之美发明千千万
起点是一问发现定理
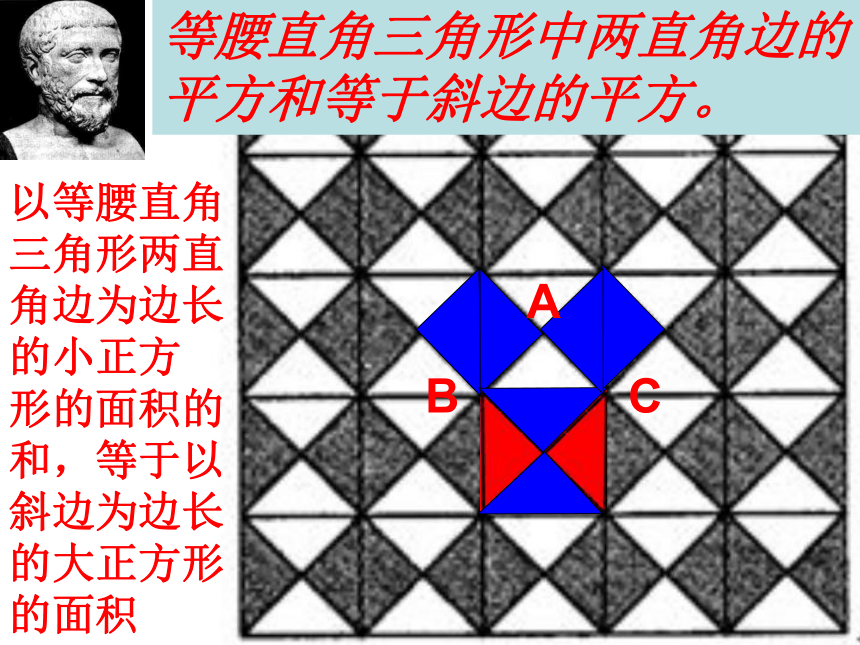
毕达格拉斯定理 毕达哥拉斯有次应邀参加一位富有政要的餐会,这位主人豪华宫殿般的餐厅铺着是正方形美丽的大理石地砖,由于大餐迟迟不上桌,这些饥肠辘辘的贵宾颇有怨言;但这位善于观察和理解的数学家却凝视脚下这些排列规则、美丽的方形磁砖,但毕达哥拉斯不只是欣赏磁砖的美丽,而是想到它们和[数]之间的关系,于是 拿了画笔并且蹲在地板上,选了一块磁砖以它的对角线 AB为边画一个正方形,他发现这个正方形面积恰好等于两块磁砖的面积和。他很好奇.... 于是再以两块磁砖拼成的矩形之对角线作另一个正方形,他发现这个正方形之面积等于5块磁砖的面积,也就是以两股为边作正方形面积之和。至此毕达哥拉斯作了大胆的假设: 任何直角三角形,其斜边的平方恰好等于另两边平方之和。那一顿饭,这位古希腊数学大师,视线都一直没有离开地面。 ABC以等腰直角三角形两直角边为边长的小正方
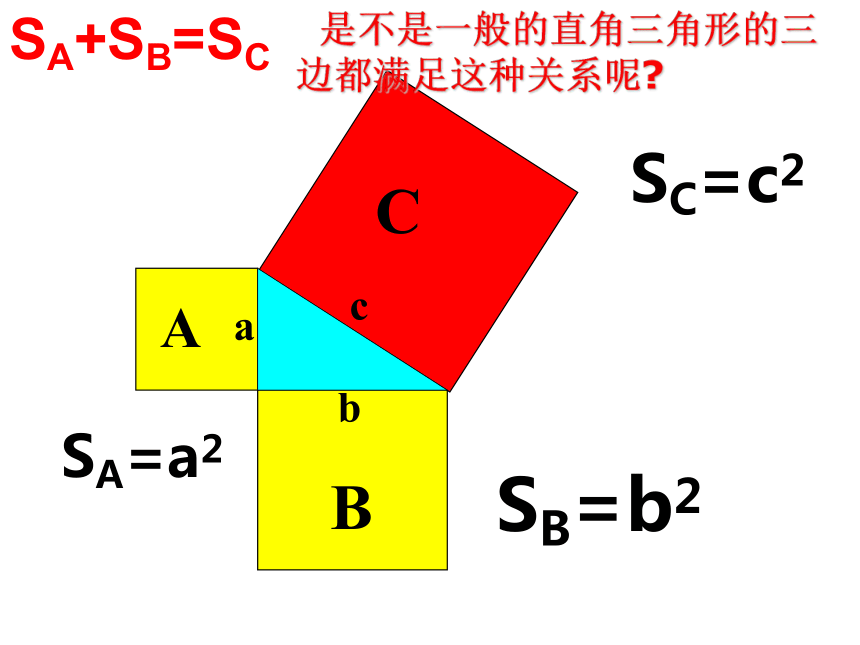
形的面积的和,等于以斜边为边长的大正方形的面积等腰直角三角形中两直角边的平方和等于斜边的平方。ABCSA=a2SB=b2SC=c2abcSA+SB=SC 是不是一般的直角三角形的三边都满足这种关系呢?
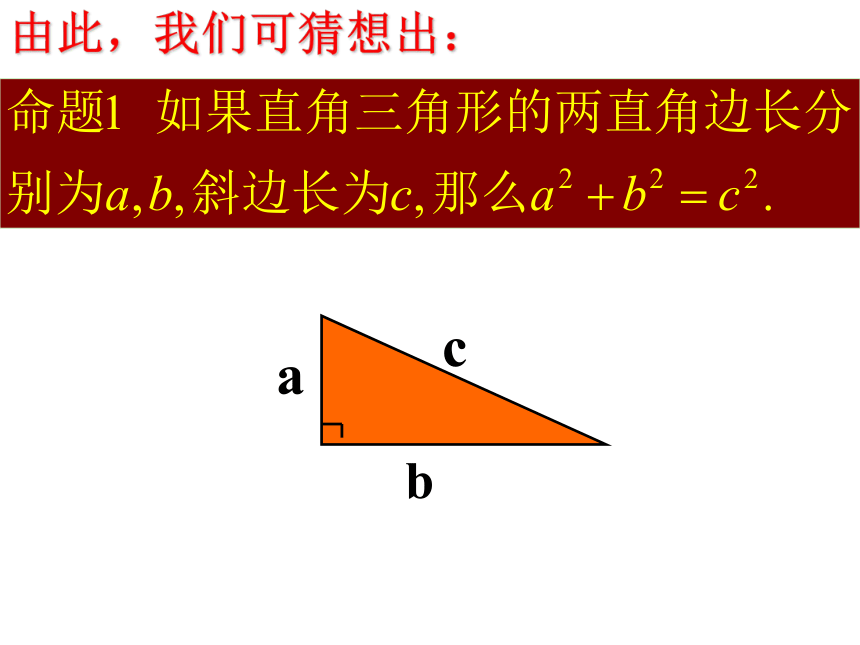
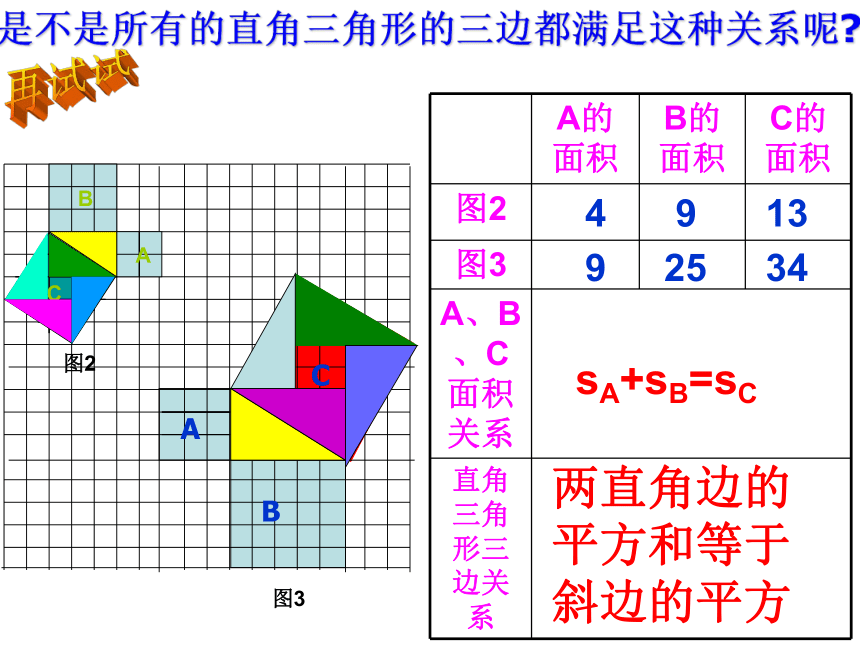
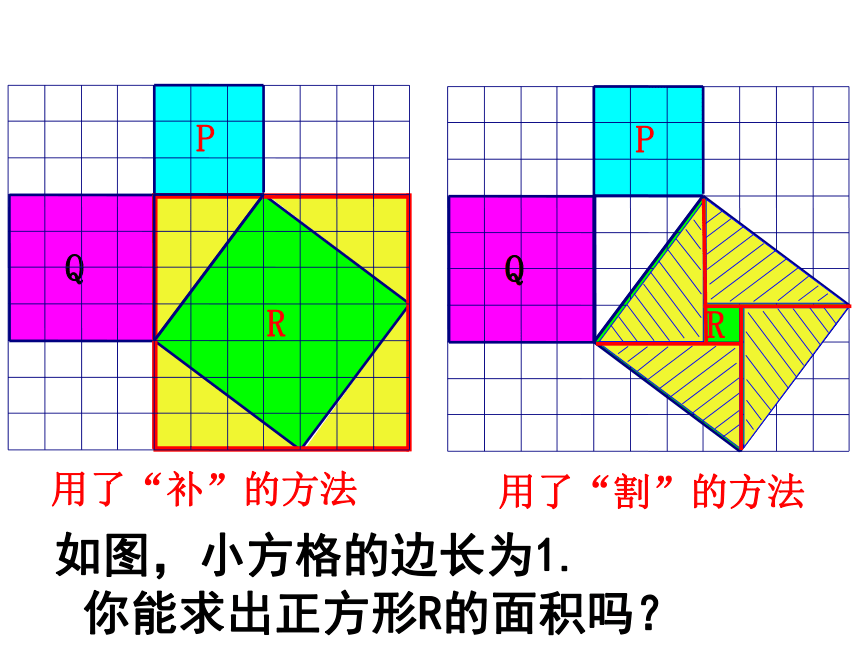
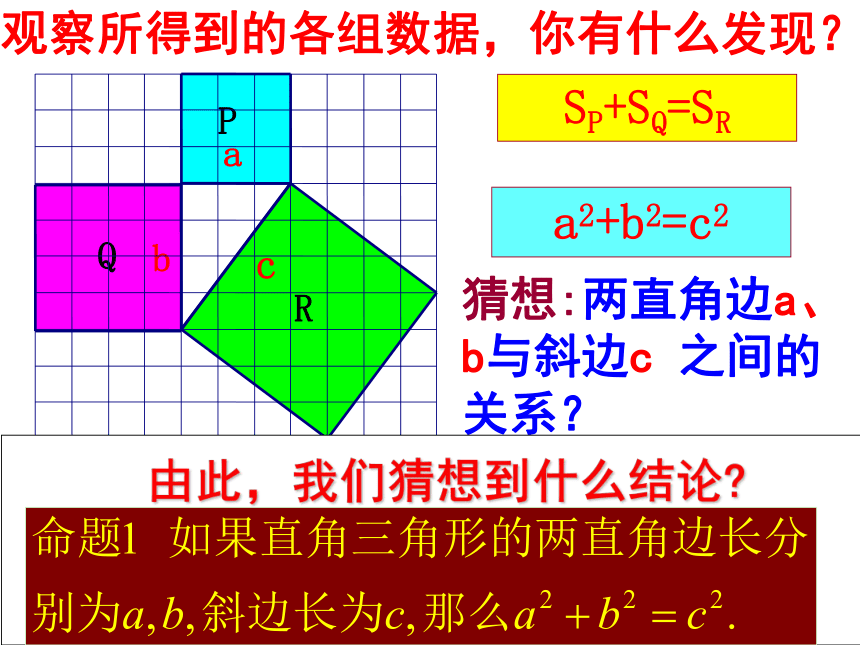
由此,我们可猜想出:abc证明定理ABC图2图3491392534sA+sB=sC两直角边的平方和等于斜边的平方ABC再试试是不是所有的直角三角形的三边都满足这种关系呢?C如图,小方格的边长为1.(1)你能求出正方形R的面积吗?用了“补”的方法用了“割”的方法QacbSP+SQ=SR 观察所得到的各组数据,你有什么发现?猜想:两直角边a、b与斜边c 之间的关系?a2+b2=c2由此,我们猜想到什么结论?大正方形面积:还可看作四个直角三角形和一个小正方形之和:即:经过证明被确认正确的命题叫做定理.证明方法1:证明方法2:证明方法3:又比较两式可知:a2+b2=c2如果直角三角形两直角边分别为a,b,斜边为c,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方.勾股定理勾股弦在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.勾 股 世 界 在西方,因为是毕达哥拉斯最先发现这个定理的,所以西方人通常称勾股定理为“毕达哥拉斯定理” .传说毕达哥拉斯证明这个定理之后,杀了一百头牛来庆祝,所以它又叫“百牛定理” .在欧洲中世纪它又被戏称为“驴桥定理” ,因为那时数学水平较低,很多人学习勾股定理时被卡住,难以理解和接受。所以勾股定理被戏称为“驴桥”,意谓笨蛋的难关 。 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就曾提出, “勾三、股四、弦五”,所以勾股定理又叫“商高定理”小组合作,探究证明方法用赵爽弦图证明命题1=证法一:“赵爽弦图”.达芬奇与勾股定理 意大利文艺复兴时代的著名画家达芬奇也深深的沉醉在勾股定理的魅力中。17.1勾股定理——数形结合之美P24
1、2熟悉定理1.设直角三角形的两条直角边长分别为a和b,斜边长为c2013864abc练习结论变形2.如图,图中所有的三角形都是直角三角形,所有的四边形都是正方形,已知正方形A,B,C,D的边长分别为12,16,9,12,求最大正方形E的面积。625求最大正方形的边长?253.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为___________cm2。49变式训练美丽的勾股树在直线上依次摆着7个正方形(如图),已知倾斜放置的3个正方形的面积分别为1,2,3,水平放置的4个正方形的面积是S1,S2,S3,S4,
则S1+S2+S3+S4=______.4、如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积。Dx14-x4、在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和腰上高长度ABCD131310H提示:利用面积相等的关系如图,你能求出S1、S2、S3之间的关系式吗?? 合作探究2 以直角三角形三边为边作等边三角形,这3个等边三角形的面积之间有什么关系?? 合作探究3本节课你学到了什么?感悟与反思┏a2+b2=c2acb 定理内容:直角三角形两直角边的平方和等于斜边的平方.勾股弦人类最伟大的十个科学发现之一 .
勾股定理: 课堂小结勾股
定理
形的面积的和,等于以斜边为边长的大正方形的面积等腰直角三角形中两直角边的平方和等于斜边的平方。ABCSA=a2SB=b2SC=c2abcSA+SB=SC 是不是一般的直角三角形的三边都满足这种关系呢?
由此,我们可猜想出:abc证明定理ABC图2图3491392534sA+sB=sC两直角边的平方和等于斜边的平方ABC再试试是不是所有的直角三角形的三边都满足这种关系呢?C如图,小方格的边长为1.(1)你能求出正方形R的面积吗?用了“补”的方法用了“割”的方法QacbSP+SQ=SR 观察所得到的各组数据,你有什么发现?猜想:两直角边a、b与斜边c 之间的关系?a2+b2=c2由此,我们猜想到什么结论?大正方形面积:还可看作四个直角三角形和一个小正方形之和:即:经过证明被确认正确的命题叫做定理.证明方法1:证明方法2:证明方法3:又比较两式可知:a2+b2=c2如果直角三角形两直角边分别为a,b,斜边为c,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方.勾股定理勾股弦在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.勾 股 世 界 在西方,因为是毕达哥拉斯最先发现这个定理的,所以西方人通常称勾股定理为“毕达哥拉斯定理” .传说毕达哥拉斯证明这个定理之后,杀了一百头牛来庆祝,所以它又叫“百牛定理” .在欧洲中世纪它又被戏称为“驴桥定理” ,因为那时数学水平较低,很多人学习勾股定理时被卡住,难以理解和接受。所以勾股定理被戏称为“驴桥”,意谓笨蛋的难关 。 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就曾提出, “勾三、股四、弦五”,所以勾股定理又叫“商高定理”小组合作,探究证明方法用赵爽弦图证明命题1=证法一:“赵爽弦图”.达芬奇与勾股定理 意大利文艺复兴时代的著名画家达芬奇也深深的沉醉在勾股定理的魅力中。17.1勾股定理——数形结合之美P24
1、2熟悉定理1.设直角三角形的两条直角边长分别为a和b,斜边长为c2013864abc练习结论变形2.如图,图中所有的三角形都是直角三角形,所有的四边形都是正方形,已知正方形A,B,C,D的边长分别为12,16,9,12,求最大正方形E的面积。625求最大正方形的边长?253.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为___________cm2。49变式训练美丽的勾股树在直线上依次摆着7个正方形(如图),已知倾斜放置的3个正方形的面积分别为1,2,3,水平放置的4个正方形的面积是S1,S2,S3,S4,
则S1+S2+S3+S4=______.4、如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积。Dx14-x4、在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和腰上高长度ABCD131310H提示:利用面积相等的关系如图,你能求出S1、S2、S3之间的关系式吗?? 合作探究2 以直角三角形三边为边作等边三角形,这3个等边三角形的面积之间有什么关系?? 合作探究3本节课你学到了什么?感悟与反思┏a2+b2=c2acb 定理内容:直角三角形两直角边的平方和等于斜边的平方.勾股弦人类最伟大的十个科学发现之一 .
勾股定理: 课堂小结勾股
定理
