第二十五章 概率初步质量评估题 2024-2025学年人教版数学九年级上册(含答案)
文档属性
| 名称 | 第二十五章 概率初步质量评估题 2024-2025学年人教版数学九年级上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 227.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-23 00:00:00 | ||
图片预览


文档简介
第二十五章 概率初步质量评估
[时间:90分钟 分值:150分]
一、选择题(共12小题,每小题3分,共36分)
1.下列所给的事件中,是必然事件的是( )
A.买10注福利彩票会中奖
B.某校的400名学生中,至少有2名学生的生日是同一天
C.连续4次投掷质地均匀的硬币,会有1次硬币正面朝上
D.2024年的春节假期成都会下雪
2.成语是中华文化的瑰宝,是中华文化的微缩景观.下列成语:①水中捞月;②守株待兔;③百步穿杨;④瓮中捉鳖.描述的事件是不可能事件的是( )
A.① B.② C.③ D.④
3.[2022·临海]某路口红绿灯的时间设置如下:绿灯60秒,红灯40秒,黄灯3秒.当车随机经过该路口,遇到哪一种灯的可能性最大( )
A.绿灯 B.红灯 C.黄灯 D.不能确定
4.一个纸箱中装有白色和黄色两种乒乓球,共20个,这些球除颜色外都相同,将球搅匀,每次从中随机摸出一个球,记下颜色后放回、搅匀再摸球,通过大量重复摸球试验后,将摸到白球的频率绘制成如图所示的统计图,由此可估计纸箱中白球的个数为( )
第4题图
A.4 B.6 C.8 D.10
5.[2023·瑞安]如图,某展览大厅有A,B两个入口,C,D,E三个出口,小明任选一个入口进入展览大厅,参观结束后任选一个出口离开,不同的出入路线一共有( )
第5题图
A.3种 B.4种 C.5种 D.6种
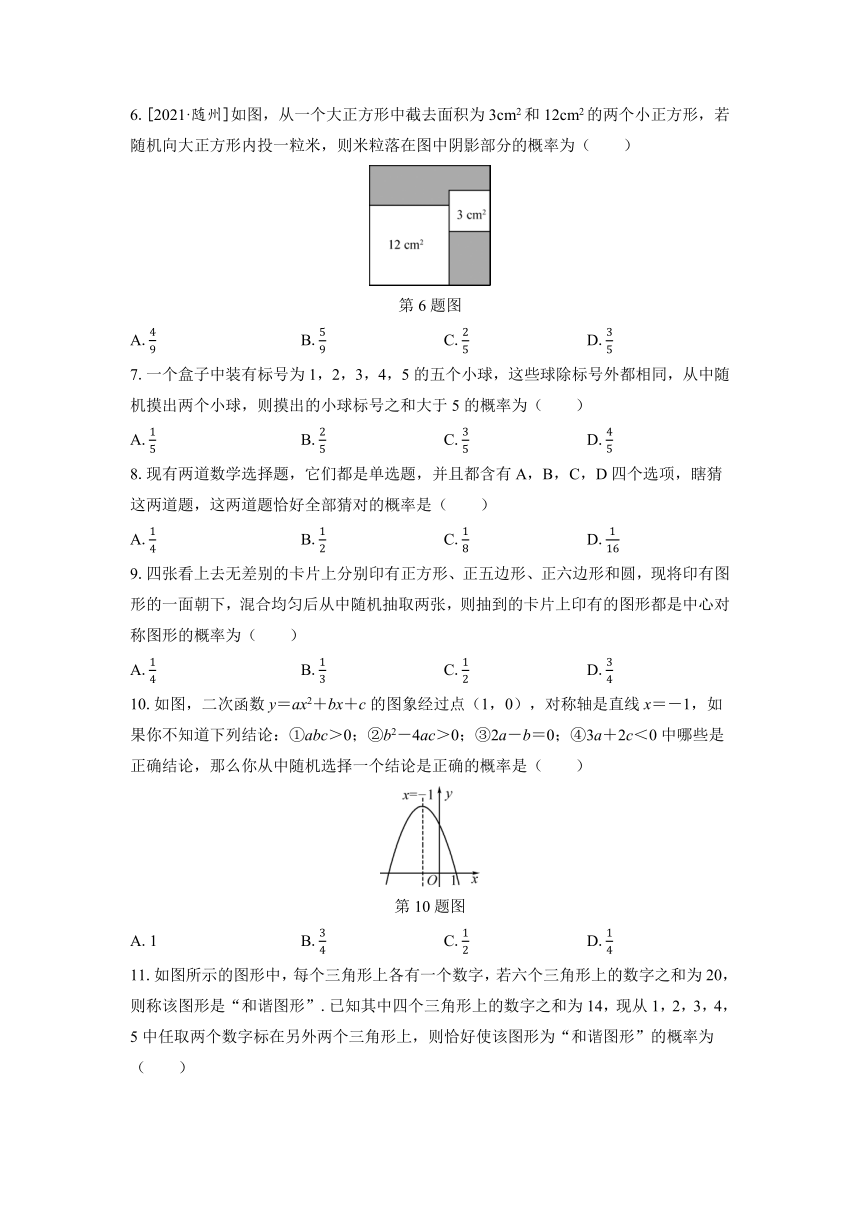
6.[2021·随州]如图,从一个大正方形中截去面积为3cm2和12cm2的两个小正方形,若随机向大正方形内投一粒米,则米粒落在图中阴影部分的概率为( )
第6题图
A. B. C. D.
7.一个盒子中装有标号为1,2,3,4,5的五个小球,这些球除标号外都相同,从中随机摸出两个小球,则摸出的小球标号之和大于5的概率为( )
A. B. C. D.
8.现有两道数学选择题,它们都是单选题,并且都含有A,B,C,D四个选项,瞎猜这两道题,这两道题恰好全部猜对的概率是( )
A. B. C. D.
9.四张看上去无差别的卡片上分别印有正方形、正五边形、正六边形和圆,现将印有图形的一面朝下,混合均匀后从中随机抽取两张,则抽到的卡片上印有的图形都是中心对称图形的概率为( )
A. B. C. D.
10.如图,二次函数y=ax2+bx+c的图象经过点(1,0),对称轴是直线x=-1,如果你不知道下列结论:①abc>0;②b2-4ac>0;③2a-b=0;④3a+2c<0中哪些是正确结论,那么你从中随机选择一个结论是正确的概率是( )
第10题图
A.1 B. C. D.
11.如图所示的图形中,每个三角形上各有一个数字,若六个三角形上的数字之和为20,则称该图形是“和谐图形”.已知其中四个三角形上的数字之和为14,现从1,2,3,4,5中任取两个数字标在另外两个三角形上,则恰好使该图形为“和谐图形”的概率为( )
第11题图
A. B. C. D.
12.[2023·海淀期末]如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟不落在花圃上的概率为( )
第12题图
A. B. C. D.
二、填空题(共6小题,每小题4分,共24分)
13.下表记录了某种幼树在一定条件下移植成活的情况:
移植总数n 400 1 500 3 500 7 000 9 000 14 000
成活数m 325 1 336 3 203 6 335 8 073 12 628
成活的频率 (精确到0.001) 0.813 0.891 0.915 0.905 0.897 0.902
由此估计这种幼树在此条件下移植成活的概率是 (精确到0.1).
14.如图所示的转盘被分成面积相等的四个扇形,分别涂有红、黄、蓝、绿四种颜色.固定指针,自由转动转盘两次,每次停止后,记下指针所指区域(指针指向区域分界线时,忽略不计)的颜色,则两次颜色相同的概率是 .
15.某校欲从九年级某班3名女生,2名男生中任选两名学生,代表学校参加全市举办的“中国梦·青春梦”演讲比赛,恰好选中一男一女的概率是 .
16.某产品出现次品的概率为0.05,任意抽取这种产品600件,那么大约有 件是次品.
17.一个不透明的盒子中装有除标号外完全相同的4个小球,小球上分别标有数字-4,-2,3,5,从盒子中随机抽取一个小球,小球上的数记为a,再从剩下的球中随机抽取一个小球,小球上的数记为b,则使得点(a,a-b)在第四象限的概率为 .
18.已知函数y=(2k-1)x+4(k为常数),若从-3≤k≤3中任取k的值,则得到的函数是具有性质“y随x的增大而增大”的一次函数的概率为 .
三、解答题(共90分)
19.(12分)[2023·清远]已知一个口袋中装有8个只有颜色不同的球,其中3个白球,5个黑球.
(1)从中随机抽取出一个黑球的概率是多少?
(2)若往口袋中再放入3个白球,求从口袋中随机抽取出一个白球的概率.
20.(12分)“草莓音乐节”组委会设置了甲、乙、丙三类门票,某班购买了甲类门票3张,乙类门票7张,丙类门票10张,班长采取在全班同学中随机抽取的方式来确定观众名单,且每个同学只有一次机会,已知该班有50名学生.请根据题意解决以下问题:
(1)该班某个学生恰能去参加“音乐节”活动的概率是多少?
(2)该班同学强烈呼吁甲类门票太少,要求每人抽到甲类门票的概率要达到20%,则还要购买甲票多少张?
21.(12分)如图1、图2是可以自由转动的两个转盘.图1被平均分成9等份,分别标有1,2,3,4,5,6,7,8,9这9个数字,转动转盘,当转盘停止后,指针指向的数字即为转出的数字.图2被涂上红色与绿色,绿色部分的扇形圆心角是120°,转动转盘,当转盘停止后,指针指向的颜色即为转出的颜色.小明转动图1的转盘,小亮转动图2的转盘.若某个转盘的指针恰好指在分界线上时重转.小颖认为:小明转出的数字小于7的概率与小亮转出的颜色是红色的概率相同.小颖的观点对吗?为什么?
图1 图2
22.(12分)同时抛掷两枚质地均匀的正四面体骰子,骰子各个面的点数分别是1至4的整数,把这两枚骰子向下的面的点数记为(a,b),其中第一枚骰子的点数记为a,第二枚骰子的点数记为b.
(1)用列举法或画树状图法求(a,b)的结果有多少种?
(2)求方程x2+bx+a=0有实数解的概率.
23.(12分)[2021·常州]在3张相同的小纸条上,分别写上条件:①四边形ABCD是菱形;②四边形ABCD有一个内角是直角;③四边形ABCD的对角线相等.将这3张小纸条做成3支签,放在一个不透明的盒子中.
(1)搅匀后从中任意抽出1支签,抽到条件①的概率是 ;
(2)搅匀后先从中任意抽出1支签(不放回),再从余下的2支签中任意抽出1支签,四边形ABCD同时满足抽到的2张小纸条上的条件,求四边形ABCD一定是正方形的概率.
24.(14分)在学习“轴对称现象”内容时,王老师让同学们寻找身边的轴对称图形.小明有一副三角尺和一个量角器(如图所示).
(1)小明在这三件文具中任取一件,结果是轴对称图形的概率是 ;
(2)小明把A,B两把尺子的各任意一个角拼在一起(无重叠无缝隙)得到一个更大的角,请用画树状图或列表的方法求这个角是钝角的概率.
25.(16分)某公司的午餐采用自助的形式,并倡导员工“适度取餐,减少浪费”.该公司共有10个部门,且各部门的人数相同.为了解午餐的浪费情况,公司从这10个部门中随机抽取了A,B两个部门,进行了连续四周(20个工作日)的调查,得到这两个部门每天午餐浪费饭菜的重量,以下简称“每日餐余重量”(单位:千克),并对这些数据进行了整理、描述和分析.下面给出了部分信息.
a. A部门每日餐余重量的频数分布直方图如下(数据分成6组:0≤x<2,2≤x<4,4≤x<6,6≤x<8,8≤x<10,10≤x≤12);
b. A部门每日餐余重量在6≤x<8这一组的是:6.1,6.6,7.0,7.0,7.0,7.8;
c. B部门每日餐余重量如下:
第1周 1.4 2.8 6.9 7.8 1.9
第2周 6.9 2.6 7.5 6.9 9.5
第3周 9.7 3.1 4.6 6.9 10.8
第4周 7.8 8.4 8.3 9.4 8.8
d. A,B两个部门这20个工作日每日餐余重量的平均数、中位数、众数如下:
部门 平均数 中位数 众数
A 6.4 m 7.0
B 6.6 7.2 n
根据以上信息,回答下列问题:
(1)写出表中m,n的值,m= ,n= ;
(2)在A,B这两个部门中,“适度取餐,减少浪费”做得较好的部门是 (填“A”或“B”),理由是 ;
(3)结合A,B这两个部门每日餐余重量的数据,估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量;
(4)食堂工作人员从B部门第1周和第2周各抽查一日餐余重量,两日餐余重量刚好都是n的概率是多少?
参考答案
1. B 2. A 3. A 4. C 5. D 6. A 7. C
8. D 9. C 10. B 11. B 12. A 13.0.9
14. 15. 16.30 17. 18.
19.(1)从中随机抽取出一个黑球的概率是.
(2)从口袋中随机抽取出一个白球的概率是.
20.(1)该班某个学生恰能去参加“音乐节”活动的概率为.
(2)还要购买甲类门票7张.
21.小颖的观点是对的.理由略.
22.(1)(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),一共有16种结果.
(2)此方程有解的概率是.
23.(1)
(2)四边形ABCD一定是正方形的概率是.
24.(1) (2)这个角是钝角的概率是.
25.(1)6.8 6.9 (2)A A部门的平均数和中位数相对较小,浪费的少
(3)估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量为15600千克.
(4)两日餐余重量刚好都是6.9的概率为.
[时间:90分钟 分值:150分]
一、选择题(共12小题,每小题3分,共36分)
1.下列所给的事件中,是必然事件的是( )
A.买10注福利彩票会中奖
B.某校的400名学生中,至少有2名学生的生日是同一天
C.连续4次投掷质地均匀的硬币,会有1次硬币正面朝上
D.2024年的春节假期成都会下雪
2.成语是中华文化的瑰宝,是中华文化的微缩景观.下列成语:①水中捞月;②守株待兔;③百步穿杨;④瓮中捉鳖.描述的事件是不可能事件的是( )
A.① B.② C.③ D.④
3.[2022·临海]某路口红绿灯的时间设置如下:绿灯60秒,红灯40秒,黄灯3秒.当车随机经过该路口,遇到哪一种灯的可能性最大( )
A.绿灯 B.红灯 C.黄灯 D.不能确定
4.一个纸箱中装有白色和黄色两种乒乓球,共20个,这些球除颜色外都相同,将球搅匀,每次从中随机摸出一个球,记下颜色后放回、搅匀再摸球,通过大量重复摸球试验后,将摸到白球的频率绘制成如图所示的统计图,由此可估计纸箱中白球的个数为( )
第4题图
A.4 B.6 C.8 D.10
5.[2023·瑞安]如图,某展览大厅有A,B两个入口,C,D,E三个出口,小明任选一个入口进入展览大厅,参观结束后任选一个出口离开,不同的出入路线一共有( )
第5题图
A.3种 B.4种 C.5种 D.6种
6.[2021·随州]如图,从一个大正方形中截去面积为3cm2和12cm2的两个小正方形,若随机向大正方形内投一粒米,则米粒落在图中阴影部分的概率为( )
第6题图
A. B. C. D.
7.一个盒子中装有标号为1,2,3,4,5的五个小球,这些球除标号外都相同,从中随机摸出两个小球,则摸出的小球标号之和大于5的概率为( )
A. B. C. D.
8.现有两道数学选择题,它们都是单选题,并且都含有A,B,C,D四个选项,瞎猜这两道题,这两道题恰好全部猜对的概率是( )
A. B. C. D.
9.四张看上去无差别的卡片上分别印有正方形、正五边形、正六边形和圆,现将印有图形的一面朝下,混合均匀后从中随机抽取两张,则抽到的卡片上印有的图形都是中心对称图形的概率为( )
A. B. C. D.
10.如图,二次函数y=ax2+bx+c的图象经过点(1,0),对称轴是直线x=-1,如果你不知道下列结论:①abc>0;②b2-4ac>0;③2a-b=0;④3a+2c<0中哪些是正确结论,那么你从中随机选择一个结论是正确的概率是( )
第10题图
A.1 B. C. D.
11.如图所示的图形中,每个三角形上各有一个数字,若六个三角形上的数字之和为20,则称该图形是“和谐图形”.已知其中四个三角形上的数字之和为14,现从1,2,3,4,5中任取两个数字标在另外两个三角形上,则恰好使该图形为“和谐图形”的概率为( )
第11题图
A. B. C. D.
12.[2023·海淀期末]如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟不落在花圃上的概率为( )
第12题图
A. B. C. D.
二、填空题(共6小题,每小题4分,共24分)
13.下表记录了某种幼树在一定条件下移植成活的情况:
移植总数n 400 1 500 3 500 7 000 9 000 14 000
成活数m 325 1 336 3 203 6 335 8 073 12 628
成活的频率 (精确到0.001) 0.813 0.891 0.915 0.905 0.897 0.902
由此估计这种幼树在此条件下移植成活的概率是 (精确到0.1).
14.如图所示的转盘被分成面积相等的四个扇形,分别涂有红、黄、蓝、绿四种颜色.固定指针,自由转动转盘两次,每次停止后,记下指针所指区域(指针指向区域分界线时,忽略不计)的颜色,则两次颜色相同的概率是 .
15.某校欲从九年级某班3名女生,2名男生中任选两名学生,代表学校参加全市举办的“中国梦·青春梦”演讲比赛,恰好选中一男一女的概率是 .
16.某产品出现次品的概率为0.05,任意抽取这种产品600件,那么大约有 件是次品.
17.一个不透明的盒子中装有除标号外完全相同的4个小球,小球上分别标有数字-4,-2,3,5,从盒子中随机抽取一个小球,小球上的数记为a,再从剩下的球中随机抽取一个小球,小球上的数记为b,则使得点(a,a-b)在第四象限的概率为 .
18.已知函数y=(2k-1)x+4(k为常数),若从-3≤k≤3中任取k的值,则得到的函数是具有性质“y随x的增大而增大”的一次函数的概率为 .
三、解答题(共90分)
19.(12分)[2023·清远]已知一个口袋中装有8个只有颜色不同的球,其中3个白球,5个黑球.
(1)从中随机抽取出一个黑球的概率是多少?
(2)若往口袋中再放入3个白球,求从口袋中随机抽取出一个白球的概率.
20.(12分)“草莓音乐节”组委会设置了甲、乙、丙三类门票,某班购买了甲类门票3张,乙类门票7张,丙类门票10张,班长采取在全班同学中随机抽取的方式来确定观众名单,且每个同学只有一次机会,已知该班有50名学生.请根据题意解决以下问题:
(1)该班某个学生恰能去参加“音乐节”活动的概率是多少?
(2)该班同学强烈呼吁甲类门票太少,要求每人抽到甲类门票的概率要达到20%,则还要购买甲票多少张?
21.(12分)如图1、图2是可以自由转动的两个转盘.图1被平均分成9等份,分别标有1,2,3,4,5,6,7,8,9这9个数字,转动转盘,当转盘停止后,指针指向的数字即为转出的数字.图2被涂上红色与绿色,绿色部分的扇形圆心角是120°,转动转盘,当转盘停止后,指针指向的颜色即为转出的颜色.小明转动图1的转盘,小亮转动图2的转盘.若某个转盘的指针恰好指在分界线上时重转.小颖认为:小明转出的数字小于7的概率与小亮转出的颜色是红色的概率相同.小颖的观点对吗?为什么?
图1 图2
22.(12分)同时抛掷两枚质地均匀的正四面体骰子,骰子各个面的点数分别是1至4的整数,把这两枚骰子向下的面的点数记为(a,b),其中第一枚骰子的点数记为a,第二枚骰子的点数记为b.
(1)用列举法或画树状图法求(a,b)的结果有多少种?
(2)求方程x2+bx+a=0有实数解的概率.
23.(12分)[2021·常州]在3张相同的小纸条上,分别写上条件:①四边形ABCD是菱形;②四边形ABCD有一个内角是直角;③四边形ABCD的对角线相等.将这3张小纸条做成3支签,放在一个不透明的盒子中.
(1)搅匀后从中任意抽出1支签,抽到条件①的概率是 ;
(2)搅匀后先从中任意抽出1支签(不放回),再从余下的2支签中任意抽出1支签,四边形ABCD同时满足抽到的2张小纸条上的条件,求四边形ABCD一定是正方形的概率.
24.(14分)在学习“轴对称现象”内容时,王老师让同学们寻找身边的轴对称图形.小明有一副三角尺和一个量角器(如图所示).
(1)小明在这三件文具中任取一件,结果是轴对称图形的概率是 ;
(2)小明把A,B两把尺子的各任意一个角拼在一起(无重叠无缝隙)得到一个更大的角,请用画树状图或列表的方法求这个角是钝角的概率.
25.(16分)某公司的午餐采用自助的形式,并倡导员工“适度取餐,减少浪费”.该公司共有10个部门,且各部门的人数相同.为了解午餐的浪费情况,公司从这10个部门中随机抽取了A,B两个部门,进行了连续四周(20个工作日)的调查,得到这两个部门每天午餐浪费饭菜的重量,以下简称“每日餐余重量”(单位:千克),并对这些数据进行了整理、描述和分析.下面给出了部分信息.
a. A部门每日餐余重量的频数分布直方图如下(数据分成6组:0≤x<2,2≤x<4,4≤x<6,6≤x<8,8≤x<10,10≤x≤12);
b. A部门每日餐余重量在6≤x<8这一组的是:6.1,6.6,7.0,7.0,7.0,7.8;
c. B部门每日餐余重量如下:
第1周 1.4 2.8 6.9 7.8 1.9
第2周 6.9 2.6 7.5 6.9 9.5
第3周 9.7 3.1 4.6 6.9 10.8
第4周 7.8 8.4 8.3 9.4 8.8
d. A,B两个部门这20个工作日每日餐余重量的平均数、中位数、众数如下:
部门 平均数 中位数 众数
A 6.4 m 7.0
B 6.6 7.2 n
根据以上信息,回答下列问题:
(1)写出表中m,n的值,m= ,n= ;
(2)在A,B这两个部门中,“适度取餐,减少浪费”做得较好的部门是 (填“A”或“B”),理由是 ;
(3)结合A,B这两个部门每日餐余重量的数据,估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量;
(4)食堂工作人员从B部门第1周和第2周各抽查一日餐余重量,两日餐余重量刚好都是n的概率是多少?
参考答案
1. B 2. A 3. A 4. C 5. D 6. A 7. C
8. D 9. C 10. B 11. B 12. A 13.0.9
14. 15. 16.30 17. 18.
19.(1)从中随机抽取出一个黑球的概率是.
(2)从口袋中随机抽取出一个白球的概率是.
20.(1)该班某个学生恰能去参加“音乐节”活动的概率为.
(2)还要购买甲类门票7张.
21.小颖的观点是对的.理由略.
22.(1)(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),一共有16种结果.
(2)此方程有解的概率是.
23.(1)
(2)四边形ABCD一定是正方形的概率是.
24.(1) (2)这个角是钝角的概率是.
25.(1)6.8 6.9 (2)A A部门的平均数和中位数相对较小,浪费的少
(3)估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量为15600千克.
(4)两日餐余重量刚好都是6.9的概率为.
同课章节目录
