2016年北师大版九年级数学下册第三章圆检测题含答案
文档属性
| 名称 | 2016年北师大版九年级数学下册第三章圆检测题含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 450.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-31 00:00:00 | ||
图片预览

文档简介
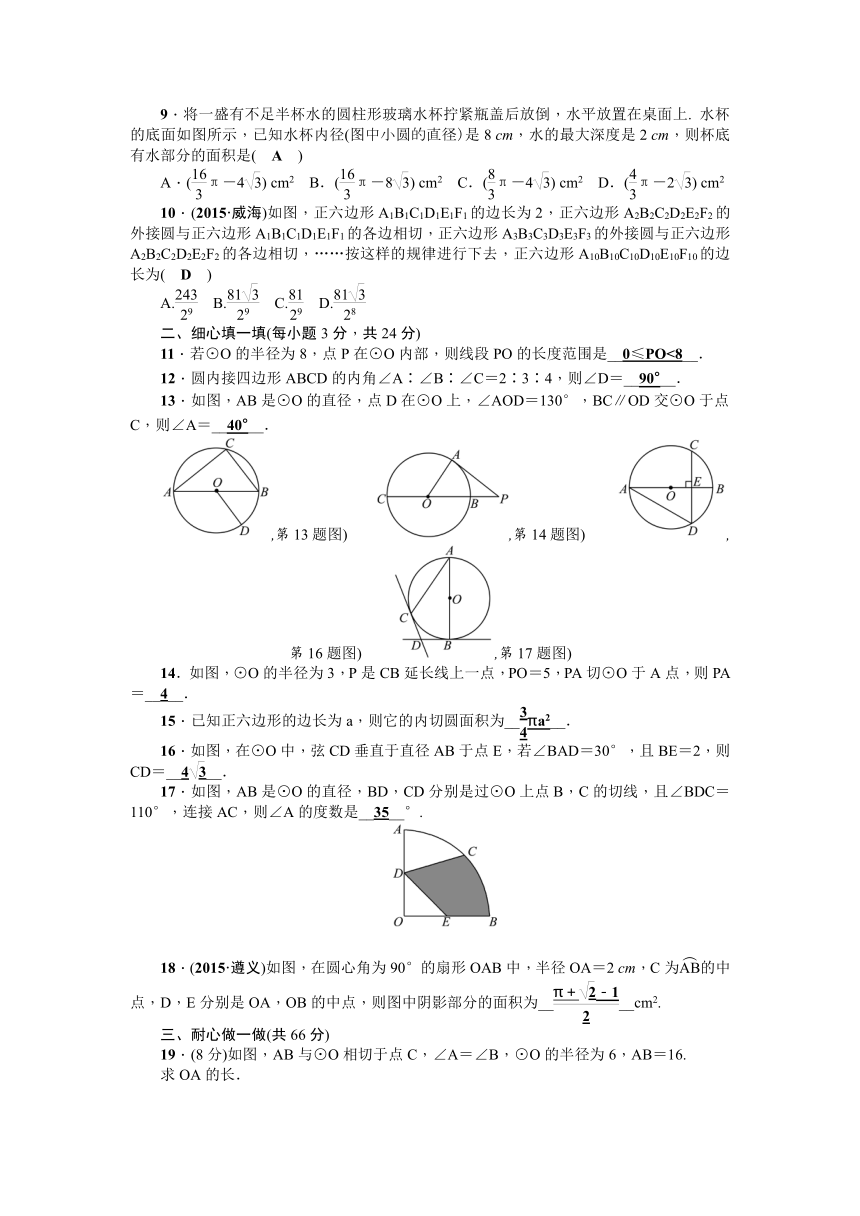
第三章检测题
时间:120分钟 满分:120分
一、精心选一选(每小题3分,共30分)
1.下列判断中正确的是( C )
A.平分弦的直径垂直于弦 B.平分弦的直线也必平分弦所对的两条弧
C.弦的垂直平分线必平分弦所对的两条弧 D.平分一条弧的直线必平分这条弧所对的弦
2.在⊙O中,同一条弦AB所对的圆周角( D )
A.相等 B.互补 C.互余 D.相等或互补
3.如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于( B )
A.116° B.32° C.58° D.64°
,第3题图) ,第4题图) ,第5题图) ,第6题图)
4.如图,石拱桥的桥顶到水面的距离CD为8 m,桥拱半径OC为5 m,则水面宽AB为( D )
A.4 m B.5 m C.6 m D.8 m
5.如图,AB是⊙O的直径,C,D是⊙O上的点,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( A )
A.40° B.50° C.60° D.70°
6.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PB切⊙O于点B,则PB的最小值是( C )
A. B.3 C. D.2
7.如图是一把扇子,其中∠AOB为120°,OC长为8 cm,CA长为12 cm,则阴影部分的面积为( C )
A.152π cm2 B.144π cm2 C.112π cm2 D.64π cm2
,第7题图) ,第8题图) ,第9题图) ,第10题图)
8.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( B )
A.第①块 B.第②块 C.第③块 D.第④块
9.将一盛有不足半杯水的圆柱形玻璃水杯拧紧瓶盖后放倒,水平放置在桌面上. 水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8 cm,水的最大深度是2 cm,则杯底有水部分的面积是( A )
A.(π-4) cm2 B.(π-8) cm2 C.(π-4) cm2 D.(π-2) cm2
10.(2015·威海)如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,……按这样的规律进行下去,正六边形A10B10C10D10E10F10的边长为( D )
A. B. C. D.
二、细心填一填(每小题3分,共24分)
11.若⊙O的半径为8,点P在⊙O内部,则线段PO的长度范围是__0≤PO<8__.
12.圆内接四边形ABCD的内角∠A∶∠B∶∠C=2∶3∶4,则∠D=__90°__.
13.如图,AB是⊙O的直径,点D在⊙O上,∠AOD=130°,BC∥OD交⊙O于点C,则∠A=__40°__.
,第13题图) ,第14题图) ,第16题图) ,第17题图)
14.如图,⊙O的半径为3,P是CB延长线上一点,PO=5,PA切⊙O于A点,则PA=__4__.
15.已知正六边形的边长为a,则它的内切圆面积为__πa2__.
16.如图,在⊙O中,弦CD垂直于直径AB于点E,若∠BAD=30°,且BE=2,则CD=__4__.
17.如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°,连接AC,则∠A的度数是__35__°.
18.(2015·遵义)如图,在圆心角为90°的扇形OAB中,半径OA=2 cm,C为的中点,D,E分别是OA,OB的中点,则图中阴影部分的面积为____cm2.
三、耐心做一做(共66分)
19.(8分)如图,AB与⊙O相切于点C,∠A=∠B,⊙O的半径为6,AB=16.
求OA的长.
解:连接OC.∵AB与⊙O相切于点C,∴OC⊥AB,∵∠A=∠B,∴OA=OB,∴AC=BC=AB=8,∵OC=6,∴OA==10
20.(8分)如图,两个同心圆中,大圆的弦AB,AC分别切小圆于点D,E,△ABC的周长为12 cm,求△ADE的周长.
解:连接OD,OE.∵AB,AC分别切小⊙O于点D,E,∴OD⊥AB,OE⊥AC,∴AD=DB,AE=EC,∴DE是△ABC的中位线,∴DE=BC,∴C△ADE=C△ABC=×12=6(cm)
21.(9分)如图,⊙O的直径AB长为6,弦AC长为2,∠ACB的平分线交⊙O于点D,求四边形ADBC的面积.
解:∵AB是⊙O的直径,∴∠ACB=∠ADB=90°.在Rt△ABC中,由勾股定理,得BC==4.∵CD平分∠ACB,∴=,∴AD=BD.在Rt△ABD中,由勾股定理,得AD=DB=AB=×6=3,∴S四边形ADBC=S△ABC+S△ABD=AC·BC+AD·BD=×2×4+×3×3=4+3
22.(9分)如图,AB是⊙O的弦,OA⊥OD,AB,OD交于点C,且CD=BD.
(1)判断BD与⊙O的位置关系,并证明你的结论;
(2)当OA=3,OC=1时,求线段BD的长.
解:(1)BD与⊙O相切.证明:连接OB.∵OA=OB,∴∠OAC=∠OBC.∵OA⊥OD,∴∠AOC=90°,∴∠OAC+∠OCA=90°.∵DC=DB,∴∠DCB=∠DBC.∵∠DCB=∠ACO,∴∠ACO=∠DBC,∴∠DBC+∠OBC=90°,∴∠OBD=90°,即OB⊥BD,∴BD与⊙O相切
(2)设BD=x,则CD=x,OD=x+1 ,OB=OA=3,由勾股定理得32+x2=(x+1)2,解得x=4,∴BD=4
23.(10分)(2015·安徽)在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
(1)如图1,当PQ∥AB时,求PQ长;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
解:(1)∵OP⊥PQ,PQ∥AB,∴OP⊥AB.在Rt△OPB中,OP=OB·tan∠ABC=3·tan30°=.连接OQ,在Rt△OPQ中,PQ=== (2)∵PQ2=OQ2-OP2=9-OP2,∴当OP最小时,PQ最大,此时OP⊥BC,OP=OB·sin∠ABC=3·sin30°=,∴PQ长的最大值为=
24.(10分)如图,在⊙O中,AB是直径,点D是⊙O上一点,且∠BOD=60°,过点D作⊙O的切线CD交AB延长线于点C,E为AD的中点,连接DE,EB.
(1)求证:四边形BCDE是平行四边形;
(2)已知图中阴影部分面积为6π,求⊙O的半径r.
解:(1)连接OE,∵∠BOD=60°,∴∠AOD=120°,∴=,∵E为的中点,∴==,∴∠EOD=∠BOD=60°,OD⊥BE,∵OE=OD,∴△ODE是等边三角形,∴∠ODE=60°,∴∠ODE=∠BOD,∴DE∥BC,又DC是⊙O的切线,∴OD⊥DC,∴BE∥DC,∴四边形BCDE是平行四边形 (2)由(1)知DE=OD=OB,∠ODE=∠BOD=60°,设OD与BE交于F,则∠DFE=∠OFB,∴△EDF≌△BOF,∴S△EDF=S△BOF,∴S阴影=S扇形OBD,∴πr2=6π,∴r=6
25.(12分)(2015·呼和浩特)如图,⊙O是△ABC的外接圆,P是⊙O外的一点,AM是⊙O的直径,∠PAC=∠ABC.
(1)求证:PA是⊙O的切线;
(2)连接PB与AC交于点D,与⊙O交于点E,F为BD上的一点,若M为的中点,且∠DCF=∠P,求证:==.
解:(1)连接CM.∵∠PAC=∠ABC,∠M=∠ABC,∴∠PAC=∠M.∵AM为直径,∴∠M+∠MAC=90°,∴∠PAC+∠MAC=90°,即∠MAP=90°,∴MA⊥AP,∴PA是⊙O的切线 (2)连接AE.∵M为中点,AM为⊙O的直径,∴AM⊥BC.∵AM⊥AP,∴AP∥BC,∴△ADP∽△CDB,∴=.∵AP∥BC,∴∠P=∠CBD.∵∠CBD=∠CAE,∴∠P=∠CAE.∵∠P=∠DCF,∴∠DCF=∠CAE.又∵∠ADE=∠CDF,∴△ADE∽△CDF,∴=,∴==
时间:120分钟 满分:120分
一、精心选一选(每小题3分,共30分)
1.下列判断中正确的是( C )
A.平分弦的直径垂直于弦 B.平分弦的直线也必平分弦所对的两条弧
C.弦的垂直平分线必平分弦所对的两条弧 D.平分一条弧的直线必平分这条弧所对的弦
2.在⊙O中,同一条弦AB所对的圆周角( D )
A.相等 B.互补 C.互余 D.相等或互补
3.如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于( B )
A.116° B.32° C.58° D.64°
,第3题图) ,第4题图) ,第5题图) ,第6题图)
4.如图,石拱桥的桥顶到水面的距离CD为8 m,桥拱半径OC为5 m,则水面宽AB为( D )
A.4 m B.5 m C.6 m D.8 m
5.如图,AB是⊙O的直径,C,D是⊙O上的点,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( A )
A.40° B.50° C.60° D.70°
6.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PB切⊙O于点B,则PB的最小值是( C )
A. B.3 C. D.2
7.如图是一把扇子,其中∠AOB为120°,OC长为8 cm,CA长为12 cm,则阴影部分的面积为( C )
A.152π cm2 B.144π cm2 C.112π cm2 D.64π cm2
,第7题图) ,第8题图) ,第9题图) ,第10题图)
8.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( B )
A.第①块 B.第②块 C.第③块 D.第④块
9.将一盛有不足半杯水的圆柱形玻璃水杯拧紧瓶盖后放倒,水平放置在桌面上. 水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8 cm,水的最大深度是2 cm,则杯底有水部分的面积是( A )
A.(π-4) cm2 B.(π-8) cm2 C.(π-4) cm2 D.(π-2) cm2
10.(2015·威海)如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,……按这样的规律进行下去,正六边形A10B10C10D10E10F10的边长为( D )
A. B. C. D.
二、细心填一填(每小题3分,共24分)
11.若⊙O的半径为8,点P在⊙O内部,则线段PO的长度范围是__0≤PO<8__.
12.圆内接四边形ABCD的内角∠A∶∠B∶∠C=2∶3∶4,则∠D=__90°__.
13.如图,AB是⊙O的直径,点D在⊙O上,∠AOD=130°,BC∥OD交⊙O于点C,则∠A=__40°__.
,第13题图) ,第14题图) ,第16题图) ,第17题图)
14.如图,⊙O的半径为3,P是CB延长线上一点,PO=5,PA切⊙O于A点,则PA=__4__.
15.已知正六边形的边长为a,则它的内切圆面积为__πa2__.
16.如图,在⊙O中,弦CD垂直于直径AB于点E,若∠BAD=30°,且BE=2,则CD=__4__.
17.如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°,连接AC,则∠A的度数是__35__°.
18.(2015·遵义)如图,在圆心角为90°的扇形OAB中,半径OA=2 cm,C为的中点,D,E分别是OA,OB的中点,则图中阴影部分的面积为____cm2.
三、耐心做一做(共66分)
19.(8分)如图,AB与⊙O相切于点C,∠A=∠B,⊙O的半径为6,AB=16.
求OA的长.
解:连接OC.∵AB与⊙O相切于点C,∴OC⊥AB,∵∠A=∠B,∴OA=OB,∴AC=BC=AB=8,∵OC=6,∴OA==10
20.(8分)如图,两个同心圆中,大圆的弦AB,AC分别切小圆于点D,E,△ABC的周长为12 cm,求△ADE的周长.
解:连接OD,OE.∵AB,AC分别切小⊙O于点D,E,∴OD⊥AB,OE⊥AC,∴AD=DB,AE=EC,∴DE是△ABC的中位线,∴DE=BC,∴C△ADE=C△ABC=×12=6(cm)
21.(9分)如图,⊙O的直径AB长为6,弦AC长为2,∠ACB的平分线交⊙O于点D,求四边形ADBC的面积.
解:∵AB是⊙O的直径,∴∠ACB=∠ADB=90°.在Rt△ABC中,由勾股定理,得BC==4.∵CD平分∠ACB,∴=,∴AD=BD.在Rt△ABD中,由勾股定理,得AD=DB=AB=×6=3,∴S四边形ADBC=S△ABC+S△ABD=AC·BC+AD·BD=×2×4+×3×3=4+3
22.(9分)如图,AB是⊙O的弦,OA⊥OD,AB,OD交于点C,且CD=BD.
(1)判断BD与⊙O的位置关系,并证明你的结论;
(2)当OA=3,OC=1时,求线段BD的长.
解:(1)BD与⊙O相切.证明:连接OB.∵OA=OB,∴∠OAC=∠OBC.∵OA⊥OD,∴∠AOC=90°,∴∠OAC+∠OCA=90°.∵DC=DB,∴∠DCB=∠DBC.∵∠DCB=∠ACO,∴∠ACO=∠DBC,∴∠DBC+∠OBC=90°,∴∠OBD=90°,即OB⊥BD,∴BD与⊙O相切
(2)设BD=x,则CD=x,OD=x+1 ,OB=OA=3,由勾股定理得32+x2=(x+1)2,解得x=4,∴BD=4
23.(10分)(2015·安徽)在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
(1)如图1,当PQ∥AB时,求PQ长;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
解:(1)∵OP⊥PQ,PQ∥AB,∴OP⊥AB.在Rt△OPB中,OP=OB·tan∠ABC=3·tan30°=.连接OQ,在Rt△OPQ中,PQ=== (2)∵PQ2=OQ2-OP2=9-OP2,∴当OP最小时,PQ最大,此时OP⊥BC,OP=OB·sin∠ABC=3·sin30°=,∴PQ长的最大值为=
24.(10分)如图,在⊙O中,AB是直径,点D是⊙O上一点,且∠BOD=60°,过点D作⊙O的切线CD交AB延长线于点C,E为AD的中点,连接DE,EB.
(1)求证:四边形BCDE是平行四边形;
(2)已知图中阴影部分面积为6π,求⊙O的半径r.
解:(1)连接OE,∵∠BOD=60°,∴∠AOD=120°,∴=,∵E为的中点,∴==,∴∠EOD=∠BOD=60°,OD⊥BE,∵OE=OD,∴△ODE是等边三角形,∴∠ODE=60°,∴∠ODE=∠BOD,∴DE∥BC,又DC是⊙O的切线,∴OD⊥DC,∴BE∥DC,∴四边形BCDE是平行四边形 (2)由(1)知DE=OD=OB,∠ODE=∠BOD=60°,设OD与BE交于F,则∠DFE=∠OFB,∴△EDF≌△BOF,∴S△EDF=S△BOF,∴S阴影=S扇形OBD,∴πr2=6π,∴r=6
25.(12分)(2015·呼和浩特)如图,⊙O是△ABC的外接圆,P是⊙O外的一点,AM是⊙O的直径,∠PAC=∠ABC.
(1)求证:PA是⊙O的切线;
(2)连接PB与AC交于点D,与⊙O交于点E,F为BD上的一点,若M为的中点,且∠DCF=∠P,求证:==.
解:(1)连接CM.∵∠PAC=∠ABC,∠M=∠ABC,∴∠PAC=∠M.∵AM为直径,∴∠M+∠MAC=90°,∴∠PAC+∠MAC=90°,即∠MAP=90°,∴MA⊥AP,∴PA是⊙O的切线 (2)连接AE.∵M为中点,AM为⊙O的直径,∴AM⊥BC.∵AM⊥AP,∴AP∥BC,∴△ADP∽△CDB,∴=.∵AP∥BC,∴∠P=∠CBD.∵∠CBD=∠CAE,∴∠P=∠CAE.∵∠P=∠DCF,∴∠DCF=∠CAE.又∵∠ADE=∠CDF,∴△ADE∽△CDF,∴=,∴==
