三角函数模型的简单应用第一课
图片预览




文档简介
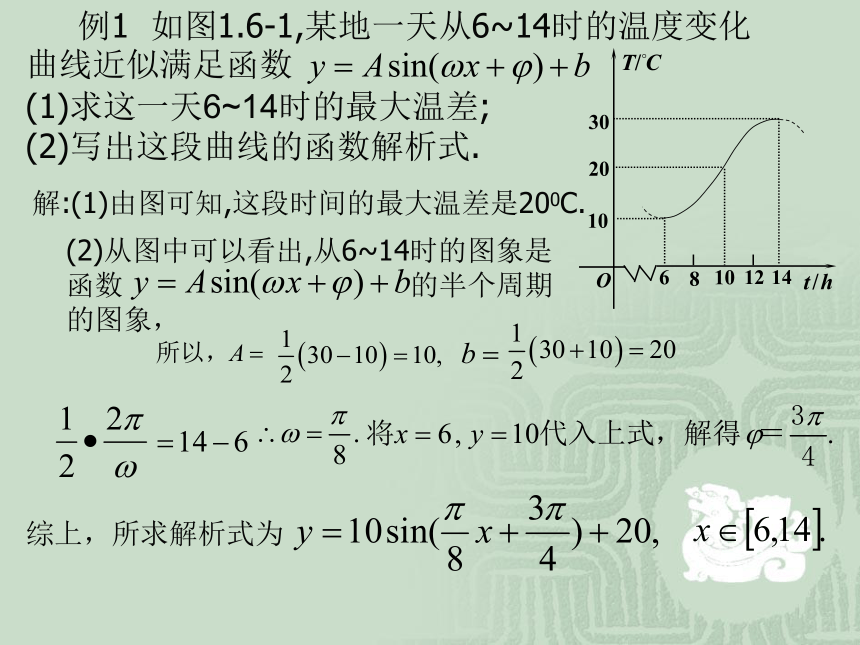
课件15张PPT。三角函数模型的简单应用解:(1)由图可知,这段时间的最大温差是200C. 例1 如图1.6-1,某地一天从6~14时的温度变化曲线近似满足函数
(1)求这一天6~14时的最大温差;
(2)写出这段曲线的函数解析式.(2)从图中可以看出,从6~14时的图象是函数 的半个周期的图象, 综上,所求解析式为【问题的思辩】:① ②得到 后,代入点 结果会怎样?代入点 结果又会怎样?【问题的反思】:
如何根据 图像求解析式中的待定参数小结求得利用最低点或最高点在图像上,该点的坐标满足函数解析式可得注意:一般地,所求出的函数模型只能近似刻画这天某个时刻的温度变化情况,因此应当特别注意自变量的变化范围.
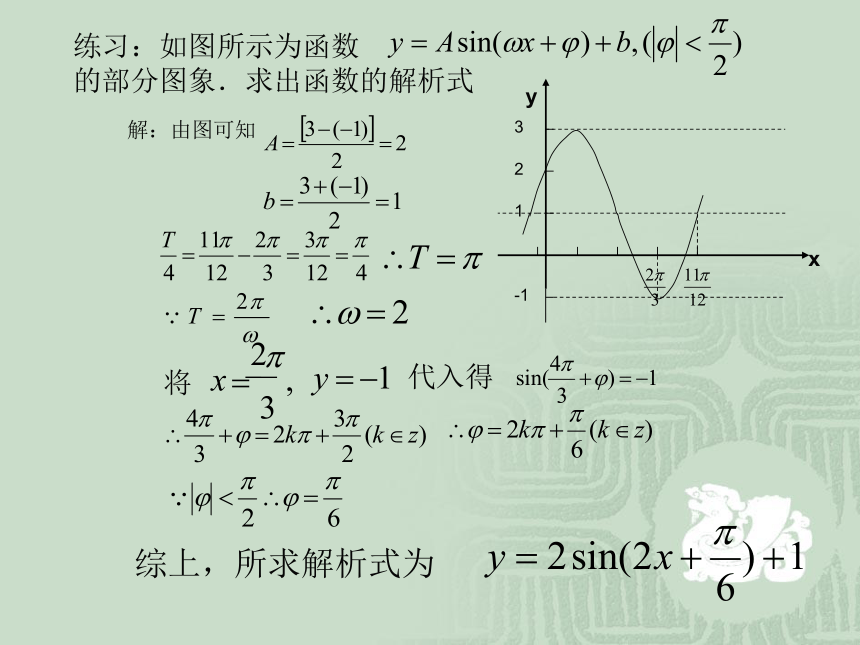
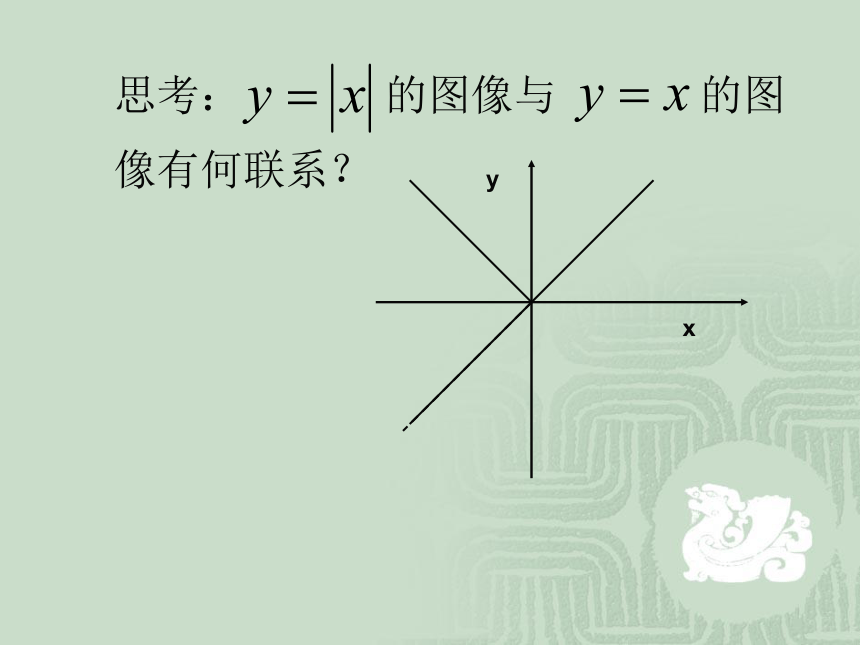
练习:如图所示为函数 的部分图象.求出函数的解析式 yx综上,所求解析式为yx思考:的图像与的图像有何联系?yx0-11【问题的思辩】:从解析式的角度如何对你的观察加以解释? 【问题的反思与深化】:根据图像写出的单调增减区间。 的单调增减区间 为注意:
利用函数图像的直观性,通过观察图像而获得对函数性质的认识,这是研究数学问题的常用方法。小结画整个函数带有绝对值的图像时:
1.先画出不含绝对值函数的图像;
2.若x轴下方有图像时,则把下面的图像以x轴为轴翻折上去。X轴上面的图像不动。总 结(1)已知函数y=Asin(ωx+φ) +b的图象,如何求其解析式?
(2)如何作出整个函数含有绝对值的图象?
(3)三角应用题的一般步骤是:搜集数据 由数据图形 利用函数模型
画出示意图 得出函数模型 解决实际问题→→作 业 设 计教科书P65页习题1.6A组2、3题谢谢大家再见
(1)求这一天6~14时的最大温差;
(2)写出这段曲线的函数解析式.(2)从图中可以看出,从6~14时的图象是函数 的半个周期的图象, 综上,所求解析式为【问题的思辩】:① ②得到 后,代入点 结果会怎样?代入点 结果又会怎样?【问题的反思】:
如何根据 图像求解析式中的待定参数小结求得利用最低点或最高点在图像上,该点的坐标满足函数解析式可得注意:一般地,所求出的函数模型只能近似刻画这天某个时刻的温度变化情况,因此应当特别注意自变量的变化范围.
练习:如图所示为函数 的部分图象.求出函数的解析式 yx综上,所求解析式为yx思考:的图像与的图像有何联系?yx0-11【问题的思辩】:从解析式的角度如何对你的观察加以解释? 【问题的反思与深化】:根据图像写出的单调增减区间。 的单调增减区间 为注意:
利用函数图像的直观性,通过观察图像而获得对函数性质的认识,这是研究数学问题的常用方法。小结画整个函数带有绝对值的图像时:
1.先画出不含绝对值函数的图像;
2.若x轴下方有图像时,则把下面的图像以x轴为轴翻折上去。X轴上面的图像不动。总 结(1)已知函数y=Asin(ωx+φ) +b的图象,如何求其解析式?
(2)如何作出整个函数含有绝对值的图象?
(3)三角应用题的一般步骤是:搜集数据 由数据图形 利用函数模型
画出示意图 得出函数模型 解决实际问题→→作 业 设 计教科书P65页习题1.6A组2、3题谢谢大家再见
