向量的加法运算及其几何意义
图片预览




文档简介
课件15张PPT。2.2.1 向量加法运算及其几何意义2.2 平面向量的线性运算教学目标:
(1)掌握向量的加法运算,并理解其几何意义;
(2)会用向量加法的三角形法则和平行四边形法则作两个向量的和向量,培养数形结合解决问题的能力;
(3)通过将向量运算与熟悉的数的运算进行类比,使学生掌握向量加法运算的交换律和结合律,并会用它们进行向量计算,渗透类比的数学方法;
教学重点:
会用向量加法的三角形法则和平行四边形法则作两个向量的和向量.
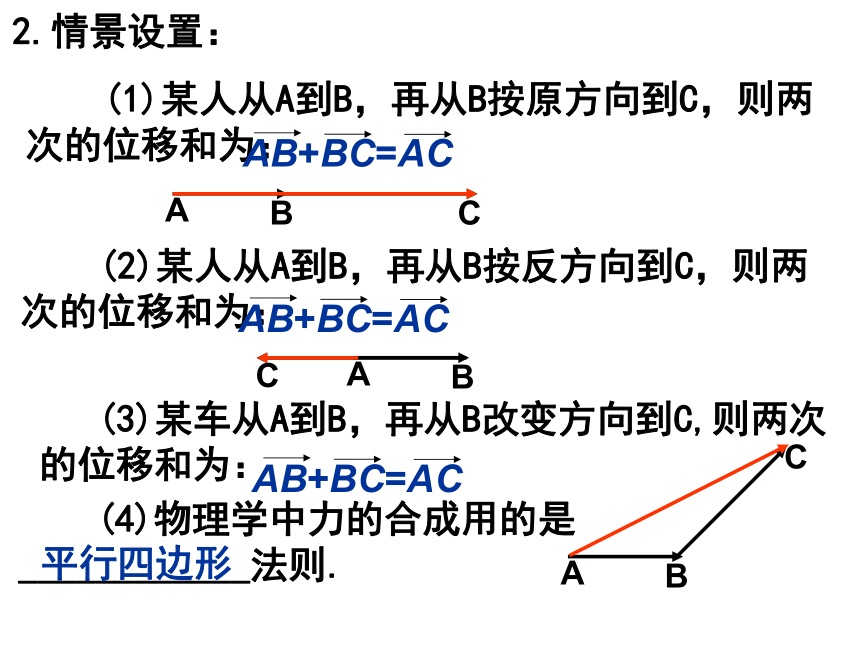
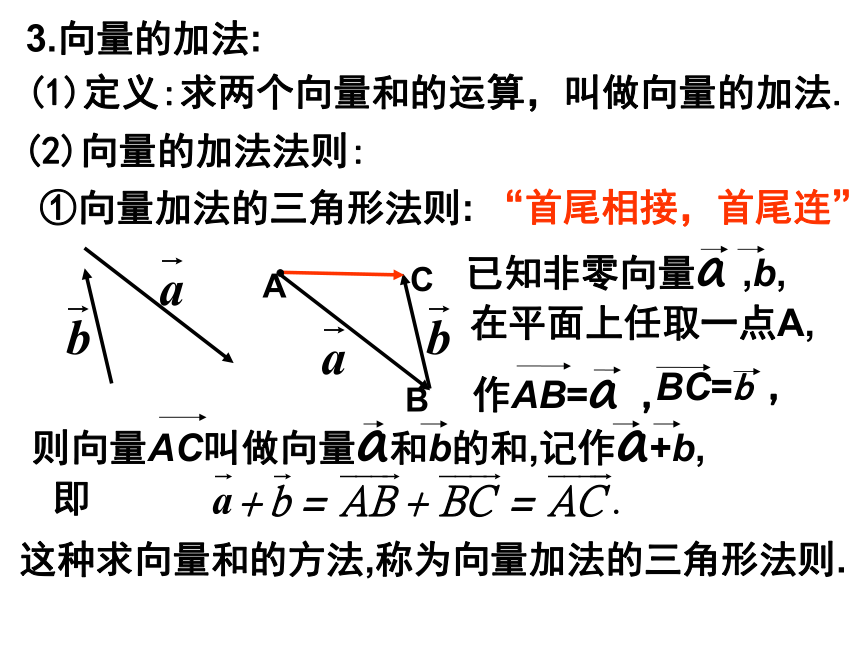
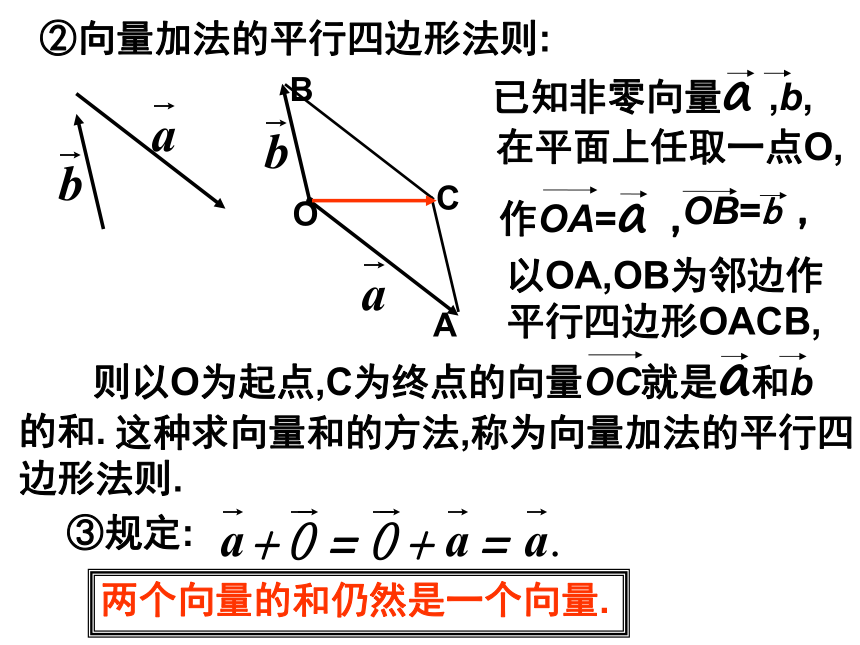
教学难点:理解向量加法的定义.〖教学情境设计〗1.复习:向量的定义以及有关概念.相等向量;平行向量;共线向量;零向量 练习:判断下列命题是否正确(1)两向量相等,则它们的起点相同,终点也相同;(2)若 ,则 或(3)若 ,则A,B,C,D四点是平行四边形的四个顶点 。(4)平行四边形ABCD中一定有(5) 若 ,则(6)若 ∥ , ∥ ,则 ∥2.情景设置: (1)某人从A到B,再从B按原方向到C,则两次的位移和为: (2)某人从A到B,再从B按反方向到C,则两次的位移和为: (3)某车从A到B,再从B改变方向到C,则两次的位移和为: (4)物理学中力的合成用的是____________法则.平行四边形3.向量的加法:(1)定义:求两个向量和的运算,叫做向量的加法. (2)向量的加法法则:①向量加法的三角形法则:B在平面上任取一点A,即这种求向量和的方法,称为向量加法的三角形法则.“首尾相接,首尾连” ②向量加法的平行四边形法则:AC在平面上任取一点O,以OA,OB为邻边作平行四边形OACB, 这种求向量和的方法,称为向量加法的平行四边形法则.③规定:两个向量的和仍然是一个向量.例1:已知向量 和 ,求作向量 + .练习:课本P93页T1,T2.[问题]在你所画图中,找出它们之间有怎样的关系?(3)向量加法中模的性质:当 和 同向时,当 和 反向时,(4)向量加法的交换律和给合律:( )( )向量的加法满足交换律和结合律.练习:课本P94页T3,T4.练习求向量 之和。解:原式= = 例2:长江两岸之间没有大桥的地方,常常通过轮渡进行运输.如图所示,一艘船从长江A点出发,以5km/h的速度和垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小(保留两个有效数字)与方向(用与江水速度间的夹角表示,精确到度).练习在静水中船速为20m/min,水流速度为10m/min,若船从岸边出发,垂直于水流航线到达对岸的,问船行进的方向是_____.向量 表示静水流速, 表示船行进方向, 表示船实际行走路线,垂直于水流方向,所以∠DAC即为所求 课堂小结
1、向量加法的几何意义;
2、交换律和结合律;
3、注意:
当且仅当方向相同时取等号.接12作业:
课本P101页习题
A组T1,(1),(3),(5)
T2,T4(1),(2);
B组T1.备用习题
1、一艘船从A点出发以 的速度向垂直于对岸的方向行驶,船的实际航行的速度的大小为 ,求水流的速度.2、一艘船距对岸 ,以 的速度向垂直于对岸的方向行驶,到达对岸时,船的实际航程为8km,求水流的流速.3、一艘船从A点出发以v1的速度向垂直于对岸的方向行驶,同时河水的流速为v2,船的实际航行的速度大小为 ,方向与水流间的夹角是60°,求v1和v2.4、一艘船以5km/h的速度在行驶,同时河水的流速为2km/h,则船的实际航行速度大小最大是________km/h,最小是_________km/h.
5、已知两个力F1,F2的夹角是直角,且已知它们的合力F与F1的夹角是60°,|F|=10N,求F1和F2的大小.
6、用向量加法证明:两条对角线互相平分的四边形是平行四边形
(1)掌握向量的加法运算,并理解其几何意义;
(2)会用向量加法的三角形法则和平行四边形法则作两个向量的和向量,培养数形结合解决问题的能力;
(3)通过将向量运算与熟悉的数的运算进行类比,使学生掌握向量加法运算的交换律和结合律,并会用它们进行向量计算,渗透类比的数学方法;
教学重点:
会用向量加法的三角形法则和平行四边形法则作两个向量的和向量.
教学难点:理解向量加法的定义.〖教学情境设计〗1.复习:向量的定义以及有关概念.相等向量;平行向量;共线向量;零向量 练习:判断下列命题是否正确(1)两向量相等,则它们的起点相同,终点也相同;(2)若 ,则 或(3)若 ,则A,B,C,D四点是平行四边形的四个顶点 。(4)平行四边形ABCD中一定有(5) 若 ,则(6)若 ∥ , ∥ ,则 ∥2.情景设置: (1)某人从A到B,再从B按原方向到C,则两次的位移和为: (2)某人从A到B,再从B按反方向到C,则两次的位移和为: (3)某车从A到B,再从B改变方向到C,则两次的位移和为: (4)物理学中力的合成用的是____________法则.平行四边形3.向量的加法:(1)定义:求两个向量和的运算,叫做向量的加法. (2)向量的加法法则:①向量加法的三角形法则:B在平面上任取一点A,即这种求向量和的方法,称为向量加法的三角形法则.“首尾相接,首尾连” ②向量加法的平行四边形法则:AC在平面上任取一点O,以OA,OB为邻边作平行四边形OACB, 这种求向量和的方法,称为向量加法的平行四边形法则.③规定:两个向量的和仍然是一个向量.例1:已知向量 和 ,求作向量 + .练习:课本P93页T1,T2.[问题]在你所画图中,找出它们之间有怎样的关系?(3)向量加法中模的性质:当 和 同向时,当 和 反向时,(4)向量加法的交换律和给合律:( )( )向量的加法满足交换律和结合律.练习:课本P94页T3,T4.练习求向量 之和。解:原式= = 例2:长江两岸之间没有大桥的地方,常常通过轮渡进行运输.如图所示,一艘船从长江A点出发,以5km/h的速度和垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小(保留两个有效数字)与方向(用与江水速度间的夹角表示,精确到度).练习在静水中船速为20m/min,水流速度为10m/min,若船从岸边出发,垂直于水流航线到达对岸的,问船行进的方向是_____.向量 表示静水流速, 表示船行进方向, 表示船实际行走路线,垂直于水流方向,所以∠DAC即为所求 课堂小结
1、向量加法的几何意义;
2、交换律和结合律;
3、注意:
当且仅当方向相同时取等号.接12作业:
课本P101页习题
A组T1,(1),(3),(5)
T2,T4(1),(2);
B组T1.备用习题
1、一艘船从A点出发以 的速度向垂直于对岸的方向行驶,船的实际航行的速度的大小为 ,求水流的速度.2、一艘船距对岸 ,以 的速度向垂直于对岸的方向行驶,到达对岸时,船的实际航程为8km,求水流的流速.3、一艘船从A点出发以v1的速度向垂直于对岸的方向行驶,同时河水的流速为v2,船的实际航行的速度大小为 ,方向与水流间的夹角是60°,求v1和v2.4、一艘船以5km/h的速度在行驶,同时河水的流速为2km/h,则船的实际航行速度大小最大是________km/h,最小是_________km/h.
5、已知两个力F1,F2的夹角是直角,且已知它们的合力F与F1的夹角是60°,|F|=10N,求F1和F2的大小.
6、用向量加法证明:两条对角线互相平分的四边形是平行四边形
