第一章 三角形 3 探索三角形全等的条件 第1课时 “边边边”(含答案)
文档属性
| 名称 | 第一章 三角形 3 探索三角形全等的条件 第1课时 “边边边”(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-24 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第一章 三角形
3 探索三角形全等的条件
第1课时 “边边边”
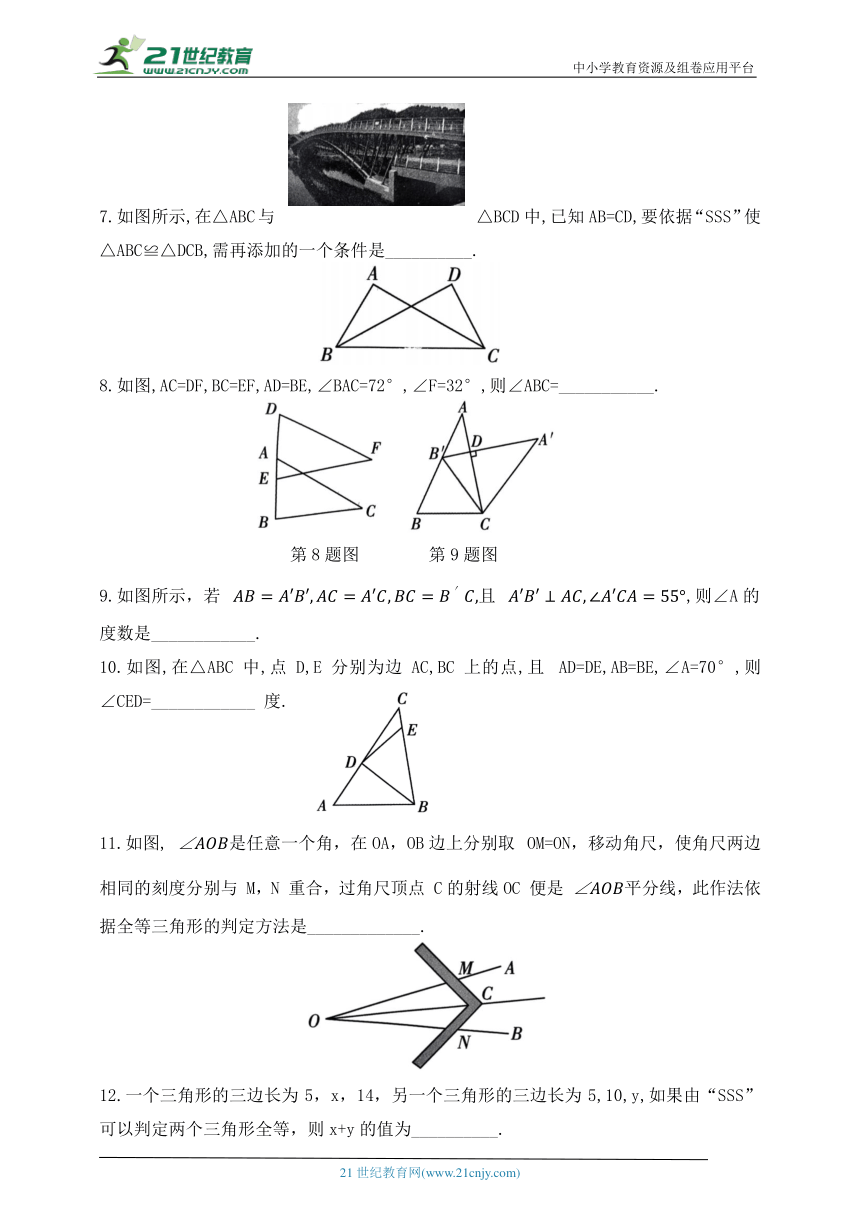
1.下列四个三角形中,与如图所示的三角形全等的是 ( )
2.如图,一个六边形形状的木框,为使其稳定,工人师傅至少需要加固多少根木条( )
A.2 B.3 C.4 D.5
第2题图 第3题图
3. 如图, ∠BAD=46°,则∠ACD 的度数是 ( )
A.120° B.125° C.127° D.104°
4.如图,已知AC=FE,BC=DE,点A,D,B,F在一条直线上,要利用“SSS”证明△ABC≌△FDE,还可以添加的一个条件是 ( )
A. AD=FB B. DE=BD C. BF=DB D.以上都不对
第4题图 第5题图
5.如图,已知 下列结论:①∠BAC=∠DCA ②∠ACB=∠CAD ③AB∥CD,BC∥DA.其中正确的结论有( )
A.0个 B.1个 C.2个 D.3个
6.如图,钢架桥的设计中采用了三角形的结构,其数学道理是__________________.
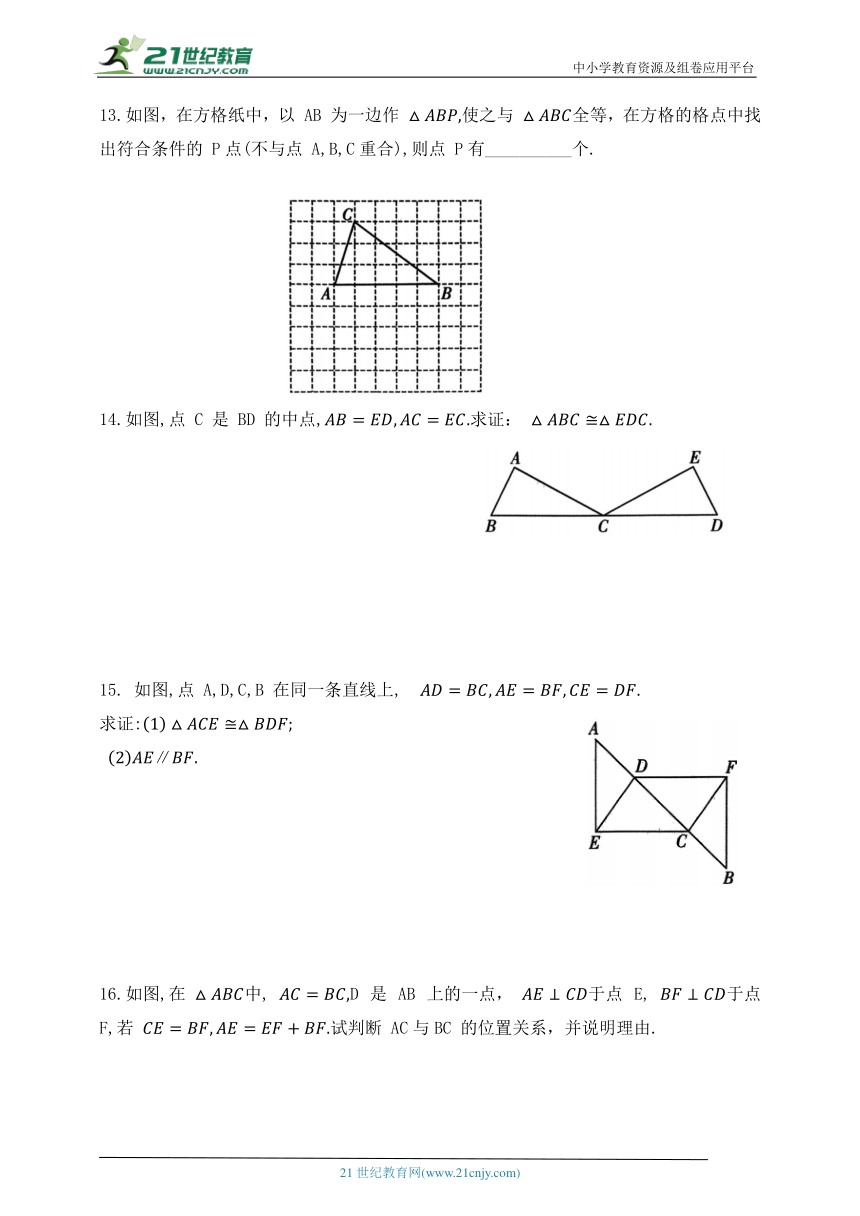
7.如图所示,在△ABC与△BCD中,已知AB=CD,要依据“SSS”使△ABC≌△DCB,需再添加的一个条件是__________.
8.如图,AC=DF,BC=EF,AD=BE,∠BAC=72°,∠F=32°,则∠ABC=___________.
第8题图 第9题图
9.如图所示,若 且 ,则∠A的
度数是____________.
10.如图,在△ABC中,点D,E分别为边AC,BC上的点,且 AD=DE,AB=BE,∠A=70°,则 ∠CED=____________ 度.
11.如图, 是任意一个角,在OA,OB边上分别取 OM=ON,移动角尺,使角尺两边相同的刻度分别与 M,N 重合,过角尺顶点 C的射线OC 便是 平分线,此作法依据全等三角形的判定方法是_____________.
12.一个三角形的三边长为5,x,14,另一个三角形的三边长为5,10,y,如果由“SSS”可以判定两个三角形全等,则x+y的值为__________.
13.如图,在方格纸中,以 AB 为一边作 使之与 全等,在方格的格点中找出符合条件的 P点(不与点 A,B,C重合),则点 P有__________个.
14.如图,点 C 是 BD 的中点,求证:
15. 如图,点 A,D,C,B 在同一条直线上,
求证:
∥
16.如图,在 中, D 是 AB 上的一点, 于点 E, 于点F,若 试判断 AC与BC 的位置关系,并说明理由.
参考答案
1. B 2. B 3. C 4. A 5. D
6.三角形具有稳定性
9.35° 10.110 11.“SSS” 12.24
13.3 解析:如图所示,
与 全等,共有 3个点.
14.证明:因为 C 是 BD 的中点,所以 BC=CD,
在△ABC和△EDC中, 所以△ABC≌△EDC(SSS).
15.证明:(1)因为 AD=BC,所以AC=BD,
在△ACE 与△BDF中,
所以△ACE≌△BDF(SSS);
(2)因为△ACE≌△BDF,所以∠A=∠B,所以 AE∥BF.
16.解:AC⊥BC;
理由:因为 AE⊥CD,BF⊥CD,所以∠AEC=∠BFC=90°,所以∠CAE+∠ACE=90°,
因为CF=CE+EF,CE=BF,所以CF=EF+BF,
因为AE=EF+BF,所以 AE=CF,
在 Rt△ACE 和 Rt△CBF 中, 所以 Rt△ACE≌Rt△CBF(SSS),
所以∠BCF=∠CAE,
所以∠ACB =∠BCF+∠ACE=∠CAE+∠ACE=90°,
所以 AC⊥BC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一章 三角形
3 探索三角形全等的条件
第1课时 “边边边”
1.下列四个三角形中,与如图所示的三角形全等的是 ( )
2.如图,一个六边形形状的木框,为使其稳定,工人师傅至少需要加固多少根木条( )
A.2 B.3 C.4 D.5
第2题图 第3题图
3. 如图, ∠BAD=46°,则∠ACD 的度数是 ( )
A.120° B.125° C.127° D.104°
4.如图,已知AC=FE,BC=DE,点A,D,B,F在一条直线上,要利用“SSS”证明△ABC≌△FDE,还可以添加的一个条件是 ( )
A. AD=FB B. DE=BD C. BF=DB D.以上都不对
第4题图 第5题图
5.如图,已知 下列结论:①∠BAC=∠DCA ②∠ACB=∠CAD ③AB∥CD,BC∥DA.其中正确的结论有( )
A.0个 B.1个 C.2个 D.3个
6.如图,钢架桥的设计中采用了三角形的结构,其数学道理是__________________.
7.如图所示,在△ABC与△BCD中,已知AB=CD,要依据“SSS”使△ABC≌△DCB,需再添加的一个条件是__________.
8.如图,AC=DF,BC=EF,AD=BE,∠BAC=72°,∠F=32°,则∠ABC=___________.
第8题图 第9题图
9.如图所示,若 且 ,则∠A的
度数是____________.
10.如图,在△ABC中,点D,E分别为边AC,BC上的点,且 AD=DE,AB=BE,∠A=70°,则 ∠CED=____________ 度.
11.如图, 是任意一个角,在OA,OB边上分别取 OM=ON,移动角尺,使角尺两边相同的刻度分别与 M,N 重合,过角尺顶点 C的射线OC 便是 平分线,此作法依据全等三角形的判定方法是_____________.
12.一个三角形的三边长为5,x,14,另一个三角形的三边长为5,10,y,如果由“SSS”可以判定两个三角形全等,则x+y的值为__________.
13.如图,在方格纸中,以 AB 为一边作 使之与 全等,在方格的格点中找出符合条件的 P点(不与点 A,B,C重合),则点 P有__________个.
14.如图,点 C 是 BD 的中点,求证:
15. 如图,点 A,D,C,B 在同一条直线上,
求证:
∥
16.如图,在 中, D 是 AB 上的一点, 于点 E, 于点F,若 试判断 AC与BC 的位置关系,并说明理由.
参考答案
1. B 2. B 3. C 4. A 5. D
6.三角形具有稳定性
9.35° 10.110 11.“SSS” 12.24
13.3 解析:如图所示,
与 全等,共有 3个点.
14.证明:因为 C 是 BD 的中点,所以 BC=CD,
在△ABC和△EDC中, 所以△ABC≌△EDC(SSS).
15.证明:(1)因为 AD=BC,所以AC=BD,
在△ACE 与△BDF中,
所以△ACE≌△BDF(SSS);
(2)因为△ACE≌△BDF,所以∠A=∠B,所以 AE∥BF.
16.解:AC⊥BC;
理由:因为 AE⊥CD,BF⊥CD,所以∠AEC=∠BFC=90°,所以∠CAE+∠ACE=90°,
因为CF=CE+EF,CE=BF,所以CF=EF+BF,
因为AE=EF+BF,所以 AE=CF,
在 Rt△ACE 和 Rt△CBF 中, 所以 Rt△ACE≌Rt△CBF(SSS),
所以∠BCF=∠CAE,
所以∠ACB =∠BCF+∠ACE=∠CAE+∠ACE=90°,
所以 AC⊥BC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
