第一章 三角形 3 探索全等的条件 第3课时 “边角边”(含答案)
文档属性
| 名称 | 第一章 三角形 3 探索全等的条件 第3课时 “边角边”(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-24 13:18:38 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第一章 三角形
3 探索全等的条件
第3课时 “边角边”
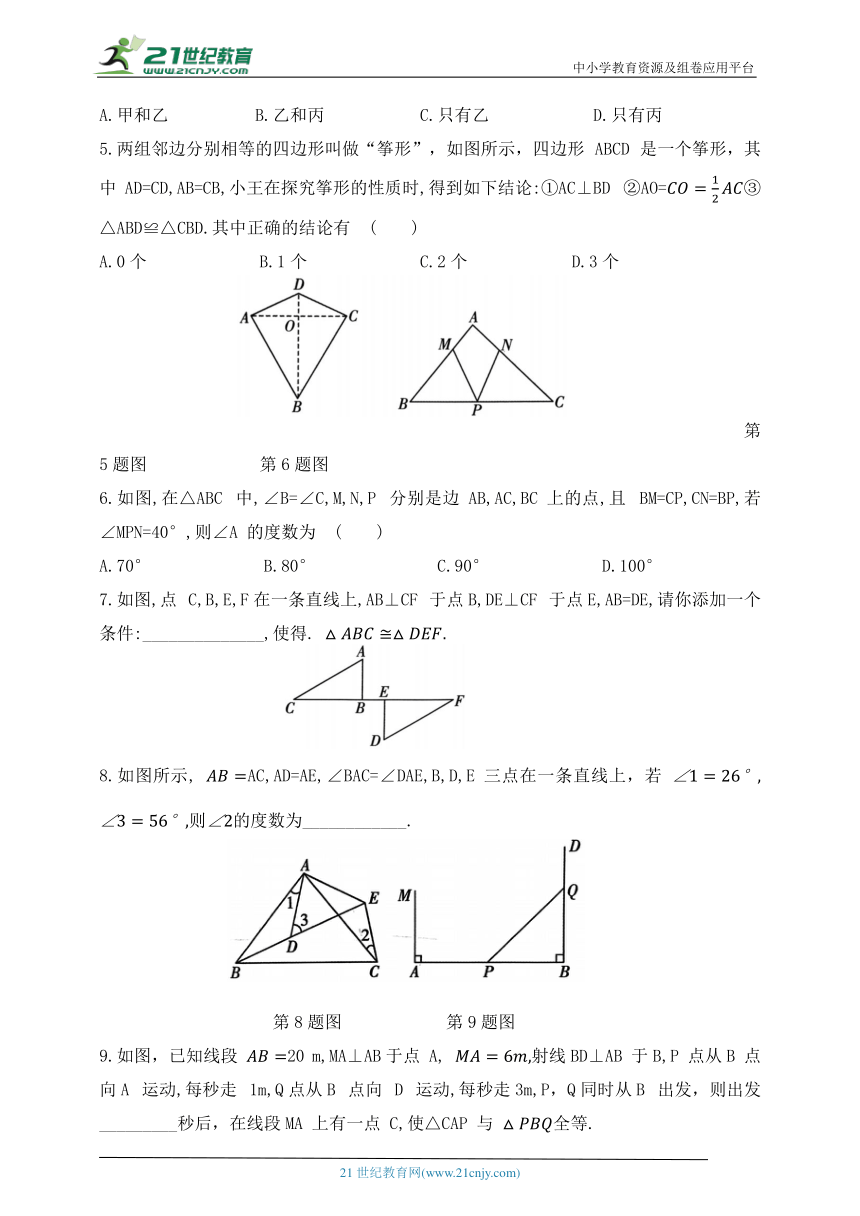
1.如图,工人师傅设计了一种测零件内径 AB 的卡钳,卡钳交叉点 O 为的中点,只要量出 的长度,就可以知道该零件内径 AB的长度.依据的数学基本事实是( )
A.两边及其夹角分别相等的两个三角形全等
B.两角及其夹边分别相等的两个三角形全等
C.两条直线被一组平行线所截,所的对应线段成比例
D.两点之间线段最短
2.如图,AC 和BD 相交于点O,OA=OC,OB=OD,下列说法错误的是 ( )
A. AB∥CD B. AB=CD C. AB≠CD但是AB∥CD D. AB=CD 且AB∥CD
第2题图 第3题图
3.如图,BD=BC,BE=CA,∠DBE=∠C=62°,∠BDE=75°,则∠AFD的度数等于( )
A.30° B.32° C.33° D.35°
4.如图所示,已知 的五个元素,右侧甲、乙、丙三个三角形中和 全等的图形是 ( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
5.两组邻边分别相等的四边形叫做“筝形”,如图所示,四边形 ABCD 是一个筝形,其中AD=CD,AB=CB,小王在探究筝形的性质时,得到如下结论:①AC⊥BD ②AO=③△ABD≌△CBD.其中正确的结论有 ( )
A.0个 B.1个 C.2个 D.3个
第5题图 第6题图
6.如图,在△ABC 中,∠B=∠C,M,N,P 分别是边AB,AC,BC上的点,且 BM=CP,CN=BP,若 ∠MPN=40°,则∠A 的度数为 ( )
A.70° B.80° C.90° D.100°
7.如图,点 C,B,E,F在一条直线上,AB⊥CF 于点B,DE⊥CF 于点E,AB=DE,请你添加一个条件:______________,使得.
8.如图所示, AC,AD=AE,∠BAC=∠DAE,B,D,E三点在一条直线上,若 则的度数为____________.
第8题图 第9题图
9.如图,已知线段 20 m,MA⊥AB于点 A, 射线BD⊥AB 于B,P 点从B 点向A 运动,每秒走 1m,Q点从B 点向 D 运动,每秒走3m,P,Q同时从B 出发,则出发_________秒后,在线段MA 上有一点 C,使△CAP 与 全等.
10. 如图,AB = 4 cm,AC=BD = 3cm, ∠CAB=∠DBA,点P 在线段 AB 上以1 cm/s的速度由点A向点B运动.同时,点Q在线段BD上由点B向点D运动,设运动时间为t(s) ,则当△ACP与全等时,点 Q的运动速度为_________.
11.如图,OA=OC,OB=OD, ∠AOD=∠COB.
求证:AB=CD.
12.如图,在△ABC 中,∠B=50°,∠C=20°.过点 A作AE⊥BC,垂足为E,延长 EA至点 D,使 AD=AC.在边 AC 上截取AF=AB,连接DF.
求证:DF=CB.
13. AD 是△ABC 中BC 边上的中线,若 AB=4,AC=6,则AD 的取值范围是 ( )
14. 如图,已知∠E=∠F=90°,EB=FC,AE=AF,下列结论:①EM=FN ②CM=EM ③∠FAN=∠EAM ④△ACN≌△ABM.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
第14题图 第15题图
15.如图所示,在四边形ABCD 中,∠B=∠D,AB=8,CD=5,延长BC交AD于点E,若CE⊥AD,AE=
ED,则四边形 ABCD的面积等于 ( )
A.10 B.20 C.30 D.40
参考答案
1. A 2. C 3. B 4. B 5. D 6. D
7.(示例)BC=EF
8.30°
9.5 解析:由题意可知 PB=t m,AP=(20-t)m,BQ=3tm,
①当△APC≌△BQP 时,AP=BQ,即20-t=3t,解得t=5,
此时AC=BP=5m,符合题意;
②当△APC≌△BPQ时,AP=BP,即20-t=t,解得t=10,
此时AC=BQ=30m,
因为 MA=6<30,故 t=10不符合题意.
10.1 cm/s或
解析:设点 Q的运动速度是x cm/s,
因为∠CAB=∠DBA,所以△ACP 与△BPQ全等,有两种情况:
①AP=BP,AC=BQ,则1·t=4-1·t,3=tx,解得
②AP=BQ,AC=BP,则1·t=tx,4-1·t=3,解得 t=1,x=1;
综上所述,点 Q 的运动速度为 1 cm/s 或
11.证明:因为∠AOD=∠COB,所以∠AOD-∠BOD=∠COB-∠BOD,即∠AOB=∠COD.
在△AOB 和△COD中, 所以△AOB≌△COD(SAS),所以AB=CD.
12.证明:因为在△ABC 中,∠B=50°,∠C=20°,所以∠CAB=180°-∠B-∠C=110°.
因为 AE⊥BC,所以∠AEC=90°,
所以
所以
在 和 中,
所以 所以
13. C 解析:如图,在 中,AD 是 BC 边上的中线,延长 AD 到点 E 使 连接CE,
因为CD=BD,∠CDE=∠BDA,DE=DA,所以△CDE≌△BDA(SAS),
所以CE=AB=4,
因为在△ACE中,
14. C 解析:∠E=∠F=90°,EB=FC,AE=AF,
所以△AEB≌△AFC(SAS),所以∠EAB=∠FAC,所以∠FAN=∠EAM,
故③正确;
因为∠E=∠F=90°,AE=AF,∠FAN=∠EAM.
所以△AEM≌△AFN(ASA),所以 EM=FN,
故①正确;
由△AEM≌△AFN(ASA),得到 EM=FN,得不到 EM=CM,
故②错误;
因为△AEB≌△AFC,所以AC=AB,
因为∠C=∠B,∠CAN=∠BAM,所以△ACN≌△ABM(ASA),
故④正确;
所以正确的有 3个.
15. B 解析:如图,延长 CE 到点 K,使 KE=CE,连接AK,
因为 所以
所以
又因为 所以
由 知
所以 即
所以
所以
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一章 三角形
3 探索全等的条件
第3课时 “边角边”
1.如图,工人师傅设计了一种测零件内径 AB 的卡钳,卡钳交叉点 O 为的中点,只要量出 的长度,就可以知道该零件内径 AB的长度.依据的数学基本事实是( )
A.两边及其夹角分别相等的两个三角形全等
B.两角及其夹边分别相等的两个三角形全等
C.两条直线被一组平行线所截,所的对应线段成比例
D.两点之间线段最短
2.如图,AC 和BD 相交于点O,OA=OC,OB=OD,下列说法错误的是 ( )
A. AB∥CD B. AB=CD C. AB≠CD但是AB∥CD D. AB=CD 且AB∥CD
第2题图 第3题图
3.如图,BD=BC,BE=CA,∠DBE=∠C=62°,∠BDE=75°,则∠AFD的度数等于( )
A.30° B.32° C.33° D.35°
4.如图所示,已知 的五个元素,右侧甲、乙、丙三个三角形中和 全等的图形是 ( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
5.两组邻边分别相等的四边形叫做“筝形”,如图所示,四边形 ABCD 是一个筝形,其中AD=CD,AB=CB,小王在探究筝形的性质时,得到如下结论:①AC⊥BD ②AO=③△ABD≌△CBD.其中正确的结论有 ( )
A.0个 B.1个 C.2个 D.3个
第5题图 第6题图
6.如图,在△ABC 中,∠B=∠C,M,N,P 分别是边AB,AC,BC上的点,且 BM=CP,CN=BP,若 ∠MPN=40°,则∠A 的度数为 ( )
A.70° B.80° C.90° D.100°
7.如图,点 C,B,E,F在一条直线上,AB⊥CF 于点B,DE⊥CF 于点E,AB=DE,请你添加一个条件:______________,使得.
8.如图所示, AC,AD=AE,∠BAC=∠DAE,B,D,E三点在一条直线上,若 则的度数为____________.
第8题图 第9题图
9.如图,已知线段 20 m,MA⊥AB于点 A, 射线BD⊥AB 于B,P 点从B 点向A 运动,每秒走 1m,Q点从B 点向 D 运动,每秒走3m,P,Q同时从B 出发,则出发_________秒后,在线段MA 上有一点 C,使△CAP 与 全等.
10. 如图,AB = 4 cm,AC=BD = 3cm, ∠CAB=∠DBA,点P 在线段 AB 上以1 cm/s的速度由点A向点B运动.同时,点Q在线段BD上由点B向点D运动,设运动时间为t(s) ,则当△ACP与全等时,点 Q的运动速度为_________.
11.如图,OA=OC,OB=OD, ∠AOD=∠COB.
求证:AB=CD.
12.如图,在△ABC 中,∠B=50°,∠C=20°.过点 A作AE⊥BC,垂足为E,延长 EA至点 D,使 AD=AC.在边 AC 上截取AF=AB,连接DF.
求证:DF=CB.
13. AD 是△ABC 中BC 边上的中线,若 AB=4,AC=6,则AD 的取值范围是 ( )
14. 如图,已知∠E=∠F=90°,EB=FC,AE=AF,下列结论:①EM=FN ②CM=EM ③∠FAN=∠EAM ④△ACN≌△ABM.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
第14题图 第15题图
15.如图所示,在四边形ABCD 中,∠B=∠D,AB=8,CD=5,延长BC交AD于点E,若CE⊥AD,AE=
ED,则四边形 ABCD的面积等于 ( )
A.10 B.20 C.30 D.40
参考答案
1. A 2. C 3. B 4. B 5. D 6. D
7.(示例)BC=EF
8.30°
9.5 解析:由题意可知 PB=t m,AP=(20-t)m,BQ=3tm,
①当△APC≌△BQP 时,AP=BQ,即20-t=3t,解得t=5,
此时AC=BP=5m,符合题意;
②当△APC≌△BPQ时,AP=BP,即20-t=t,解得t=10,
此时AC=BQ=30m,
因为 MA=6<30,故 t=10不符合题意.
10.1 cm/s或
解析:设点 Q的运动速度是x cm/s,
因为∠CAB=∠DBA,所以△ACP 与△BPQ全等,有两种情况:
①AP=BP,AC=BQ,则1·t=4-1·t,3=tx,解得
②AP=BQ,AC=BP,则1·t=tx,4-1·t=3,解得 t=1,x=1;
综上所述,点 Q 的运动速度为 1 cm/s 或
11.证明:因为∠AOD=∠COB,所以∠AOD-∠BOD=∠COB-∠BOD,即∠AOB=∠COD.
在△AOB 和△COD中, 所以△AOB≌△COD(SAS),所以AB=CD.
12.证明:因为在△ABC 中,∠B=50°,∠C=20°,所以∠CAB=180°-∠B-∠C=110°.
因为 AE⊥BC,所以∠AEC=90°,
所以
所以
在 和 中,
所以 所以
13. C 解析:如图,在 中,AD 是 BC 边上的中线,延长 AD 到点 E 使 连接CE,
因为CD=BD,∠CDE=∠BDA,DE=DA,所以△CDE≌△BDA(SAS),
所以CE=AB=4,
因为在△ACE中,
14. C 解析:∠E=∠F=90°,EB=FC,AE=AF,
所以△AEB≌△AFC(SAS),所以∠EAB=∠FAC,所以∠FAN=∠EAM,
故③正确;
因为∠E=∠F=90°,AE=AF,∠FAN=∠EAM.
所以△AEM≌△AFN(ASA),所以 EM=FN,
故①正确;
由△AEM≌△AFN(ASA),得到 EM=FN,得不到 EM=CM,
故②错误;
因为△AEB≌△AFC,所以AC=AB,
因为∠C=∠B,∠CAN=∠BAM,所以△ACN≌△ABM(ASA),
故④正确;
所以正确的有 3个.
15. B 解析:如图,延长 CE 到点 K,使 KE=CE,连接AK,
因为 所以
所以
又因为 所以
由 知
所以 即
所以
所以
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
