苏科版九年级数学上册试题 第2章 对称图形—圆 章节检测卷 (含详解)
文档属性
| 名称 | 苏科版九年级数学上册试题 第2章 对称图形—圆 章节检测卷 (含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1014.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-24 21:31:38 | ||
图片预览


文档简介
第2章《 对称图形—圆》章节检测卷
一.选择题(每小题2分,共12分)
1.如图,CD是的直径,弦AB⊥CD于点G,直线EF与相切与点D,则下列结论中不一定正确的是( )
A. AG=BG B. AB∥EF C. AD∥BC D. ∠ABC=∠ADC
2.如图,是⊙的直径,是⊙上两点,若,则的度数是( )
A. B. C. D.
3.如图,已知⊙O的半径为5,弦AB、CD所对的圆心角分别是∠AOB、∠COD,若∠AOB与∠COD互补,弦CD=6,则点O到弦AB的距离为( )
A.6 B.8 C.3 D.4
4.如图,在 O中,,BC=6.AC=3,I是△ABC的内心,则线段OI的值为( )
A.1 B.3 C.5 D.
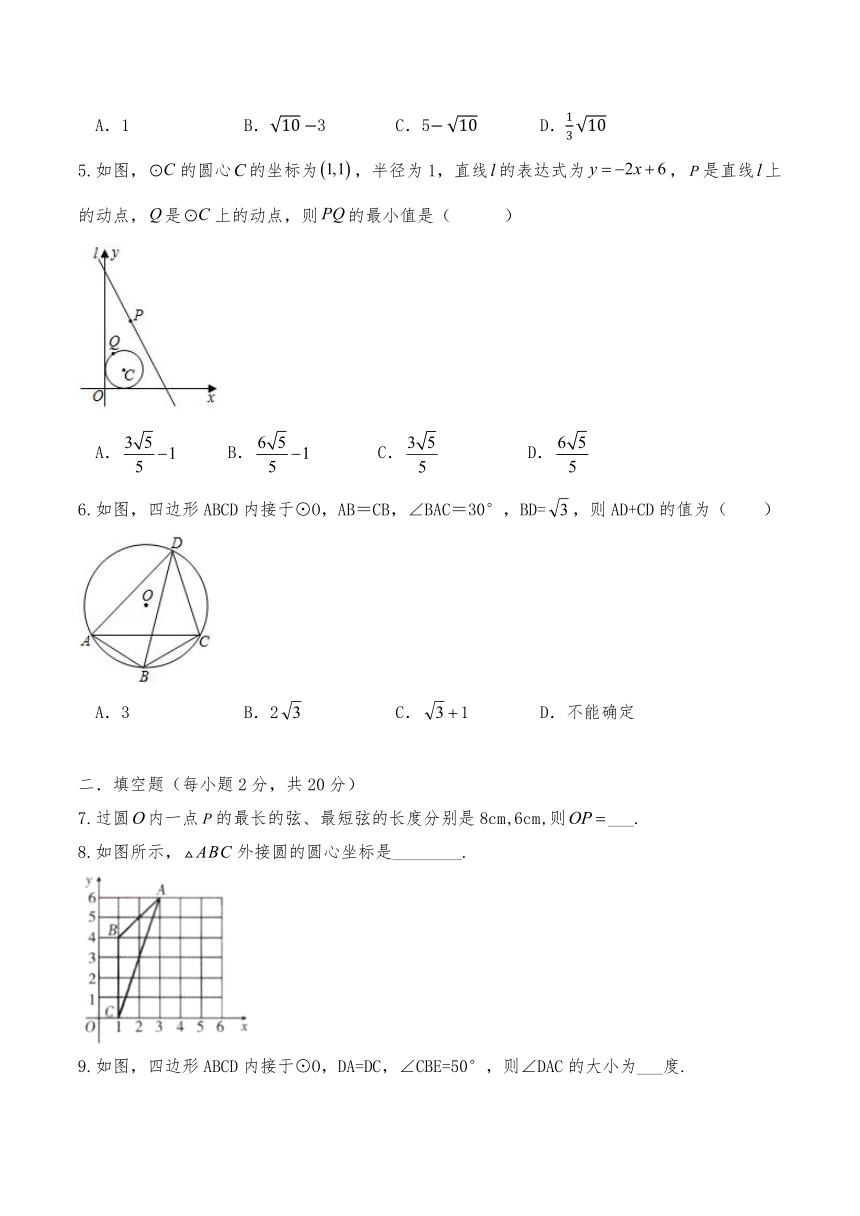
5.如图,的圆心的坐标为,半径为1,直线的表达式为,是直线上的动点,是上的动点,则的最小值是( )
A. B. C. D.
6.如图,四边形ABCD内接于⊙O,AB=CB,∠BAC=30°,BD=,则AD+CD的值为( )
A.3 B.2 C.1 D.不能确定
二.填空题(每小题2分,共20分)
7.过圆内一点的最长的弦、最短弦的长度分别是8cm,6cm,则___.
8.如图所示,外接圆的圆心坐标是________.
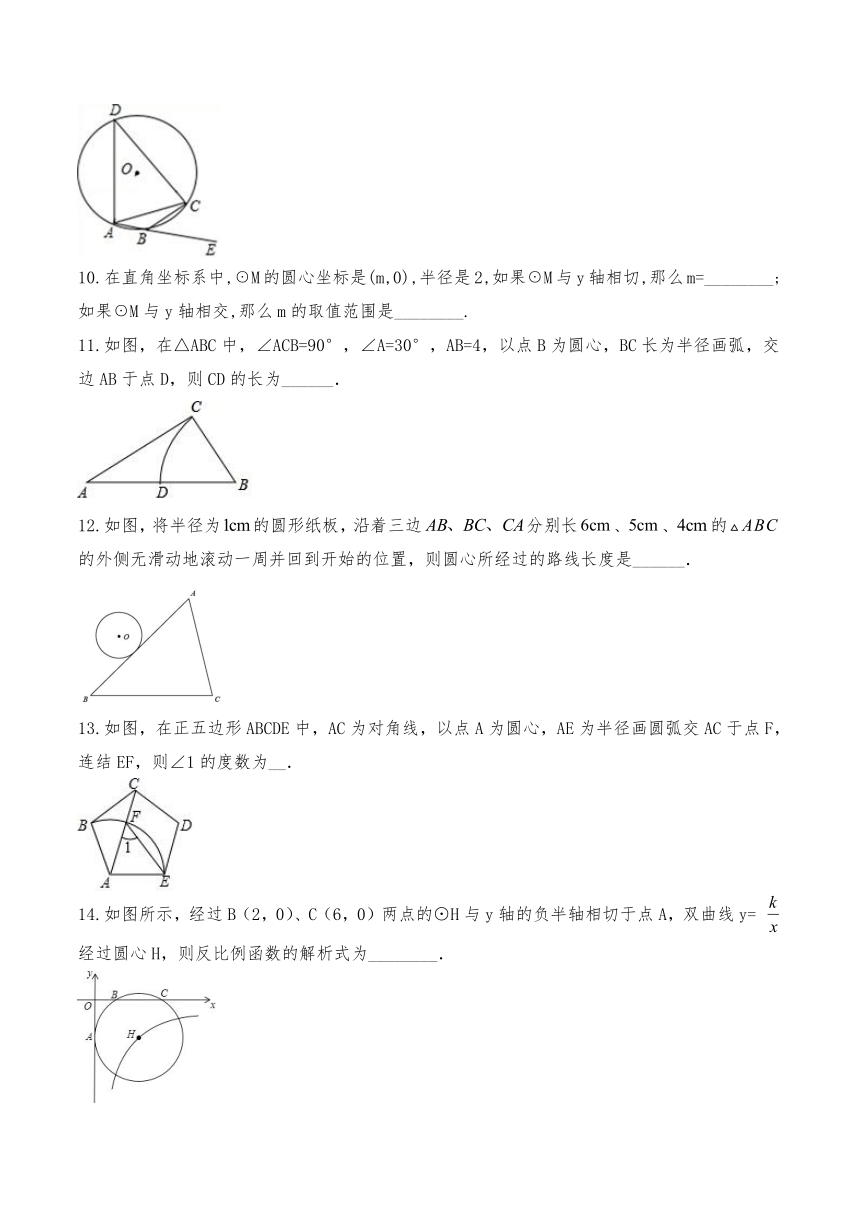
9.如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为___度.
10.在直角坐标系中,☉M的圆心坐标是(m,0),半径是2,如果☉M与y轴相切,那么m=________;如果☉M与y轴相交,那么m的取值范围是________.
11.如图,在△ABC中,∠ACB=90°,∠A=30°,AB=4,以点B为圆心,BC长为半径画弧,交边AB于点D,则CD的长为______.
12.如图,将半径为的圆形纸板,沿着三边分别长、、的的外侧无滑动地滚动一周并回到开始的位置,则圆心所经过的路线长度是______.
13.如图,在正五边形ABCDE中,AC为对角线,以点A为圆心,AE为半径画圆弧交AC于点F,连结EF,则∠1的度数为__.
14.如图所示,经过B(2,0)、C(6,0)两点的⊙H与y轴的负半轴相切于点A,双曲线y= 经过圆心H,则反比例函数的解析式为________.
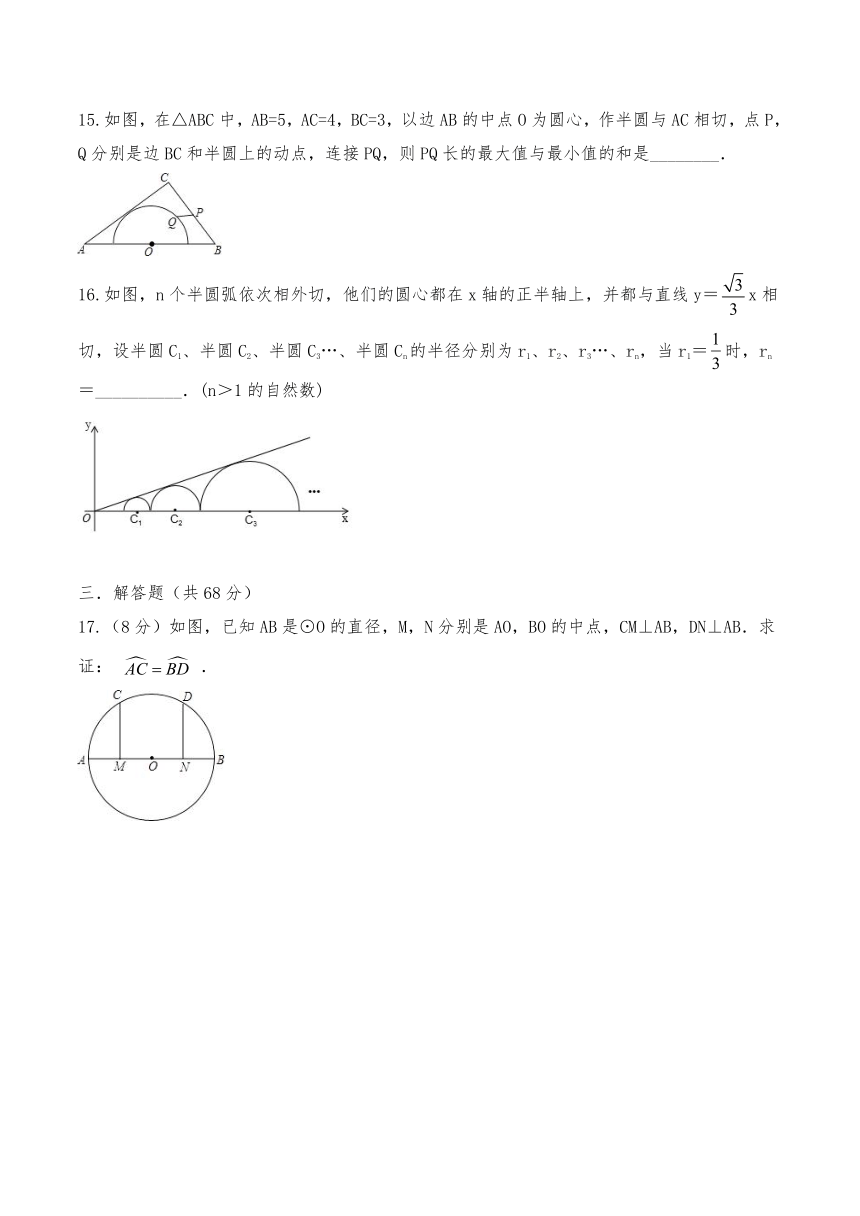
15.如图,在△ABC中,AB=5,AC=4,BC=3,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是________.
16.如图,n个半圆弧依次相外切,他们的圆心都在x轴的正半轴上,并都与直线y=x相切,设半圆C1、半圆C2、半圆C3…、半圆Cn的半径分别为r1、r2、r3…、rn,当r1=时,rn=__________.(n>1的自然数)
三.解答题(共68分)
17.(8分)如图,已知AB是⊙O的直径,M,N分别是AO,BO的中点,CM⊥AB,DN⊥AB.求证: .
18.(8分)如图,已知AB为⊙O的直径,点C为半圆ACB上的动点(不与A、B两点重合),过点C作弦CD⊥AB,∠OCD的平分线交圆于点P,则点P的位置有何规律?请证明你的结论.
19.(10分)如图,在Rt△ABC中,∠ABC=90°,点F为AC中点,⊙O经过点B,F,且与AC交于点D,与AB交于点E,与BC交于点G,连结BF,DE,弧EFG的长度为(1+)π.
(1)求⊙O的半径;
(2)若DE∥BF,且AE=a,DF=2+﹣a,请判断圆心O和直线BF的位置关系,并说明理由.
20.(10分)如图,已知P是外一点.用两种不同的方法过点P作的一条切线.要求:
(1)用直尺和圆规作图;
(2)保留作图的痕迹,写出必要的文字说明.
21.(10分)如图,I是△ABC的内心,AI的延长线交边BC于点D,交△ABC的外接圆于点E.
(1)BE与IE相等吗?请说明理由.
(2)连接BI,CI,CE,若∠BED=∠CED=60°,猜想四边形BECI是何种特殊四边形,并证明你的猜想.
22.(10分)已知△ABC中,AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心、OB为半径作圆,且⊙O过A点.
(1)如图①,若⊙O的半径为5,求线段OC的长;
(2)如图②,过点A作AD∥BC交⊙O于点D,连接BD,求的值.
23.(12分)如图1,中,,半径为r的经过点A且与相切,切点M在线段上(包含点M与点B、C重合的情况).
(1)半径r的最小值等于________:
(2)设,求半径r关于x的函数表达式;
(3)当时,请在图2中作出点M及满足条件的.
(要求:尺规作图,不写作法,保留作图痕迹,并用2B铅笔或黑色水笔加黑加粗)
答案
一.选择题
1.C
【解析】解:(A)∵CD是的直径,弦AB⊥CD于点G,∴由垂径定理可知:AG=BG.结论正确.
(B)∵直线EF与相切与点D,∴EF⊥AD.∴AB∥EF.结论正确.
(C)要AD∥BC,即要∠ABC=∠BAD,由圆周角定理,∠ABC=∠ADC,即要∠BAD =∠ADC,即要AG=DG,但没此条件.结论错误.
(D)∵∠ABC和∠ADC是同弧所对的圆周角,∴∠ABC=∠ADC.结论正确.
故选:C.
2.C
【解析】解:连接AC、AD,∴∠ADC=∠ABC=40°
∵是⊙的直径∴∠ADB=90°,∴∠BDC=∠ADB-∠ADC=90°-40°=50°.
故选C.
3.C
【解析】延长CO交⊙O于E,连接DE,过O作OF⊥DE于F,OH⊥CD于H,OG⊥AB于G,线段OG的长是点O到弦AB的距离,
∵∠COD和∠DOE互补,∠COD和∠AOB互补,∴∠DOE=∠AOB,
∴DE=AB,OF=OG,
∵OH⊥DC,CD=6,OH过O,∴DH=HCDC=3,∠OHD=∠OHC=90°,
由勾股定理得:OH4,
∵OC=OE,DH=HC,OH=4,∴DE=2OH=8,
∵OF⊥DE,OF过O,∴DF=EF=DE=4,
在Rt△DFO中,由勾股定理得:OF3,∴OG=OF=3,
即点O到AB的距离是3,
故选C.
4.C
【解析】如图,连接AO,延长AO交BC于H,连接OB.
∵,∴AB=AC,AH⊥BC,∴BH=CH=3,
∴AH9,
设OA=OB=x,
在Rt△BOH中,∵OB2=OH2+BH2,
∴x2=(9﹣x)2+32,∴x=5,∴OH=AHAO=9﹣5=4,
∵S△ABC BC AH (AB+AC+BC) IH,∴IH1,∴OI=OH﹣IH=4﹣(1)=5-,
故选C.
5.A
【解析】解:过点作直线,交圆于点,此时的值最小,连接、,作于,于,
∵,∴,,∴,,∴,
∵四边形是正方形,∴,∴,,
设,,则,
∵,,
∴,,
解得:,
∵的半径为1,∴,
故选:A.
6.A
【解析】如图,过点B作BE⊥AD于E,BF⊥DC交DC的延长线于F.
∵AB=BC,∴,∴∠BDE=∠BDF,
∵∠DEB=∠DFB=90°,DB=DB,
∴△BDE≌△BDF(AAS),∴BE=BF,DE=DF,
∵∠AEB=∠F=90°,BA=BC,BE=BF,∴Rt△BEA≌Rt△BFC(HL),∴AE=CF,
∴AD+DC=DE+AE+DF﹣CF=2DF,
∵∠BDF=∠BAC=30°,BD,∴BFBD,
∴DF,∴DA+DC=3,
故选A.
二.填空题
7.
【解析】如图所示,直径AB⊥弦CD于点P,根据题意,得AB=8cm,CD=6cm,OC=AB=4cm,
∵CD⊥AB,∴CP=CD=3cm.根据勾股定理,得OP=(cm),
8.
【解析】解:作AB和BC的垂直平分线,它们的交点P为△ABC外接圆圆心,
∵ P点坐标是P(5,2),∴ 外接圆的圆心坐标是(5,2).
故答案为(5,2).
9.65
【解析】解:∵∠CBE=50°,∴∠ABC=180°﹣∠CBE=180°﹣50°=130°.∵四边形ABCD为⊙O的内接四边形,∴∠D=180°﹣∠ABC=180°﹣130°=50°.∵DA=DC,∴∠DAC==65°.故答案为65.
10.±2 -2【解析】∵☉M的圆心坐标是(m,0),∴圆心在x轴上,
∵☉M与y轴相切,∴圆心到y轴的距离等于该圆的半径,,故m=±2,
∵☉M与y轴相交,∴圆心到y轴的距离小于等于2,即圆心到y轴的距离|m|<2,∴-2故答案为±2 ;-211.2
【解析】解:连接CD,
∵∠ACB=90°,∠A=30°,AB=4,∴∠B=60°,BC=AB=2,
∵以点B为圆心,BC长为半径画弧,交边AB于点D,
∴△BCD是等边三角形,∴CD=BC=2,
故答案为2.
12.
【解析】圆在三角形的三个角的顶点处旋转的角度是:360°,
则旋转的路线长是:l==,
圆心O所经过的路线的长度=6+5+4+=15+.
故答案为:15+.
13.54°
【解析】解:∵五边形ABCDE是正五边形,∴∠EAB=∠ABC==108°,
∵BA=BC,∴∠BAC=∠BCA==36°,∴∠EAF=108°﹣36°=72°,
∵以点A为圆心,AE为半径画圆弧交AC于点F,∴AE=AF,∴∠1==54°.
故答案为:54°.
14.y=﹣
【解析】过H作HE⊥BC于点E,连接BH,AH,如图,
∵B(2,0),C(6,0),∴BC=4,∴BE=BC=2,∴OE=OB+BE=2+2=4,
又 ⊙H与y轴切于点A,∴AH⊥y轴,∴AH=OE=4,∴BH=4,
在Rt△BEH中,BE=2,BH=4,∴HE==2,∴H点坐标为(4,-2),
∵y=经过圆心H,∴k=-8,
∴反比例函数的解析式为y=﹣,
故答案为y=﹣.
15.4.5
【解析】如图,设⊙O与AC相切于点E,连接OE,作OP1⊥BC垂足为P1交⊙O于Q1,此时垂线段OP1最短,P1Q1最小值为OP1﹣OQ1 ,
∵AB=5,AC=4,BC=3,∴AB2=AC2+BC2 , ∴∠C=90°,
∵∠OP1B=90°,∴OP1∥AC
∵AO=OB,∴P1C=P1B,∴OP1= AC=2,
∴P1Q1最小值为OP1﹣OQ1=0.5,
如图,当Q2在AB边上时,P2与B重合时,P2Q2经过圆心,经过圆心的弦最长,
P2Q2最大值=2.5+1.5=4,
∴PQ长的最大值与最小值的和是4.5.
故答案为4.5.
16.3n 2
【解析】解:过点Cn作CnAn⊥直线于点An,如图所示,
∵直线解析式为y=x,∴∠CnOAn=30°.
∵r1=,∴OC1=2r1=,
∵ OC2=2r2,∴++r2=2r2,
解得:r2=1.同理:可求出r3=3,r4=9,…rn=3n 2.
故答案为:rn=3n 2.
三.解答题
17.证明:连结OC、OD,如图,
∵AB是⊙O的直径,M,N分别是AO,BO的中点,∴OM=ON,
∵CM⊥AB,DN⊥AB,∴∠OMC=∠OND=90°,
在Rt△OMC和Rt△OND中,
,
∴Rt△OMC≌Rt△OND(HL),∴∠COM=∠DON,
∴ = .
18.点P为半圆AB的中点.理由如下:
连接OP,如图,
∵∠OCD的平分线交圆于点P,∴∠PCD=∠PCO,
∵OC=OP,∴∠PCO=∠OPC,
∴∠PCD=∠OPC,∴OP∥CD,
∵CD⊥AB,∴OP⊥AB,∴弧PA=弧PB,
即点P为半圆的中点.
19.(1)设⊙O的半径为r,
∵∠ABC=90°∴弧EFG所对的圆心角的度数为180°,
∴=(1+)π,即r=1+;
(2)答:圆心O在直线BF上.
理由如下:
∵DE∥BF,∴∠ADE=∠AFB.
∵四边形DEBF是⊙O的内接四边形,∴∠AFB+∠DEB=180°.
∵∠AED+∠DEB=180°,∴∠AFB=∠AED,∴∠ADE=∠AED,∴AD=AE=a.
∵DF=2+﹣a,∴AF=AD+DF=2+.
在Rt△ABC中,∠ABC=90°且F为AC中点,∴BF=AF=2+.
∵r=1+ ,∴BF=2r.
∵B、F都在⊙O上,∴BF为⊙O直径,
∴点O在直线BF上.
20.解:
作法:连结PO,分别以P、O为圆心,大于PO的长度为半径画弧,交于两点,连结两点交PO于点A;以点A为圆心,PA长为半径画弧,交于点Q,连结PQ,PQ即为所求.
作法:连结PO,分别以P、O为圆心,以大于PO的长度为半径画弧交PO上方于点B,连结BP、BO;以点B为圆心,任意长为半径画弧交BP、BO于C、D两点,分别以于C、D两点为圆心,大于CD的长度为半径画弧交于一点,连结该点与B点,并将其反向延长交PQ于点A,以点A为圆心,PA长为半径画弧,交于点Q,连结PQ,PQ即为所求.
21.(1)如图1,连接BI,
∵I是△ABC的内心,∴∠1=∠2,∠3=∠4,
∵∠BIE=∠1+∠3,∠IBE=∠5+∠4,而∠5=∠1=∠2,
∴∠BIE=∠IBE,∴IE=BE.
(2)四边形BECI是菱形,
如图2,∵∠BED=∠CED=60°,
∴∠ABC=∠ACB=60°,∴BE=CE,
∵I是△ABC的内心,∴∠4=∠ABC=30°,∠ICD=∠30°,∴∠4=∠ICD,
∴BI=IC,
由(1)证得IE=BE,∴BE=CE=BI=IC,
∴四边形BECI是菱形.
22.(1)∵△ABC中,AB=AC,∠BAC=120°, ∴∠B=∠C=30°,
∵OA=OB,∴∠BAO=∠B=30°,∴∠AOC=30°+30°=60°,∴∠OAC=90°,
∵OA=5,∴OC=2AO=10.
(2)连接OD,
∵∠AOC=60°,AD∥BC,∴∠DAO=∠AOC=60°,
∵OD=OA,∴∠ADO=60°,∴∠DOB=∠ADO=60°,
∵OD=OB,∴△DOB是等边三角形,
∴BD=OB=OA,
在Rt△OAC中,OC=2BD,由勾股定理得:AC=BD,
∴=.
23.(1)当交BC于点M时,此时半径r最小,
设,如图1所示,
在和中,由勾股定理可知:
∴,解得:
∴,半径
(2)如图2所示,连接OM,过点A作交BC于点D,过点O作交AD于点F;
由(1)知,,,;
∴,;
∴在中,,即
整理得:;
∵点M在线段BC上∴
∴
(3)如图3所示:
一.选择题(每小题2分,共12分)
1.如图,CD是的直径,弦AB⊥CD于点G,直线EF与相切与点D,则下列结论中不一定正确的是( )
A. AG=BG B. AB∥EF C. AD∥BC D. ∠ABC=∠ADC
2.如图,是⊙的直径,是⊙上两点,若,则的度数是( )
A. B. C. D.
3.如图,已知⊙O的半径为5,弦AB、CD所对的圆心角分别是∠AOB、∠COD,若∠AOB与∠COD互补,弦CD=6,则点O到弦AB的距离为( )
A.6 B.8 C.3 D.4
4.如图,在 O中,,BC=6.AC=3,I是△ABC的内心,则线段OI的值为( )
A.1 B.3 C.5 D.
5.如图,的圆心的坐标为,半径为1,直线的表达式为,是直线上的动点,是上的动点,则的最小值是( )
A. B. C. D.
6.如图,四边形ABCD内接于⊙O,AB=CB,∠BAC=30°,BD=,则AD+CD的值为( )
A.3 B.2 C.1 D.不能确定
二.填空题(每小题2分,共20分)
7.过圆内一点的最长的弦、最短弦的长度分别是8cm,6cm,则___.
8.如图所示,外接圆的圆心坐标是________.
9.如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为___度.
10.在直角坐标系中,☉M的圆心坐标是(m,0),半径是2,如果☉M与y轴相切,那么m=________;如果☉M与y轴相交,那么m的取值范围是________.
11.如图,在△ABC中,∠ACB=90°,∠A=30°,AB=4,以点B为圆心,BC长为半径画弧,交边AB于点D,则CD的长为______.
12.如图,将半径为的圆形纸板,沿着三边分别长、、的的外侧无滑动地滚动一周并回到开始的位置,则圆心所经过的路线长度是______.
13.如图,在正五边形ABCDE中,AC为对角线,以点A为圆心,AE为半径画圆弧交AC于点F,连结EF,则∠1的度数为__.
14.如图所示,经过B(2,0)、C(6,0)两点的⊙H与y轴的负半轴相切于点A,双曲线y= 经过圆心H,则反比例函数的解析式为________.
15.如图,在△ABC中,AB=5,AC=4,BC=3,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是________.
16.如图,n个半圆弧依次相外切,他们的圆心都在x轴的正半轴上,并都与直线y=x相切,设半圆C1、半圆C2、半圆C3…、半圆Cn的半径分别为r1、r2、r3…、rn,当r1=时,rn=__________.(n>1的自然数)
三.解答题(共68分)
17.(8分)如图,已知AB是⊙O的直径,M,N分别是AO,BO的中点,CM⊥AB,DN⊥AB.求证: .
18.(8分)如图,已知AB为⊙O的直径,点C为半圆ACB上的动点(不与A、B两点重合),过点C作弦CD⊥AB,∠OCD的平分线交圆于点P,则点P的位置有何规律?请证明你的结论.
19.(10分)如图,在Rt△ABC中,∠ABC=90°,点F为AC中点,⊙O经过点B,F,且与AC交于点D,与AB交于点E,与BC交于点G,连结BF,DE,弧EFG的长度为(1+)π.
(1)求⊙O的半径;
(2)若DE∥BF,且AE=a,DF=2+﹣a,请判断圆心O和直线BF的位置关系,并说明理由.
20.(10分)如图,已知P是外一点.用两种不同的方法过点P作的一条切线.要求:
(1)用直尺和圆规作图;
(2)保留作图的痕迹,写出必要的文字说明.
21.(10分)如图,I是△ABC的内心,AI的延长线交边BC于点D,交△ABC的外接圆于点E.
(1)BE与IE相等吗?请说明理由.
(2)连接BI,CI,CE,若∠BED=∠CED=60°,猜想四边形BECI是何种特殊四边形,并证明你的猜想.
22.(10分)已知△ABC中,AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心、OB为半径作圆,且⊙O过A点.
(1)如图①,若⊙O的半径为5,求线段OC的长;
(2)如图②,过点A作AD∥BC交⊙O于点D,连接BD,求的值.
23.(12分)如图1,中,,半径为r的经过点A且与相切,切点M在线段上(包含点M与点B、C重合的情况).
(1)半径r的最小值等于________:
(2)设,求半径r关于x的函数表达式;
(3)当时,请在图2中作出点M及满足条件的.
(要求:尺规作图,不写作法,保留作图痕迹,并用2B铅笔或黑色水笔加黑加粗)
答案
一.选择题
1.C
【解析】解:(A)∵CD是的直径,弦AB⊥CD于点G,∴由垂径定理可知:AG=BG.结论正确.
(B)∵直线EF与相切与点D,∴EF⊥AD.∴AB∥EF.结论正确.
(C)要AD∥BC,即要∠ABC=∠BAD,由圆周角定理,∠ABC=∠ADC,即要∠BAD =∠ADC,即要AG=DG,但没此条件.结论错误.
(D)∵∠ABC和∠ADC是同弧所对的圆周角,∴∠ABC=∠ADC.结论正确.
故选:C.
2.C
【解析】解:连接AC、AD,∴∠ADC=∠ABC=40°
∵是⊙的直径∴∠ADB=90°,∴∠BDC=∠ADB-∠ADC=90°-40°=50°.
故选C.
3.C
【解析】延长CO交⊙O于E,连接DE,过O作OF⊥DE于F,OH⊥CD于H,OG⊥AB于G,线段OG的长是点O到弦AB的距离,
∵∠COD和∠DOE互补,∠COD和∠AOB互补,∴∠DOE=∠AOB,
∴DE=AB,OF=OG,
∵OH⊥DC,CD=6,OH过O,∴DH=HCDC=3,∠OHD=∠OHC=90°,
由勾股定理得:OH4,
∵OC=OE,DH=HC,OH=4,∴DE=2OH=8,
∵OF⊥DE,OF过O,∴DF=EF=DE=4,
在Rt△DFO中,由勾股定理得:OF3,∴OG=OF=3,
即点O到AB的距离是3,
故选C.
4.C
【解析】如图,连接AO,延长AO交BC于H,连接OB.
∵,∴AB=AC,AH⊥BC,∴BH=CH=3,
∴AH9,
设OA=OB=x,
在Rt△BOH中,∵OB2=OH2+BH2,
∴x2=(9﹣x)2+32,∴x=5,∴OH=AHAO=9﹣5=4,
∵S△ABC BC AH (AB+AC+BC) IH,∴IH1,∴OI=OH﹣IH=4﹣(1)=5-,
故选C.
5.A
【解析】解:过点作直线,交圆于点,此时的值最小,连接、,作于,于,
∵,∴,,∴,,∴,
∵四边形是正方形,∴,∴,,
设,,则,
∵,,
∴,,
解得:,
∵的半径为1,∴,
故选:A.
6.A
【解析】如图,过点B作BE⊥AD于E,BF⊥DC交DC的延长线于F.
∵AB=BC,∴,∴∠BDE=∠BDF,
∵∠DEB=∠DFB=90°,DB=DB,
∴△BDE≌△BDF(AAS),∴BE=BF,DE=DF,
∵∠AEB=∠F=90°,BA=BC,BE=BF,∴Rt△BEA≌Rt△BFC(HL),∴AE=CF,
∴AD+DC=DE+AE+DF﹣CF=2DF,
∵∠BDF=∠BAC=30°,BD,∴BFBD,
∴DF,∴DA+DC=3,
故选A.
二.填空题
7.
【解析】如图所示,直径AB⊥弦CD于点P,根据题意,得AB=8cm,CD=6cm,OC=AB=4cm,
∵CD⊥AB,∴CP=CD=3cm.根据勾股定理,得OP=(cm),
8.
【解析】解:作AB和BC的垂直平分线,它们的交点P为△ABC外接圆圆心,
∵ P点坐标是P(5,2),∴ 外接圆的圆心坐标是(5,2).
故答案为(5,2).
9.65
【解析】解:∵∠CBE=50°,∴∠ABC=180°﹣∠CBE=180°﹣50°=130°.∵四边形ABCD为⊙O的内接四边形,∴∠D=180°﹣∠ABC=180°﹣130°=50°.∵DA=DC,∴∠DAC==65°.故答案为65.
10.±2 -2
∵☉M与y轴相切,∴圆心到y轴的距离等于该圆的半径,,故m=±2,
∵☉M与y轴相交,∴圆心到y轴的距离小于等于2,即圆心到y轴的距离|m|<2,∴-2
【解析】解:连接CD,
∵∠ACB=90°,∠A=30°,AB=4,∴∠B=60°,BC=AB=2,
∵以点B为圆心,BC长为半径画弧,交边AB于点D,
∴△BCD是等边三角形,∴CD=BC=2,
故答案为2.
12.
【解析】圆在三角形的三个角的顶点处旋转的角度是:360°,
则旋转的路线长是:l==,
圆心O所经过的路线的长度=6+5+4+=15+.
故答案为:15+.
13.54°
【解析】解:∵五边形ABCDE是正五边形,∴∠EAB=∠ABC==108°,
∵BA=BC,∴∠BAC=∠BCA==36°,∴∠EAF=108°﹣36°=72°,
∵以点A为圆心,AE为半径画圆弧交AC于点F,∴AE=AF,∴∠1==54°.
故答案为:54°.
14.y=﹣
【解析】过H作HE⊥BC于点E,连接BH,AH,如图,
∵B(2,0),C(6,0),∴BC=4,∴BE=BC=2,∴OE=OB+BE=2+2=4,
又 ⊙H与y轴切于点A,∴AH⊥y轴,∴AH=OE=4,∴BH=4,
在Rt△BEH中,BE=2,BH=4,∴HE==2,∴H点坐标为(4,-2),
∵y=经过圆心H,∴k=-8,
∴反比例函数的解析式为y=﹣,
故答案为y=﹣.
15.4.5
【解析】如图,设⊙O与AC相切于点E,连接OE,作OP1⊥BC垂足为P1交⊙O于Q1,此时垂线段OP1最短,P1Q1最小值为OP1﹣OQ1 ,
∵AB=5,AC=4,BC=3,∴AB2=AC2+BC2 , ∴∠C=90°,
∵∠OP1B=90°,∴OP1∥AC
∵AO=OB,∴P1C=P1B,∴OP1= AC=2,
∴P1Q1最小值为OP1﹣OQ1=0.5,
如图,当Q2在AB边上时,P2与B重合时,P2Q2经过圆心,经过圆心的弦最长,
P2Q2最大值=2.5+1.5=4,
∴PQ长的最大值与最小值的和是4.5.
故答案为4.5.
16.3n 2
【解析】解:过点Cn作CnAn⊥直线于点An,如图所示,
∵直线解析式为y=x,∴∠CnOAn=30°.
∵r1=,∴OC1=2r1=,
∵ OC2=2r2,∴++r2=2r2,
解得:r2=1.同理:可求出r3=3,r4=9,…rn=3n 2.
故答案为:rn=3n 2.
三.解答题
17.证明:连结OC、OD,如图,
∵AB是⊙O的直径,M,N分别是AO,BO的中点,∴OM=ON,
∵CM⊥AB,DN⊥AB,∴∠OMC=∠OND=90°,
在Rt△OMC和Rt△OND中,
,
∴Rt△OMC≌Rt△OND(HL),∴∠COM=∠DON,
∴ = .
18.点P为半圆AB的中点.理由如下:
连接OP,如图,
∵∠OCD的平分线交圆于点P,∴∠PCD=∠PCO,
∵OC=OP,∴∠PCO=∠OPC,
∴∠PCD=∠OPC,∴OP∥CD,
∵CD⊥AB,∴OP⊥AB,∴弧PA=弧PB,
即点P为半圆的中点.
19.(1)设⊙O的半径为r,
∵∠ABC=90°∴弧EFG所对的圆心角的度数为180°,
∴=(1+)π,即r=1+;
(2)答:圆心O在直线BF上.
理由如下:
∵DE∥BF,∴∠ADE=∠AFB.
∵四边形DEBF是⊙O的内接四边形,∴∠AFB+∠DEB=180°.
∵∠AED+∠DEB=180°,∴∠AFB=∠AED,∴∠ADE=∠AED,∴AD=AE=a.
∵DF=2+﹣a,∴AF=AD+DF=2+.
在Rt△ABC中,∠ABC=90°且F为AC中点,∴BF=AF=2+.
∵r=1+ ,∴BF=2r.
∵B、F都在⊙O上,∴BF为⊙O直径,
∴点O在直线BF上.
20.解:
作法:连结PO,分别以P、O为圆心,大于PO的长度为半径画弧,交于两点,连结两点交PO于点A;以点A为圆心,PA长为半径画弧,交于点Q,连结PQ,PQ即为所求.
作法:连结PO,分别以P、O为圆心,以大于PO的长度为半径画弧交PO上方于点B,连结BP、BO;以点B为圆心,任意长为半径画弧交BP、BO于C、D两点,分别以于C、D两点为圆心,大于CD的长度为半径画弧交于一点,连结该点与B点,并将其反向延长交PQ于点A,以点A为圆心,PA长为半径画弧,交于点Q,连结PQ,PQ即为所求.
21.(1)如图1,连接BI,
∵I是△ABC的内心,∴∠1=∠2,∠3=∠4,
∵∠BIE=∠1+∠3,∠IBE=∠5+∠4,而∠5=∠1=∠2,
∴∠BIE=∠IBE,∴IE=BE.
(2)四边形BECI是菱形,
如图2,∵∠BED=∠CED=60°,
∴∠ABC=∠ACB=60°,∴BE=CE,
∵I是△ABC的内心,∴∠4=∠ABC=30°,∠ICD=∠30°,∴∠4=∠ICD,
∴BI=IC,
由(1)证得IE=BE,∴BE=CE=BI=IC,
∴四边形BECI是菱形.
22.(1)∵△ABC中,AB=AC,∠BAC=120°, ∴∠B=∠C=30°,
∵OA=OB,∴∠BAO=∠B=30°,∴∠AOC=30°+30°=60°,∴∠OAC=90°,
∵OA=5,∴OC=2AO=10.
(2)连接OD,
∵∠AOC=60°,AD∥BC,∴∠DAO=∠AOC=60°,
∵OD=OA,∴∠ADO=60°,∴∠DOB=∠ADO=60°,
∵OD=OB,∴△DOB是等边三角形,
∴BD=OB=OA,
在Rt△OAC中,OC=2BD,由勾股定理得:AC=BD,
∴=.
23.(1)当交BC于点M时,此时半径r最小,
设,如图1所示,
在和中,由勾股定理可知:
∴,解得:
∴,半径
(2)如图2所示,连接OM,过点A作交BC于点D,过点O作交AD于点F;
由(1)知,,,;
∴,;
∴在中,,即
整理得:;
∵点M在线段BC上∴
∴
(3)如图3所示:
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
