苏科版九年级数学上册试题 第4章 等可能条件下的概率 章节检测卷 (含详解)
文档属性
| 名称 | 苏科版九年级数学上册试题 第4章 等可能条件下的概率 章节检测卷 (含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 814.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-24 21:29:52 | ||
图片预览




文档简介
第4章《等可能条件下的概率》章节检测卷
一.选择题(每小题2分,共12分)
1.下列说法正确的是( )
A.“明天的降水概率为 80%”,意味着明天有 80%的时间降雨
B.掷一枚质地均匀的骰子,“点数为奇数”与“点数为偶数”的可能性相等
C.“某彩票中奖概率是 1%”,表示买 100 张这种彩票一定会中奖
D.小明上次的体育测试成绩是“优秀”,这次测试成绩一定也是“优秀”
2.将一枚飞镖任意投掷到如图所示的正六边形镖盘上,飞镖落在白色区域的概率为( )
A. B. C. D.无法确定
3.如图,随机闭合开关,,中的两个,则能让两盏灯泡同时发光的概率为( )
A. B. C. D.
4.甲、乙、丙三人进行乒乓球比赛,规则是:两人比赛,另一人当裁判,输者将在下一局中担任裁判,每一局比赛没有平局.已知甲、乙各比赛了4局,丙当了3次裁判.问第2局的输者是( )
A.甲 B.乙 C.丙 D.不能确定
5.一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都随机选择一条路径,并且选择每条路径的可能性相等,则它获得食物的概率是( )
A. B. C. D.
6.如图,在3×3的正方形网格中,点A、B在格点(网格线的交点)上,在其余14个格点上任取一个点C,使△ABC成为轴对称图形的概率是( )
A. B. C. D.
二.填空题(每小题2分,共20分)
7.某鱼塘里养了1600条鲤鱼、若干条草鱼和800条罗非鱼,该鱼塘主通过多次捕捞试验后发现,捕捞到草鱼的频率稳定在0.5左右,若该鱼塘主随机在鱼塘捕捞一条鱼,则捞到鲤鱼的概率约为_________.
8.小红和小明在操场上做游戏,他们先在地上画了半径为2m和3m的同心圆,如图,然后蒙上眼睛在一定距离外向圈内掷小石子,掷中阴影部分小红胜,否则小明胜,未掷入圈内不算,获胜可能性大的是_______。
9.如图,A是正方体小木块(质地均匀)的一顶点,将木块随机投掷在水平桌面上,则A与桌面接触的概率是_______.
10.某十字路口汽车能够行驶的方向有左转、右转还有直行.假设所有的汽车经过这个十字路口时,所行驶的这三种方向可能性大小相同,则两辆汽车经过这个十字路口时,在这三种方向中,它们行驶的方向相同的概率为________.
11.小明和小亮做游戏,先是各自背着对方在纸上写一个自然数,然后同时呈现出来.他们约定:若两人所写的数都是奇数或都是偶数,则小明获胜;否则,小亮获胜.这个游戏对双方_____.(填“公平”或“不公平”).
12.七巧板是一种古老的中国传统智力玩具.如图,在正方形纸板ABCD中,BD为对角线,E,F分别为BC,CD的中点,AP⊥EF分别交BD,EF于O,P两点,M,N分别为BO,DO的中点,连接MP,NF,沿图中实线剪开即可得到一副七巧板.在剪开之前,随机向正方形ABCD内投一粒米,则米粒落在四边形BMPE内的概率为___.
13.用100万元资金投资一项技术改造项目,如果成功,则可盈利400万元;如果失败,将亏损全部投资.已知成功的概率是,这次投资项目期望大致可盈利________万元.
14.一只不透明的布袋中有三种小球(除颜色以外没有任何区别),分别是2个红球,3个白球和5个黑球,搅匀之后,每次摸出一只小球不放回.在连续2次摸出的都是黑球的情况下,第3次摸出黑球的概率是________.
15.“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形.有一“赵爽弦图”飞镖板,其直角三角形的两条直角边的长分别是2和4.小明同学距飞镖板一定距离向飞镖板投掷飞镖(假设投掷的飞镖均扎在飞镖板上),则投掷一次飞镖扎在中间小正形区域(含边)的概率是_____.
16.义乌国际小商品博览会某志愿小组有五名翻译,其中一名只会翻译阿拉伯语,三名只会翻译英语,还有一名两种语言都会翻译.若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是
三.解答题(共68分)
17.(8分)下列成语,哪些刻画的是必然事件?哪些刻画的是不可能事件?哪些刻画的是随机事件?
(1)万无一失;(2)胜败乃兵家常事;(3)水中捞月;
(4)十拿九稳;(5)海枯石烂;(6)守株待兔;(7)百战百胜;(8)九死一生.
你还能举出类似的成语吗?
18.(10分)如图所示是一块三角形纸板,其中,,,一只蚂蚁在这张纸上爬行,求蚂蚁踩到阴影部分的概率.
19.(10分)有5张不透明的卡片,除正面上的图案不同外,其他均相同.将这5张卡片背面向上洗匀后放在桌面上.
(1)从中随机抽取1张卡片,卡片上的图案是中心对称图形的概率为_____.
(2)若从中随机抽取1张卡片后不放回,再随机抽取1张,请用画树状图或列表的方法,求两次所抽取的卡片恰好都是轴对称图形的概率.
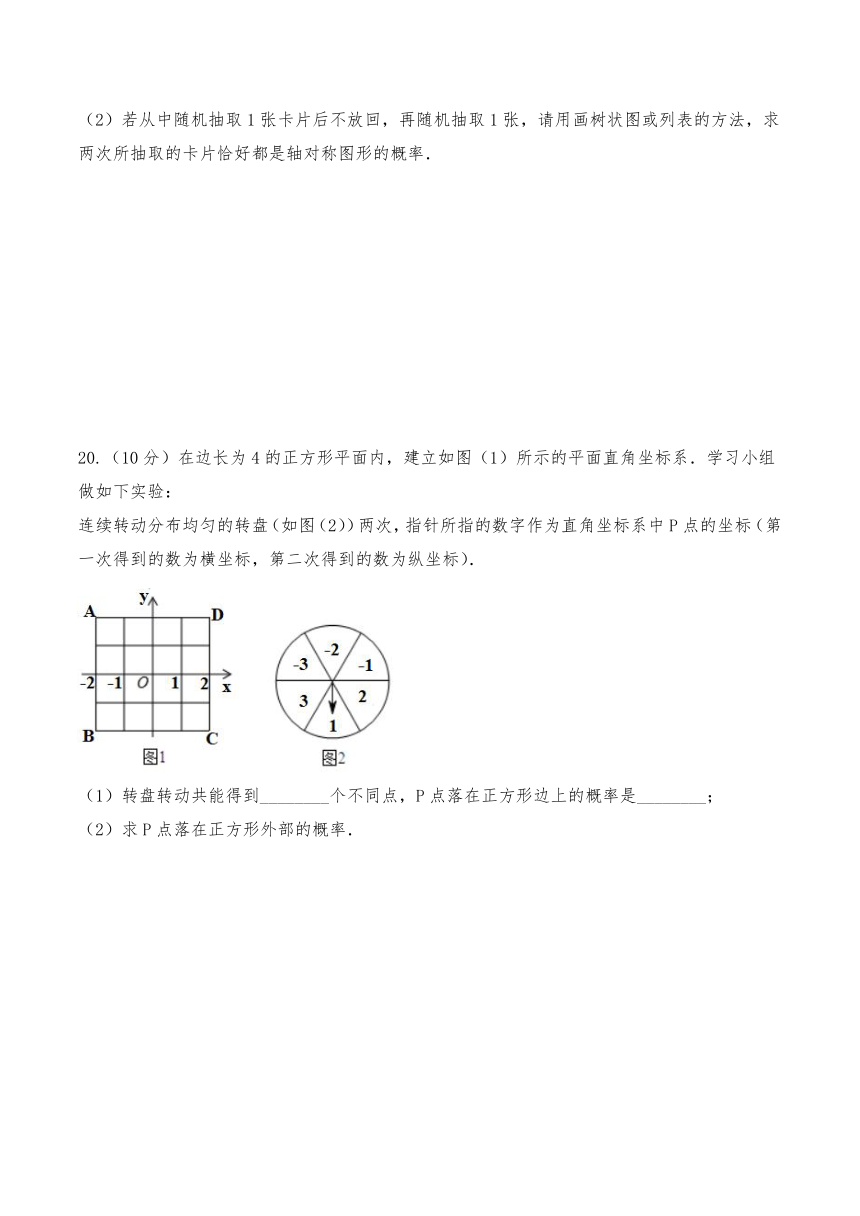
20.(10分)在边长为4的正方形平面内,建立如图(1)所示的平面直角坐标系.学习小组做如下实验:
连续转动分布均匀的转盘(如图(2))两次,指针所指的数字作为直角坐标系中P点的坐标(第一次得到的数为横坐标,第二次得到的数为纵坐标).
(1)转盘转动共能得到________个不同点,P点落在正方形边上的概率是________;
(2)求P点落在正方形外部的概率.
21.(10分)动物学家通过大量的调查估计出,某种动物活到20岁的概率为0.8,活到25岁的概率是0.5,活到30岁的概率是0.3.现年20岁的这种动物活到25岁的概率为多少?现年25岁的这种动物活到30岁的概率为多少?
22.(10分)游戏者同时转动如图的两个转盘进行“配紫色游戏”,若要使游戏者获胜的概率为,转盘B不动,转盘A应该如何设计?并写出解答过程说明理由.
23.(10分)如图所示,在方格纸中,△ABC的三个顶点及D,E,F,G,H五个点分别位于小正方形的顶点上.
(1)现以D,E,F,G,H中的三个点为顶点画三角形,在所画的三角形中与△ABC不全等但面积相等的三角形是 (只需要填一个三角形);
(2)先从D,E两个点中任意取一个点,再从F,G,H三个点中任意取两个不同的点,以所取的这三个点为顶点画三角形,画树状图求所画三角形与△ABC面积相等的概率.
答案
一.选择题
1.B
【解析】
A.“明天的降水概率为80%”,只能说明有很大机会下雨,而不能说明有80%的时间降雨,故A错误;
C.“某彩票中奖概率是1%”,只能说明中奖的机会很小,故C错误;
D.小明上次的体育测试成绩与这次测试成绩并没有任何关系,故D错误.
故答案选:B.
2.B
【解析】
如图,根据正六方形的性质可得,△AOC △ABC(SSS),同理△EOC △EDC, △AFE △AOE,
所以,阴影面积=空白部分面积
所以,飞镖落在白色区域的概率为
故选B
3.C
【解析】根据题意画出树状图如下:
共有6种等可能的结果,能让两盏灯泡同时发光的有2种情况,
∴,故选C.
4.C
【解析】由题意知道,甲和乙各与丙比赛了一场.丙当了三次裁判,说明甲和乙比赛了三场,这三场中间分别是甲和丙,乙和丙比赛.因此第一,三,五场比赛是甲和乙比赛,第二,四场是甲和丙,乙和丙比赛,并且丙都输了.故第二局输者是丙.
解:由题意,知:三场比赛的对阵情况为:
第一场:甲VS乙,丙当裁判;
第二场:乙VS丙,甲当裁判;
第三场:甲VS乙,丙当裁判;
第四场:甲VS丙,乙当裁判;
第五场:乙VS甲,丙当裁判;
由于输球的人下局当裁判,因此第二场输的人是丙.
故选C.
5.A
【解析】解:∵一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都会随机的选择一条路径,
∴它有6种路径,
∵获得食物的有2种路径,
∴获得食物的概率是:
故选A.
6.C
【解析】C点落在如图所示网格中的4个格点时,△ABC为等腰三角形,所以在其余14个格点上任取一个点C,使△ABC成为轴对称图形的概率==.
故选C.
二.填空题
7.
【解析】解:∵捕捞到草鱼的频率稳定在0.5左右,
设草鱼的条数为x,可得:
;
解得:x=2400,
经检验:x=2400是原方程的解且符合实际意义
∴由题意可得,捞到鲤鱼的概率为
,
故答案为:.
8.小红
【解析】∵大圆的半径为3m,小圆半径为2m,
∴S大圆=m2,小圆面积=m2,
∴S阴影=(m2),
∴小红获胜的概率为:,而小明获胜的概率=,
∵,
∴小红获胜的可能性大.
故答案为:小红.
9.
【解析】∵正方体的面共有6个,与A相邻的面有3个,
∴A与桌面接触的概率是.
10.
【解析】用树状图列举两辆汽车行驶的方向所有可能的结果,如图所示.
由树状图可知,这两辆汽车行驶的方向共有9种等可能出现的结果,其中它们行驶的方向相同的有3种结果,所以它们行驶的方向相同的概率为.
故答案为:.
11.公平
【解析】根据题意画出树状图如下:
由图可知:共有四种等可能结果出现,其中小明获胜的有两种,小亮获胜的也有两种,
∴P(小明获胜)=,P(小亮获胜)=,
∴P(小明获胜)=P(小亮获胜),
∴该游戏是“公平”的.
故答案为公平.
12..
【解析】设BE=a,
∵E,F分别为BC,CD的中点,∴EF∥BD,EF=BD,BC=2a,∴BD=2a,
∵AP⊥EF,∴AP⊥BD,∴BO=OD,∴点P在AC上,∴PE=EF,∴PE=BM,
∴四边形BMPE是平行四边形,∴BO=BD,
∵M为BO的中点,∴BM=BD,
∵E为BC的中点,∴BC=2a,,
过M作MH⊥BC于H,
∴,∴S正方形ABCD=4a2,S四边形BMPE=a2,
∴米粒落在四边形BMPE内的概率为,
故答案为.
13.200
【解析】.
故这次投资项目期望大致可以盈利200万元.
14.
【解析】袋中有2个红球,3个白球和5个黑球,共10球,
则每次摸出一只小球不放回,在连续2次摸出的都是黑球的情况下,第3次摸出黑球的概率是:.
故答案为.
15.
【解析】
解:大正方形的边长为:,
总面积为20,
∵阴影区域的边长为2,
∴面积为2×2=4;
故飞镖落在阴影区域的概率为,
故答案为
16.
【解析】将一名只会翻译阿拉伯语用A表示,三名只会翻译英语都用B表示,一名两种语言都会翻译用C表示,画树状图得:
∵共有20种等可能的结果,该组能够翻译上述两种语言的有14种情况,
∴该组能够翻译上述两种语言的概率为:.
故答案为:
三.解答题
17.(1)万无一失必然事件;(2)胜败乃兵家常事是随机事件;
(3)水中捞月不可能事件;(4)十拿九稳随机事件;(5)海枯石烂不可能事件;
(6)守株待兔随机事件;(7)百战百胜是必然事件;(8)九死一生随机事件.
18.解:连接AE,BF,CD.
,,,
利用三角形中线的性质可得,
被分为7个面积相同的三角形,中间阴影部分的三角形的面积是的,
所以蚂蚁踩到阴影部分的概率是.
19.解:(1)中心对称图形的卡片是A和D,所以从中随机抽取1张卡片,卡片上的图案是中心对称图形的概率为,故答案为;
(2)轴对称图形的卡片是B、C、E.
画树状图如下:
由树状图知,共有20种等可能结果,其中两次所抽取的卡片恰好都是轴对称图形的有6种结果,分别是(B,C)、(B,E)、(C,B)、(C,E)、(E,B)、(E,C),
∴两次所抽取的卡片恰好都是轴对称图形的概率=.
20.解:(1)列表如下:
1 2 3
1
2
3
转盘转动共能得到36个不同点,P点落在正方形边上的有12个,则P点落在正方形边上的概率是.
故答案为36, .
(2)根据图表可得,转盘转动共能得到36个不同点,其中落在正方形外部的有20个,则P点落在正方形外部的概率是.
21.现年20岁的这种动物活到25岁的概率为=0.625,
现年25岁的这种动物活到30岁的概率为=0.6,
答:现年20岁的这种动物活到25岁的概率为0.625,现年25岁的这种动物活到30岁的概率为0.6.
22.将转盘A平均分成10分,一份是蓝色,一份是红色,其他是绿色.
则共有20种,能配成紫色的情况有两种,
∴P(配成紫色)=
23.(1)、的面积为:,
只有△DFG或△DHF的面积也为6且不与△ABC全等,
与△ABC不全等但面积相等的三角形是:△DFG或△DHF;
(2)、画树状图如图所示:
由树状图可知共有6种等可能结果, 其中与△ABC面积相等的有3种,即△DHF,△DGF,△EGF,
所以所画三角形与△ABC面积相等的概率P=
答:所画三角形与△ABC面积相等的概率为.
一.选择题(每小题2分,共12分)
1.下列说法正确的是( )
A.“明天的降水概率为 80%”,意味着明天有 80%的时间降雨
B.掷一枚质地均匀的骰子,“点数为奇数”与“点数为偶数”的可能性相等
C.“某彩票中奖概率是 1%”,表示买 100 张这种彩票一定会中奖
D.小明上次的体育测试成绩是“优秀”,这次测试成绩一定也是“优秀”
2.将一枚飞镖任意投掷到如图所示的正六边形镖盘上,飞镖落在白色区域的概率为( )
A. B. C. D.无法确定
3.如图,随机闭合开关,,中的两个,则能让两盏灯泡同时发光的概率为( )
A. B. C. D.
4.甲、乙、丙三人进行乒乓球比赛,规则是:两人比赛,另一人当裁判,输者将在下一局中担任裁判,每一局比赛没有平局.已知甲、乙各比赛了4局,丙当了3次裁判.问第2局的输者是( )
A.甲 B.乙 C.丙 D.不能确定
5.一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都随机选择一条路径,并且选择每条路径的可能性相等,则它获得食物的概率是( )
A. B. C. D.
6.如图,在3×3的正方形网格中,点A、B在格点(网格线的交点)上,在其余14个格点上任取一个点C,使△ABC成为轴对称图形的概率是( )
A. B. C. D.
二.填空题(每小题2分,共20分)
7.某鱼塘里养了1600条鲤鱼、若干条草鱼和800条罗非鱼,该鱼塘主通过多次捕捞试验后发现,捕捞到草鱼的频率稳定在0.5左右,若该鱼塘主随机在鱼塘捕捞一条鱼,则捞到鲤鱼的概率约为_________.
8.小红和小明在操场上做游戏,他们先在地上画了半径为2m和3m的同心圆,如图,然后蒙上眼睛在一定距离外向圈内掷小石子,掷中阴影部分小红胜,否则小明胜,未掷入圈内不算,获胜可能性大的是_______。
9.如图,A是正方体小木块(质地均匀)的一顶点,将木块随机投掷在水平桌面上,则A与桌面接触的概率是_______.
10.某十字路口汽车能够行驶的方向有左转、右转还有直行.假设所有的汽车经过这个十字路口时,所行驶的这三种方向可能性大小相同,则两辆汽车经过这个十字路口时,在这三种方向中,它们行驶的方向相同的概率为________.
11.小明和小亮做游戏,先是各自背着对方在纸上写一个自然数,然后同时呈现出来.他们约定:若两人所写的数都是奇数或都是偶数,则小明获胜;否则,小亮获胜.这个游戏对双方_____.(填“公平”或“不公平”).
12.七巧板是一种古老的中国传统智力玩具.如图,在正方形纸板ABCD中,BD为对角线,E,F分别为BC,CD的中点,AP⊥EF分别交BD,EF于O,P两点,M,N分别为BO,DO的中点,连接MP,NF,沿图中实线剪开即可得到一副七巧板.在剪开之前,随机向正方形ABCD内投一粒米,则米粒落在四边形BMPE内的概率为___.
13.用100万元资金投资一项技术改造项目,如果成功,则可盈利400万元;如果失败,将亏损全部投资.已知成功的概率是,这次投资项目期望大致可盈利________万元.
14.一只不透明的布袋中有三种小球(除颜色以外没有任何区别),分别是2个红球,3个白球和5个黑球,搅匀之后,每次摸出一只小球不放回.在连续2次摸出的都是黑球的情况下,第3次摸出黑球的概率是________.
15.“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形.有一“赵爽弦图”飞镖板,其直角三角形的两条直角边的长分别是2和4.小明同学距飞镖板一定距离向飞镖板投掷飞镖(假设投掷的飞镖均扎在飞镖板上),则投掷一次飞镖扎在中间小正形区域(含边)的概率是_____.
16.义乌国际小商品博览会某志愿小组有五名翻译,其中一名只会翻译阿拉伯语,三名只会翻译英语,还有一名两种语言都会翻译.若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是
三.解答题(共68分)
17.(8分)下列成语,哪些刻画的是必然事件?哪些刻画的是不可能事件?哪些刻画的是随机事件?
(1)万无一失;(2)胜败乃兵家常事;(3)水中捞月;
(4)十拿九稳;(5)海枯石烂;(6)守株待兔;(7)百战百胜;(8)九死一生.
你还能举出类似的成语吗?
18.(10分)如图所示是一块三角形纸板,其中,,,一只蚂蚁在这张纸上爬行,求蚂蚁踩到阴影部分的概率.
19.(10分)有5张不透明的卡片,除正面上的图案不同外,其他均相同.将这5张卡片背面向上洗匀后放在桌面上.
(1)从中随机抽取1张卡片,卡片上的图案是中心对称图形的概率为_____.
(2)若从中随机抽取1张卡片后不放回,再随机抽取1张,请用画树状图或列表的方法,求两次所抽取的卡片恰好都是轴对称图形的概率.
20.(10分)在边长为4的正方形平面内,建立如图(1)所示的平面直角坐标系.学习小组做如下实验:
连续转动分布均匀的转盘(如图(2))两次,指针所指的数字作为直角坐标系中P点的坐标(第一次得到的数为横坐标,第二次得到的数为纵坐标).
(1)转盘转动共能得到________个不同点,P点落在正方形边上的概率是________;
(2)求P点落在正方形外部的概率.
21.(10分)动物学家通过大量的调查估计出,某种动物活到20岁的概率为0.8,活到25岁的概率是0.5,活到30岁的概率是0.3.现年20岁的这种动物活到25岁的概率为多少?现年25岁的这种动物活到30岁的概率为多少?
22.(10分)游戏者同时转动如图的两个转盘进行“配紫色游戏”,若要使游戏者获胜的概率为,转盘B不动,转盘A应该如何设计?并写出解答过程说明理由.
23.(10分)如图所示,在方格纸中,△ABC的三个顶点及D,E,F,G,H五个点分别位于小正方形的顶点上.
(1)现以D,E,F,G,H中的三个点为顶点画三角形,在所画的三角形中与△ABC不全等但面积相等的三角形是 (只需要填一个三角形);
(2)先从D,E两个点中任意取一个点,再从F,G,H三个点中任意取两个不同的点,以所取的这三个点为顶点画三角形,画树状图求所画三角形与△ABC面积相等的概率.
答案
一.选择题
1.B
【解析】
A.“明天的降水概率为80%”,只能说明有很大机会下雨,而不能说明有80%的时间降雨,故A错误;
C.“某彩票中奖概率是1%”,只能说明中奖的机会很小,故C错误;
D.小明上次的体育测试成绩与这次测试成绩并没有任何关系,故D错误.
故答案选:B.
2.B
【解析】
如图,根据正六方形的性质可得,△AOC △ABC(SSS),同理△EOC △EDC, △AFE △AOE,
所以,阴影面积=空白部分面积
所以,飞镖落在白色区域的概率为
故选B
3.C
【解析】根据题意画出树状图如下:
共有6种等可能的结果,能让两盏灯泡同时发光的有2种情况,
∴,故选C.
4.C
【解析】由题意知道,甲和乙各与丙比赛了一场.丙当了三次裁判,说明甲和乙比赛了三场,这三场中间分别是甲和丙,乙和丙比赛.因此第一,三,五场比赛是甲和乙比赛,第二,四场是甲和丙,乙和丙比赛,并且丙都输了.故第二局输者是丙.
解:由题意,知:三场比赛的对阵情况为:
第一场:甲VS乙,丙当裁判;
第二场:乙VS丙,甲当裁判;
第三场:甲VS乙,丙当裁判;
第四场:甲VS丙,乙当裁判;
第五场:乙VS甲,丙当裁判;
由于输球的人下局当裁判,因此第二场输的人是丙.
故选C.
5.A
【解析】解:∵一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都会随机的选择一条路径,
∴它有6种路径,
∵获得食物的有2种路径,
∴获得食物的概率是:
故选A.
6.C
【解析】C点落在如图所示网格中的4个格点时,△ABC为等腰三角形,所以在其余14个格点上任取一个点C,使△ABC成为轴对称图形的概率==.
故选C.
二.填空题
7.
【解析】解:∵捕捞到草鱼的频率稳定在0.5左右,
设草鱼的条数为x,可得:
;
解得:x=2400,
经检验:x=2400是原方程的解且符合实际意义
∴由题意可得,捞到鲤鱼的概率为
,
故答案为:.
8.小红
【解析】∵大圆的半径为3m,小圆半径为2m,
∴S大圆=m2,小圆面积=m2,
∴S阴影=(m2),
∴小红获胜的概率为:,而小明获胜的概率=,
∵,
∴小红获胜的可能性大.
故答案为:小红.
9.
【解析】∵正方体的面共有6个,与A相邻的面有3个,
∴A与桌面接触的概率是.
10.
【解析】用树状图列举两辆汽车行驶的方向所有可能的结果,如图所示.
由树状图可知,这两辆汽车行驶的方向共有9种等可能出现的结果,其中它们行驶的方向相同的有3种结果,所以它们行驶的方向相同的概率为.
故答案为:.
11.公平
【解析】根据题意画出树状图如下:
由图可知:共有四种等可能结果出现,其中小明获胜的有两种,小亮获胜的也有两种,
∴P(小明获胜)=,P(小亮获胜)=,
∴P(小明获胜)=P(小亮获胜),
∴该游戏是“公平”的.
故答案为公平.
12..
【解析】设BE=a,
∵E,F分别为BC,CD的中点,∴EF∥BD,EF=BD,BC=2a,∴BD=2a,
∵AP⊥EF,∴AP⊥BD,∴BO=OD,∴点P在AC上,∴PE=EF,∴PE=BM,
∴四边形BMPE是平行四边形,∴BO=BD,
∵M为BO的中点,∴BM=BD,
∵E为BC的中点,∴BC=2a,,
过M作MH⊥BC于H,
∴,∴S正方形ABCD=4a2,S四边形BMPE=a2,
∴米粒落在四边形BMPE内的概率为,
故答案为.
13.200
【解析】.
故这次投资项目期望大致可以盈利200万元.
14.
【解析】袋中有2个红球,3个白球和5个黑球,共10球,
则每次摸出一只小球不放回,在连续2次摸出的都是黑球的情况下,第3次摸出黑球的概率是:.
故答案为.
15.
【解析】
解:大正方形的边长为:,
总面积为20,
∵阴影区域的边长为2,
∴面积为2×2=4;
故飞镖落在阴影区域的概率为,
故答案为
16.
【解析】将一名只会翻译阿拉伯语用A表示,三名只会翻译英语都用B表示,一名两种语言都会翻译用C表示,画树状图得:
∵共有20种等可能的结果,该组能够翻译上述两种语言的有14种情况,
∴该组能够翻译上述两种语言的概率为:.
故答案为:
三.解答题
17.(1)万无一失必然事件;(2)胜败乃兵家常事是随机事件;
(3)水中捞月不可能事件;(4)十拿九稳随机事件;(5)海枯石烂不可能事件;
(6)守株待兔随机事件;(7)百战百胜是必然事件;(8)九死一生随机事件.
18.解:连接AE,BF,CD.
,,,
利用三角形中线的性质可得,
被分为7个面积相同的三角形,中间阴影部分的三角形的面积是的,
所以蚂蚁踩到阴影部分的概率是.
19.解:(1)中心对称图形的卡片是A和D,所以从中随机抽取1张卡片,卡片上的图案是中心对称图形的概率为,故答案为;
(2)轴对称图形的卡片是B、C、E.
画树状图如下:
由树状图知,共有20种等可能结果,其中两次所抽取的卡片恰好都是轴对称图形的有6种结果,分别是(B,C)、(B,E)、(C,B)、(C,E)、(E,B)、(E,C),
∴两次所抽取的卡片恰好都是轴对称图形的概率=.
20.解:(1)列表如下:
1 2 3
1
2
3
转盘转动共能得到36个不同点,P点落在正方形边上的有12个,则P点落在正方形边上的概率是.
故答案为36, .
(2)根据图表可得,转盘转动共能得到36个不同点,其中落在正方形外部的有20个,则P点落在正方形外部的概率是.
21.现年20岁的这种动物活到25岁的概率为=0.625,
现年25岁的这种动物活到30岁的概率为=0.6,
答:现年20岁的这种动物活到25岁的概率为0.625,现年25岁的这种动物活到30岁的概率为0.6.
22.将转盘A平均分成10分,一份是蓝色,一份是红色,其他是绿色.
则共有20种,能配成紫色的情况有两种,
∴P(配成紫色)=
23.(1)、的面积为:,
只有△DFG或△DHF的面积也为6且不与△ABC全等,
与△ABC不全等但面积相等的三角形是:△DFG或△DHF;
(2)、画树状图如图所示:
由树状图可知共有6种等可能结果, 其中与△ABC面积相等的有3种,即△DHF,△DGF,△EGF,
所以所画三角形与△ABC面积相等的概率P=
答:所画三角形与△ABC面积相等的概率为.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
