17.1 勾股定理 课件 (共23张PPT) 2023--2024学年人教版八年级数学下册
文档属性
| 名称 | 17.1 勾股定理 课件 (共23张PPT) 2023--2024学年人教版八年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 18.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-24 18:38:50 | ||
图片预览






文档简介
(共23张PPT)
勾 股 定 理
房 梅 花
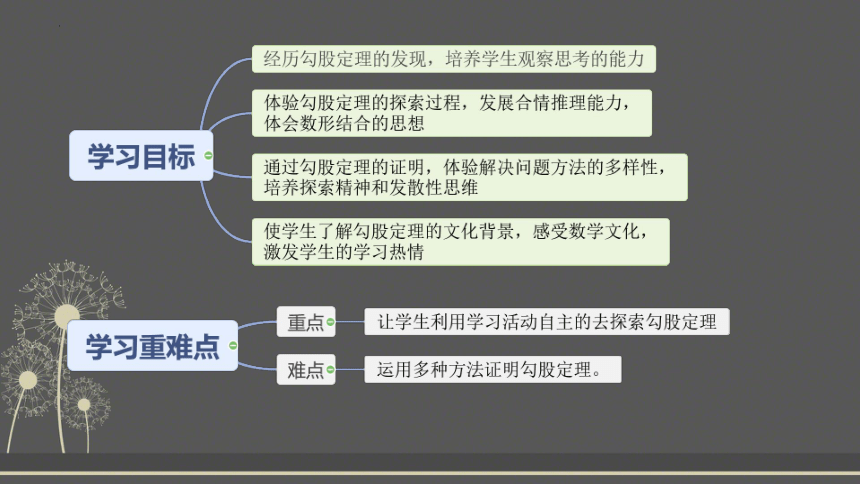
情景导入
赵爽弦图
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.
1.我们也来观察右图中的地面,看看有什么发现?
勾股定理的发现
2.这三个正方形的面积有什么关系?
3.你能发现图中三个正方形中间的等腰直角三角形的三边有什么关系吗?
+
=
c
A
B
C
图1-2
A
B
C
图1-3
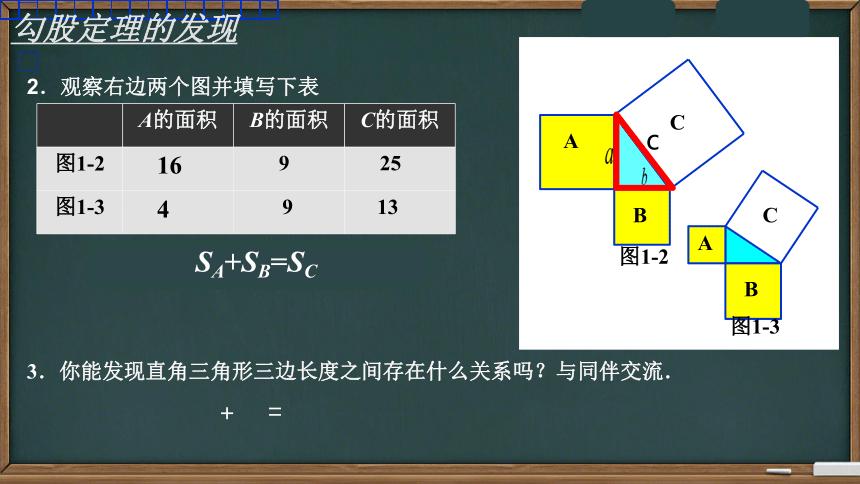
2.观察右边两个图并填写下表
A的面积 B的面积 C的面积
图1-2
图1-3
16
9
25
4
9
13
SA+SB=SC
3.你能发现直角三角形三边长度之间存在什么关系吗?与同伴交流.
勾股定理的发现
c
+
=
是不是所有的直角三角形都具有这样的特点呢?这就需要我们对一个一般的直角三角形进行证明.到目前为止,对这个命题的证明方法已有几百种之多.
勾股定理的发现
a
b
c
如果直角三角形两直角边分别
为a、b,斜边为c,那么
a +b =c
猜想
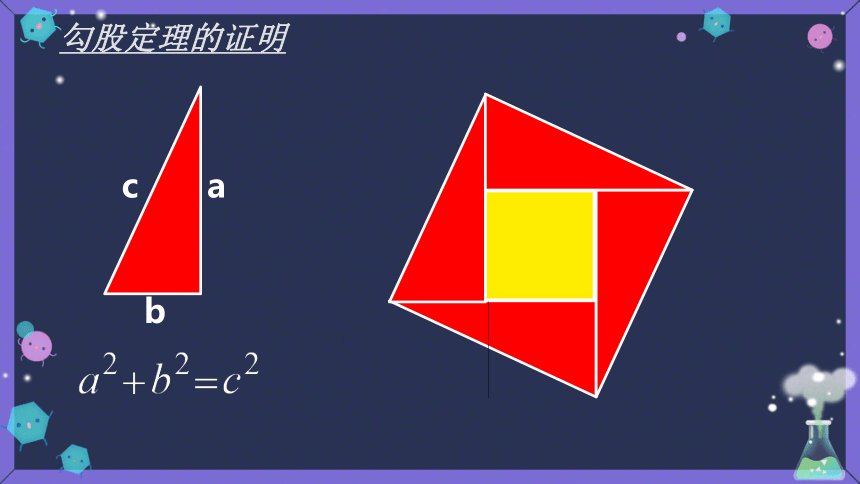
这个图案是公元 3 世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形 (黄色).
勾股定理的证明
勾股定理的证明
b
a
c
美国总统
茄菲尔得的证法:
b
c
a
b
c
a
A
B
C
D
∵ S梯形ABCD=
∴ a +b =c
勾股定理的证明
如果直角三角形两直角边分别
为a、b,斜边为c,那么
直角三角形两直角边的平方和等于斜边的平方.
勾股定理
a +b =c
a
b
c
勾
股
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾股定理的历史
商高是公元前十一世纪的西周人.在中国古代的数学著作《周髀算经》中记录着商高同周公的一段对话.
商高说:“…故折矩,勾广三,股修四,经隅五.”意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5.以后人们就简单地把这个事实说成“勾三股四弦五”.由于勾股定理的内容最早见于商高的话中,所以在我国人们就把这个定理叫作 “商高定理”
勾股定理的历史
“勾股定理”在国外,尤其在西方被称为“毕达哥拉斯定理”或“百牛定理”.毕达哥拉斯发现了勾股定理后高兴异常,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此勾股定理又叫做“百牛定理”.勾股定理流传最广的证明载于欧几里德(Euclid,是公元前三百年左右的人)的《几何原本》中,欧几里德在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为“毕达哥拉斯定理”,以后就流传开了.1955年希腊发行了一张邮票,图案是由三个棋盘排列而成.这张邮票也是为了纪念勾股定理这个伟大的发现.
1955年希腊发行的印有勾股定理图案的邮票
勾股定理的历史
宇宙探索
几十年前,有些科学家从天文望远镜中看到火星上有些地区的颜色有些季节性的变化,又看到火星上有运河模样的线条,于是就猜想火星上有高度智慧的生物存在.
当时还没有宇宙飞船,怎样和这些智慧生物取得联系呢?有人就想到,中国、希腊、埃及处在地球的不同地区,但是他们都很早并且独立的发现了勾股定理.科学家们由此推想,如果火星上有具有智慧的生物的话,他们也许能够知道勾股定理.
火星是否有高度智慧生物?现在已被基本否定,可是人类并没有打消与地球以外生物取得联系的努力.怎样跟他们联系呢?用文字他们不一定能懂.因此,我国已故著名数学家华罗庚曾建议:让宇宙飞船带着几个数学图形飞到宇宙空间,其中一个就是边长为3︰4︰5的直角三角形.同学们没想到吧,两千年前发现的勾股定理,现在在探索宇宙奥秘的过程中仍然可以发挥作用呢!
勾股定理的历史
练习1:设直角三角形的两条直角边长分别为a和b,斜边长为c。请将正确结果与相应的题目配对。
练习2:如图△ABC中AD⊥BC,AC=20,DC=16,BD=9,
求AB的长。
A
B
C
D
∟
勾股定理的应用
解 在Rt△ACD中,
在Rt△ABD中,
练习3:如图 SC=155,SB=43,SA=
C
勾股定理的应用
B
A
答案
178
课堂小结
a
b
c
收集关于勾股定理的历史与证明方法.
布置作业
感 谢 聆 听
A
B
C
图1-2
A
B
C
图1-3
SC= ×4×3×4+1
=25
割
A
B
C
图1-2
A
B
C
图1-3
SC=72 - 4× ×3×4
=25
补
勾 股 定 理
房 梅 花
情景导入
赵爽弦图
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.
1.我们也来观察右图中的地面,看看有什么发现?
勾股定理的发现
2.这三个正方形的面积有什么关系?
3.你能发现图中三个正方形中间的等腰直角三角形的三边有什么关系吗?
+
=
c
A
B
C
图1-2
A
B
C
图1-3
2.观察右边两个图并填写下表
A的面积 B的面积 C的面积
图1-2
图1-3
16
9
25
4
9
13
SA+SB=SC
3.你能发现直角三角形三边长度之间存在什么关系吗?与同伴交流.
勾股定理的发现
c
+
=
是不是所有的直角三角形都具有这样的特点呢?这就需要我们对一个一般的直角三角形进行证明.到目前为止,对这个命题的证明方法已有几百种之多.
勾股定理的发现
a
b
c
如果直角三角形两直角边分别
为a、b,斜边为c,那么
a +b =c
猜想
这个图案是公元 3 世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形 (黄色).
勾股定理的证明
勾股定理的证明
b
a
c
美国总统
茄菲尔得的证法:
b
c
a
b
c
a
A
B
C
D
∵ S梯形ABCD=
∴ a +b =c
勾股定理的证明
如果直角三角形两直角边分别
为a、b,斜边为c,那么
直角三角形两直角边的平方和等于斜边的平方.
勾股定理
a +b =c
a
b
c
勾
股
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾股定理的历史
商高是公元前十一世纪的西周人.在中国古代的数学著作《周髀算经》中记录着商高同周公的一段对话.
商高说:“…故折矩,勾广三,股修四,经隅五.”意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5.以后人们就简单地把这个事实说成“勾三股四弦五”.由于勾股定理的内容最早见于商高的话中,所以在我国人们就把这个定理叫作 “商高定理”
勾股定理的历史
“勾股定理”在国外,尤其在西方被称为“毕达哥拉斯定理”或“百牛定理”.毕达哥拉斯发现了勾股定理后高兴异常,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此勾股定理又叫做“百牛定理”.勾股定理流传最广的证明载于欧几里德(Euclid,是公元前三百年左右的人)的《几何原本》中,欧几里德在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为“毕达哥拉斯定理”,以后就流传开了.1955年希腊发行了一张邮票,图案是由三个棋盘排列而成.这张邮票也是为了纪念勾股定理这个伟大的发现.
1955年希腊发行的印有勾股定理图案的邮票
勾股定理的历史
宇宙探索
几十年前,有些科学家从天文望远镜中看到火星上有些地区的颜色有些季节性的变化,又看到火星上有运河模样的线条,于是就猜想火星上有高度智慧的生物存在.
当时还没有宇宙飞船,怎样和这些智慧生物取得联系呢?有人就想到,中国、希腊、埃及处在地球的不同地区,但是他们都很早并且独立的发现了勾股定理.科学家们由此推想,如果火星上有具有智慧的生物的话,他们也许能够知道勾股定理.
火星是否有高度智慧生物?现在已被基本否定,可是人类并没有打消与地球以外生物取得联系的努力.怎样跟他们联系呢?用文字他们不一定能懂.因此,我国已故著名数学家华罗庚曾建议:让宇宙飞船带着几个数学图形飞到宇宙空间,其中一个就是边长为3︰4︰5的直角三角形.同学们没想到吧,两千年前发现的勾股定理,现在在探索宇宙奥秘的过程中仍然可以发挥作用呢!
勾股定理的历史
练习1:设直角三角形的两条直角边长分别为a和b,斜边长为c。请将正确结果与相应的题目配对。
练习2:如图△ABC中AD⊥BC,AC=20,DC=16,BD=9,
求AB的长。
A
B
C
D
∟
勾股定理的应用
解 在Rt△ACD中,
在Rt△ABD中,
练习3:如图 SC=155,SB=43,SA=
C
勾股定理的应用
B
A
答案
178
课堂小结
a
b
c
收集关于勾股定理的历史与证明方法.
布置作业
感 谢 聆 听
A
B
C
图1-2
A
B
C
图1-3
SC= ×4×3×4+1
=25
割
A
B
C
图1-2
A
B
C
图1-3
SC=72 - 4× ×3×4
=25
补
