24.1圆的有关性质 第四课时 圆周角 圆内接四边形(含答案)
文档属性
| 名称 | 24.1圆的有关性质 第四课时 圆周角 圆内接四边形(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 371.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-24 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第2课时 圆内接四边形(原卷版)
圆内接四边形的对角互 补.
知识点:圆内接四边形的性质
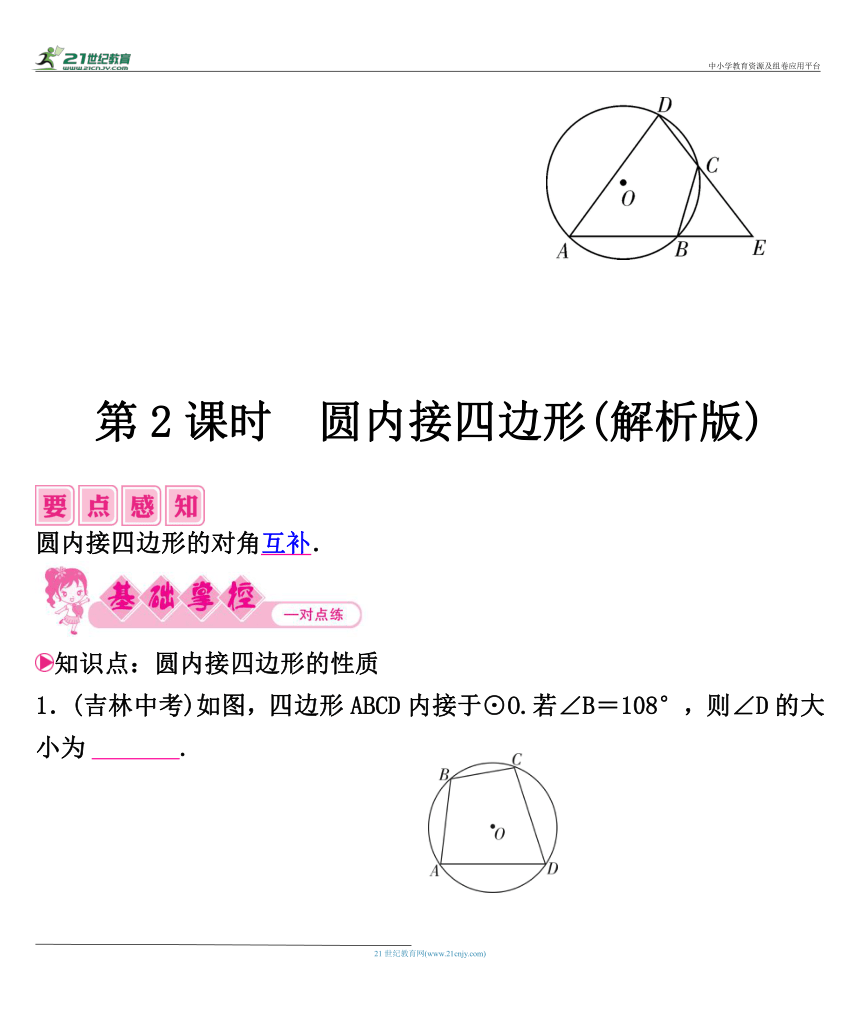
1.(吉林中考)如图,四边形ABCD内接于⊙O.若∠B=108°,则∠D的大小为72 °.
2.(昭阳一中期中)如图,在⊙O中,点D,A分别在劣弧BC和优弧BC上,∠BDC=130°,则∠BOC的度数为100 °.
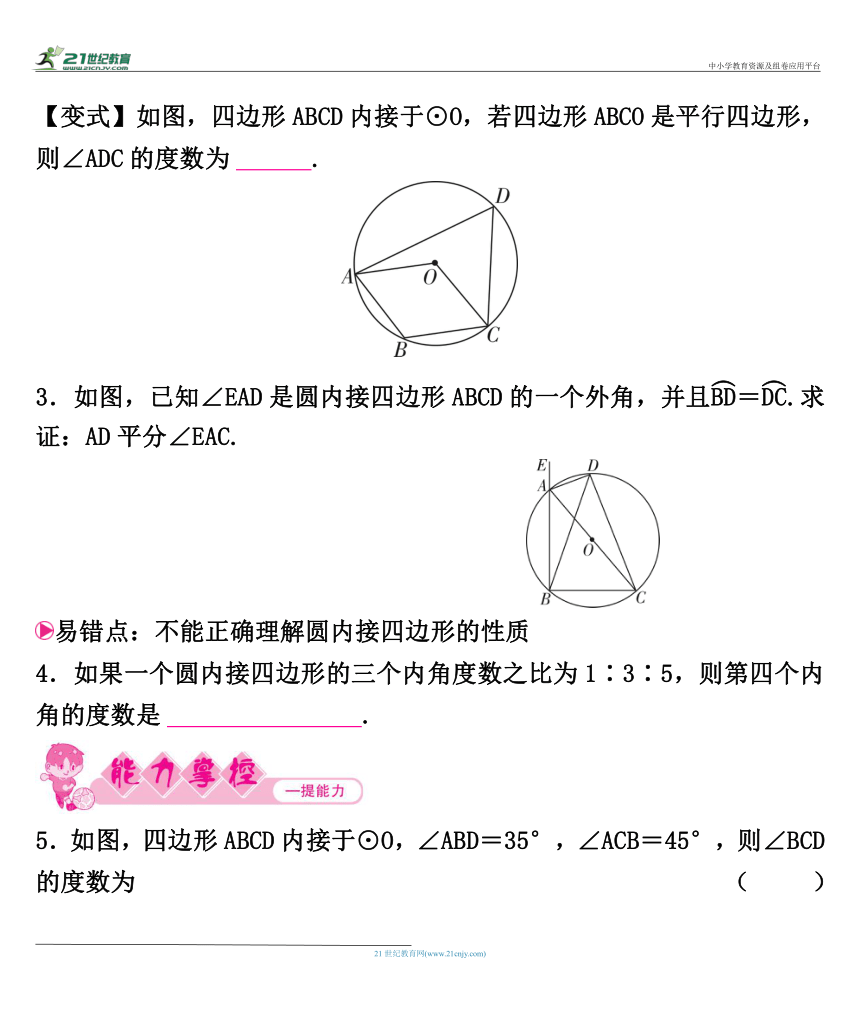
【变式】如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的度数为60 °.
3.如图,已知∠EAD是圆内接四边形ABCD的一个外角,并且=.求证:AD平分∠EAC.
易错点:不能正确理解圆内接四边形的性质
4.如果一个圆内接四边形的三个内角度数之比为1∶3∶5,则第四个内角的度数是90°或157. 5°.
5.如图,四边形ABCD内接于⊙O,∠ABD=35°,∠ACB=45°,则∠BCD的度数为 ( )
A.100°
B.90°
C.80°
D.70°
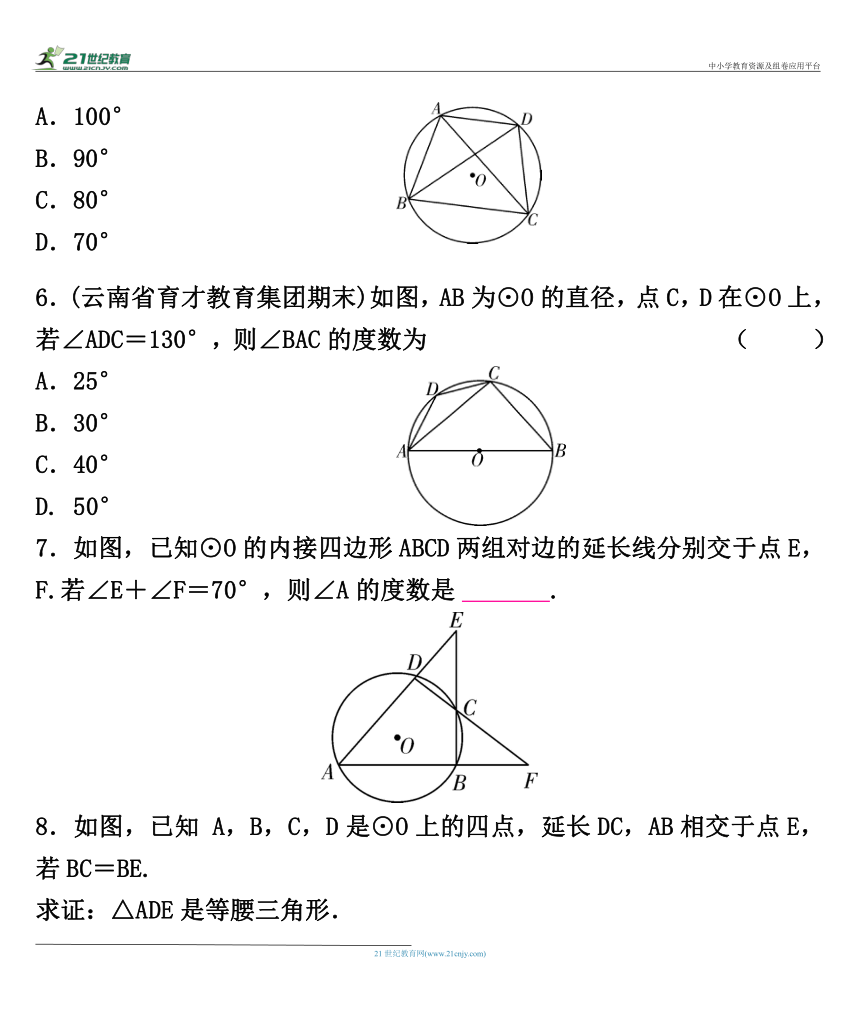
6.(云南省育才教育集团期末)如图,AB为⊙O的直径,点C,D在⊙O上,若∠ADC=130°,则∠BAC的度数为 ( )
A.25°
B.30°
C.40°
D. 50°
7.如图,已知⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F.若∠E+∠F=70°,则∠A的度数是55 °.
8.如图,已知 A,B,C,D是⊙O上的四点,延长DC,AB相交于点E,若BC=BE.
求证:△ADE是等腰三角形.
第2课时 圆内接四边形(解析版)
圆内接四边形的对角互补.
知识点:圆内接四边形的性质
1.(吉林中考)如图,四边形ABCD内接于⊙O.若∠B=108°,则∠D的大小为72 °.
答案:72°
2.(昭阳一中期中)如图,在⊙O中,点D,A分别在劣弧BC和优弧BC上,∠BDC=130°,则∠BOC的度数为100 °.
答案:100°
【变式】如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的度数为60 °.
答案:60°
3.如图,已知∠EAD是圆内接四边形ABCD的一个外角,并且=.求证:AD平分∠EAC.
证明:∵四边形ABCD是圆内接四边形,
∴∠EAD=∠DCB.
又∵=,
∴∠DAC=∠DCB.
∴∠EAD=∠DAC.
∴AD平分∠EAC.
易错点:不能正确理解圆内接四边形的性质
如果一个圆内接四边形的三个内角度数之比为1∶3∶5,则第四个内角的度数是90°或157. 5°.
答案:90°或157.5°
5.如图,四边形ABCD内接于⊙O,∠ABD=35°,∠ACB=45°,则∠BCD的度数为 ( )
A.100°
B.90°
C.80°
D.70°
答案:C
6.(云南省育才教育集团期末)如图,AB为⊙O的直径,点C,D在⊙O上,若∠ADC=130°,则∠BAC的度数为 ( )
A.25°
B.30°
C.40°
50°
答案:C
7.如图,已知⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F.若∠E+∠F=70°,则∠A的度数是55 °.
答案:55°
8.如图,已知 A,B,C,D是⊙O上的四点,延长DC,AB相交于点E,若BC=BE.
求证:△ADE是等腰三角形.
证明:∵四边形ABCD是⊙O的内接四边形,
∴∠ECB=∠A.
又∵BC=BE,
∴∠E=∠ECB,
∴∠E=∠A,∴AD=ED.
∴△ADE是等腰三角形.
21世纪教育网(www.21cnjy.com)
第2课时 圆内接四边形(原卷版)
圆内接四边形的对角互 补.
知识点:圆内接四边形的性质
1.(吉林中考)如图,四边形ABCD内接于⊙O.若∠B=108°,则∠D的大小为72 °.
2.(昭阳一中期中)如图,在⊙O中,点D,A分别在劣弧BC和优弧BC上,∠BDC=130°,则∠BOC的度数为100 °.
【变式】如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的度数为60 °.
3.如图,已知∠EAD是圆内接四边形ABCD的一个外角,并且=.求证:AD平分∠EAC.
易错点:不能正确理解圆内接四边形的性质
4.如果一个圆内接四边形的三个内角度数之比为1∶3∶5,则第四个内角的度数是90°或157. 5°.
5.如图,四边形ABCD内接于⊙O,∠ABD=35°,∠ACB=45°,则∠BCD的度数为 ( )
A.100°
B.90°
C.80°
D.70°
6.(云南省育才教育集团期末)如图,AB为⊙O的直径,点C,D在⊙O上,若∠ADC=130°,则∠BAC的度数为 ( )
A.25°
B.30°
C.40°
D. 50°
7.如图,已知⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F.若∠E+∠F=70°,则∠A的度数是55 °.
8.如图,已知 A,B,C,D是⊙O上的四点,延长DC,AB相交于点E,若BC=BE.
求证:△ADE是等腰三角形.
第2课时 圆内接四边形(解析版)
圆内接四边形的对角互补.
知识点:圆内接四边形的性质
1.(吉林中考)如图,四边形ABCD内接于⊙O.若∠B=108°,则∠D的大小为72 °.
答案:72°
2.(昭阳一中期中)如图,在⊙O中,点D,A分别在劣弧BC和优弧BC上,∠BDC=130°,则∠BOC的度数为100 °.
答案:100°
【变式】如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的度数为60 °.
答案:60°
3.如图,已知∠EAD是圆内接四边形ABCD的一个外角,并且=.求证:AD平分∠EAC.
证明:∵四边形ABCD是圆内接四边形,
∴∠EAD=∠DCB.
又∵=,
∴∠DAC=∠DCB.
∴∠EAD=∠DAC.
∴AD平分∠EAC.
易错点:不能正确理解圆内接四边形的性质
如果一个圆内接四边形的三个内角度数之比为1∶3∶5,则第四个内角的度数是90°或157. 5°.
答案:90°或157.5°
5.如图,四边形ABCD内接于⊙O,∠ABD=35°,∠ACB=45°,则∠BCD的度数为 ( )
A.100°
B.90°
C.80°
D.70°
答案:C
6.(云南省育才教育集团期末)如图,AB为⊙O的直径,点C,D在⊙O上,若∠ADC=130°,则∠BAC的度数为 ( )
A.25°
B.30°
C.40°
50°
答案:C
7.如图,已知⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F.若∠E+∠F=70°,则∠A的度数是55 °.
答案:55°
8.如图,已知 A,B,C,D是⊙O上的四点,延长DC,AB相交于点E,若BC=BE.
求证:△ADE是等腰三角形.
证明:∵四边形ABCD是⊙O的内接四边形,
∴∠ECB=∠A.
又∵BC=BE,
∴∠E=∠ECB,
∴∠E=∠A,∴AD=ED.
∴△ADE是等腰三角形.
21世纪教育网(www.21cnjy.com)
同课章节目录
