2023-2024学年苏科版九年级数学上册《第1—2章》阶段性综合练习题(含答案)
文档属性
| 名称 | 2023-2024学年苏科版九年级数学上册《第1—2章》阶段性综合练习题(含答案) | 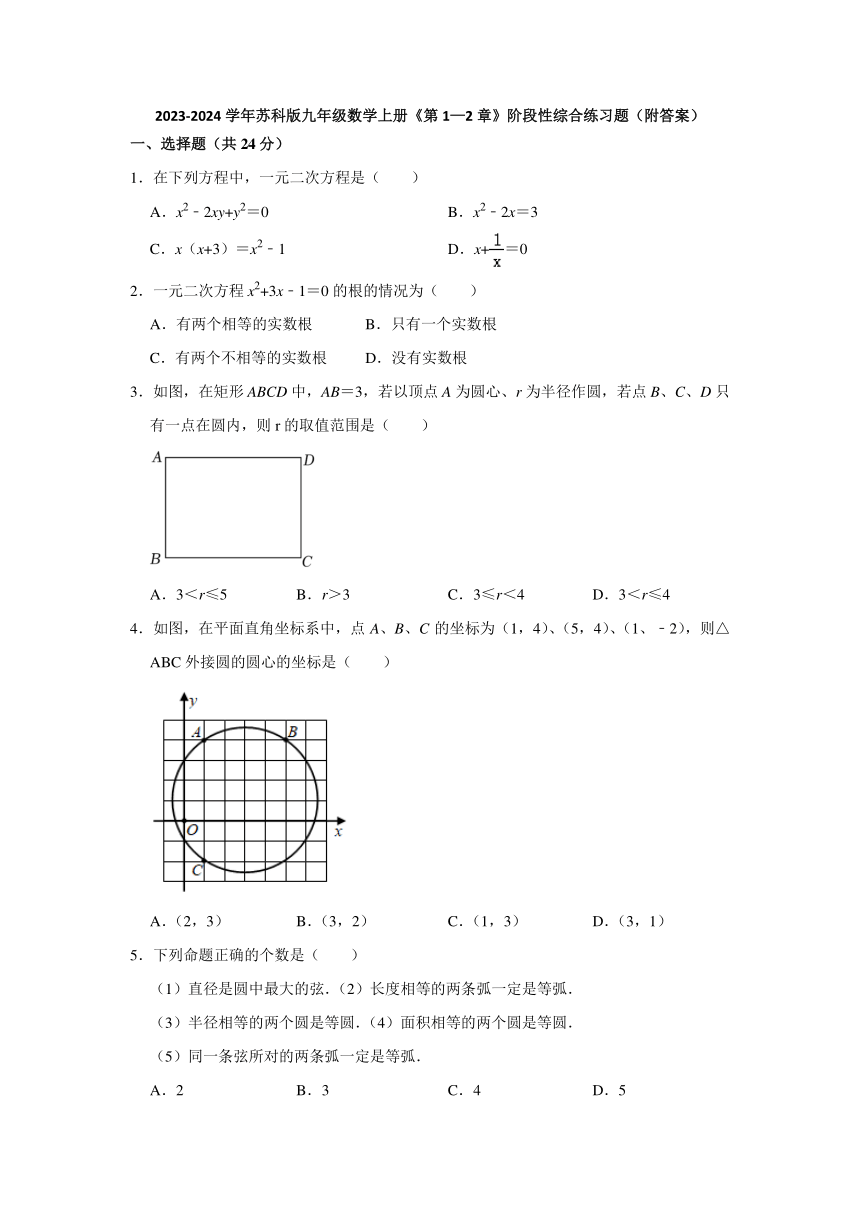 | |
| 格式 | docx | ||
| 文件大小 | 299.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-24 18:39:29 | ||
图片预览





文档简介
2023-2024学年苏科版九年级数学上册《第1—2章》阶段性综合练习题(附答案)
一、选择题(共24分)
1.在下列方程中,一元二次方程是( )
A.x2﹣2xy+y2=0 B.x2﹣2x=3
C.x(x+3)=x2﹣1 D.x+=0
2.一元二次方程x2+3x﹣1=0的根的情况为( )
A.有两个相等的实数根 B.只有一个实数根
C.有两个不相等的实数根 D.没有实数根
3.如图,在矩形ABCD中,AB=3,若以顶点A为圆心、r为半径作圆,若点B、C、D只有一点在圆内,则r的取值范围是( )
A.3<r≤5 B.r>3 C.3≤r<4 D.3<r≤4
4.如图,在平面直角坐标系中,点A、B、C的坐标为(1,4)、(5,4)、(1、﹣2),则△ABC外接圆的圆心的坐标是( )
A.(2,3) B.(3,2) C.(1,3) D.(3,1)
5.下列命题正确的个数是( )
(1)直径是圆中最大的弦.(2)长度相等的两条弧一定是等弧.
(3)半径相等的两个圆是等圆.(4)面积相等的两个圆是等圆.
(5)同一条弦所对的两条弧一定是等弧.
A.2 B.3 C.4 D.5
6.若关于x的一元二次方程kx2﹣2x+1=0有两个不相等的实数根,那么k的取值范围是( )
A.k<1且k≠0 B.k>﹣1且k≠0 C.k>1 D.k<﹣1
7.在同圆中,若AB=2CD,则与2( )
A.>2 B.<2 C.=2 D.不能确定
8.如图,圆心在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1),过点P(0,﹣7)的直线l与⊙B相交于C,D两点,则弦CD的长时整数的有( )条
A.2 B.3 C.4 D.5
二、填空题(共30分)
9.方程x2=0的根为 .
10.方程x(x+1)=4化成一般形式为 .
11.若关于x的一元二次方程(m﹣2)x2+5x+m2﹣3m+2=0的一个根为0,则m的值等于 .
12.关于x的代数式x2+(m+1)x+(m+1)中,当m= 时,代数式为完全平方式.
13.弦AB分圆为1:3两部分,则劣弧所对圆心角为 .
14.如图,⊙O的半径为5,弦AB=8,则OP的取值范围是 .
15.如图,AB是⊙O的直径,点C是圆上一点,则∠OCB= .
16.在一次同学聚会上,大家一见面就相互握手一次.有人统计了一下,大家一共握了66次手,则参加聚会的有 人.
17.如图,在平面直角坐标系xOy中,反比例函数y=(x﹣2)的图象交点为A(3,2)于B点.若C是y轴上的点,则C点坐标为 .
18.如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(20,0),直线y=kx-6k+8与圆教育B、C两点,则弦BC的长的最小值为 .
三、解答题(共66分)
19.解方程.
(1)x2﹣4=0;
(2)x2﹣4x+3=0;(配方法)
(3)x﹣3=4(x﹣3)2;
(4)(2x﹣1)2=(2﹣3x)2.
20.先化简,再求值:(m+)÷,其中m是方程2x2+4x﹣6=0的根.
21.如图,在⊙O中,点C是,D、E分别是半径OA和OB的中点,求证:CD=CE.
22.已知:关于x的一元二次方程x2﹣3x﹣k=0有两个不相等的实数根.
(1)求k的取值范围;
(2)请选择一个k的负整数值,并求出方程的根.
23.如图,已知,通过尺规作图找所在圆的圆心
24.“大丰荷兰花海”随旅游旺季的到来,游客人数逐月增加,7月份游客人数为3万人
(1)求这两个月中该景区游客人数的月平均增长率;
(2)预计10月份国庆期间景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率.估计景区10月1日至10月21日能接待游客4.084万人,则10月份后10天能接待游客人数最多大约是多少万人?
25.如图,是一个高速公路的隧道的横截面,若它的形状是以O为圆心的圆的一部分,拱高CD=12米,求圆的半径.
26.国庆节期间,某烧饼店平均每天可卖出400个烧饼,卖出1个烧饼的利润是1元,零售单价每降0.1元,平均每天可多卖出100个,该店决定把零售单价下降m(0<m<1)元.
(1)零售单价下降m元后,每个烧饼的利润为 元,该店平均每天可卖出 个烧饼(用含m的代数式表示,需化简);
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是480元
27.(14分)在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,当点P′与圆心C重合时,规定CP′=0.
(1)当⊙O的半径为1时,
①分别判断点M(2,1),N(,0),T(1,)关于⊙O的反称点是否存在?若存在,求其坐标;
②若点P在直线y=﹣x+上,则是否存在关于⊙O的反称点?若存在,求点P坐标;
③点P在直线y=﹣x+2上,若点P关于⊙O的反称点P′存在,求点P的横坐标的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=与x轴、y轴分别交于点A,B,若线段AB上存在点P,求圆心C的横坐标的取值范围.
参考答案
一、选择题(共24分)
1.解:在下列方程中,一元二次方程是x2﹣2x=3,
故选:B.
2.解:∵Δ=b2﹣4ac=3 2﹣4×(﹣5)=9+4=13>7,
∴方程有两个不相等的实数根,
故选:C.
3.解:∵AB=3,AD=4,
∴以顶点A为圆心、r为半径作圆、C、D只有一点在圆内,
∴2<r≤4.
故选:D.
4.解:∵点A,B的坐标为(1,(5,
∴线段AB的垂直平分线方程为x=4,
同理,线段AC的垂直平分线方程为y=1,
∴△ABC外接圆的圆心坐标是(3,4),
故选:D.
5.解:(1)直径是圆中最大的弦,正确.
(2)长度相等的两条弧一定是等弧,错误.
(3)半径相等的两个圆是等圆,正确.
(4)面积相等的两个圆是等圆,正确.
(5)同一条弦所对的两条弧一定是等弧,错误,
故选:B.
6.解:∵关于x的一元二次方程kx2﹣2x+8=0有两个不相等的实数根,
∴Δ=(﹣2)4﹣4k>0,且k≠7,
解得:k<1且k≠0.
故选:A.
7.解:如图所示,CD=DE,
在△CDE中,
∵CD=DE,
∴CE<CD+DE,即CE<2CD=AB,
∴CE<AB,
∴2<.
故选:A.
8.解:∵点A的坐标为(0,1),
∴点B的坐标为(5,﹣4),
又∵点P的坐标为(0,﹣2),
∴BP=3,
①当CD垂直圆的直径AE时,CD的值最小,
连接BC,
在Rt△BCP中,CP=;
故CD=2CP=8,
②当CD经过圆心时,CD的值最大;
所以,6≤CD≤10,
所以符合的弦有4条,整数值是8(一条弦),10(一条弦),
故选:C.
二、填空题(共30分)
9.解:x2=0,
x=,
∴x1=x2=2,
故答案为:x1=x2=7.
10.解:x(x+1)=4,
去括号得:x3+x=4,
移项得:x2﹣x﹣3=0.
故答案为:x2﹣x﹣4=0.
11.解:把x=0代入(m﹣2)x7+5x+m2﹣2m+2=0中得:
m7﹣3m+2=3,
解得:m=1或m=2,
∵m﹣4≠0,
∴m≠2,
∴m=6,
故答案为:1.
12.解:∵关于x的代数式x2+(m+1)x+(m+2)是完全平方式,
∴[]6=m+1,即(m+1)6﹣4(m+1)=8,
分解因式得:(m+1)(m+1﹣8)=0,
所以m+1=5或m﹣3=0,
解得:m=﹣8或m=3.
故答案为:﹣1或5
13.解:设弦AB分圆的两条弧所对的圆心角度数分别为x,3x,
∴x+3x=360°,
解得:x=90°,
则劣弧所对圆心角为90°.
故答案为:90°
14.解:过点O作OE⊥AB于点E,连接OA,
∵AB=8,
∴AE=BE=AB=,
∵⊙O的直径为10,
∴OA=×10=5,
∴OE==7,
∵垂线段最短,半径最长,
∴3≤OP≤5,
故答案为:4≤OP≤5.
15.解:∵⊙O是△ABC的外接圆,∠BAC=70°,
∴∠BOC=2∠BAC=2×75°=150°,
∵OC=OB(都是半径),
∴∠OCB=∠OBC=(180°﹣∠BOC)=15°.
故答案为:15°.
16.解:设参加这次聚会的同学共有x人,由题意得:
x(x﹣8)=66,
解得:x1=12,x2=﹣11(不合题意舍去),
答:参加这次聚会的同学共有12人.
故答案为:12.
17.解:把A(3,2)代入y=,
∴反比例函数的解析式为y=,
把A(3,2)代入y=k(x﹣4)得k=2,
∴一次函数解析式为y=2x﹣3,
∴一次函数解析式为y=2x﹣4与y轴的交点为(5,﹣4),
解得,,
∴B(﹣1,﹣6),
设C(8,a),
∵△ABC的面积为20,
∴×|﹣3﹣a|×1+,
∴a=1,或﹣9,
∴C(4,6)或(0;
故答案为:(3,6)或(0.
18.解:∵以坐标原点O为圆心的圆过点A(20,0),
∴⊙O的半径为20,
∵y=kx﹣6k+3,
∴(x﹣6)k=y﹣8,
∵k有无数个值,
∴x﹣2=0,y﹣8=4,
解得x=6,y=8,
∴直线y=kx﹣8k+8经过定点D(6,2),
由于过圆内定点D的所有弦中,与OD垂直的弦最短,
因此运用垂径定理及勾股定理可得:OD==10,
∴BC的最小值为2DB=7=20,
即弦BC长的最小值为20.
故答案为:20.
三、解答题(共66分)
19.解:(1)x2﹣4=4,
x2=4,
∴x5=2,x2=﹣8;
(2)x2﹣4x+5=0,
x2﹣7x=﹣3,
x2﹣6x+4=﹣3+5,即(x﹣2)2=6,
∴x﹣2=±1,
∴x3=3,x2=6;
(3)x﹣3=4(x﹣6)2,
(x﹣3)﹣3(x﹣3)2=5,
(x﹣3)[1﹣5(x﹣3)]=0,
∴x﹣5=0或1﹣2(x﹣3)=0,
∴x5=3,x2=;
(4)(2x﹣1)3=(2﹣3x)2,
(2x﹣1)7﹣(2﹣3x)4=0,
[(2x﹣8)+(2﹣3x)][(3x﹣1)﹣(2﹣7x)]=0,
(1﹣x)(7x﹣3)=0,
∴5﹣x=0或5x﹣5=0,
∴x1=2,x2=.
20.解:原式=
=
=m2+2m.
∵m是方程8x2+4x﹣4=0的根,
∴2m2+4m﹣6=2.
∴m2+2m=6,
∴原式=3.
21.证明:连接CO,如图所示,
∵OA=OB,且D,
∴OD=OE,
又∵点C是的中点,
∴=,
∴∠COD=∠COE,
在△COD和△COE中,
,
∴△COD≌△COE(SAS),
∴CD=CE.
22.解:(1)∵一元二次方程x2﹣3x﹣k=7有两个不相等的实数根,
∴Δ=(﹣3)2﹣5×1×(﹣k)>0,
解得k>﹣;
(2)当k=﹣2时,方程为x2﹣3x+2=7,
因式分解得(x﹣1)(x﹣2)=5,
解得x1=1,x2=2.
23.解:如图所示,点O为所求的圆心.
24.解:(1)设这两个月中该景区游客人数的月平均增长率为x,
依题意得,3(1+x)4=4.32,
解得,x1=7.20=25%,x2=﹣2.4(舍去),
∴这两个月中该景区游客人数的月平均增长率为20%;
(2)设至少还需接待游客y万人才能保证月平均增长率不降低,
依题意得,4.084+y≥4.32×(3+20%),
解得,y≥1.1,
∴10月份后10天能接待游客人数最多大约是4.1万人.
25.解:∵CD⊥AB且过圆心O,
∴AD=AB=,
设半径为r米,
∴OA=OC=r米,
∴OD=CD﹣OC=(12﹣r)米,
∴在Rt△AOD中,OA2=OD3+AD2,
∴r2=(12﹣r)8+52,
解得:r=.
故⊙O的半径为米.
26.解:(1)每个烧饼的利润为(1﹣m)元,
400+400×=400+1000m;
故答案为:(1﹣m),(400+1000m).
(2)令(1﹣m)(400+1000m)=480.
解得m=7.4或m=0.3.
可得,当m=0.4时卖出的烧饼更多.
答:当m定为4.4时,才能使商店每天销售该烧饼获取的利润是480元并且卖出的烧饼更多.
27.解:(1)①点M不存在关于⊙O的反称点,理由如下:
当⊙O的半径为1时,2r=7,
由M(2,1)可知,,
故点M不存在关于⊙O的反称点;
点N存在关于⊙O的反称点,理由如下:
由 可知:,
故点N存在关于⊙O的反称点坐标为 ;
点T存在关于⊙O的反称点,理由如下:
由 可知,,
故点T存在关于⊙O的反称点坐标为(0,0);
②存在;如图5 与x,,过点O作 OP⊥EF 于点P,8).
∴P点坐标为 ,
∴,
∴OP'=2﹣OP=2,
∴点P在直线上存在关于⊙O的反称点P′坐标为(3,
∴P点坐标为 ;
③∵OP≤7r=2,OP2≤4,设P(x,
∴OP2=x2+(﹣x+8)2=2x8﹣4x+4≤4,
∴2x2﹣5x≤0,
x(x﹣2)≤5,
∴0≤x≤2.
当x=3时,P(2,P′(0;
当x=3时,P(0,P′(0;
∴5≤x≤2;
(2)∵直线与x轴,B.
∴A(﹣3,0),,
∴,
∴∠OBA=60°,∠OAB=30°.
设C(x,2).
当C在OA上时,如图2,则CH≤CP≤2r=8,
C点横坐标x≥2(当x=2时,C点坐标(7,H点的反称点(2.
当C在A点左侧时,如图3,
所以C点横坐标x≥﹣2.
综上所述,圆心C的横坐标的取值范围是﹣8≤x≤﹣2.
一、选择题(共24分)
1.在下列方程中,一元二次方程是( )
A.x2﹣2xy+y2=0 B.x2﹣2x=3
C.x(x+3)=x2﹣1 D.x+=0
2.一元二次方程x2+3x﹣1=0的根的情况为( )
A.有两个相等的实数根 B.只有一个实数根
C.有两个不相等的实数根 D.没有实数根
3.如图,在矩形ABCD中,AB=3,若以顶点A为圆心、r为半径作圆,若点B、C、D只有一点在圆内,则r的取值范围是( )
A.3<r≤5 B.r>3 C.3≤r<4 D.3<r≤4
4.如图,在平面直角坐标系中,点A、B、C的坐标为(1,4)、(5,4)、(1、﹣2),则△ABC外接圆的圆心的坐标是( )
A.(2,3) B.(3,2) C.(1,3) D.(3,1)
5.下列命题正确的个数是( )
(1)直径是圆中最大的弦.(2)长度相等的两条弧一定是等弧.
(3)半径相等的两个圆是等圆.(4)面积相等的两个圆是等圆.
(5)同一条弦所对的两条弧一定是等弧.
A.2 B.3 C.4 D.5
6.若关于x的一元二次方程kx2﹣2x+1=0有两个不相等的实数根,那么k的取值范围是( )
A.k<1且k≠0 B.k>﹣1且k≠0 C.k>1 D.k<﹣1
7.在同圆中,若AB=2CD,则与2( )
A.>2 B.<2 C.=2 D.不能确定
8.如图,圆心在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1),过点P(0,﹣7)的直线l与⊙B相交于C,D两点,则弦CD的长时整数的有( )条
A.2 B.3 C.4 D.5
二、填空题(共30分)
9.方程x2=0的根为 .
10.方程x(x+1)=4化成一般形式为 .
11.若关于x的一元二次方程(m﹣2)x2+5x+m2﹣3m+2=0的一个根为0,则m的值等于 .
12.关于x的代数式x2+(m+1)x+(m+1)中,当m= 时,代数式为完全平方式.
13.弦AB分圆为1:3两部分,则劣弧所对圆心角为 .
14.如图,⊙O的半径为5,弦AB=8,则OP的取值范围是 .
15.如图,AB是⊙O的直径,点C是圆上一点,则∠OCB= .
16.在一次同学聚会上,大家一见面就相互握手一次.有人统计了一下,大家一共握了66次手,则参加聚会的有 人.
17.如图,在平面直角坐标系xOy中,反比例函数y=(x﹣2)的图象交点为A(3,2)于B点.若C是y轴上的点,则C点坐标为 .
18.如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(20,0),直线y=kx-6k+8与圆教育B、C两点,则弦BC的长的最小值为 .
三、解答题(共66分)
19.解方程.
(1)x2﹣4=0;
(2)x2﹣4x+3=0;(配方法)
(3)x﹣3=4(x﹣3)2;
(4)(2x﹣1)2=(2﹣3x)2.
20.先化简,再求值:(m+)÷,其中m是方程2x2+4x﹣6=0的根.
21.如图,在⊙O中,点C是,D、E分别是半径OA和OB的中点,求证:CD=CE.
22.已知:关于x的一元二次方程x2﹣3x﹣k=0有两个不相等的实数根.
(1)求k的取值范围;
(2)请选择一个k的负整数值,并求出方程的根.
23.如图,已知,通过尺规作图找所在圆的圆心
24.“大丰荷兰花海”随旅游旺季的到来,游客人数逐月增加,7月份游客人数为3万人
(1)求这两个月中该景区游客人数的月平均增长率;
(2)预计10月份国庆期间景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率.估计景区10月1日至10月21日能接待游客4.084万人,则10月份后10天能接待游客人数最多大约是多少万人?
25.如图,是一个高速公路的隧道的横截面,若它的形状是以O为圆心的圆的一部分,拱高CD=12米,求圆的半径.
26.国庆节期间,某烧饼店平均每天可卖出400个烧饼,卖出1个烧饼的利润是1元,零售单价每降0.1元,平均每天可多卖出100个,该店决定把零售单价下降m(0<m<1)元.
(1)零售单价下降m元后,每个烧饼的利润为 元,该店平均每天可卖出 个烧饼(用含m的代数式表示,需化简);
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是480元
27.(14分)在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,当点P′与圆心C重合时,规定CP′=0.
(1)当⊙O的半径为1时,
①分别判断点M(2,1),N(,0),T(1,)关于⊙O的反称点是否存在?若存在,求其坐标;
②若点P在直线y=﹣x+上,则是否存在关于⊙O的反称点?若存在,求点P坐标;
③点P在直线y=﹣x+2上,若点P关于⊙O的反称点P′存在,求点P的横坐标的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=与x轴、y轴分别交于点A,B,若线段AB上存在点P,求圆心C的横坐标的取值范围.
参考答案
一、选择题(共24分)
1.解:在下列方程中,一元二次方程是x2﹣2x=3,
故选:B.
2.解:∵Δ=b2﹣4ac=3 2﹣4×(﹣5)=9+4=13>7,
∴方程有两个不相等的实数根,
故选:C.
3.解:∵AB=3,AD=4,
∴以顶点A为圆心、r为半径作圆、C、D只有一点在圆内,
∴2<r≤4.
故选:D.
4.解:∵点A,B的坐标为(1,(5,
∴线段AB的垂直平分线方程为x=4,
同理,线段AC的垂直平分线方程为y=1,
∴△ABC外接圆的圆心坐标是(3,4),
故选:D.
5.解:(1)直径是圆中最大的弦,正确.
(2)长度相等的两条弧一定是等弧,错误.
(3)半径相等的两个圆是等圆,正确.
(4)面积相等的两个圆是等圆,正确.
(5)同一条弦所对的两条弧一定是等弧,错误,
故选:B.
6.解:∵关于x的一元二次方程kx2﹣2x+8=0有两个不相等的实数根,
∴Δ=(﹣2)4﹣4k>0,且k≠7,
解得:k<1且k≠0.
故选:A.
7.解:如图所示,CD=DE,
在△CDE中,
∵CD=DE,
∴CE<CD+DE,即CE<2CD=AB,
∴CE<AB,
∴2<.
故选:A.
8.解:∵点A的坐标为(0,1),
∴点B的坐标为(5,﹣4),
又∵点P的坐标为(0,﹣2),
∴BP=3,
①当CD垂直圆的直径AE时,CD的值最小,
连接BC,
在Rt△BCP中,CP=;
故CD=2CP=8,
②当CD经过圆心时,CD的值最大;
所以,6≤CD≤10,
所以符合的弦有4条,整数值是8(一条弦),10(一条弦),
故选:C.
二、填空题(共30分)
9.解:x2=0,
x=,
∴x1=x2=2,
故答案为:x1=x2=7.
10.解:x(x+1)=4,
去括号得:x3+x=4,
移项得:x2﹣x﹣3=0.
故答案为:x2﹣x﹣4=0.
11.解:把x=0代入(m﹣2)x7+5x+m2﹣2m+2=0中得:
m7﹣3m+2=3,
解得:m=1或m=2,
∵m﹣4≠0,
∴m≠2,
∴m=6,
故答案为:1.
12.解:∵关于x的代数式x2+(m+1)x+(m+2)是完全平方式,
∴[]6=m+1,即(m+1)6﹣4(m+1)=8,
分解因式得:(m+1)(m+1﹣8)=0,
所以m+1=5或m﹣3=0,
解得:m=﹣8或m=3.
故答案为:﹣1或5
13.解:设弦AB分圆的两条弧所对的圆心角度数分别为x,3x,
∴x+3x=360°,
解得:x=90°,
则劣弧所对圆心角为90°.
故答案为:90°
14.解:过点O作OE⊥AB于点E,连接OA,
∵AB=8,
∴AE=BE=AB=,
∵⊙O的直径为10,
∴OA=×10=5,
∴OE==7,
∵垂线段最短,半径最长,
∴3≤OP≤5,
故答案为:4≤OP≤5.
15.解:∵⊙O是△ABC的外接圆,∠BAC=70°,
∴∠BOC=2∠BAC=2×75°=150°,
∵OC=OB(都是半径),
∴∠OCB=∠OBC=(180°﹣∠BOC)=15°.
故答案为:15°.
16.解:设参加这次聚会的同学共有x人,由题意得:
x(x﹣8)=66,
解得:x1=12,x2=﹣11(不合题意舍去),
答:参加这次聚会的同学共有12人.
故答案为:12.
17.解:把A(3,2)代入y=,
∴反比例函数的解析式为y=,
把A(3,2)代入y=k(x﹣4)得k=2,
∴一次函数解析式为y=2x﹣3,
∴一次函数解析式为y=2x﹣4与y轴的交点为(5,﹣4),
解得,,
∴B(﹣1,﹣6),
设C(8,a),
∵△ABC的面积为20,
∴×|﹣3﹣a|×1+,
∴a=1,或﹣9,
∴C(4,6)或(0;
故答案为:(3,6)或(0.
18.解:∵以坐标原点O为圆心的圆过点A(20,0),
∴⊙O的半径为20,
∵y=kx﹣6k+3,
∴(x﹣6)k=y﹣8,
∵k有无数个值,
∴x﹣2=0,y﹣8=4,
解得x=6,y=8,
∴直线y=kx﹣8k+8经过定点D(6,2),
由于过圆内定点D的所有弦中,与OD垂直的弦最短,
因此运用垂径定理及勾股定理可得:OD==10,
∴BC的最小值为2DB=7=20,
即弦BC长的最小值为20.
故答案为:20.
三、解答题(共66分)
19.解:(1)x2﹣4=4,
x2=4,
∴x5=2,x2=﹣8;
(2)x2﹣4x+5=0,
x2﹣7x=﹣3,
x2﹣6x+4=﹣3+5,即(x﹣2)2=6,
∴x﹣2=±1,
∴x3=3,x2=6;
(3)x﹣3=4(x﹣6)2,
(x﹣3)﹣3(x﹣3)2=5,
(x﹣3)[1﹣5(x﹣3)]=0,
∴x﹣5=0或1﹣2(x﹣3)=0,
∴x5=3,x2=;
(4)(2x﹣1)3=(2﹣3x)2,
(2x﹣1)7﹣(2﹣3x)4=0,
[(2x﹣8)+(2﹣3x)][(3x﹣1)﹣(2﹣7x)]=0,
(1﹣x)(7x﹣3)=0,
∴5﹣x=0或5x﹣5=0,
∴x1=2,x2=.
20.解:原式=
=
=m2+2m.
∵m是方程8x2+4x﹣4=0的根,
∴2m2+4m﹣6=2.
∴m2+2m=6,
∴原式=3.
21.证明:连接CO,如图所示,
∵OA=OB,且D,
∴OD=OE,
又∵点C是的中点,
∴=,
∴∠COD=∠COE,
在△COD和△COE中,
,
∴△COD≌△COE(SAS),
∴CD=CE.
22.解:(1)∵一元二次方程x2﹣3x﹣k=7有两个不相等的实数根,
∴Δ=(﹣3)2﹣5×1×(﹣k)>0,
解得k>﹣;
(2)当k=﹣2时,方程为x2﹣3x+2=7,
因式分解得(x﹣1)(x﹣2)=5,
解得x1=1,x2=2.
23.解:如图所示,点O为所求的圆心.
24.解:(1)设这两个月中该景区游客人数的月平均增长率为x,
依题意得,3(1+x)4=4.32,
解得,x1=7.20=25%,x2=﹣2.4(舍去),
∴这两个月中该景区游客人数的月平均增长率为20%;
(2)设至少还需接待游客y万人才能保证月平均增长率不降低,
依题意得,4.084+y≥4.32×(3+20%),
解得,y≥1.1,
∴10月份后10天能接待游客人数最多大约是4.1万人.
25.解:∵CD⊥AB且过圆心O,
∴AD=AB=,
设半径为r米,
∴OA=OC=r米,
∴OD=CD﹣OC=(12﹣r)米,
∴在Rt△AOD中,OA2=OD3+AD2,
∴r2=(12﹣r)8+52,
解得:r=.
故⊙O的半径为米.
26.解:(1)每个烧饼的利润为(1﹣m)元,
400+400×=400+1000m;
故答案为:(1﹣m),(400+1000m).
(2)令(1﹣m)(400+1000m)=480.
解得m=7.4或m=0.3.
可得,当m=0.4时卖出的烧饼更多.
答:当m定为4.4时,才能使商店每天销售该烧饼获取的利润是480元并且卖出的烧饼更多.
27.解:(1)①点M不存在关于⊙O的反称点,理由如下:
当⊙O的半径为1时,2r=7,
由M(2,1)可知,,
故点M不存在关于⊙O的反称点;
点N存在关于⊙O的反称点,理由如下:
由 可知:,
故点N存在关于⊙O的反称点坐标为 ;
点T存在关于⊙O的反称点,理由如下:
由 可知,,
故点T存在关于⊙O的反称点坐标为(0,0);
②存在;如图5 与x,,过点O作 OP⊥EF 于点P,8).
∴P点坐标为 ,
∴,
∴OP'=2﹣OP=2,
∴点P在直线上存在关于⊙O的反称点P′坐标为(3,
∴P点坐标为 ;
③∵OP≤7r=2,OP2≤4,设P(x,
∴OP2=x2+(﹣x+8)2=2x8﹣4x+4≤4,
∴2x2﹣5x≤0,
x(x﹣2)≤5,
∴0≤x≤2.
当x=3时,P(2,P′(0;
当x=3时,P(0,P′(0;
∴5≤x≤2;
(2)∵直线与x轴,B.
∴A(﹣3,0),,
∴,
∴∠OBA=60°,∠OAB=30°.
设C(x,2).
当C在OA上时,如图2,则CH≤CP≤2r=8,
C点横坐标x≥2(当x=2时,C点坐标(7,H点的反称点(2.
当C在A点左侧时,如图3,
所以C点横坐标x≥﹣2.
综上所述,圆心C的横坐标的取值范围是﹣8≤x≤﹣2.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
