第11章三角形 同步练习题(含答案) 2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 第11章三角形 同步练习题(含答案) 2024—2025学年人教版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 687.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-24 00:00:00 | ||
图片预览




文档简介
2023-2024学年人教版八年级数学上册《第11章三角形》同步练习题(附答案)
一、单选题
1.已知一个三角形的三边长分别为2、4、x,那么的取值可以是( )
A.1 B.2 C.4 D.7
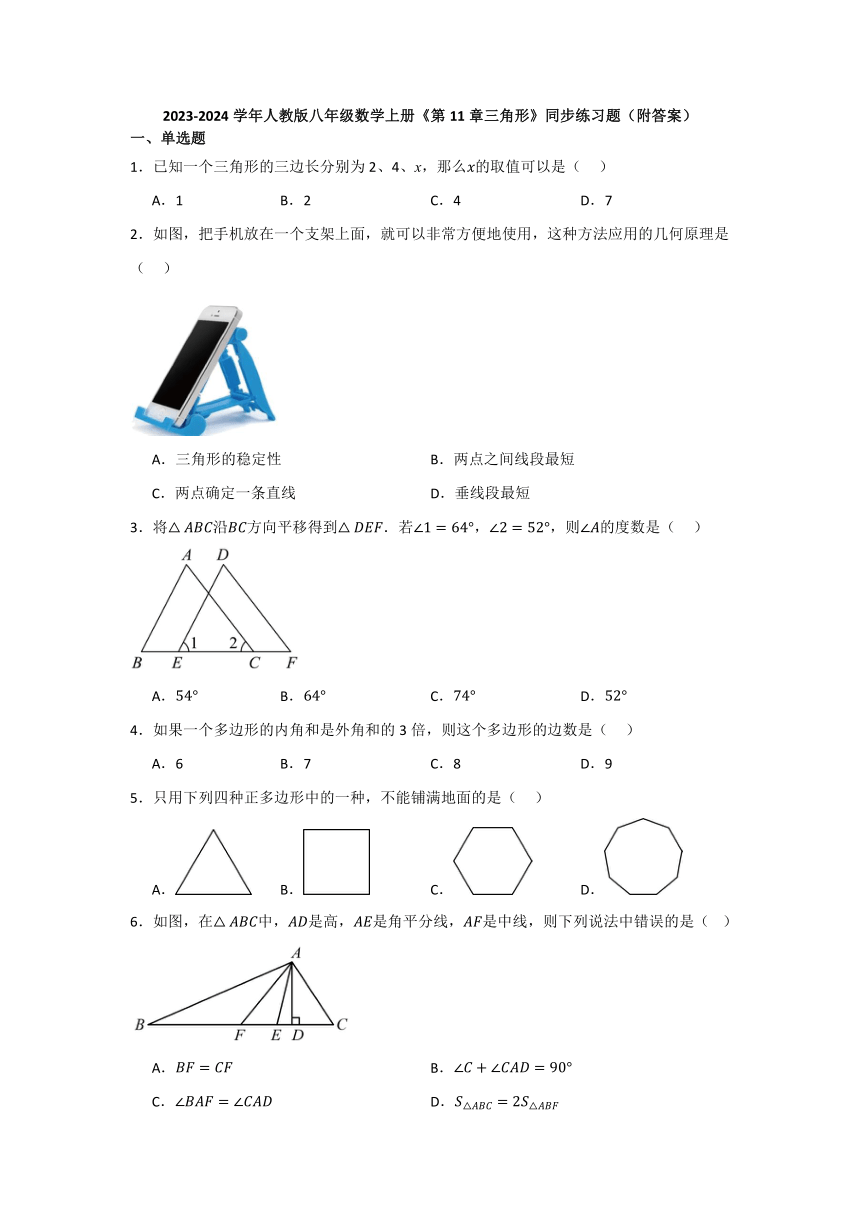
2.如图,把手机放在一个支架上面,就可以非常方便地使用,这种方法应用的几何原理是( )
A.三角形的稳定性 B.两点之间线段最短
C.两点确定一条直线 D.垂线段最短
3.将沿方向平移得到.若,,则的度数是( )
A. B. C. D.
4.如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )
A.6 B.7 C.8 D.9
5.只用下列四种正多边形中的一种,不能铺满地面的是( )
A. B. C. D.
6.如图,在中,是高,是角平分线,是中线,则下列说法中错误的是( )
A. B.
C. D.
7.如图,为的中线,为的中线.若的面积为10,则的面积为( )
A.40 B.30 C.20 D.15
8.五边形的边所在直线形成如图所示的形状,则( )
A. B. C. D.
二、填空题
9.如图,E是边的中点,若,的周长比的周长多1,则 .
10.已知中,为边上的高,,则 .
11.如图,在中,点D是边的中点,点E是边上一点,和交于点O,,的面积是2024,若把的面积记为,把四边形的面积记为,则的值为 .
12.将一个正五边形和一个正六边形按如图所示的方式放在直线上,连接正五边形的对角线,则的度数为 .
13.如图,中,,,平分,于D,,则的度数 .
14.如图,的度数是 .
15.如图是可调躺椅示意图(数据如图),与的交点为,且,,保持不变.为了舒适,可调整的大小,使,则图中应 (填“增加”或“减少”) 度.
16.如图,,,延长至点,连接,和的角平分线交于点,下列三个结论:①;②;③若,,则.其中结论正确的个数有 .
三、解答题
17.已知a、b、c是一个三角形的三边长.
(1)若,,则c的取值范围是_______.
(2)试化简:.
18.根据下列对话,回答问题:
宝宝:我把一个多边形的各内角相加,所得的和为;
贝贝:什么?不可能的!你错把一个外角当作内角了!
(1)多边形的内角和为,为什么不可能?
(2)宝宝求的是几边形的内角和?
19.如图,方格纸中每个小正方形边长均为1,在方格纸内将的点C平移至点得到.
(1)画出;
(2)线段和的关系是_______.
(3)借助方格画出边上的中线和高;
(4)四边形 面积为_______.
20.【探究学习】小学阶段,我们可以通过“拼”角、“折”角,观察得到三角形内角和为 ,现在我们学行线的性质,就可以证明此结论的正确性了.
(1)如图1,过 的顶点作的平行线,请你证明三角形的内角和为
证明:因为,
所以 ( ).
因为( ).
所以 (等量代换),
即三角形的内角和为.
【解题反思】
平行线具有“等角转化”的功能.
【迁移应用】
(2)近年来,我国一直提倡“绿色环保、低碳生活”,健康骑行越来越受到老百姓的喜欢.自行车的示意图如图2,其中.若,,则的度数为 .
21.如图,在中,平分交于点,点为直线上一点,连接,,连接交于点,作平分交于点.
(1)求证:;
(2)若.
①试判断,,之间的数量关系,并说明理由;
②若,求的度数.
22.(1)如图1,在中,,,的平分线相交于点P,求;
(2)如图2,在中,,的外角,的平分线相交于点P,求;
(3)如图3,的的平分线与其外角的平分线相交于点P,若,求的度数.(用含的代数式表示)
参考答案
1.解:由三角形三边关系定理得,
解得:,
四个选项中符合题意的只有4.
故选:C.
2.解:把手机放在一个支架上面,手机和支架形成了一个三角形,
因此这里所用的几何原理是:三角形的稳定性,
故选A.
3.解:根据题意,由平移的性质得:,
∴,
故选:B .
4.解:多边形的外角和是,根据题意得:
解得.
故选C.
5.解:A、正三角形的每个内角的度数为,且,则能铺满地面,此项不符题意;
B、正四边形的每个内角的度数为,且,则能铺满地面,此项不符题意;
C、正六边形的每个内角的度数为,且,则能铺满地面,此项不符题意;
D、正九边形的每个内角的度数为,且,则不能铺满地面,此项符题意;
故选:D.
6.解:∵是的中线,
,A说法正确,不符合题意;
是高,
,
,B说法正确,不符合题意;
是角平分线,
,而与不一定相等,C说法错误,符合题意;
,
,D说法正确,不符合题意;
故选:C.
7.解:∵为的中线.的面积为10,
∴,
∵为的中线,
∴,
故选:A.
8.解:如图所示,
∵,,
又∵,
∴.
故选:C.
9.解:E是边的中点,
,
的周长比的周长多1,且,
,
即,
,
故答案为:5.
10.解:①如图,当在的内部时,
,
②如图,当在的外部时,
,
故答案为:或.
11.解:∵在中,点D是边的中点,,的面积是2024,
∴,
∵,
∴;
故答案为:506.
12.解:由题意:
∴
又
∴
∵
∴
∴
故答案为:.
13.解:,,
,
平分,
,
,
,
,
,
,
,
.
故答案为:.
14.解:如图,
,,,
.
故答案为:.
15.解:延长,交于点,
而图中
应增加;
故答案为:增加,5.
16.解:结论①,
∵,
∴,
∵,
∴,
∴,故结论①正确;
结论②,
如图所示,设交于点,
在中,,
∵平分,
∴,
∵,
∴,
∴,故结论②错误;
结论③若,,则,
∵,且,
∴,
∴,
∵平分,平分,
∴,
∴,则,
∵,
∴,,
∴,
∴,故结论③正确;
综上所述,正确的有①③,
故答案为:①③ .
17.(1)解:由三角形三边关系定理得:,
.
故答案为:.
(2)解:,,,
.
18.(1)解:不可能,理由如下:
设多边形的边数为n,由题意得:,
解得:
∵多边形的边数n为正整数,
∴多边形的内角和不可能为;
(2)解:∵设应加的内角为x度,多加的外角为y度,多边形的边数为m,
由题意得:,
∵,
∴,
∵m为正整数,
∴m为13或14,
∴宝宝求的是十三边形或十四边形的内角和.
19.(1)解:如图,即为所求;
(2)解:根据平移的性质可得:线段和平行且相等.
故答案为:平行且相等
(3)解:如(1)图,线段,即为所求;
(4)解:.
故答案为:23
20.((1)证明:因为,
所以(两直线平行,内错角相等).
因为(平角的定义).
所以(等量代换),
即三角形的内角和为;
(2)解:∵,
∴,
∵,,
∴,
∴.
21.(1)证明:∵平分,
∴,
∴,
又∵,
∴,
∴;
(2)解:①∵平分,由(1)得,
∴,
又∵,
∴,
又∵平分,
∴,
∴;
②∵,由(1)得,由①得,
∴,
∵,
∴,
∴,
∴,
∴,
∴.
22.解:(1)∵,
∴,
∵,分别是和的平分线,
∴,,
∴,
∴在中,.
(2),,
.
平分,平分,
,.
.
.
(3)平分,平分,
∴,,
∵
∴.
一、单选题
1.已知一个三角形的三边长分别为2、4、x,那么的取值可以是( )
A.1 B.2 C.4 D.7
2.如图,把手机放在一个支架上面,就可以非常方便地使用,这种方法应用的几何原理是( )
A.三角形的稳定性 B.两点之间线段最短
C.两点确定一条直线 D.垂线段最短
3.将沿方向平移得到.若,,则的度数是( )
A. B. C. D.
4.如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )
A.6 B.7 C.8 D.9
5.只用下列四种正多边形中的一种,不能铺满地面的是( )
A. B. C. D.
6.如图,在中,是高,是角平分线,是中线,则下列说法中错误的是( )
A. B.
C. D.
7.如图,为的中线,为的中线.若的面积为10,则的面积为( )
A.40 B.30 C.20 D.15
8.五边形的边所在直线形成如图所示的形状,则( )
A. B. C. D.
二、填空题
9.如图,E是边的中点,若,的周长比的周长多1,则 .
10.已知中,为边上的高,,则 .
11.如图,在中,点D是边的中点,点E是边上一点,和交于点O,,的面积是2024,若把的面积记为,把四边形的面积记为,则的值为 .
12.将一个正五边形和一个正六边形按如图所示的方式放在直线上,连接正五边形的对角线,则的度数为 .
13.如图,中,,,平分,于D,,则的度数 .
14.如图,的度数是 .
15.如图是可调躺椅示意图(数据如图),与的交点为,且,,保持不变.为了舒适,可调整的大小,使,则图中应 (填“增加”或“减少”) 度.
16.如图,,,延长至点,连接,和的角平分线交于点,下列三个结论:①;②;③若,,则.其中结论正确的个数有 .
三、解答题
17.已知a、b、c是一个三角形的三边长.
(1)若,,则c的取值范围是_______.
(2)试化简:.
18.根据下列对话,回答问题:
宝宝:我把一个多边形的各内角相加,所得的和为;
贝贝:什么?不可能的!你错把一个外角当作内角了!
(1)多边形的内角和为,为什么不可能?
(2)宝宝求的是几边形的内角和?
19.如图,方格纸中每个小正方形边长均为1,在方格纸内将的点C平移至点得到.
(1)画出;
(2)线段和的关系是_______.
(3)借助方格画出边上的中线和高;
(4)四边形 面积为_______.
20.【探究学习】小学阶段,我们可以通过“拼”角、“折”角,观察得到三角形内角和为 ,现在我们学行线的性质,就可以证明此结论的正确性了.
(1)如图1,过 的顶点作的平行线,请你证明三角形的内角和为
证明:因为,
所以 ( ).
因为( ).
所以 (等量代换),
即三角形的内角和为.
【解题反思】
平行线具有“等角转化”的功能.
【迁移应用】
(2)近年来,我国一直提倡“绿色环保、低碳生活”,健康骑行越来越受到老百姓的喜欢.自行车的示意图如图2,其中.若,,则的度数为 .
21.如图,在中,平分交于点,点为直线上一点,连接,,连接交于点,作平分交于点.
(1)求证:;
(2)若.
①试判断,,之间的数量关系,并说明理由;
②若,求的度数.
22.(1)如图1,在中,,,的平分线相交于点P,求;
(2)如图2,在中,,的外角,的平分线相交于点P,求;
(3)如图3,的的平分线与其外角的平分线相交于点P,若,求的度数.(用含的代数式表示)
参考答案
1.解:由三角形三边关系定理得,
解得:,
四个选项中符合题意的只有4.
故选:C.
2.解:把手机放在一个支架上面,手机和支架形成了一个三角形,
因此这里所用的几何原理是:三角形的稳定性,
故选A.
3.解:根据题意,由平移的性质得:,
∴,
故选:B .
4.解:多边形的外角和是,根据题意得:
解得.
故选C.
5.解:A、正三角形的每个内角的度数为,且,则能铺满地面,此项不符题意;
B、正四边形的每个内角的度数为,且,则能铺满地面,此项不符题意;
C、正六边形的每个内角的度数为,且,则能铺满地面,此项不符题意;
D、正九边形的每个内角的度数为,且,则不能铺满地面,此项符题意;
故选:D.
6.解:∵是的中线,
,A说法正确,不符合题意;
是高,
,
,B说法正确,不符合题意;
是角平分线,
,而与不一定相等,C说法错误,符合题意;
,
,D说法正确,不符合题意;
故选:C.
7.解:∵为的中线.的面积为10,
∴,
∵为的中线,
∴,
故选:A.
8.解:如图所示,
∵,,
又∵,
∴.
故选:C.
9.解:E是边的中点,
,
的周长比的周长多1,且,
,
即,
,
故答案为:5.
10.解:①如图,当在的内部时,
,
②如图,当在的外部时,
,
故答案为:或.
11.解:∵在中,点D是边的中点,,的面积是2024,
∴,
∵,
∴;
故答案为:506.
12.解:由题意:
∴
又
∴
∵
∴
∴
故答案为:.
13.解:,,
,
平分,
,
,
,
,
,
,
,
.
故答案为:.
14.解:如图,
,,,
.
故答案为:.
15.解:延长,交于点,
而图中
应增加;
故答案为:增加,5.
16.解:结论①,
∵,
∴,
∵,
∴,
∴,故结论①正确;
结论②,
如图所示,设交于点,
在中,,
∵平分,
∴,
∵,
∴,
∴,故结论②错误;
结论③若,,则,
∵,且,
∴,
∴,
∵平分,平分,
∴,
∴,则,
∵,
∴,,
∴,
∴,故结论③正确;
综上所述,正确的有①③,
故答案为:①③ .
17.(1)解:由三角形三边关系定理得:,
.
故答案为:.
(2)解:,,,
.
18.(1)解:不可能,理由如下:
设多边形的边数为n,由题意得:,
解得:
∵多边形的边数n为正整数,
∴多边形的内角和不可能为;
(2)解:∵设应加的内角为x度,多加的外角为y度,多边形的边数为m,
由题意得:,
∵,
∴,
∵m为正整数,
∴m为13或14,
∴宝宝求的是十三边形或十四边形的内角和.
19.(1)解:如图,即为所求;
(2)解:根据平移的性质可得:线段和平行且相等.
故答案为:平行且相等
(3)解:如(1)图,线段,即为所求;
(4)解:.
故答案为:23
20.((1)证明:因为,
所以(两直线平行,内错角相等).
因为(平角的定义).
所以(等量代换),
即三角形的内角和为;
(2)解:∵,
∴,
∵,,
∴,
∴.
21.(1)证明:∵平分,
∴,
∴,
又∵,
∴,
∴;
(2)解:①∵平分,由(1)得,
∴,
又∵,
∴,
又∵平分,
∴,
∴;
②∵,由(1)得,由①得,
∴,
∵,
∴,
∴,
∴,
∴,
∴.
22.解:(1)∵,
∴,
∵,分别是和的平分线,
∴,,
∴,
∴在中,.
(2),,
.
平分,平分,
,.
.
.
(3)平分,平分,
∴,,
∵
∴.
