6.2.4 向量的数量积 课件(共26张PPT)
文档属性
| 名称 | 6.2.4 向量的数量积 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 544.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-25 12:39:18 | ||
图片预览






文档简介
(共26张PPT)
平面向量的运算
6.2.4 向量的数量积(1)
第六章
1.了解向量数量积的物理背景,即物体在力F 的作用下产生位移s所做的功.
2.掌握向量数量积的定义及投影向量.
3.会计算平面向量的数量积.
核心素养:数学抽象、逻辑推理、数学运算、直观想象
学习目标
高中数学 必修第二册 RJ ·A
高中数学 必修第二册 RJ ·A
① 新知学习
知识点一两向量的夹角与垂直
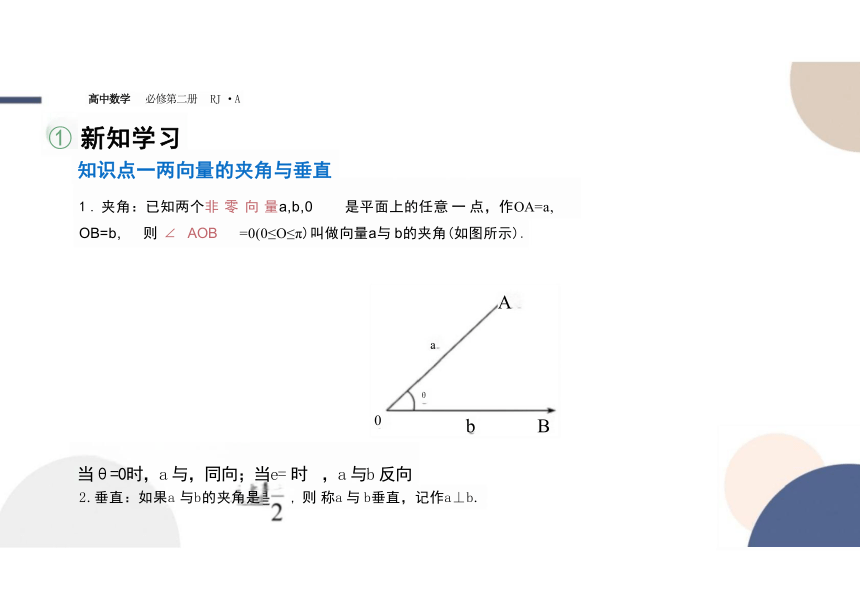
1 . 夹角:已知两个非 零 向 量a,b,0 是平面上的任意 一 点,作OA=a, OB=b, 则 ∠ AOB =0(0≤O≤π)叫做向量a与 b的夹角(如图所示).
当θ=0时,a 与,同向;当e= 时 ,a 与b 反向
2.垂直:如果a 与b的夹角是 , 则 称a 与 b垂直,记作a⊥b.
A
b B
a
θ 0
高中数学 必修第二册 RJ ·A
知识点二向量数量积的定义
已知两个非零向量a,b, 它们的夹角为θ,我们把数量_alblcosθ叫做向量a与b的数量积(或内积),记作 a-b,即 a-b=la|blcos θ.
规定:零向量与任一向量的数量积为
思考 若a≠0, 且a-b=0, 是否能推出b=0
答案 在实数中,若a≠0,且 a-b=0, 则b=0; 但是在数量积中,若a≠0,且 a-b=0, 不能推出b=0. 因为其
中a有可能垂直于b.
高中数学 必修第二册 RJ ·A
知识点三投影向量
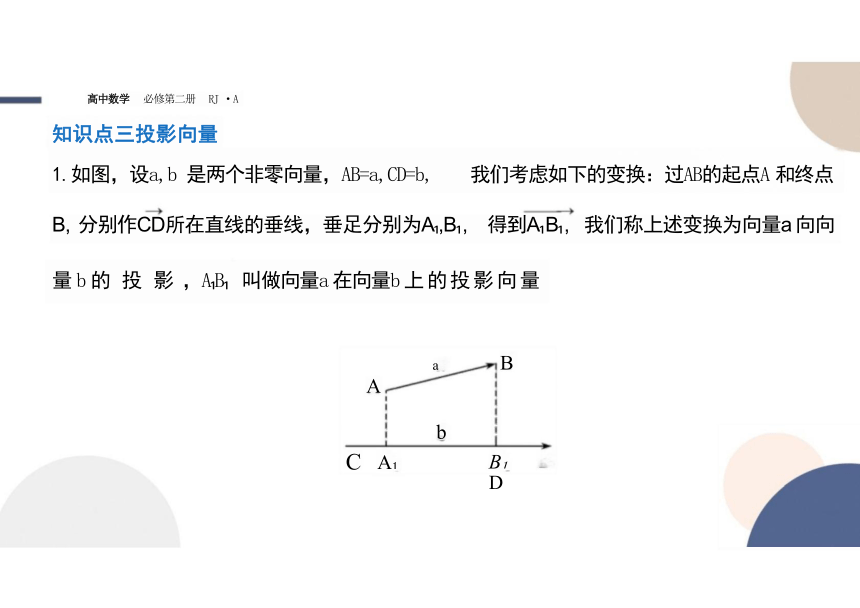
1.如图,设a,b 是两个非零向量,AB=a,CD=b, 我们考虑如下的变换:过AB的起点A 和终点
B, 分别作CD所在直线的垂线,垂足分别为A ,B , 得到A B , 我们称上述变换为向量a 向向 量 b 的 投 影 ,A B 叫做向量a 在向量b 上的投影向量
a B
A
b
C A
B D
高中数学 必修第二册 RJ ·A
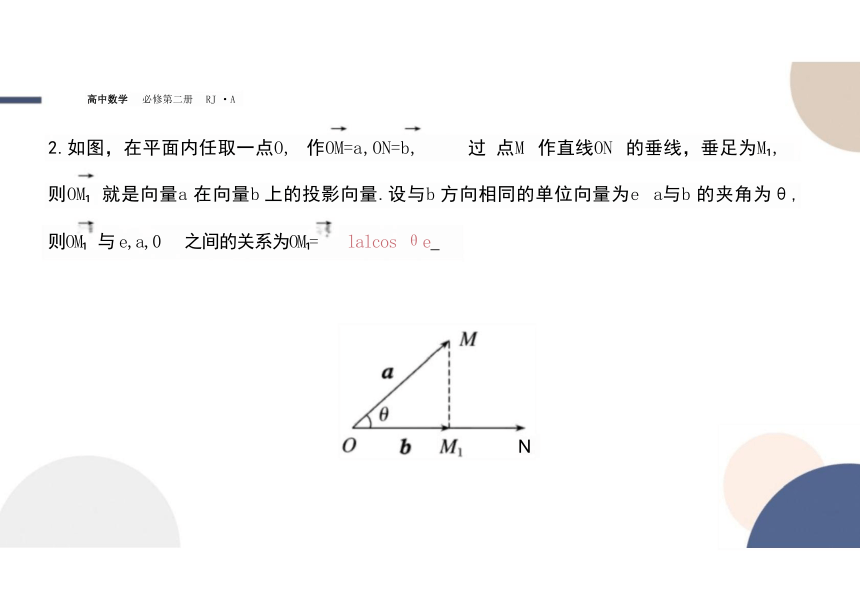
2.如图,在平面内任取一点O, 作OM=a,ON=b, 过 点M 作直线ON 的垂线,垂足为M ,
则OM 就是向量a 在向量b 上的投影向量.设与b 方向相同的单位向量为e a与b 的夹角为θ, 则OM 与 e,a,0 之间的关系为OM = lalcos θe_
N
高中数学 必修第二册 RJ ·A
知识点四平面向量数量积的性质
设向量a与b都是非零向量,它们的夹角为θ,e是与b方向相同的单位向量.则
(1)a-e=e·a=|a|cosθ .
(2)alb a·b
(3)当a//b时
特别地,aa= lal 或a|=o
(4)|a-b| ≤ _lallb|.
高中数学 必修第二册 RJ ·A
易错辨析
1.两个向量的数量积是一个向量. (× )
2.向量a在向量b上的投影向量一定与b共线. ( √ ) 3.若a ·b<0,则a与b的夹角为钝角. (× )
4.若a≠0,则对任一非零向量b都有a·b≠0.(
例1 已知|a|=|b|=2, 且a与b的夹角为60°,则a+b 与a的夹角是多少 a-b 与a的夹角又是多少
高中数学 必修第二册 RJ ·A
典例剖析
一、向量的夹角
高中数学 必修第二册 RJ ·A
解 如图所示,作OA=a,OB=b, 且∠AOB=60°.
以OA,O B为邻边作平行四边形OACB,
则OC=a+b,BA=a-b.
因为|a|=|b|=2, 所以平行四边形0ACB是菱形,又∠AOB=60°,
所以OC 与OA 的夹角为30°,BA 与OA 的夹角为60°.
即a+b 与a的夹角是30°,a-b 与a的夹角是60°.
求两个向量夹角的关键是利用平移的方法使两个向量起点重合,作两个向量的夹角,按照“一
作二证三算”的步骤求出.
反思感悟
高中数学 必修第二册 RJ ·A
跟踪训练
在△ABC中 ,, ∠C=90°, ,则AB 与BC 的夹角是
A.30° B.60°
C.120° D.150°
C 解析 如图,作向量AD=BC,
则∠BAD是AB与BC的夹角,
在△ABC 中,因为∠ACB=90°,
所以∠ABC=60°, 所以∠BAD=120°
高中数学 必修第二册 RJ ·A
高中数学 必修第二册 RJ ·A
二求两向量的数量积
例2 已知正三角形ABC的边长为1,求:(1)AB-AC; 解 ∵AB与AC的夹角为60°,
(2)AB·BC;
→
解 ∵AB 与BC的夹角为120°,
定义法求平面向量的数量积
若已知两向量的模及其夹角,则直接利用公式a-b=|al|b|cos θ.运用此法计算数量积的关键是确定 两个向量的夹角,条件是两向量的起点必须重合,否则,要通过平移使两向量符合以上条件.
反思感悟
高中数学 必修第二册 RJ ·A
在等腰直角三角形ABC中,AB=BC=4,则AB·BC=0 ,BC·CA=-16 ,CA·AB=-16
解析由题意,得AB|=4,IBC|=4,
所以AB·BC=4×4×cos 90°=0,BC·CA=4×4√2×cos 135°=-16,
CA·AB=4√2×4×cos 135°= 16.
跟踪训练
高中数学 必修第二册 RJ ·A
高中数学 必修第二册 RJ ·A
三、投影向量
例3 已知|a|=3,b|=1, 向 量a与向量b的夹角为120°,求a在b上的投影向量. 解 ∵ b|=1,∴b 为单位向量.
∴a在 b 上的投影向量为
投影向量的求法
(1)向量a在向量b上的投影向量为|a|cosθe(其中e为与b同向的单位向量),它是一个向量,且与b共 线,其方向由向量a和b的夹
(2)向量a在向量b上的投影向
反思感悟
高中数学 必修第二册 RJ ·A
已知|a|=12, |b|=8,a-b=24, 求 a在b上的投影向量.
解 ∵a-b=|alb|cosθ,
∴a 在 b 上的投影向量为
跟踪训练
高中数学 必修第二册 RJ ·A
高中数学 必修第二册 RJ ·A
随堂小测
1.已知|a|= √3,b|=2 √3,a与b的夹角是120°,则a·b等于
A.3 B.-3
C.-3√3 D.3√3
B解析由数量积的定义,得
故选B.
高中数学 必修第二册 RJ ·A
2.已知向量|a|=10, |b|=12, 且 a ·b=-60, 则向量a与b的夹角为
A.60° B.120°
C.135° D.150°
B 解析 设a与b的夹角为θ,
又0°≤0≤180°,∴θ=120°
高中数学 必修第二册 RJ ·A
3. (多选)对于任意向量a,b,c, 下列命题中不正确的是
A.若a·b=0, 则a与b中至少有一个为0
B.|a+b|=|a|+|b|
C.若a⊥b, 则a·b=0
D.la|=\a
高中数学 必修第二册 RJ ·A
AB 解析 a ·b=0→a⊥b或a=0 或b=0, 所 以A错误;
根据向量加法的平行四边形法则,知|a+b≤|a|+|b|,只 有 当a,b 同向时取“=”,所以B错误;
由数量积的性质知,C 正确;
因为a·a=|a||a|cos O=|al
所以|a|= √a ,所 以D 正确.
高中数学 必修第二册 RJ ·A
→
4.在等腰直角三角形ABC中,若∠C=90°,AC=√2,则BABC的值等于
A.-2 B.2
C.-2√2 D.2√2 B解析 BABC=|BA[BC|cos ∠ABC=2×√2×cos 45°=2.
高中数学 必修第二册 RJ ·A
5.已知|a|=2,|b|=3, 且 a与b的夹角为60°,与b同向的单位向量为e, 则向量a在向量b上的投影向量为
e
解析 设a与b的夹角为θ ,a 在b上的投影向量为
高中数学 必修第二册 RJ ·A
课堂小结
1.知识清单:
(1)向量的夹角.
(2)向量数量积的定义.
(3)投影向量.
(4)向量数量积的性质. 2.方法归纳:数形结合
3.常见误区:向量夹角共起点;a·b>0≠两向量夹角为锐角,a-b<0≠ 两向量夹角为钝角
高中数学 必修第二册 RJ ·A
平面向量的运算
6.2.4 向量的数量积(1)
第六章
1.了解向量数量积的物理背景,即物体在力F 的作用下产生位移s所做的功.
2.掌握向量数量积的定义及投影向量.
3.会计算平面向量的数量积.
核心素养:数学抽象、逻辑推理、数学运算、直观想象
学习目标
高中数学 必修第二册 RJ ·A
高中数学 必修第二册 RJ ·A
① 新知学习
知识点一两向量的夹角与垂直
1 . 夹角:已知两个非 零 向 量a,b,0 是平面上的任意 一 点,作OA=a, OB=b, 则 ∠ AOB =0(0≤O≤π)叫做向量a与 b的夹角(如图所示).
当θ=0时,a 与,同向;当e= 时 ,a 与b 反向
2.垂直:如果a 与b的夹角是 , 则 称a 与 b垂直,记作a⊥b.
A
b B
a
θ 0
高中数学 必修第二册 RJ ·A
知识点二向量数量积的定义
已知两个非零向量a,b, 它们的夹角为θ,我们把数量_alblcosθ叫做向量a与b的数量积(或内积),记作 a-b,即 a-b=la|blcos θ.
规定:零向量与任一向量的数量积为
思考 若a≠0, 且a-b=0, 是否能推出b=0
答案 在实数中,若a≠0,且 a-b=0, 则b=0; 但是在数量积中,若a≠0,且 a-b=0, 不能推出b=0. 因为其
中a有可能垂直于b.
高中数学 必修第二册 RJ ·A
知识点三投影向量
1.如图,设a,b 是两个非零向量,AB=a,CD=b, 我们考虑如下的变换:过AB的起点A 和终点
B, 分别作CD所在直线的垂线,垂足分别为A ,B , 得到A B , 我们称上述变换为向量a 向向 量 b 的 投 影 ,A B 叫做向量a 在向量b 上的投影向量
a B
A
b
C A
B D
高中数学 必修第二册 RJ ·A
2.如图,在平面内任取一点O, 作OM=a,ON=b, 过 点M 作直线ON 的垂线,垂足为M ,
则OM 就是向量a 在向量b 上的投影向量.设与b 方向相同的单位向量为e a与b 的夹角为θ, 则OM 与 e,a,0 之间的关系为OM = lalcos θe_
N
高中数学 必修第二册 RJ ·A
知识点四平面向量数量积的性质
设向量a与b都是非零向量,它们的夹角为θ,e是与b方向相同的单位向量.则
(1)a-e=e·a=|a|cosθ .
(2)alb a·b
(3)当a//b时
特别地,aa= lal 或a|=o
(4)|a-b| ≤ _lallb|.
高中数学 必修第二册 RJ ·A
易错辨析
1.两个向量的数量积是一个向量. (× )
2.向量a在向量b上的投影向量一定与b共线. ( √ ) 3.若a ·b<0,则a与b的夹角为钝角. (× )
4.若a≠0,则对任一非零向量b都有a·b≠0.(
例1 已知|a|=|b|=2, 且a与b的夹角为60°,则a+b 与a的夹角是多少 a-b 与a的夹角又是多少
高中数学 必修第二册 RJ ·A
典例剖析
一、向量的夹角
高中数学 必修第二册 RJ ·A
解 如图所示,作OA=a,OB=b, 且∠AOB=60°.
以OA,O B为邻边作平行四边形OACB,
则OC=a+b,BA=a-b.
因为|a|=|b|=2, 所以平行四边形0ACB是菱形,又∠AOB=60°,
所以OC 与OA 的夹角为30°,BA 与OA 的夹角为60°.
即a+b 与a的夹角是30°,a-b 与a的夹角是60°.
求两个向量夹角的关键是利用平移的方法使两个向量起点重合,作两个向量的夹角,按照“一
作二证三算”的步骤求出.
反思感悟
高中数学 必修第二册 RJ ·A
跟踪训练
在△ABC中 ,, ∠C=90°, ,则AB 与BC 的夹角是
A.30° B.60°
C.120° D.150°
C 解析 如图,作向量AD=BC,
则∠BAD是AB与BC的夹角,
在△ABC 中,因为∠ACB=90°,
所以∠ABC=60°, 所以∠BAD=120°
高中数学 必修第二册 RJ ·A
高中数学 必修第二册 RJ ·A
二求两向量的数量积
例2 已知正三角形ABC的边长为1,求:(1)AB-AC; 解 ∵AB与AC的夹角为60°,
(2)AB·BC;
→
解 ∵AB 与BC的夹角为120°,
定义法求平面向量的数量积
若已知两向量的模及其夹角,则直接利用公式a-b=|al|b|cos θ.运用此法计算数量积的关键是确定 两个向量的夹角,条件是两向量的起点必须重合,否则,要通过平移使两向量符合以上条件.
反思感悟
高中数学 必修第二册 RJ ·A
在等腰直角三角形ABC中,AB=BC=4,则AB·BC=0 ,BC·CA=-16 ,CA·AB=-16
解析由题意,得AB|=4,IBC|=4,
所以AB·BC=4×4×cos 90°=0,BC·CA=4×4√2×cos 135°=-16,
CA·AB=4√2×4×cos 135°= 16.
跟踪训练
高中数学 必修第二册 RJ ·A
高中数学 必修第二册 RJ ·A
三、投影向量
例3 已知|a|=3,b|=1, 向 量a与向量b的夹角为120°,求a在b上的投影向量. 解 ∵ b|=1,∴b 为单位向量.
∴a在 b 上的投影向量为
投影向量的求法
(1)向量a在向量b上的投影向量为|a|cosθe(其中e为与b同向的单位向量),它是一个向量,且与b共 线,其方向由向量a和b的夹
(2)向量a在向量b上的投影向
反思感悟
高中数学 必修第二册 RJ ·A
已知|a|=12, |b|=8,a-b=24, 求 a在b上的投影向量.
解 ∵a-b=|alb|cosθ,
∴a 在 b 上的投影向量为
跟踪训练
高中数学 必修第二册 RJ ·A
高中数学 必修第二册 RJ ·A
随堂小测
1.已知|a|= √3,b|=2 √3,a与b的夹角是120°,则a·b等于
A.3 B.-3
C.-3√3 D.3√3
B解析由数量积的定义,得
故选B.
高中数学 必修第二册 RJ ·A
2.已知向量|a|=10, |b|=12, 且 a ·b=-60, 则向量a与b的夹角为
A.60° B.120°
C.135° D.150°
B 解析 设a与b的夹角为θ,
又0°≤0≤180°,∴θ=120°
高中数学 必修第二册 RJ ·A
3. (多选)对于任意向量a,b,c, 下列命题中不正确的是
A.若a·b=0, 则a与b中至少有一个为0
B.|a+b|=|a|+|b|
C.若a⊥b, 则a·b=0
D.la|=\a
高中数学 必修第二册 RJ ·A
AB 解析 a ·b=0→a⊥b或a=0 或b=0, 所 以A错误;
根据向量加法的平行四边形法则,知|a+b≤|a|+|b|,只 有 当a,b 同向时取“=”,所以B错误;
由数量积的性质知,C 正确;
因为a·a=|a||a|cos O=|al
所以|a|= √a ,所 以D 正确.
高中数学 必修第二册 RJ ·A
→
4.在等腰直角三角形ABC中,若∠C=90°,AC=√2,则BABC的值等于
A.-2 B.2
C.-2√2 D.2√2 B解析 BABC=|BA[BC|cos ∠ABC=2×√2×cos 45°=2.
高中数学 必修第二册 RJ ·A
5.已知|a|=2,|b|=3, 且 a与b的夹角为60°,与b同向的单位向量为e, 则向量a在向量b上的投影向量为
e
解析 设a与b的夹角为θ ,a 在b上的投影向量为
高中数学 必修第二册 RJ ·A
课堂小结
1.知识清单:
(1)向量的夹角.
(2)向量数量积的定义.
(3)投影向量.
(4)向量数量积的性质. 2.方法归纳:数形结合
3.常见误区:向量夹角共起点;a·b>0≠两向量夹角为锐角,a-b<0≠ 两向量夹角为钝角
高中数学 必修第二册 RJ ·A
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
