人教A版高一数学《6.2平面向量的运算—加法 减法》 课件(共29张PPT)
文档属性
| 名称 | 人教A版高一数学《6.2平面向量的运算—加法 减法》 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-25 12:37:36 | ||
图片预览







文档简介
(共29张PPT)
6.2平面向量的运算—加法 减法
以前,乘车从慈溪去嘉兴要先从慈溪到杭州再由杭州到嘉兴,则两次位移的总效 果如何
苏州
上海 东海
洋山港
杭州湾跨海大桥
杭州湾新区
慈溪 慈溪
东方上海
嘉兴
杭州
北仑港
宁波
第1页/共29页
sh,eastda
勇杭高速公
AB+BC=AC
问 :
临港 AB BC
第2页/共29页
AC
(1)在平面内任取一点A
(2)作AB=a,BC=b
(3)则向量AC=a+b
a+b=AB+BC=AC
向量的加法
定义:求两个向量和的运算,叫做向量的加法.
向量加法的三角形法则
作法:
B
作平移,首尾相连,由起点指向终点.
注意:两个向量的和仍然是一个向量
首 尾 相 连
第3页/共29页
Q
十
第4页/共29页
首 尾 相 连
Q 十
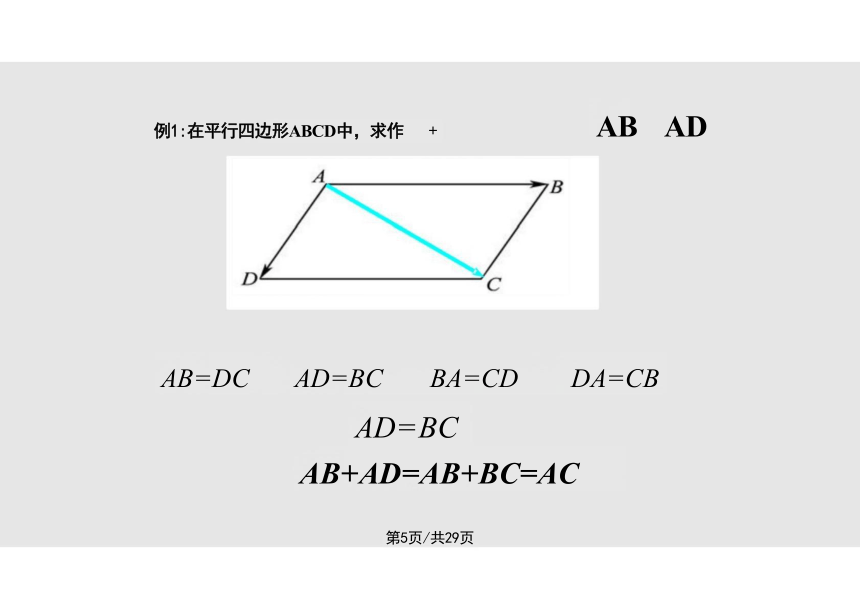
AB=DC AD=BC BA=CD DA=CB
AD=BC
AB+AD=AB+BC=AC
第5页/共29页
例1:在平行四边形ABCD中,求作 + AB AD
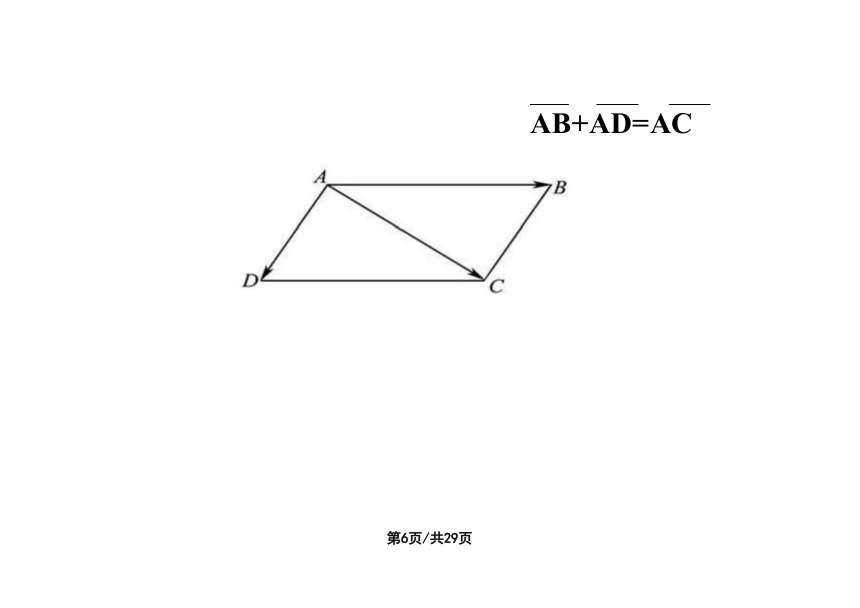
AB+AD=AC
第6页/共29页
作平移,共起点,四边形,对角线
第7页/共29页
向量加法的平行四边形法则
AB+AL
B
AB+AD A
首 首 相 连
D C
A
作 法:(1)在平面内任取 一 点A
(2)作 AB=a,AD=b
(3)以AB,AD 为邻边作平行四边形
ABCD
则
AC=a+b
向量的加法
b
a
第8页/共29页
练一练
如图,已知 用向量加法的平行四边形法则作出
a+b
a
a+b a
b
b
a
首 首 相 连
(1)
(2)
第9页/共29页
●
二
向量的加法交换律
问: 不移动向量,而移动向 量 结果是否和原来一样呢
AB
AB+AD=AC
第10页/共29页
D C
(1)AB+BC
(2)AB+AD
(3)AD+CD A B 解 : (1)AB+BC=AC
(2)AB+AD=AC
(3)因为 AD =BC 所以 AD+CD=BC+CD=BD
即
AD+CD=BD
第12页/共29页
1.向量加法的三角形法则
(要点:前尾相建前尾连)
2.向量加法的平行四边形法则
(要点:起点重合,同起点的对角线
3.向量加法满足交换律
a+b=b+a
小结与回顾
第13页/共29页
创设情境
热身运动:拔河
第14页/共29页
创设情境
热身运动:拔河
第15页/共29页
提出课题
1、相反向量:与非零向量a 长度相等,且方向相
反的向量叫做向量a 的相反向量,记作 。-a
说明: ① 规定 -0=0
②性质 -(-a)=ā
a+(-a)=(-a)+a=0
第16页/共29页
与向量 的差,即
求两个向量差的运算叫作向量的减法
提出课题
2、向量的减法:
的负向量的和定义为向量
向量
a
第17页/共29页
与向量
b
a
=OA+BO=BO+OA=BA
作法:在平面内任取一点O, 作
, 则
OA=a OB
1、向量减法法则:已知向量 ,
C=a-b
共同探究
向 量 , 使
C
,求作
第18页/共29页
共同探究
向量减法法则
OA-OB=BA
归纳概括: (1)将两向量移到共同起点
(2)连接两向量的终点,
(3)方向指向被减向量
同起点,连终点,指向被减
第19页/共29页
共同探究
2、小试牛刀
已知向量和 (如下图)b 请分别画出
和
a-b -a
第20页/共29页
共同探究
3、动脑思考
a b若、共线时,怎样作 a-b
①共线同向 ②共线反向
a-b=AB-AC=CB
第21页/共29页
应用举例
例 1 已知如图所示向量 a ,请画出向量 a-b
第22页/共29页
应用举例
例2化简:
(2)OD-OA (2)AB-AC+BD+DC 解:(1) OD-OA=AD
(2)AB-AC+BD+DC
=CB+BD+DC
=CD+DC
=CC=0
第23页/共29页
学以致用
求作 a-b
第24页/共29页
1、已知
学以致用
2、快速抢答:
AB-AD= DB OB-OC-DB= CD
OA+0C+BO+CO=_ BA
AB-AC+BD+DC= 0
AB+BC-DC+DA=0
BA-BC= CA
OA-OB= BA
NQ+QP+MN-MP= 0
AB+BC-AD-DB=BC MD+MN-MP+DP= MN
第25页/共29页
备选题:
如图所示,在平行四边形ABCD 中,设
AB=a ,表示向量 a`b
BD DB
D
用
A
试
第26页/共29页
AC
课堂小结
1、向量减法的定义及其几何意义
2、正确熟练地掌握向量减法法则:
共起点、连终点、指向被减
第27页/共29页
作业:
· 教材P89, 课堂练习第1、2题
第28页/共29页
感谢您的观看。
第29页/共29页
6.2平面向量的运算—加法 减法
以前,乘车从慈溪去嘉兴要先从慈溪到杭州再由杭州到嘉兴,则两次位移的总效 果如何
苏州
上海 东海
洋山港
杭州湾跨海大桥
杭州湾新区
慈溪 慈溪
东方上海
嘉兴
杭州
北仑港
宁波
第1页/共29页
sh,eastda
勇杭高速公
AB+BC=AC
问 :
临港 AB BC
第2页/共29页
AC
(1)在平面内任取一点A
(2)作AB=a,BC=b
(3)则向量AC=a+b
a+b=AB+BC=AC
向量的加法
定义:求两个向量和的运算,叫做向量的加法.
向量加法的三角形法则
作法:
B
作平移,首尾相连,由起点指向终点.
注意:两个向量的和仍然是一个向量
首 尾 相 连
第3页/共29页
Q
十
第4页/共29页
首 尾 相 连
Q 十
AB=DC AD=BC BA=CD DA=CB
AD=BC
AB+AD=AB+BC=AC
第5页/共29页
例1:在平行四边形ABCD中,求作 + AB AD
AB+AD=AC
第6页/共29页
作平移,共起点,四边形,对角线
第7页/共29页
向量加法的平行四边形法则
AB+AL
B
AB+AD A
首 首 相 连
D C
A
作 法:(1)在平面内任取 一 点A
(2)作 AB=a,AD=b
(3)以AB,AD 为邻边作平行四边形
ABCD
则
AC=a+b
向量的加法
b
a
第8页/共29页
练一练
如图,已知 用向量加法的平行四边形法则作出
a+b
a
a+b a
b
b
a
首 首 相 连
(1)
(2)
第9页/共29页
●
二
向量的加法交换律
问: 不移动向量,而移动向 量 结果是否和原来一样呢
AB
AB+AD=AC
第10页/共29页
D C
(1)AB+BC
(2)AB+AD
(3)AD+CD A B 解 : (1)AB+BC=AC
(2)AB+AD=AC
(3)因为 AD =BC 所以 AD+CD=BC+CD=BD
即
AD+CD=BD
第12页/共29页
1.向量加法的三角形法则
(要点:前尾相建前尾连)
2.向量加法的平行四边形法则
(要点:起点重合,同起点的对角线
3.向量加法满足交换律
a+b=b+a
小结与回顾
第13页/共29页
创设情境
热身运动:拔河
第14页/共29页
创设情境
热身运动:拔河
第15页/共29页
提出课题
1、相反向量:与非零向量a 长度相等,且方向相
反的向量叫做向量a 的相反向量,记作 。-a
说明: ① 规定 -0=0
②性质 -(-a)=ā
a+(-a)=(-a)+a=0
第16页/共29页
与向量 的差,即
求两个向量差的运算叫作向量的减法
提出课题
2、向量的减法:
的负向量的和定义为向量
向量
a
第17页/共29页
与向量
b
a
=OA+BO=BO+OA=BA
作法:在平面内任取一点O, 作
, 则
OA=a OB
1、向量减法法则:已知向量 ,
C=a-b
共同探究
向 量 , 使
C
,求作
第18页/共29页
共同探究
向量减法法则
OA-OB=BA
归纳概括: (1)将两向量移到共同起点
(2)连接两向量的终点,
(3)方向指向被减向量
同起点,连终点,指向被减
第19页/共29页
共同探究
2、小试牛刀
已知向量和 (如下图)b 请分别画出
和
a-b -a
第20页/共29页
共同探究
3、动脑思考
a b若、共线时,怎样作 a-b
①共线同向 ②共线反向
a-b=AB-AC=CB
第21页/共29页
应用举例
例 1 已知如图所示向量 a ,请画出向量 a-b
第22页/共29页
应用举例
例2化简:
(2)OD-OA (2)AB-AC+BD+DC 解:(1) OD-OA=AD
(2)AB-AC+BD+DC
=CB+BD+DC
=CD+DC
=CC=0
第23页/共29页
学以致用
求作 a-b
第24页/共29页
1、已知
学以致用
2、快速抢答:
AB-AD= DB OB-OC-DB= CD
OA+0C+BO+CO=_ BA
AB-AC+BD+DC= 0
AB+BC-DC+DA=0
BA-BC= CA
OA-OB= BA
NQ+QP+MN-MP= 0
AB+BC-AD-DB=BC MD+MN-MP+DP= MN
第25页/共29页
备选题:
如图所示,在平行四边形ABCD 中,设
AB=a ,表示向量 a`b
BD DB
D
用
A
试
第26页/共29页
AC
课堂小结
1、向量减法的定义及其几何意义
2、正确熟练地掌握向量减法法则:
共起点、连终点、指向被减
第27页/共29页
作业:
· 教材P89, 课堂练习第1、2题
第28页/共29页
感谢您的观看。
第29页/共29页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
